軌道交通車輛模態參數辨識方法研究*
程 暢
(常州輕工職業技術學院,213164,常州∥副教授)
軌道交通車輛運行平穩性是車輛動力學性能的重要評價指標。模態參數是軌道交通車輛的固有參數,反映振動系統的固有動態特性[1],由懸掛系統的剛度及阻尼,以及部件的慣量及其在系統中的位置共同確定。車輛一旦設計制造完畢,其動力學性能就基本確定。真實車輛的模態參數可在試驗臺或運行工況下通過試驗設計及振動測試,并采用相應的辨識算法通過辨識得出[2]。由于模態參數不依賴于線路輸入條件,而試驗測試得到的模態參數反映了真實車輛包括組裝性能在內的系統動態特性,故通過運用模態參數來評價軌道交通車輛的動態設計性能更具有普遍性。
軌道車輛動力學系統的模態在1 Hz附近較密集,運用傳統辨識算法及工況模態辨識算法計算量較大,并且即使在已知輸入的實驗室條件下,也不能有效辨識這些密集且大阻尼比的模態參數。
子空間辨識數值算法(N4SID)是利用新增輸入輸出數據對在線估計系統參數矩陣進行的一種辨識算法。N4SID不關心被辨識系統的模型結構形態,僅需給定模型的階數(該階數可在辨識過程中觀察矩陣的奇異值獲得),無需求解復雜非線性優化函數,采用奇異值分解(SVD)和正交三角(QR)分解的線性代數算法,避免了疊代算法中收斂、局部最小及初始條件敏感等問題,從而廣泛應用于辨識領域[3]。
本文主要研究運用N4SID算法通過辨識直接獲得系統的狀態方程,通過對系統矩陣進行特征值分解獲得模態參數,然后運用穩態圖來保留真實系統的物理極點,運用所編制的程序對仿真模型進行辨識分析。
1N4SID
N4SID一般包含3個步驟[4]:①運用SVD和QR分解對輸入輸出數據Hankel矩陣進行投影運算,得到投影矩陣Oi,同時確定系統的階次n;②估計求解出拓展可觀測矩陣Γi、或者卡爾曼濾波狀態序列估計i;③確定系統的參數矩陣A、B、C、D。
當m階輸入、l階輸出的n階系統矩陣為線性時,不變系統的離散狀態空間模型可表示為
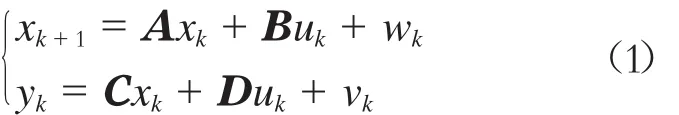
式中:
k——采樣時刻;
A——系統狀態矩陣,為n階方陣;
B——輸入分配矩陣,為n×m矩陣;
C——輸出矩陣,為l×n矩陣;
D——直接輸出矩陣,為l×m矩陣;
vk——測量噪聲,vk∈Rl;
wk——過程噪聲,wk∈Rn。
當輸入未知時,可假設確定性輸入為0,此時系統狀態空間模型不包含B、D矩陣,模型退化為隨機子空間模型。定義輸入數據的Hankel矩陣為

式中:
i——矩陣行數的1/2;
j——矩陣列數,Hankel矩陣U0|2i-1中,i=j;
Up——過去輸入矩陣,是U0|2i-1的分塊矩陣;
Uf——將來輸入矩陣,是U0|2i-1的分塊矩陣。
n×j階狀態序列Xi為


依據以上定義,對
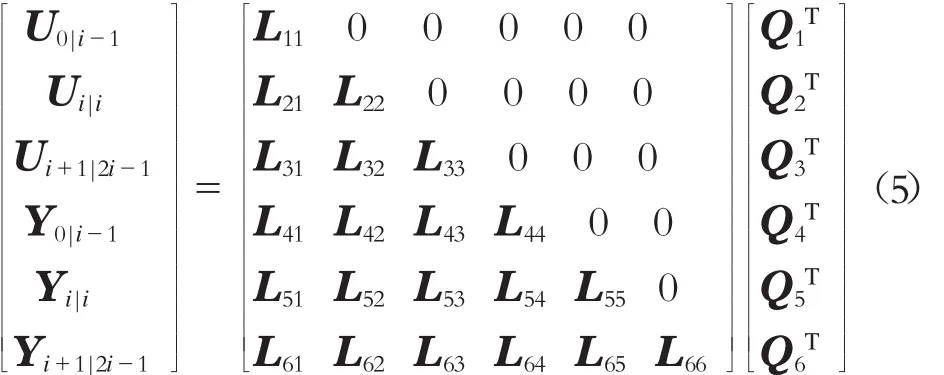
式中:
Ya|b——第1列第1個元素為a,且第1列最后1個元素為b的分塊矩陣。
于是,由“將來”輸入行空間到“過去”輸出行空間的投影矩陣為
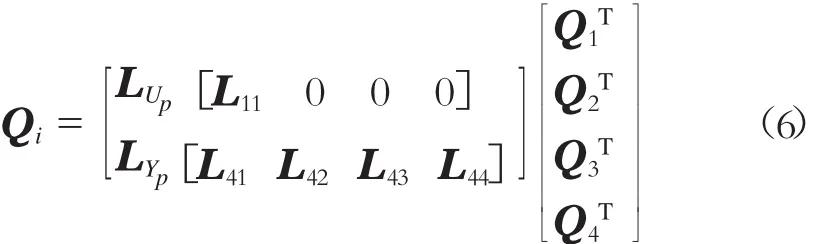
其中
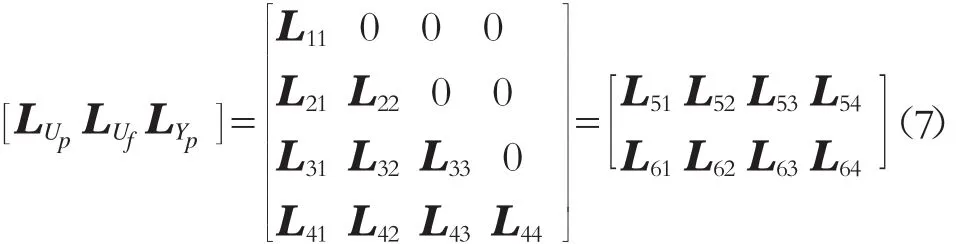
式中:
LUp——L矩陣的過去輸入矩陣;
LUf——L矩陣的將來輸入矩陣;
LYp——L矩陣的過去輸出矩陣。
由式(7)可以求出 LUp、LUf和 LYp。
依據假設條件可知
Qi= Γii(8)
式中:
i——卡爾曼濾波狀態序列Xi的估計。
對式(6)右側第1項進行奇異值分解,依據奇異值分布設定系統的階數,然后對奇異值矩陣進行分
塊為S1和S2的直和,其形式如下。

式中,ρw、ρv為殘差矩陣。
2 車輛模態參數的辨識及分析
由于車輛力學模型的模態參數可通過理論分析準確獲得,所以采用仿真模型不僅可驗證辨識算法的有效性,還可方便地模擬量測噪聲信號,以便于分析噪聲信號對辨識精度的影響[5]。本文運用軌道交通車輛的6自由度垂向動力學模型來校驗算法及所編制辨識程序的有效性。該6自由度車輛的垂向動力學模型如圖1所示。
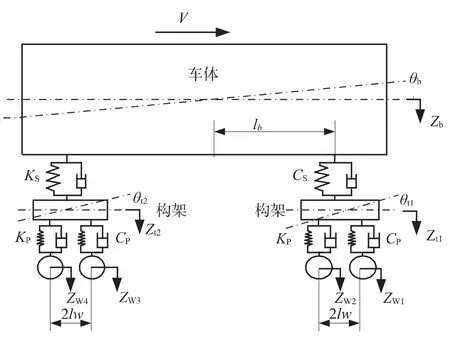
圖1 客車垂向動力學模型圖
根據圖1模型,結合上述子空間辨識算法理論,運用影響系數法建立動力學方程,選取狀態矢量,將動力學方程轉為狀態方程,依據采樣時間對連續系統的狀態方程離散,即可獲得形如式(1)的狀態空間模型。在Simulink/Matlab軟件環境下建立仿真模型如圖2所示。
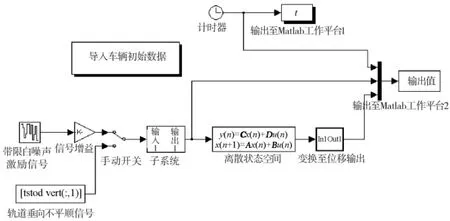
圖2 車輛自由度數為6的垂向Simulink模型圖
在辨識算法研究中,客車動力學模型參數選自某典型客車,離散模型的時間步長為0.005 s(采樣頻率為200 Hz)。本文分別運用帶限白噪聲信號、軌道譜反演的軌道不平順信號及確定性的掃頻信號作為軌道的垂向不平順輸入,并考慮了輪軸輸入的時延,以車體中部、心盤處,以及每個構架的中部、端部共9個測點處的垂向位移作為系統的輸出,對所編制的程序進行了校驗。辨識結果表明,當運用不包含噪聲信號的仿真數據進行辨識時,在各種輸入信號下,均能獲得與理論模態基本一致的高精度辨識結果。
為了分析噪聲對辨識精度的影響,當輸入為白噪聲信號時,在輸出信號上疊加了均方根值為原信號1%和5%的零均值、正態分布噪聲信號(以下分別簡為“1%噪聲”及“5%噪聲”)得到辨識結果如表1所示。辨識結果表明:N4SID算法辨識精度極高,但噪聲信號越強,辨識精度越低。若想提高辨識精度,必須增加所采用的輸出數據點數,但計算時間隨之增加。表1中在5%噪聲信號下的分析結果運用了35 s長的輸出數據才能得到與在1%噪聲信號下、15 s長數據相當的辨識精度。
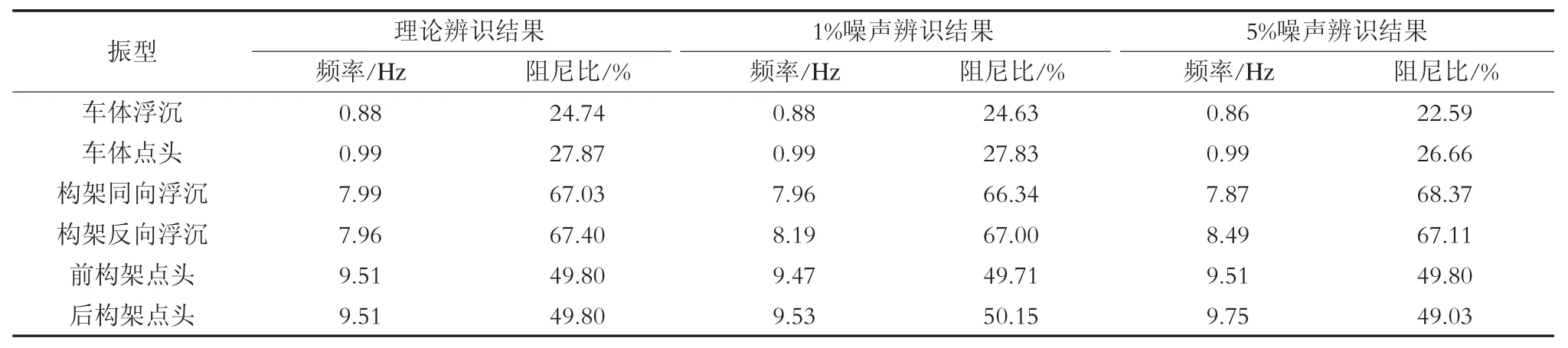
表1 車輛模態參數N4SID算法辨識結果
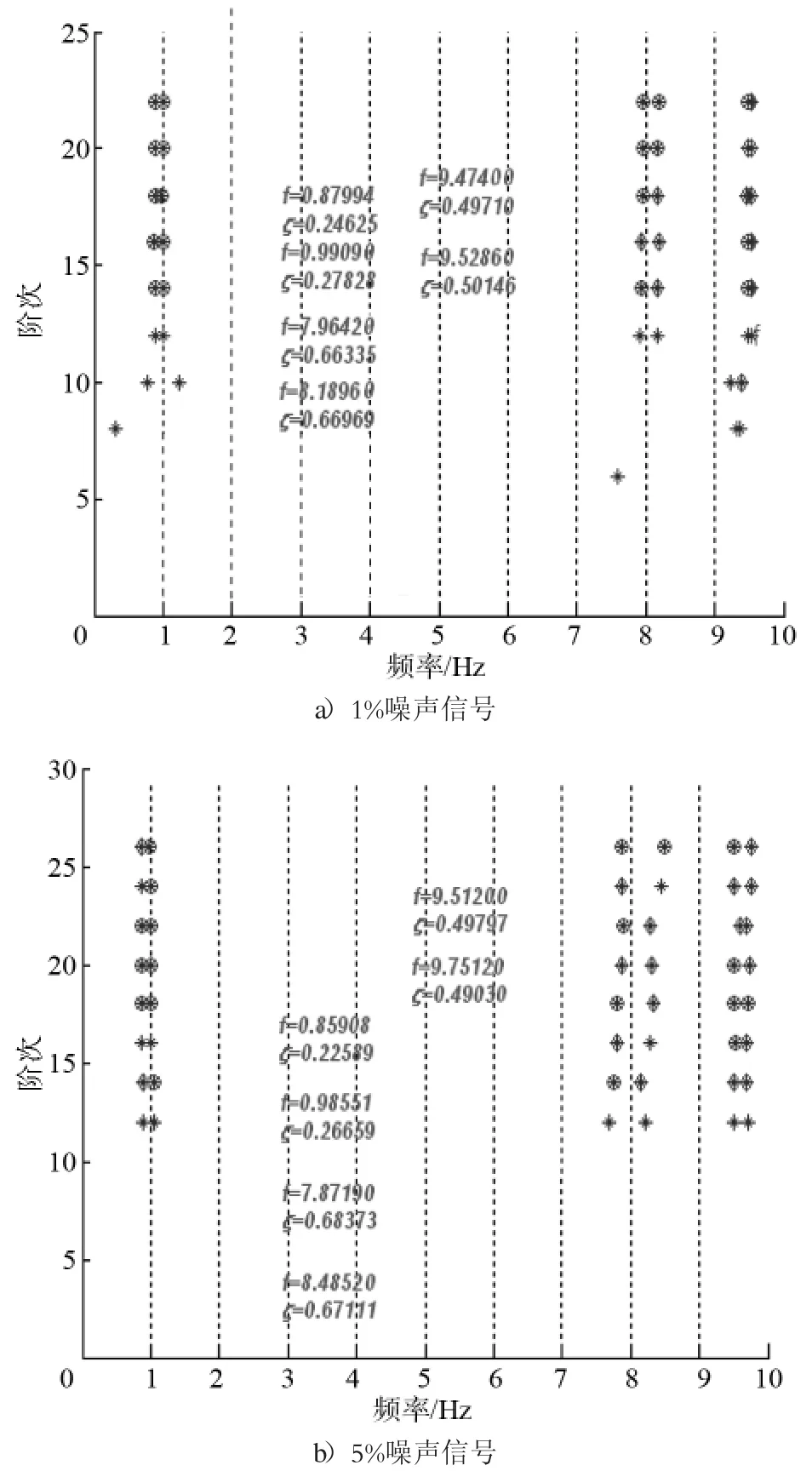
圖3 N4SID的穩態圖
圖3為車輛存在1%噪聲和5%噪聲信號時,為了挑選穩定的系統極點所繪制的穩態圖。繪制穩態圖的準則是特征頻率的變化率不大于1%、阻尼比不大于8%、振型矢量不大于2%。圖3表明:在1%噪聲信號辨識時,較早獲得穩定的極點,并且識別的精度較高。
在實驗室條件下,雖然構架和車體的位移響應可通過測量獲得,但是位移的測量往往比加速度的測量復雜很多。經分析,從軌道不平順至車輛位移及加速度響應的狀態方程中可知,A、B矩陣完全相同,C、D矩陣不同。因此將加速度響應作為系統輸出,如能辨識出系統矩陣A,將獲得位移輸出相同的系統極點,并具有相同的振型頻率和阻尼比。本文運用構架及車體仿真加速度輸出信號進行辨識時發現:當輸出信號沒有噪聲時,仍可精確地辨識出車輛系統的模態參數;但將上述1%噪聲信號及5%噪聲信號加入后,無論是隨機輸入信號、軌道譜反演信號還是掃頻信號都無法獲得良好的辨識效果。在6級軌道譜反演數據輸入時,沒有噪聲和有1%噪聲信號情況下的辨識結果見表2。
從表2可以看出:沒有噪聲信號時,辨識結果基本與理論模態精確一致;有1%噪聲信號時,雖然辨識結果也具有較高精度,但未能辨識車體的點頭振型;當有5%噪聲信號時,只能辨識出構架的點頭振型,而不能有效地辨識車輛的點頭及浮沉振型。
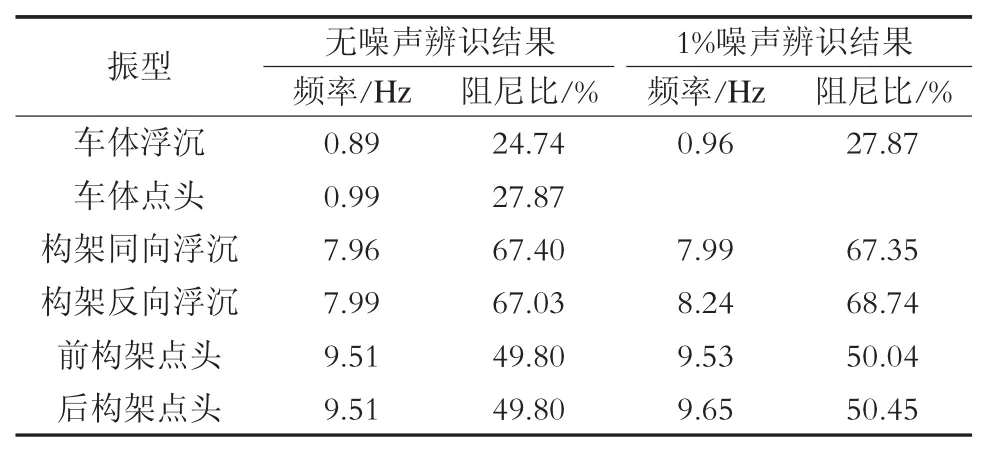
表2 軌道譜反演輸入時運用車輛加速度響應的構架及車體辨識結果
在線路運行條件下,軌道不平順測量比較困難。分析車輛的動力學方程可以看到,車體振動完全由構架輸入所產生,故可將構架作為輸入來辨識車體的模態參數。由于構架位移至車體位移響應與構架加速度至車體加速度響應具有相同的傳遞函數,因此本文也研究了運用構架加速度輸入和車體加速度輸出辨識車體模態參數的效果,辨識結果如表3所示。
從表3可以看到:當噪聲信號很低時,以構架加速度為輸入可完整地辨識出車體的振型,并且辨識精度很高;當噪聲信號增強時,辨識精度隨之變差,但比表2分析結果稍好。此次分析辨識出了點頭振型,而且辨識精度稍高。
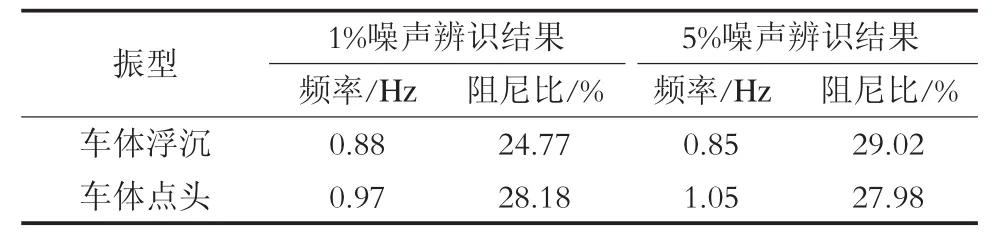
表3 軌道譜反演輸入時以構架加速度響應為輸入的車體辨識結果
3 結語
本文運用N4SID算法對軌道車輛垂向仿真模型進行了模態參數辨識研究。如以車體和構架的位移響應作為系統輸出,并以軌道不平順為隨機輸入、軌道譜反演時域不平順輸入及確定性信號輸入,則即使噪聲信號較大,仍均能獲得良好的識別效果。當以仿真模型的加速度輸出進行辨識時,若輸出信號沒有受到噪聲污染,則能獲得精確的辨識結果;若輸出信號加入了模擬的噪聲信號,則只能識別出較高頻率的模態參數,識別精度也相應受到噪聲信號的影響。如以構架加速度作為輸入,以車體振動響應作為輸出,則在噪聲信號低于5%時,仍能有效識別出車體的振動模態參數。
[1] 周勁松,張洪,任利惠.模態參數在鐵道車輛運行平穩性研究中的運用[J].同濟大學學報(自然科學版),2008,36(3):383.
[2] Bart P,Buido D R.Stochastic System Identification for Operational Modal Analysis:A Review,Journal of Dynamic Systems[J].Measurement,and Control,2001,12(123):659.
[3] 黃金峰,張合新,胡友濤,等.基于有限記憶變遺忘因子的子空間辨識算法[J].控制理論與應用,2012,29(7):893.
[4] 李冬冬.基于子空間辨識算法的壓電懸臂梁振動主動控制研究[D].蘭州:蘭州理工大學,2014.
[5] 沃德·海倫,斯蒂夫·拉門茲,波爾·薩斯.模態分析理論與試驗[M].白化同,郭繼忠,譯.北京∶北京理工大學出版社,2001.