盾構測量若干難題解決措施
商科軍 (中鐵上海工程局集團有限公司技術中心,上海 200436)
在盾構測量工作中,為保證掘進精度,需人工測量盾構機姿態及管片姿態,并對鋼環定位進行人工復核,確保盾構機順利出洞。
1 盾構機姿態人工測量計算
盾構機在掘進過程中應進行人工復核,與盾構機導向系統顯示的偏差進行對比,防止因導向系統參數輸入錯誤、吊籃點誤差或儀器整平誤差引起的盾構姿態偏差超限。
在盾構機掘進過程中,因受場地限制,人工無法測量出盾首及中盾位置的盾構機姿態,只能通過在盾尾設置特征點,以特征點坐標反推出盾首及中盾位置的盾構機姿態。根據實測的特征點坐標,人工計算推算出盾構機姿態的計算復雜且容易出錯。本案例提供一種根據布爾莎七參數模型線性化公式,計算出盾構機姿態,編制計算程序,快速解算出盾構機姿態。
在盾構機始發前,測量出盾首中心點坐標、中盾中心點坐標(掛鋼絲測量)、盾尾中心點坐標(掛鋼絲測量)及盾尾特征點坐標,獲取特征點與盾首、中盾、盾尾的幾何位置關系。在掘進過程中,測量特征點的坐標,利用坐標系轉換,換算出盾首、中盾及盾尾的盾構機姿態。
某工程盾構施工中,定義的TBM坐標系圖1(盾首中心為坐標原點):
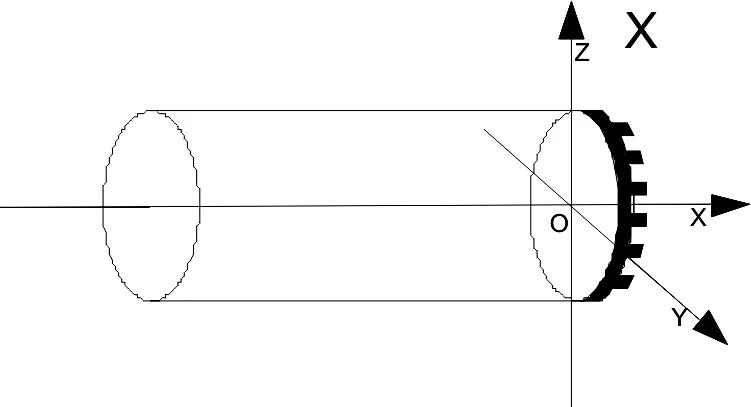
圖1 盾構機TBM坐標系
坐標系轉換采用布爾莎七參數模型,但由于布爾莎七參數是基于微量轉角的轉換模型,故首先需要對此模型公式進行泰勒級數線性化,然后進行迭代計算,以求取坐標系轉換參數。
設轉換前坐標系一點坐標為(x',y',z'),在轉換后坐標系中的坐標為(x,y,z),則根據布爾莎七參數模型可得:
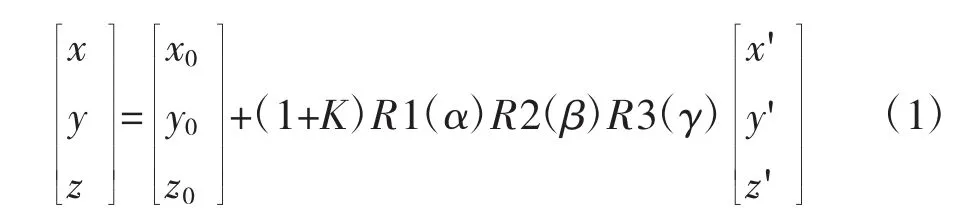
式(1)中(x0,y0,z0)為平移量,K 為縮放比例系數,R1(α),R2(β),R3(γ)為旋轉矩陣,其中:
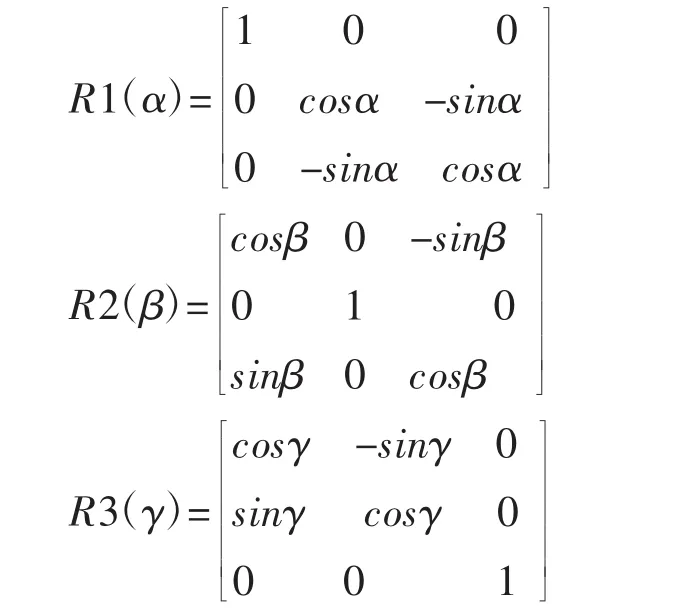
當兩坐標系公共點數大于3個時,可以根據間接平差模型求定以上7個參數。對每個公共點列出誤差方程為:
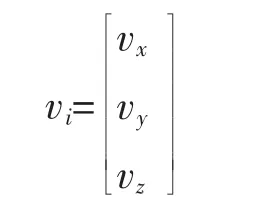
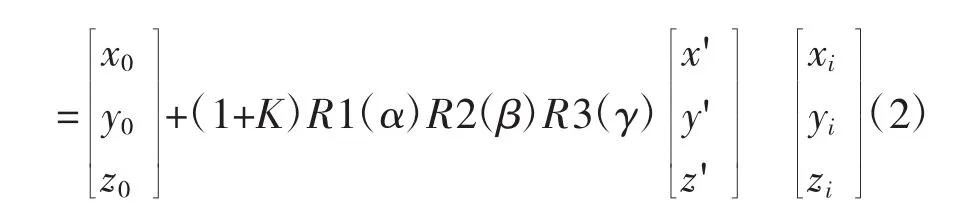
式中 v=(vx,vy,vz)T 為轉換殘差。
將上式寫成間接平差誤差方程的形式為:
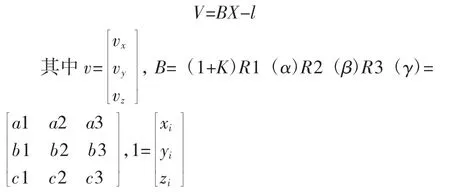
可根據改正數,按間接平差法X=(BTPB)-1BTPL求解7個未知參數,但由于此方法只適用于旋轉角較小的情況,故不能直接進行求解計算,需用泰勒級數對公式進行線性化,得:
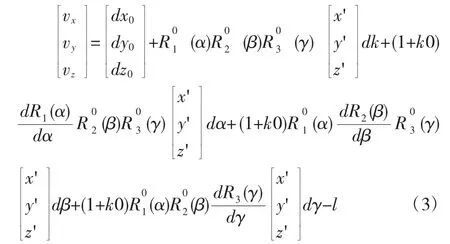
式中V=(Vx,Vy,Vz)T為轉換殘差。將上式寫成間接平差誤差方程的形式為:V=BX-l
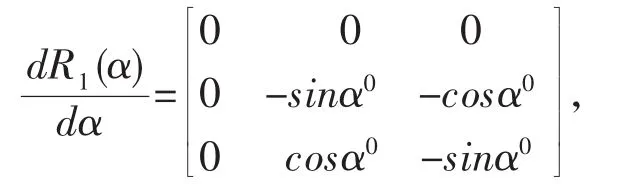
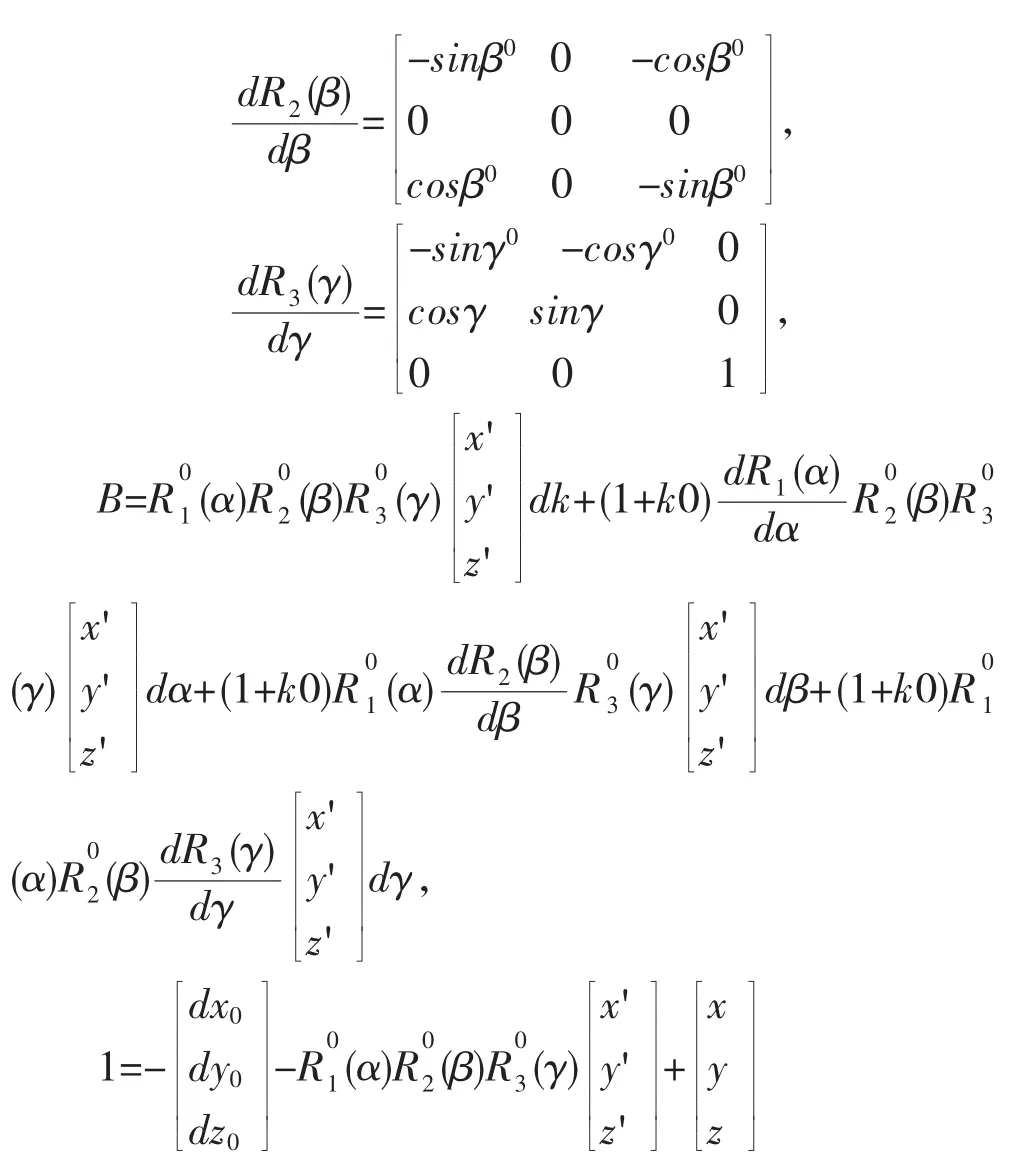
賦予7個參數初始值,按間接平差法X=(BTPB)-1BTPl求解7個未知參數,進行迭代計算,直至x0+y0+z0誤差小于規定的限差,結束迭代計算,結束迭代計算時的7個參數值即為求取的轉換參數,根據轉換參數,求取盾構機盾首、中盾及盾尾的掘進姿態。
案例計算:已知合肥地鐵2號線9標玉蘭大道至天柱路站左線盾構機TBM坐標系特征點坐標及盾構機推進至169環實測特征點坐標如表1所示。
根據(3)式,編制程序,可迅速解算出7個轉換參數,經過8次迭代計算,求解7參數結果如表2所示。
根據求出的7參數,反算出特征點的坐標,并和實測坐標對比,確認轉換無誤。

特征點TBM坐標系坐標與實測施工坐標系坐標 表1

七參數求解值 表2
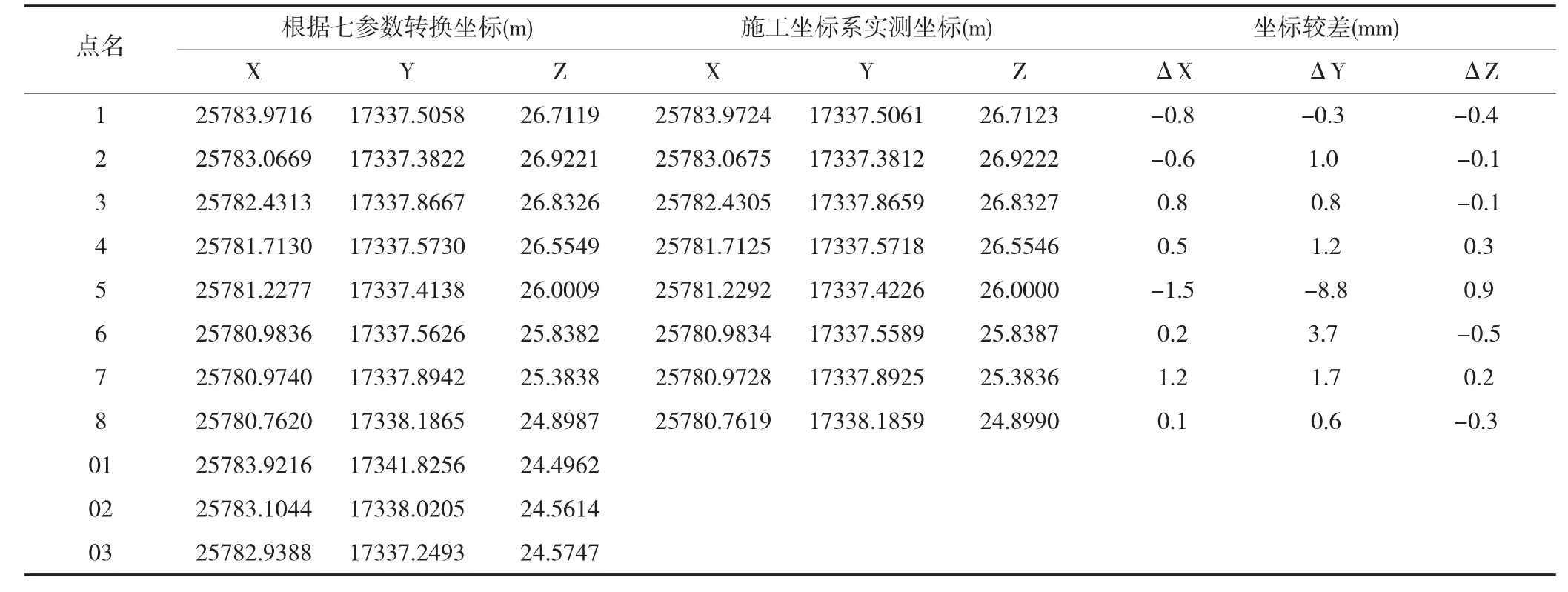
反算坐標值較差及盾首、中盾中心反算坐標 表3
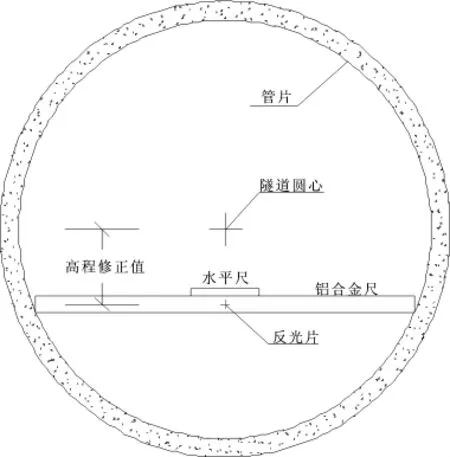
圖2 管片姿態測量
根據反算出的盾首及中盾中心的三維坐標,可計算出目前盾構機姿態偏差,并與盾構導向系統顯示偏差作比較,防止掘進出現偏差。
2 管片姿態人工復核測量計算
為保證管片拼裝姿態,應對拼裝后的管片姿態進行測量,以復核管片姿態誤差。外業測量結束后,進行內業計算,人工內業計算勞動強度大且容易出錯,本案例提供一種根據隧道中心三維軸線和實測管片檢測尺中心坐標推算管片姿態的方法,并用編程實現。管片姿態外業測量如圖2所示,在操作時,實測出反光片中心坐標。
根據實測反光片中心坐標和隧道圓心至反光片的垂直距離,推算出實際的隧道中心三維坐標,利用推算出的隧道中心三維坐標,進行管片姿態內業計算。計算理論如下。
2.1 實測隧道中心點距設計隧道三維軸線坐標點最短距離分析
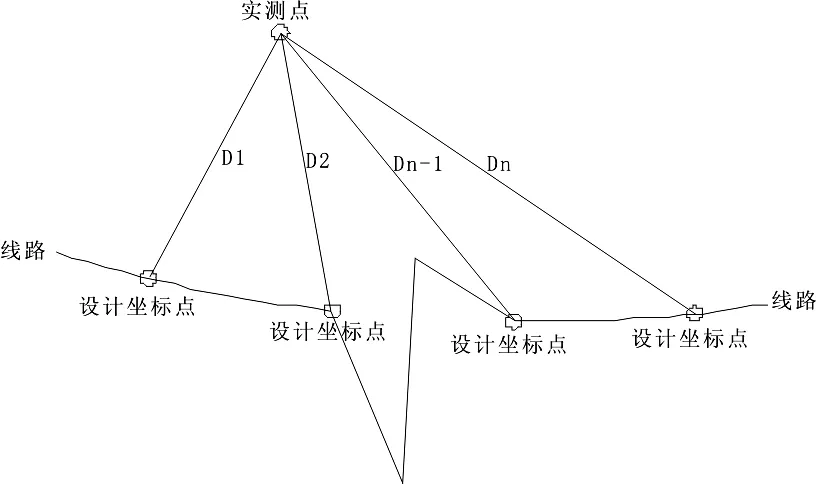
圖3 實測點與線路距離關系
一般按1m間距計算設計隧道三維軸線。計算實測隧道中心點距設計隧道三維軸線上所有實測點的距離(如圖 3 所示),分別為 D1、D2…Dn-1、Dn,分析出最短的距離。假設最短距離為設計隧道三維軸線上第P個點與實測隧道中心點的連線,則存在下列3種情形:
①當D(p-1)=D(p+1)時,說明實測隧道中心點對應的里程與Dp里程相同;
②當D(p-1)>D(p+1),說明實測隧道中心點對應的里程在P點里程與P+1點里程之間;
③當D(p-1)<D(p+1),說明實測隧道中心點對應的里程在P-1點里程與P點里程之間。
2.2 實測隧道中心點偏距計算及位于設計隧道三維軸線右側或左側判斷
實測隧道中心點偏距計算:假設根據求出的實測隧道中心點距設計隧道三維軸線坐標點最短距離,如圖4所示,判斷出實測隧道中心點對應的設計隧道三維軸線里程在R點里程與P點里程之間(R點里程<P點里程),根據余弦定理求出夾角α,實測隧道中心點相對于設計隧道三維軸線的偏距=D|R點→采集點 |×SIN(α)。
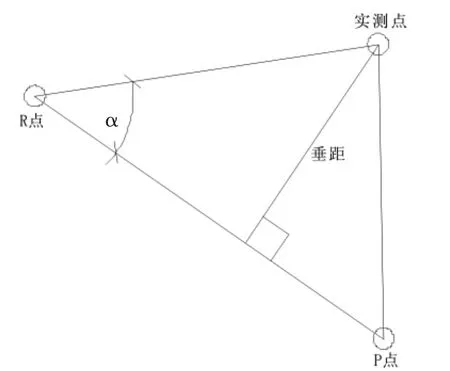
圖4 實測點與線路上R點與P點關系
實測隧道中心點位于設計隧道三維軸線右側或左側的判斷:設R點至P點方位角為F1,R點至采集點方位角為F2,則:
①當 F1≥270。且 <360。時
情形一:當F2>F1且<360時,實測隧道中心點位于設計隧道三維軸線右側;
情形二:當F2≥0且F2≤90。時,實測隧道中心點點位于設計隧道三維軸線右側;
情形三:當F2≥180。且F2<F1時,實測隧道中心點位于設計隧道三維軸線左側。
②當 F1=0。時
情形一:當F2≤90。時,實測隧道中心點位于設計隧道三維軸線右側;
情形二:當F2>270。時,實測隧道中心點位于設計隧道三維軸線左側。
③當 F1>0。且 <90。時
情形一:當 F2>F1 且 F2<180。時,實測隧道中心點位于設計隧道三維軸線右側;
情形二:當 F2>0,且 F2<F1時,實測隧道中心點位于設計隧道三維軸線左側;
情形三:當 F2>270。且 F2>F1 時,實測隧道中心點位于設計隧道三維軸線左側。
④當 F1=90。時
情形一:當F2>F1時,實測隧道中心點位于設計隧道三維軸線右側;
情形二:當F2<F1時,實測隧道中心點位于設計隧道三維軸線左側。
⑤當 F1>90。且 <270。時
情形一:當F2>F1時,實測隧道中心點位于設計隧道三維軸線右側;
情形二:當F2<F1時,實測隧道中心點位于設計隧道三維軸線左側。
2.3 高程偏差計算
設R點高程為HR,P點高程HP,則實測隧道中心點對應設計隧道三維軸線里程的設計高程H采集點設計=HR+[(HP-HR)÷D|RP|]×[D|R點→采集點|×COS(α)],若:
①H采集點實測-H采集點設計>0,則實測隧道中心點高程高于對應設計隧道三維軸線里程的高程;
②H采集點實測-H采集點設計<0,則實測隧道中心點高程低于對應設計隧道三維軸線里程的高程;
③H采集點實測-H采集點設計=0,則實測隧道中心點高程等于對應設計隧道三維軸線里程的高程。
根據計算理論編制計算程序,可迅速計算出管片姿態偏差。
3 洞門鋼環位置復測計算
為保證盾構機順利出洞,需復核接收井鋼環位置,復測鋼環位置時,利用全站儀測量鋼環內徑點。根據實測內徑點坐標,一般利用CAD畫圖進行三點圓心的擬合,工作量較大。本案例提出一種利用空間解析幾何知識,根據實測內徑點坐標擬合出圓心坐標和內徑,編制計算程序,可快速確定鋼環位置是否超限。內業擬合鋼環圓心坐標和內徑理論如下:
已知空間三點的坐標為 A(x1,y1,z1),B(x2,y2,z2),C(x2,y2,z2),求這3個點所確定的空間圓的圓心坐標和半徑。解算過程如下:令圓心坐標為(x,y,z),半徑為R,空間三點確定的平面方程為:
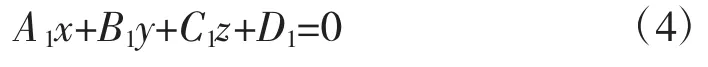
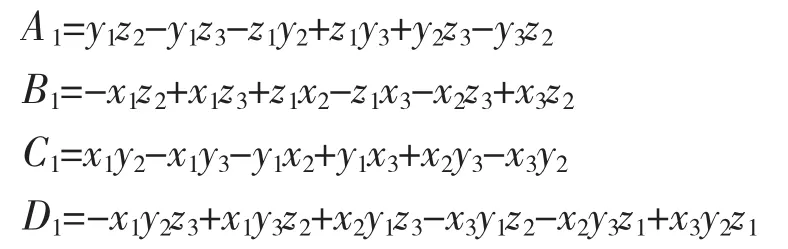
根據圓心到三點的距離均等于半徑長度,可列出下列3式
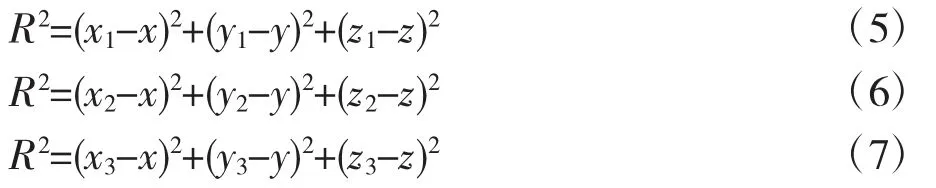
由(5)=(6)得:2(x2-x1)x+2(y2-y1)y+2(z2-z1)z+x+y+z-x-y-z=0,記為:

由(5)=(7)得:2(x3-x1)x+2(y3-y1)y+2(z3-z1)z+x+y+z-x-y-z=0,記為:

聯立(4)、(8)、(9)式,可得:

案例計算:已知武漢地鐵27號線1標新大區間右線始發洞門鋼環內徑點三維坐標如下(表4)。
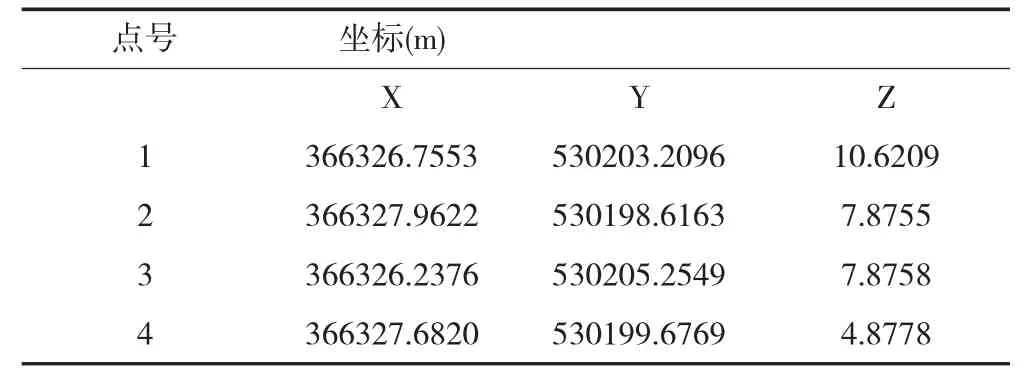
鋼環內徑測量坐標點 表4
根據(10)和(11)式,編制程序,可迅速解出所有點組合的圓心坐標及圓心半徑。求解結果如下(表5)。
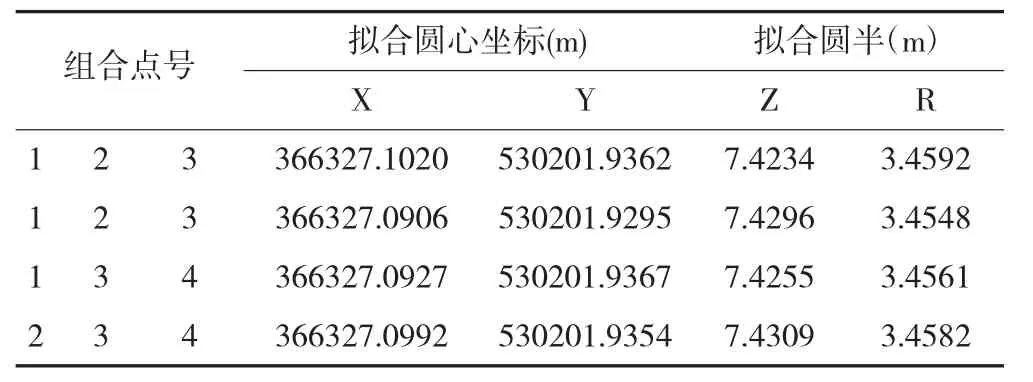
圓心坐標及半徑擬合結果 表5
根據計算結果,剔除粗差較大的數據,取其余點平均值作為圓心坐標及半徑,分析洞門鋼環的偏差。
4 結論
在盾構機姿態人工測量計算中,本文給出了一種適用于大旋轉角的空間三維直角坐標基準的轉換方法。該方法解決了針對大角度的空間三維直角坐標轉換的問題,適用于任意角度的旋轉,計算收斂速度快、易于編制程序實現。在管片姿態人工復核測量計算中,本文給出了坐標反算的各種情形,利用推出的公式,編制程序,可迅速計算管片姿態。在洞門鋼環位置復測計算中,本文推出了根據鋼環內徑點坐標計算鋼環中心坐標公式,根據公式,編制計算程序,可迅速計算出所有內徑點組合反推出的鋼環中心三維坐標,進而分析鋼環中心位置是否超限。
根據本文推導出的計算公式,編制計算程序,可解決盾構測量中的難題,減輕測量人員計算強度,提高盾構測量管理水平。
[1]同濟大學數學系.高等數學下冊[M].北京:高等教育出版社,2007.
[2]同濟大學數學系.線性代數[M].北京:高等教育出版社,2014.
[3]孔祥元,梅是義.控制測量學[M].武漢:武漢大學出版社,2006.
[4]武漢大學測繪學院測量平差學科組.誤差理論與測量平差基礎[M].武漢:武漢大學出版社,2006.
[5]潘國榮等.兩種坐標系轉換計算方法的比較[J].大地測量與地球動力學,2011.
[6]劉東明等.大角度三維基準轉換及公共點的確定[J].測繪通報,2010.
[7]張厚美等.盾構機姿態參數的測量及計算方法[J].現代隧道技術,2004.
[8]潘明華等.盾構機自動導向系統的測量方法研究[J].施工技術,2005.

