基于多層混合濾噪的軸承早期弱故障特征提取方法

呂靖香， 余建波

(同濟(jì)大學(xué) 機(jī)械與能源工程學(xué)院，上海 201804)

滾動(dòng)軸承是各種旋轉(zhuǎn)機(jī)械中使用最廣泛的部件，它的運(yùn)行狀態(tài)往往直接影響整個(gè)機(jī)器的性能[1]。早期軸承故障信號(hào)一般都很微弱，通常被淹沒(méi)在很強(qiáng)的背景噪聲和其他部件的干擾信息中，成分比較復(fù)雜，頻譜范圍大，所以如何抑制噪聲提取出故障特征，成為故障檢測(cè)的關(guān)鍵。

機(jī)械振動(dòng)信號(hào)常用的處理方法包括時(shí)域分析法、頻域分析法和時(shí)頻域分析法，其中時(shí)頻分析法由于能同時(shí)從時(shí)域和頻域揭示信號(hào)成分而得到廣泛應(yīng)用，如小波變換(Wavelet Transform, WT)、經(jīng)驗(yàn)?zāi)B(tài)分解(Empirical Mode Decomposition, EMD)等[2]。相對(duì)于一般時(shí)頻分析方法，局部均值分解(Local Mean Decomposition，LMD)算法不用考慮信號(hào)的平穩(wěn)性，可實(shí)現(xiàn)多分辨率分析，有效改善了EMD算法的端點(diǎn)效應(yīng)，過(guò)包絡(luò)、欠包絡(luò)等問(wèn)題，因此在故障診斷領(lǐng)域取得了應(yīng)用(詳細(xì)的LMD算法過(guò)程本文不再贅述，可參考文獻(xiàn)[3])。但目前LMD在早期故障分析的成果較少，而在降噪方面：一方面主要是將LMD與傳統(tǒng)小波變換[4]、小波包[5]、二代小波[6]相結(jié)合，對(duì)振動(dòng)信號(hào)實(shí)施小波降噪后再進(jìn)行LMD分解，小波分解雖然對(duì)原始信號(hào)實(shí)現(xiàn)了進(jìn)一步細(xì)分，但在抑制噪聲的同時(shí)，有用信號(hào)往往也不可避免地受到損害，這對(duì)后續(xù)LMD分解結(jié)果會(huì)產(chǎn)生嚴(yán)重影響；另一方面與奇異值分解(Singular Value Decomposition, SVD)相結(jié)合，對(duì)振動(dòng)信號(hào)奇異值分解降噪，再對(duì)降噪信號(hào)進(jìn)行LMD分解，最后對(duì)PF分量進(jìn)行包絡(luò)譜分析提取故障特征頻率[7]或者利用LMD分解所得的某一個(gè)PF分量構(gòu)造Hankel矩陣經(jīng)SVD降噪后提取特征頻率[8]。SVD主要應(yīng)用于信號(hào)降噪處理及周期成分的提取，利用信號(hào)與噪聲的能量可分性，對(duì)含噪信號(hào)構(gòu)成矩陣進(jìn)行分解，僅保留信號(hào)特征奇異值達(dá)到去噪目的，具有零相位偏移性[9]，但直接對(duì)原始信號(hào)利用SVD消噪很可能會(huì)損失這些弱故障特征信息，只針對(duì)某一PF分量進(jìn)行SVD分解后提取故障頻率，則會(huì)人為的忽略掉其他故障相關(guān)頻率，造成診斷的片面性。

針對(duì)早期振動(dòng)信號(hào)受噪聲干擾嚴(yán)重的問(wèn)題，本文提出一種基于LMD的多層混合濾噪方法(Local Mean Decomposition-Multilayer Hybrid De-noising, LMD-MHD)。首先基于LMD分解原理，將原始振動(dòng)信號(hào)分解成若干PF分量，第一層利用多指標(biāo)綜合決策PF選擇方法篩選出含故障信息豐富的有效分量，其次在第二層對(duì)每個(gè)有效分量分別進(jìn)行小波閾值消噪(Wavelet Threshold De-noising, WTD)排除脈沖干擾對(duì)奇異值的影響，然后合并，最后基于SVD在降噪方面的優(yōu)良特性，利用合并信號(hào)構(gòu)造Hankel矩陣進(jìn)行第三層濾噪。

1 基于LMD的多層混合濾噪算法

針對(duì)軸承故障早期振動(dòng)信號(hào)中的特征成分極易被噪聲信號(hào)淹沒(méi)而不能及時(shí)檢測(cè)的問(wèn)題，結(jié)合LMD的自適應(yīng)性，保留信息完整性和突出信號(hào)局部故障特征等方面的優(yōu)勢(shì)，以及SVD在消除隨機(jī)噪聲成分和提取信號(hào)周期成分上的優(yōu)良特性，同時(shí)考慮其局限性，提出基于LMD-MHD的故障診斷方案。方案流程圖如圖1所示，方案具體步驟如下：

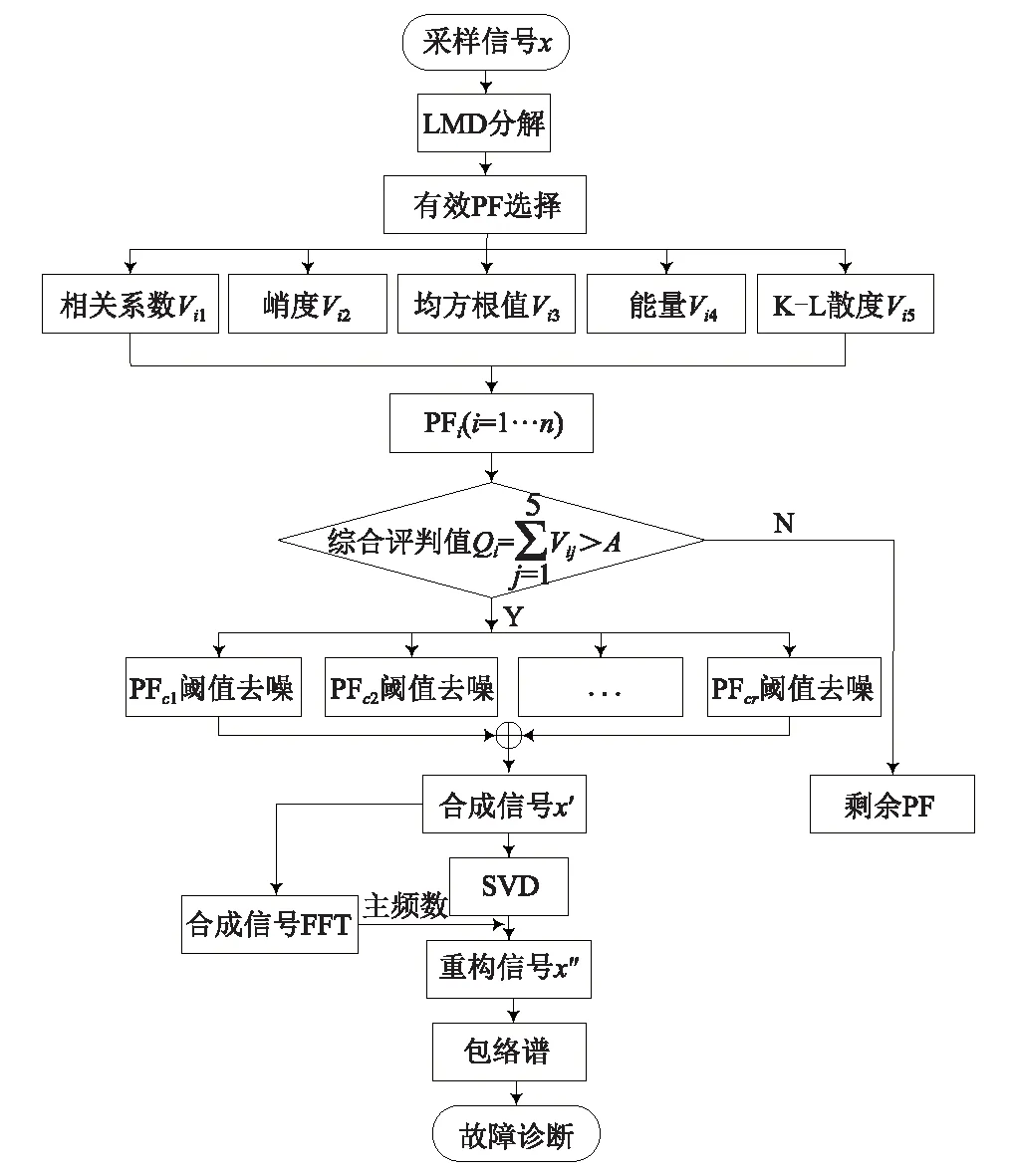
圖1 基于LMD-MHD的故障診斷流程圖 Fig.1 The flowchart of LMD-MHD method

(1)對(duì)采樣信號(hào)x進(jìn)行LMD分解，得到多個(gè)PF分量；

(2)計(jì)算出每個(gè)PF分量的峭度、均方根值，以及相對(duì)于原始振動(dòng)信號(hào)的相關(guān)系數(shù)、能量占比和K-L散度等指標(biāo)值；

(3)使用多指標(biāo)綜合決策方法得到各分量的綜合評(píng)判值Qi，篩選出綜合評(píng)判值較大的PFcr分量；

(4)對(duì)PFcr分量分別進(jìn)行小波閾值降噪作為奇異值分解的前置濾波處理，抑制脈沖干擾，將閾值處理后的PFcr分量構(gòu)成一維合成信號(hào)x′；

(5)對(duì)合成信號(hào)x′進(jìn)行快速傅里葉變換，得到合成信號(hào)的主頻個(gè)數(shù)；

(6)以信號(hào)x′數(shù)據(jù)長(zhǎng)度的一半作為矩陣列數(shù)，構(gòu)造Hankel矩陣并進(jìn)行奇異值分解；

(7)根據(jù)合成信號(hào)主頻個(gè)數(shù)確定降噪階次，SVD逆過(guò)程重構(gòu)得到重構(gòu)信號(hào)x″；

(8)包絡(luò)解調(diào)重構(gòu)信號(hào)x″，提取故障特征頻率，實(shí)現(xiàn)故障診斷。

1.1 第一層濾噪——多指標(biāo)綜合決策PF選擇方法

一般PF分量的選擇方法僅僅依靠單一指標(biāo)如K-L散度[10]、相關(guān)系數(shù)[11]等來(lái)衡量PF與原始信號(hào)的相似程度，或者利用峭度[12]、均方根值[13]等某一時(shí)域特征參數(shù)來(lái)區(qū)別PF。相關(guān)系數(shù)和K-L散度的計(jì)算都是以原始信號(hào)為基準(zhǔn)，僅僅量化了PF分量和原始信號(hào)的相似程度，在早期振動(dòng)信號(hào)較為復(fù)雜的情況下，難以準(zhǔn)確反映PF分量與信號(hào)中其他重要成分的相似程度。峭度對(duì)沖擊信號(hào)十分敏感，尤其適合早期故障診斷，但當(dāng)故障進(jìn)一步加深時(shí)，峭度指標(biāo)有回落跡象,穩(wěn)定性不好。均方根值的穩(wěn)定性很好，但對(duì)早期故障敏感度一般。結(jié)合峭度和均方根值便可以兼顧敏感性和穩(wěn)定性。所以僅通過(guò)一種指標(biāo)來(lái)選擇PF忽略了參數(shù)本身隨故障加深的變化以及噪聲的影響。本文基于噪聲對(duì)時(shí)域特征參數(shù)的影響及其參數(shù)形式簡(jiǎn)單等問(wèn)題，同時(shí)考慮到振動(dòng)信號(hào)的沖擊性，各指標(biāo)對(duì)于不同階段故障的適應(yīng)性和量化能力[14]，結(jié)合相關(guān)系數(shù)、峭度、均方根值、能量占比(各PF分量與原始信號(hào)的能量比)、K-L散度五項(xiàng)指標(biāo)，提出多指標(biāo)綜合決策PF選擇方法，避免了單一指標(biāo)對(duì)某些信號(hào)的誤判性，實(shí)現(xiàn)對(duì)PF分量的準(zhǔn)確選取。

在多指標(biāo)綜合決策PF選擇方法中，設(shè)PF1,PF2, …,PFn是對(duì)故障信號(hào)局部均值分解產(chǎn)生的n個(gè)分量；相關(guān)系數(shù)H1，峭度H2，均方根值H3，能量占比H4，K-L散度H5是評(píng)價(jià)PF分量的5個(gè)評(píng)價(jià)指標(biāo)；Vi1,Vi2, …,Vi5是第i個(gè)分量PFi關(guān)于指標(biāo)Hj(j=1～5)的價(jià)值評(píng)定量。價(jià)值評(píng)定量為對(duì)應(yīng)指標(biāo)值的歸一化結(jié)果：

(1)

式中：Hij是PFi的第j個(gè)指標(biāo)值(K-L散度取倒數(shù)后歸一化)。PFi的綜合評(píng)判值為：

(2)

取綜合評(píng)判值較大的幾個(gè)PF為有效分量進(jìn)行后續(xù)處理。

1.2 第二層濾噪——基于小波閾值的PF信號(hào)降噪

原始信號(hào)經(jīng)LMD分解之后，進(jìn)一步突顯了故障信號(hào)的局部特征信息，但噪聲抑制作用不明顯，經(jīng)篩選之后的PF分量仍含有大量噪聲。考慮到奇異值分解的局限性，需進(jìn)行第二層濾噪處理，利用小波閾值降噪方法去除PF分量中的脈沖干擾，初步提高其信噪比。

PF分量按分解出來(lái)的順序，其包含的頻率成分呈現(xiàn)明顯的下降趨勢(shì)，而不同的小波基具有不同的特性，可以根據(jù)PF的頻率分布特性來(lái)選擇小波基和分解層數(shù)，采用啟發(fā)式閾值選取規(guī)則。對(duì)有效PF分量作離散小波變換，小于某一臨界閾值的小波系數(shù)主要是由噪聲引起的，予以舍去；大于臨界閾值的小波系數(shù)主要由信號(hào)引起的，直接保留(硬閾值方法)或者按照某一固定量向零收縮(軟閾值方法)。得到估計(jì)小波系數(shù)之后進(jìn)行小波重構(gòu)便得到去噪后的信號(hào)。

硬閾值函數(shù)為：

(3)

軟閾值函數(shù)為：

(4)

式中：wj, k表示第j層小波分解的第k個(gè)系數(shù)；λ為閾值估計(jì)值。

1.3 第三層濾噪——信號(hào)奇異值分解

對(duì)于一個(gè)實(shí)矩陣A∈Rm×n，無(wú)論其行列是否相關(guān)，必定存在正交矩陣U∈Rm×n和正交矩陣V∈Rm×n，使得下式成立

A=UDVT

(5)

式中：D是對(duì)角陣，D∈Rm×n，表示為D=(diag(σ1,σ2, …，σq),0)(m≤n)或其轉(zhuǎn)置(m>n)，0表示零矩陣，q=min(m,n)，且有σ1≥σ2≥…σq≥0即矩陣A的奇異值。

SVD將振動(dòng)信號(hào)空間分解為加噪信號(hào)子空間和噪聲信號(hào)子空間，降噪過(guò)程中僅保留了前面若干個(gè)對(duì)應(yīng)加噪信號(hào)子空間的較大奇異值，而其余奇異值全部置零。然而當(dāng)背景噪聲較強(qiáng)尤其存在脈沖干擾時(shí)，SVD降噪算法中所保留的某些奇異值以噪聲貢獻(xiàn)為主，由此得到的重構(gòu)信號(hào)含有的噪聲信息較多[15]，降噪效果不佳。此外，SVD對(duì)隨機(jī)噪聲濾波效果明顯，對(duì)脈沖噪聲的抑制作用并不理想[16]。所以先對(duì)信號(hào)進(jìn)行小波閾值降噪去除幅值較大的異常值，再進(jìn)行SVD可以更有效地消除信號(hào)中的隨機(jī)噪聲成分，提高周期成分的提取能力。

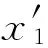
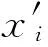
(6)

式中：si表示真實(shí)信號(hào)；wi表示噪聲信號(hào)；構(gòu)造Hankel矩陣如下

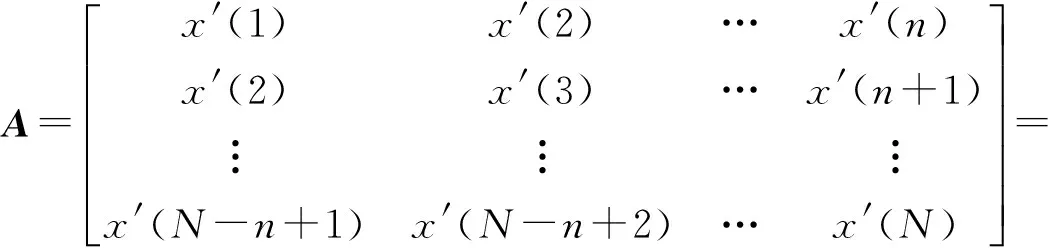
(7)

式中：1

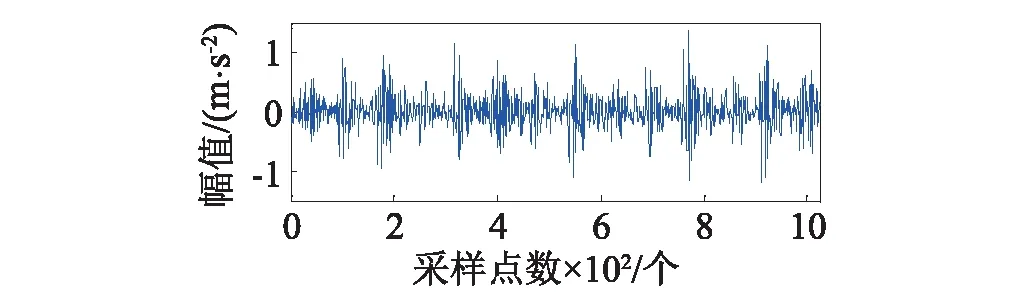
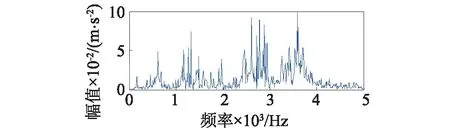
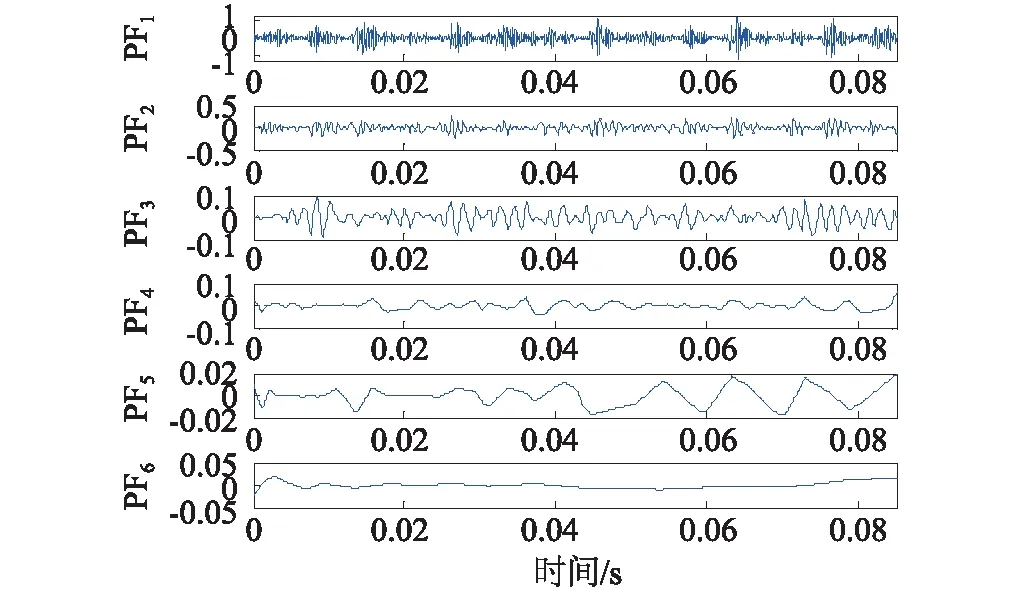
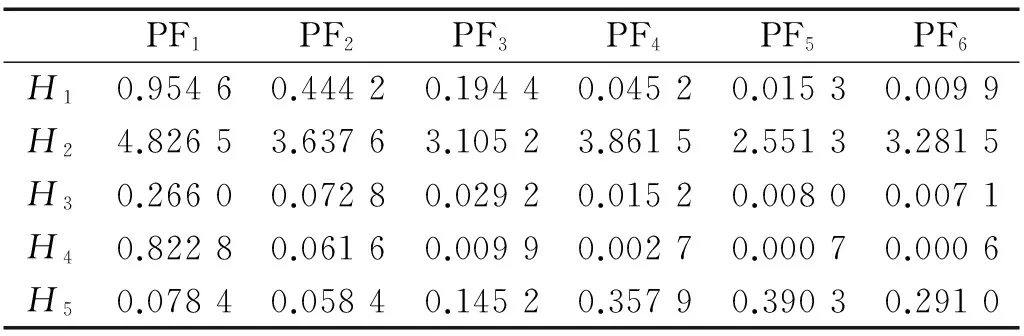
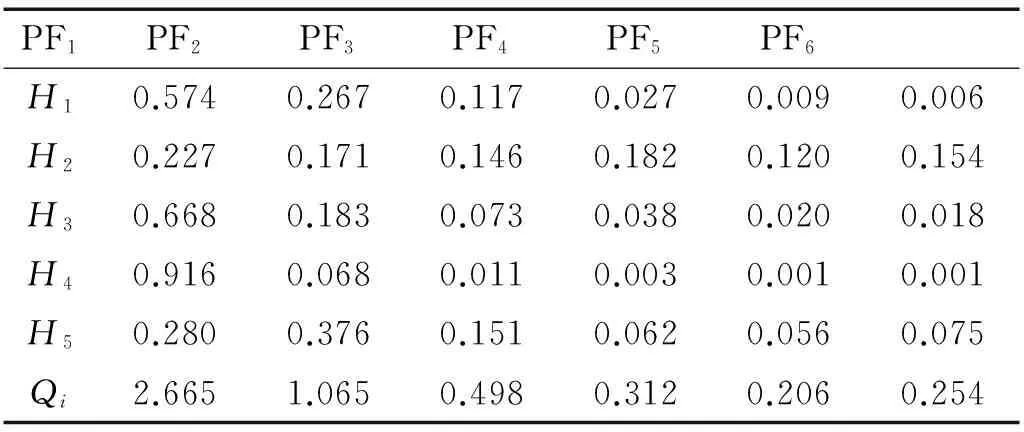
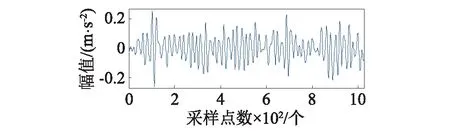
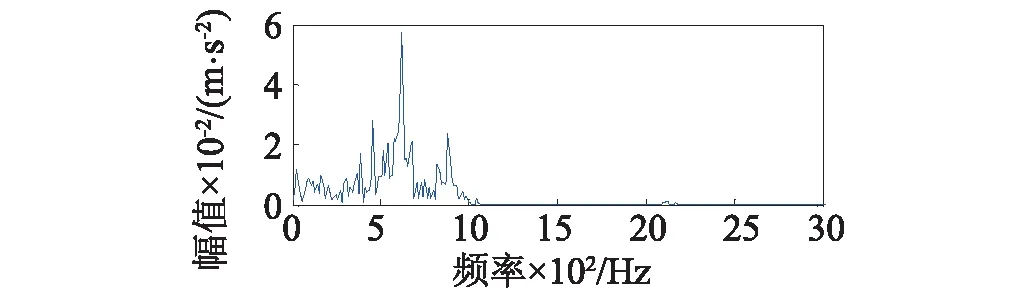
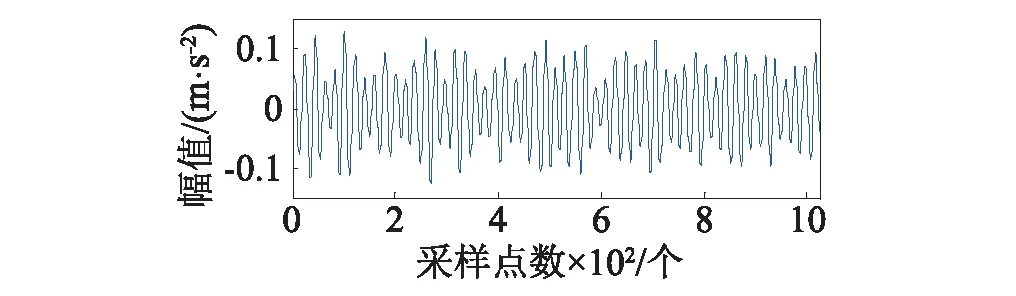
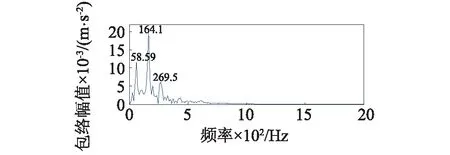
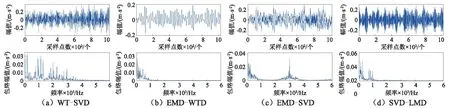
對(duì)含噪信號(hào)進(jìn)行SVD降噪的關(guān)鍵在于降噪階次的選擇，當(dāng)所選階次過(guò)低時(shí)，易造成信息缺失，階次過(guò)高則帶入更多噪聲。考慮本文在對(duì)軸承信號(hào)進(jìn)行SVD之前經(jīng)過(guò)了閾值濾波降噪，所以可根據(jù)合成信號(hào)快速傅里葉變換后主頻個(gè)數(shù)的2倍來(lái)確定有效秩階次，其原理在于由第個(gè)非零奇異值重構(gòu)得到重構(gòu)信號(hào)分量的頻率成分均為源信號(hào)的頻率成分組成,而由較大的奇異值重構(gòu)得到的分量信號(hào)其頻率成分與源信號(hào)中主頻率相對(duì)應(yīng)[17]。但它的缺陷在于當(dāng)原始信噪比特別低時(shí)，有用信號(hào)會(huì)被噪聲完全淹沒(méi),傅里葉變換結(jié)果中有用信號(hào)頻率與噪聲頻率難以區(qū)分，采取此方法的前提是在奇異值分解之前有小波閾值消噪來(lái)預(yù)先提高PF分量的信噪比。

2 早期故障診斷實(shí)例

本文選用美國(guó)凱斯西儲(chǔ)大學(xué)電氣工程實(shí)驗(yàn)室的軸承實(shí)驗(yàn)數(shù)據(jù)[18]進(jìn)行分析，試驗(yàn)臺(tái)由功率為1.5 kW的電動(dòng)機(jī)、扭矩傳感器/譯碼器、測(cè)力計(jì)和電器控制裝置等組成。測(cè)試軸承6205-2RS SKF深溝球軸承。其參數(shù)如表1～2。

表1 軸承結(jié)構(gòu)參數(shù)Tab.1 Structure parameters of bearing

表2 軸承內(nèi)圈故障數(shù)據(jù)Tab.2 Fault data of inner race

軸承的損傷是用電火花加工的單點(diǎn)損傷，內(nèi)圈損傷直徑為0.018 cm，損傷直徑較小可視為早期故障信號(hào)。由圖2的軸承內(nèi)圈故障數(shù)據(jù)的時(shí)域波形和幅值譜可以看出，信號(hào)包含大量的脈沖和隨機(jī)噪聲，頻譜成分復(fù)雜，難以觀察到周期性的調(diào)制特征。對(duì)故障信號(hào)進(jìn)行LMD分解得到6個(gè)PF分量如圖3所示，每個(gè)分量對(duì)應(yīng)的相關(guān)系數(shù)和峭度等指標(biāo)計(jì)算結(jié)果如表3所示，采用多指標(biāo)綜合決策PF選擇方法算出綜合評(píng)判值Qi。如表4所示，PF1的綜合評(píng)判值遠(yuǎn)大于其他PF的值，說(shuō)明PF1所包含的故障沖擊成分最多，PF5和PF6的綜合評(píng)判值較小，予以舍去，從而保留前四個(gè)PF分量。

(a)時(shí)域波形

(b)幅值譜圖2 軸承內(nèi)圈故障數(shù)據(jù)的時(shí)域波形及幅值譜 Fig.2 Time-domain waveform and amplitude spectrum of bearing signal

圖3 內(nèi)圈信號(hào)LMD分解結(jié)果 Fig.3 LMD results of b signal

PF1PF2PF3PF4PF5PF6H10.95460.44420.19440.04520.01530.0099H24.82653.63763.10523.86152.55133.2815H30.26600.07280.02920.01520.00800.0071H40.82280.06160.00990.00270.00070.0006H50.07840.05840.14520.35790.39030.2910

表4 PF分量的綜合評(píng)判值計(jì)算Tab.4 Comprehensive evaluation values of PFs

分別對(duì)前四個(gè)PF進(jìn)行小波閾值降噪并重組，得到合成信號(hào)如圖4(a)所示，時(shí)域波形里的噪聲得到了大幅削減，但周期性成分和調(diào)制現(xiàn)象尚未體現(xiàn)。從圖4(b)的快速傅里葉變換的結(jié)果中可以看出大量干擾頻率已被去除，頻率成分位于中高頻段，主要頻率個(gè)數(shù)有3個(gè)。

(a)時(shí)域波形

(b) 幅值譜圖4 第二層濾噪處理結(jié)果 Fig.4 Results of second layer de-noising

進(jìn)而對(duì)合成信號(hào)進(jìn)行奇異值分解，有效秩階次為主頻個(gè)數(shù)的兩倍即取6，從而得到重構(gòu)信號(hào)如圖5(a)所示，重構(gòu)信號(hào)呈現(xiàn)出非常清晰的周期性沖擊特征，噪聲基本濾除。對(duì)重構(gòu)信號(hào)進(jìn)行包絡(luò)譜分析，從圖5(b)中可以明顯看到164.1 Hz的峰值頻率，和軸承內(nèi)圈故

(a)時(shí)域波形

(b)包絡(luò)譜圖5 LMD-MHD濾噪處理結(jié)果 Fig.5 Results of LMD-MHD filtering

障理論頻率162 Hz非常接近，同時(shí)存在58.59 Hz的頻率與轉(zhuǎn)軸基頻2倍頻59.90相對(duì)應(yīng)，269.5 Hz的頻率與轉(zhuǎn)軸基頻9倍頻269.55基本一致，這些都跟軸承內(nèi)圈故障特征相吻合，由此可以判定軸承內(nèi)圈出現(xiàn)了故障。

采用其他四種典型方法(WT-SVD[19], EMD-WTD[20], EMD-SVD[21], SVD-LMD)對(duì)故障信號(hào)進(jìn)行分析，結(jié)果如圖6所示，圖6(a)為對(duì)振動(dòng)信號(hào)進(jìn)行小波分解，利用每個(gè)細(xì)節(jié)信號(hào)構(gòu)造Hankel矩陣進(jìn)行SVD，選擇最佳降噪階次進(jìn)行對(duì)應(yīng)細(xì)節(jié)信號(hào)的重構(gòu)，最后小波重構(gòu)還原的信號(hào)，可以看出最終還原的信號(hào)中仍然含有大量噪聲，故障特征難以辨識(shí)。圖6(b)為對(duì)故障信號(hào)進(jìn)行EMD分解，并對(duì)前幾個(gè)高頻本征模態(tài)分量(Intrinsic Mode Function, IMF)進(jìn)行小波閾值降噪后與低頻分量重構(gòu)的結(jié)果，包絡(luò)譜中含有近似的故障頻率，但缺乏周期性，調(diào)制現(xiàn)象不明顯。圖6(c)是在EMD分解之后對(duì)幾個(gè)高頻IMF分量進(jìn)行SVD降噪再與低頻分量重構(gòu)所得結(jié)果，存在一定的調(diào)制波形，但是噪聲干擾較嚴(yán)重。SVD-LMD方法則是先對(duì)原始信號(hào)進(jìn)行SVD分解再對(duì)降噪后的信號(hào)進(jìn)行LMD分解，最后對(duì)相關(guān)系數(shù)最大的PF分量進(jìn)行包絡(luò)譜分析，結(jié)果如圖6(d)所示，相關(guān)系數(shù)最大的PF1分量中仍然含有較多噪聲，其包絡(luò)譜也未見內(nèi)圈故障頻率。而圖5中本文所提方法的結(jié)果明顯優(yōu)于其他幾種方法。綜上，LMD-MHD算法能夠有效濾除隨機(jī)噪聲和脈沖干擾，提取出淹沒(méi)在強(qiáng)背景噪聲中的弱故障特征。

圖6 其他典型方法處理結(jié)果比較 Fig.6 Results of Other typical methods

3 結(jié) 論

針對(duì)軸承早期故障信號(hào)受噪聲干擾嚴(yán)重，故障特征不易提取的問(wèn)題，本文提出了基于LMD的多層混合濾噪處理的解決方法。考慮LMD和SVD的優(yōu)缺點(diǎn)，采用更加全面合理的多指標(biāo)綜合決策PF分量選擇辦法，保證有用信息不丟失，提高特征提取的精度；利用有效秩的階次與信號(hào)主頻個(gè)數(shù)存在2倍的關(guān)系確定重構(gòu)奇異值個(gè)數(shù)的方法簡(jiǎn)單高效；以小波閾值濾噪作為SVD的前置濾波器，減少脈沖干擾，確保需要保留的較大奇異值中所含噪聲成分很少；小波閾值濾噪和奇異值分解兩者相輔相成，有效地去除了大量隨機(jī)噪聲和脈沖干擾，使得軸承故障信號(hào)的調(diào)制特性得以呈現(xiàn)。軸承故障診斷實(shí)例的結(jié)果表明了該方法的有效性和適用性。

[ 1 ] YU J. Local and nonlocal preserving projection for bearing defect classification and performance assessment [J]. IEEE Transactions on Industrial Electronics, 2012, 59(5): 2363-2376.

[ 2 ] 王衍學(xué), 何正嘉, 訾艷陽(yáng), 等. 基于LMD的時(shí)頻分析方法及其機(jī)械故障診斷應(yīng)用研究[J].振動(dòng)與沖擊, 2012, 31(9): 9-12.

WANG Yanxue, HE Zhengjia, ZI Yanyang, et al. Several key issues of local mean decomposition method used in mechanical fault diagnosis [J]. Journal of Vibration and Shock, 2012, 31(9): 9-12.

[ 3 ] SMITH J S. The local mean decomposition and its application to EEG perception data [J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.

[ 4 ] SONG R, MA M, XIE C. Application of vibration signal analysis method based on wavelet and LMD [J].Journal of Information & Computational Science, 2015, 12(4): 1503-1510.

[ 5 ] 孫偉, 熊邦書, 黃建萍, 等. 小波包降噪與LMD相結(jié)合的滾動(dòng)軸承故障診斷方法[J].振動(dòng)與沖擊, 2012, 31(18): 153-156.

SUN Wei, XIONG Bangshu, HUANG Jianping, et al. Fault diagnosis of a rolling bearing using wavelet packet de-noising and LMD [J]. Journal of Vibration and Shock, 2012, 31(18): 153-156.

[ 6 ] LIU Z, HE Z, GUO W, et al. A hybrid fault diagnosis method based on second generation wavelet de-noising and local mean decomposition for rotating machinery [J]. Isa Transactions, 2016, 61: 211-220.

[ 7 ] 王建國(guó)，李建, 萬(wàn)旭東. 基于奇異值分解和局域均值分解的滾動(dòng)軸承特征提取方法[J].機(jī)械工程學(xué)報(bào)，2015, 51(3): 104-110.

WANG Jianguo, LI Jian, WAN Xudong. Fault feature extraction method of rolling bearings based on singular value decomposition and local mean decomposition [J]. Journal of Mechanical Engineering, 2015, 51 (3): 104-110.

[ 8 ] 馬朝永, 劉茜, 段建民. 基于LMD與奇異值差分譜的滾動(dòng)軸承故障診斷方法[J]. 北京工業(yè)大學(xué)學(xué)報(bào), 2014, 40(2): 182-188.

MA Chaoyong, LIU Qian, DUAN Jianmin. Fault diagnosis method of rolling bearings based on LMD and singular value difference spectrum [J].Journal of Beijing University of Technology, 2014, 40(2): 182-188.

[ 9 ] 聶振國(guó), 趙學(xué)智. PCA與SVD信號(hào)處理效果相似性與機(jī)理分析[J]. 振動(dòng)與沖擊, 2016, 35(2): 12-17.

NIE Zhenguo, ZHAO Xuezhi. Similarity of signal processing effect between PCA and SVD and its mechanism analysis [J]. Journal of Vibration and Shock, 2016, 35(2): 12-

17.

[10] SUN J, XIAO Q, WEN J, et al. Natural gas leak location with K-L divergence-based adaptive selection of Ensemble Local Mean Decomposition components and high-order ambiguity function [J]. Journal of Sound and Vibration, 2015, 347: 232-245.

[11] 楊梅, 陳思漢, 吳昊, 等. LMD濾噪算法及在旋轉(zhuǎn)機(jī)械轉(zhuǎn)子故障診斷中的應(yīng)用[J].噪聲與振動(dòng)控制, 2015, 35(2): 160-164.

YANG Mei, CHEN Sihan, WU Hao, et al. An improved LMD-based de-noising algorithm for fault diagnosis of rotating machinery [J]. Noise and Vibration Control, 2015, 35(2): 160-164.

[12] 唐貴基, 王曉龍. 基于局部均值分解和切片雙譜的滾動(dòng)軸承故障診斷研究[J]. 振動(dòng)與沖擊, 2013, 32(24): 83-

88.

TANG Guiji, WANG Xiaolong. Fault diagnosis of roller bearings based on local mean decomposition and slice bispectrum [J]. Journal of Vibration and Shock, 2013, 32(24): 83-88.

[13] 鞠萍華, 秦樹人, 趙玲. 基于LMD的能量算子解調(diào)方法及其在故障特征信號(hào)提取中的應(yīng)用[J].振動(dòng)與沖擊, 2011, 30(2): 1-4.

JU Pinghua, QIN Shuren, ZHAO Ling. Energy operator demodulating approach based on LMD and its application in extracting characteristics of a fault signal [J]. Journal of Vibration and Shock, 2011, 30(2): 1-4.

[14] YU J. Bearing performance degradation assessment using locality preserving projections [J]. Expert Systems with Applications, 2011, 38(6): 7440-7450.

[15] 曾鳴，楊宇，鄭近德,等. μ-SVD降噪算法及其在齒輪故障診斷中的應(yīng)用[J]. 機(jī)械工程學(xué)報(bào)， 2015， 51(3)： 95-103.

ZENG Ming, YANG Yu, ZHENG Jinde, et al. μ-SVD based de-noising method and its application to gear fault diagnosis [J]. Journal of Mechanical Engineering, 2015, 51 (3): 95-103.

[16] 徐峰，劉云飛，宋軍. 基于中值濾波-SVD和EMD的聲發(fā)射信號(hào)特征提取[J].儀器儀表學(xué)報(bào)，2011，32(12)： 2712-2719.

XU Feng, LIU Yunfei, SONG Jun. Feature extraction of acoustic emission signals based on median filter-singular value decomposition and empirical mode decomposition [J]. Chinese Journal of Scientific Instrument, 2011, 32(12): 2712-2719.

[17] 錢征文，程禮，李應(yīng)紅. 利用奇異值分解的信號(hào)降噪方法[J]. 振動(dòng)、測(cè)試與診斷, 2011， 31(4)： 459-463.

QIAN Zhengwen, CHENG Li, LI Yinghong. Noise reduction method based on singular value decomposition [J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31 (4): 459-463.

[18] Case western reserve university bearing data center website [EB/OL].http∥csegroups.case.edu/bearingdatacenter/pages/download-data-file, 2011-05-11.

[19] 趙學(xué)智, 葉邦彥, 陳統(tǒng)堅(jiān). 基于小波—奇異值分解差分譜的弱故障特征提取方法[J]. 機(jī)械工程學(xué)報(bào), 2012, 48(7): 37-48.

ZHAO Xuezhi, YE Bangyan, CHEN Tongjian. Extraction method of faint fault feature based on wavelet-SVD difference spectrum [J]. Journal of Mechanical Engineering, 2012, 48(7): 37-48.

[20] 邵忍平, 曹精明, 李永龍. 基于EMD小波閾值去噪和時(shí)頻分析的齒輪故障模式識(shí)別與診斷[J].振動(dòng)與沖擊，2012, 31(8): 96-101.

SHAO Renping, CAO Jingming, LI Yonglong. Gear fault pattern identification and diagnosis using time-frequency analysis and wavelet threshold de-noising based on EMD [J]. Journal of Vibration and Shock, 2012, 31(8): 96-

101.

[21] HAN T, JIANG D, WANG N. The fault feature extraction of rolling bearing based on emd and difference spectrum of singular value [J]. Shock and Vibration, 2016: 1-14.