高速鐵路救援起重機多支撐機構力學解算研究*

劉 永，李 揚，張雷雷*，趙延治，劉康榮，王淵明，于躍斌

(1.中車齊齊哈爾車輛有限公司 大連研發中心 ,遼寧 大連 116052；2.燕山大學 機械工程學院，河北 秦皇島 066004；3.武漢鐵路局 機務處，湖北 武漢 430071；4.秦皇島煙草機械有限公司，河北 秦皇島 066004；5.中車齊齊哈爾車輛有限公司，黑龍江 齊齊哈爾 161002)

0 引 言

高速鐵路為人們提供方便快捷的同時，也為鐵路救援提出了新的課題。高鐵線路橋線比大[1]，救援的關鍵問題是解決橋梁、線路承載能力的限制。現有國內外鐵路起重機下車結構主要采用4支腿的結構形式，由于高鐵橋梁承載能力的限制，不僅單個支腿所能夠承受的最大載荷較地面作業大為降低，此外也對作業起重機多個支腿間載荷均布的程度提出了較高的要求。倘若依然沿用原有結構形式的普通鐵路救援起重機，會帶來巨大的安全隱患。德國的GOTTWALD公司發明的旋轉式伸縮平衡重技術是鐵路救援起重機的一重大進步，該公司的產品在瑞士、日本、韓國等市場上占有率高[2]。

為此，一種多支撐系統被提了出來。該系統在原有起重機4支腿支撐的基礎上引入4條輔助支腿，并且使輪軌同時承擔載荷，達到降低單個支腿工作載荷目的，滿足高鐵救援起重工作的嚴苛條件。

關于4支腿支撐結構形式的支腿反力計算已有大量研究人員對此做出研究。李以申[3]分析了傳統4支腿模型支腿反力兩種不同計算方法的謬誤。榮國瑞[4]應用力學方法在考慮支腿剛度的條件下求解得到了支腿反力，并以反向補償的方式解決了支腿起翹后的反力計算問題。房曉文[5]在同時考慮車架大梁扭轉及支腿彎曲變形的基礎上，推導出了起重機支腿反力的計算公式。但是隨著起重機工作環境的變化，例如高架橋、凍原等特殊的作業環境下，使用4支腿起重機可能會引起支腿載荷超限、載荷分布不均等問題的出現，這時候就需要增加支撐的數量。王健[6]提出了一種五支腿起重機支腿反力計算方法。劉振國[7]使用力學中的相關計算方法得到了一種八支腿起重機支腿反力的計算方法。

針對一種高速鐵路救援起重機多支撐機構，本文使用結構力學中的超靜定結構力法原理[8]來進行解析計算，并對實際算例進行剛柔耦合仿真加以驗證。

1 高鐵救援起重機多支撐結構及其力學模型

整個起重機承載結構由車架大梁、4個內側伸縮支腿，4個外側擺動支腿以及輪軌支撐組成，整個下車結構為對稱布置如圖1所示。

圖1 高鐵救援起重機下車結構模型

由于輪軌和車體是通過轉向架連接，本研究在把車體簡化成受力模型時將輪軌受力集中到前后兩個轉向架上，即在原8支腿支撐結構中增加兩個支點，支點位置在中央主支撐梁上，類似于其他承載支腿，兩個支點對負載和力矩進行承載。

受力分別為F9、F10如圖2所示。

圖2 高鐵起重機力學模型

該結構為空間七次超靜定結構。

2 高次超靜定結構的力法計算方法

力法是最為基本的求解超靜定問題的方法，力法的基本思想是將超靜定結構通過去除多余約束來拆解成靜定結構。

一次超靜定結構如圖3所示。

圖3 一次超靜定結構

靜定結構如圖4所示。

圖4 靜定結構

本研究通過在靜定結構條件下建立的變形協調方程來過渡到超靜定結構。

由受力圖可知：靜定結構中簡支梁受3個未知力(或力矩)Fx、Fy、M，可用平面任意力系的3個平衡方程全部求出；一次超靜定結構中簡支梁在B點受到額外的一個支座反力X1，此時梁總共受到4個約束力無法由3個平衡方程求出全部未知力(或力矩)。

在超靜定結構中遇到的新問題就是求解超出平衡方程個數的未知力(或力矩)。一般可以通過構造變形協調方程來增補方程個數，從而使方程個數與未知力(或力矩)個數相同。

下面討論n次超靜定結構的基本方程建立方法。當結構為n次超靜定結構時(n>2)，結構中的基本未知量為n個多余未知力X1、X2、…、Xn。力法的基本體系是從原結構中去掉n個多余約束，而代之以相應的n個多余未知力后所得到的靜定結構，力法的基本方程是在n個多余約束處的n個變形條件，即基本體系中沿多余未知力方向的位移應與原結構中相應的位移相等。

在線性變形體系中，根據疊加原理，n個變形條件通常可寫為：

(1)

式中：ΔiP—由載荷產生的沿Xi方向的位移；δij—由單位力Xj=1產生的沿Xi方向的位移，常稱為柔度系數。

其中，當位移方向與相應的力的正方向相同時，位移符號規定為正。根據位移互等定理，系數δij和δji是相等的。

關于載荷作用下的位移ΔiP，結構力學中提供了相關的計算公式：

(2)

式中：MP，FP，TP—代表由實際加載載荷P引起的結構的彎矩、軸向力和扭矩；Mi，Fi，Ti—代表由虛設單位載荷Xi引起的結構的彎矩、軸向力和扭矩。

柔度系數δij即由單位力Xj=1產生的沿Xi方向的位移，可以由以下公式計算：

(3)

式中：Mj，Fj，Tj—代表由虛設單位載荷Xj引起的結構的彎矩、軸向力和扭矩；Mi，Fi，Ti—代表由虛設單位載荷Xi引起的結構的彎矩、軸向力和扭矩；

由此，將計算所得各項柔度系數和載荷作用下沿各分支方向產生的位移代回式(1)中，加上垂直方向力平衡方程和X軸、Y軸方向轉矩平衡方程，即可求解得到各分支方向承受反力數值。

3 高鐵救援起重機多支撐結構力學解算

該多支撐結構為7次超靜定結構，取6、7、8支腿為基本支腿，列出相關的7次超靜定力法方程：

(4)

至此，該多支撐結構力法方程系數已完全建立。本研究假設從圖2建立的坐標系原點到轉向架連接點處的距離為相關支點的計算用支腿長度，利用鐵木辛柯梁理論計算出相關的截面等效剛度。

將7次超靜定結構的力及力矩平衡方程加入到力法方程中，得到包含10個未知數和10個方程的線性方程組：

(5)

式中：ai—代表第i條支腿在坐標系中X軸方向坐標值；bi—代表第i條支腿在坐標系中Y軸方向坐標值；

取兩種不同的工況，編寫Matlab程序計算結果如下。

(1)起重載荷為160 t，車體質量為110 t，起重力矩為5×108N·m，使起重臂回轉一周，所得曲線如圖5所示。

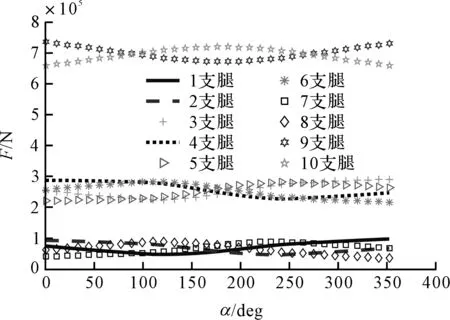
圖5 計算所得160 t負載下各支點負載情況

從分析結果可以看到，在給定工況下，受力最大的支腿為前后兩個轉向架，承載了大部分載荷，負載最大時為7.5×105N；隨著起重機上車起重臂的轉動，各支腿受力情況發生變化，與轉動方向同一Y軸半區的4條支腿受力增加，而另4條支腿受力減少，反之亦然。在工作過程中，內側伸縮支腿受力最大值約為3×105N，外側伸縮支腿受力最大值約為105N。

(2)起重載荷為200 t，車體質量為110 t，起重力矩為7×108N·m，使起重臂回轉一周，所得曲線如圖6所示。

圖6 計算所得200 t負載下各支點負載情況

從分析結果可以看到，在給定200 t工況下，受力最大支腿依然為前后兩個轉向架，承載了絕大多數的負載，負載最大時為9×105N；隨著起重機上車起重臂的轉動，各支腿受力情況發生變化，與轉動方向同一Y軸半區的4條支腿受力增加，而另4條支腿受力減少，反之亦然。在工作過程中，內側伸縮支腿受力最大值約為3.5×105N，外側展開支腿受力最大值約為1.2×105N。

4 剛柔耦合仿真結果對比

由于引入了轉向架作為支撐點，建立了新的三維模型，并對模型重新劃分網格[9]如圖7所示。

圖7 動力學仿真軟件中的柔性體模型

(1)在仿真軟件中設定工作條件為：

起重量160 t，起重力矩5×108N·m。

仿真曲線如圖8所示。

圖8 160 t時起重臂轉動一周支腿受力曲線

從仿真結果看出，受力最大的支腿為前后兩個轉向架，承載了絕大多數的負載，負載最大時為大約8×105N。內側伸縮支腿最大負載為2.7×105N。

(2)在仿真軟件中設定工作條件為：

起重量200 t，起重力矩7×108N·m。

仿真曲線如圖9所示。

圖9 200 t時起重臂轉動一周支腿受力曲線

從仿真結果看出，受力最大支腿依然為前后兩個轉向架，承載了絕大多數的負載，負載最大時為大約9.5×105N。內側伸縮支腿承載支腿最大負載為3×105N。

由于建立的是剛柔耦合仿真模型，仿真過程中設定的負載較大時，多支撐結構會出現一定的振動現象，但對支反力的影響不大。軟件仿真的整個工作過程中，受力最大的支點為前后兩個轉向架，負載最大時為大約7.5×105N。展開支腿的受力的最大值約為3×105N。

與Matlab程序計算的解析解相比，數值和趨勢基本一致，驗證了解析模型的正確性。

5 結束語

本文利用空間高次超靜定原理求解了一種高速鐵路救援起重機多支撐機構支撐反力，并對機構進行了剛柔耦合仿真，仿真結果與解析解結果趨勢基本一致，驗證了解析模型的正確性，該方法可以推廣到類似多支撐機構的支撐反力計算中。

在引入輪軌受力之后，相對于八支腿支撐受力，各支腿的受力大為減小，從而降低了高架橋面受到的破壞風險，提升了安全性；同時從計算結果的對比中可以看出，在較大工作載荷下，支腿的起翹現象得到了改善，進一步提升了起重機工作的穩定性與安全性。

在建立支腿系統剛柔耦合模型時，忽略了一些因素的影響，有必要通過實驗進行數據的采集，進行更精確的建模。

此外，為了精確分析多支撐結構的動態性能，需要對其進行動力學建模，從而為高速鐵路救援起重機下車部分支撐機構的設計提供可靠的依據。

參考文獻(References):

[1] 孟 鋼.滬杭高鐵橫潦涇大橋快速施工管理實踐研究[D].成都：西南交通大學土木工程學院,2015.

[2] EBRAHIMI M, GHAYOUR M, MADANI S M, et al. Swing angle estimation for anti-sway overhead crane control using load cell[J].InternationalJournalofControl,AutomationandSystems.2011,9(2):300-309.

[3] 李以申.試評輪胎式起重機支腿反力的幾種計算方法[J].建筑機械,1989(2):48-52.

[4] 榮國瑞.汽車起重機支腿壓力的新算法[J].重慶建筑大學學報,1997,19(3):49-54.

[5] 房曉文.汽車起重機支腿反力簡化計算方法與實驗驗證[J].起重運輸機械,2012(6):89-92.

[6] 王 健,周 靜,崔曉琳，等.五支腿起重機支腿力計算方法研究[J].農業裝備與車輛工程,2009(11):19-21.

[7] 劉振國,滕儒民,吳海帆,等.一種八支腿起重機支腿反力研究[J].機械設計與制造,2015(5):12-14.

[8] 龍馭球,包世華,匡文起,等.結構力學教程(Ⅰ)[M].北京：高等教育出版社,2000.

[9] 徐國寶，馬金鳳，王延軍，等.基于ADAMS的跌落式裝箱機動力學仿真研究[J].包裝與食品機械，2016(1)：44-47.