電阻應變片敏感柵結構參數對應變傳遞的影響研究*
許藝青,楊曉翔,韋鐵平,姚進輝
(1.福州大學 石油化工學院,福建 福州 350116;2.福州大學 機械工程及自動化學院,福建 福州 350116;3.泉州師范學院,福建 泉州 362000;4.福建工程學院 機械與汽車工程系,福建 福州350118;5.福建省計量科學研究院,福建 福州 350003)
0 引 言
因具有靈敏度高、測量精度高和穩定性強等特點,電阻應變式傳感器被廣泛應用于許多領域。電阻應變片作為敏感元件,是電阻應變式傳感器的重要組成部分,其結構尺寸直接影響傳感器的測量性能。
Fuyu等[1]設計出20 t的柱式傳感器,并推導出了傳感器非線性誤差的計算公式。基于彈性力學理論求解了柱式負荷傳感器長徑比為0.6~1.0彈性體的應變值分布規律,韋鐵平等[2]發現長徑比對端部效應的靈敏度有重大影響。雷一鳴[3]討論了應變片靈敏系數的變化對測量結果的影響,并給出了降低此影響的方法。Weymouth等[4]對各種金屬電阻應變片進行介紹,并對應變片粘貼提出建議。Younis等[5]針對被測試件的高應變區域提出鉆孔法使其應力集中,對該區域應變片選擇提出了建議。Sarangi等[6]針對有邊緣裂紋的試樣,利用DS技術得出應變片的最佳貼片位置。段然等[7]通過拉伸試驗研究影響應變片測試精度的因素,提出了提高應變片測量精度的措施。Tang K等[8]研制了一種PID溫度控制系統的實驗裝置,完成了箔式應變片在77 K~293 K的溫度范圍內的敏感系數修正。張佳明等[9]建立了應變片標定系統,在20 ℃~800 ℃范圍內對應變片的靈敏度、滯后和蠕變進行了標定,證明了高溫應變片在800 ℃時具有良好的性能。Zike等[10]建立了電阻應變式傳感器彈性體和應變片的三維模型,利用有限元法研究發現基底彈性模量對測量結果影響很大,并對其進行了修正。王彪等[11]等通過建立電阻應變計的二維應變傳遞模型,對其應變傳遞機理進行了分析,研究表明膠接層橫向寬度越寬、厚度越薄、彈性模量越大,應變傳遞過渡區越小,平均應變傳遞率越大。王文瑞等[12]和胡玉梅[13]建立了簡支梁、膠層和柵絲的三維模型,研究絲式應變片的應變分布,結果表明敏感柵越細、膠層厚度和彈性模量越小,測量精度越高,柵絲間距和長度具有最優值,并通過實驗進行了驗證。Larry Burrow[14]通過有限元分析了箔式應變片的基底、箔材的厚度和材料及應變片端環尺寸對應變片性能的影響。
綜上所述,目前對于電阻應變式傳感器的研究主要集中在傳感器的靜態特性、端部效應、應變片的粘貼工藝、應變傳遞原理、溫度和結構參數對絲式電阻應變片性能的影響上,對箔式電阻應變片敏感柵幾何參數對應變傳遞的影響研究則較少。
本研究通過建立三維簡化模型,利用ANSYS有限元軟件對不同敏感柵結構進行模擬,揭示其對應變片性能和電阻應變式傳感器的應變傳遞誤差影響。
1 電阻應變片工作原理及結構
電阻應變片是一種用途廣泛的高精度力學傳感元件,主要由敏感柵、基底、覆蓋層及引出線所組成[15]。
敏感柵是應變片最重要的組成部分,常用材料有康銅、鎳鉻合金、鐵鉻鋁合金、鉑合金等。敏感柵結構主要由邊柵、橫柵、測量柵、過渡柵和焊接柵組成,如圖1所示。

圖1 敏感柵的典型結構B—敏感柵全長;L—敏感柵基長;W—柵寬;a—單柵絲寬度;h—柵絲間距
2 有限元模型建立及其驗證
為研究傳感器在測量狀態下的應變分布,本研究建立了“等強度梁—基底—敏感柵—覆蓋層”的有限元結構模型,各部分材料的力學性能[16]和幾何參數如表1所示。
網格劃分時對等強度梁與應變片基底交界處進行網格加密劃分,有限元網格模型如圖2所示。

表1 各部分力學性能和幾何尺寸
各部分均采用八節點六面體實體單元solid185,模擬時將三者設置綁定約束使其粘接起來,等強度梁的左端全約束,在右端施加載荷50 kN的力值。

圖2 有限元網格模型
根據材料力學知識可知,等強度梁貼片位置沿x軸方向的應變εs和自由端的撓度f為:
(1)
(2)
式中:Es—等強度梁彈性模量,MPa;F—等強度梁端部的外荷載,N;x—應變片中點與加載點的距離,mm;bs—等強度梁貼片位置的寬度,mm;ts—等強度梁的厚度,mm;Ls—等強度梁全長,mm。
等強度梁撓度云圖和x方向應變云圖分別如圖3、圖4所示。

圖3 等強度梁撓度云圖

圖4 等強度梁x方向應變云圖
從圖中可以看出,等強度梁自由端的撓度為12.021 1 mm,與理論值偏差為1.39%,貼片位置的應變εs為6.90×10-4,與理論值偏差為2.54%,仿真結果與理論值計算基本一致。
應變片整體x方向應變云圖如圖5所示。

圖5 應變片x方向應變云圖
本研究將所有節點x方向的應變提取出來做平均值,繪制的應變分布圖如圖6所示。

圖6 應變片x方向應變分布
從圖6可知,等強度梁向應變片傳遞應變時,基底與敏感柵之間存在應變過渡區,即圖中a區域,該規律與Zike[10]研究結果一致。從圖5中可以看出,應變片的兩端不受力的作用,傳感器受到外力作用產生的應變,是由各層之間的剪切應變傳遞給應變片敏感柵的,應力突變區域越小,越有利于應變傳遞。
取應變片測量柵中間20個節點x方向應變的平均值,作為應變片的測量值,則從傳感器彈性體到敏感柵的應變傳遞率α為:
(3)
式中:εh—敏感柵x方向的應變。
3 應變片結構參數對應變傳遞的影響
影響傳感器性能的主要因素之一是應變片敏感柵的結構參數,如其敏感柵材料、柵絲橫截面積、柵絲間距、柵絲長度等。因此,本文基于有限單元法,重點分析這幾個參數對應變片應變分布規律和應變傳遞誤差的影響。敏感柵的焊接柵的截面積遠大于柵絲截面積,由上述有限元結果可知焊接柵上的應變很小,故下述分析忽略焊接柵的影響。
3.1 敏感柵材料
應變片和等強度梁幾何參數一定時,模擬康銅、鐵鉻鋁合金、鎳鉻鋁合金、鉑銥合金4種合金下應變片敏感柵和基底的應變分布如圖7、圖8所示。

圖7 不同敏感柵材料敏感柵x方向應變分布
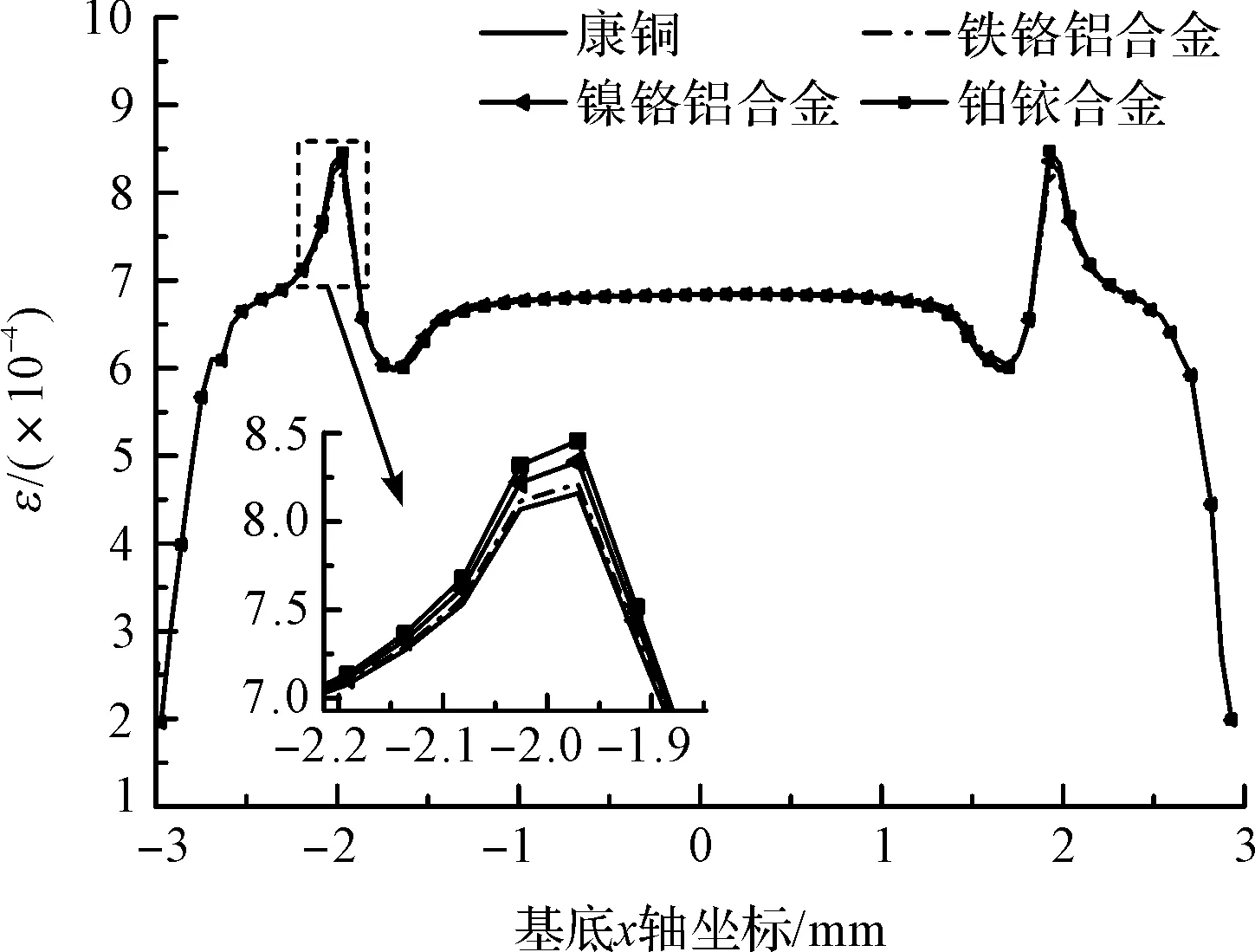
圖8 不同敏感柵材料基底x方向應變分布
從圖上可以看出,敏感柵材料彈性模量越小,敏感柵的應變分布越均勻,基底在應變突變區的x方向應變越小,即應變過渡區越小。
不同敏感柵材料應變傳遞誤差如表2所示。

表2 不同敏感柵材料力學性能和應變傳遞誤差
從表2中可以看出,康銅、鐵鉻鋁合金、鎳鉻鋁合金、鉑銥合金的應變傳遞誤差分別為0.87%、1.01%、1.16%、1.3%,彈性模量從169 GPa增加到232 GPa時,誤差增加了0.43%,即隨著敏感柵材料彈性模量的增大,應變傳遞誤差也隨之增大,但影響幅度不大。
3.2 敏感柵厚度
本研究保持其他參數不變,選取敏感柵厚度t為0.003 mm、0.005 mm、0.01 mm 3種情況進行模擬。不同敏感柵厚度時敏感柵和基底的應變分布如圖9、圖10所示。
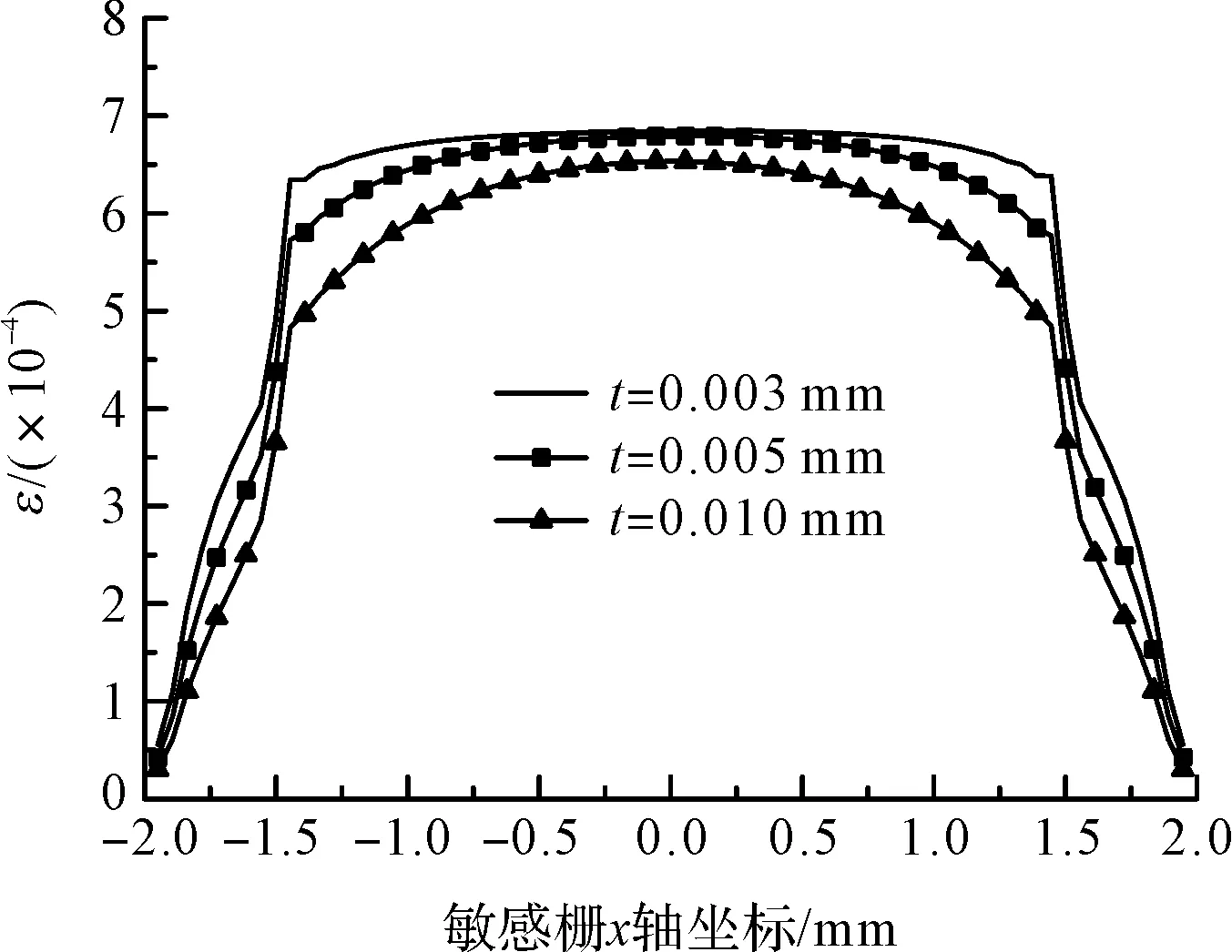
圖9 不同敏感柵厚度敏感柵x方向應變分布

圖10 不同敏感柵厚度基底x方向應變分布
從圖上可以看出,敏感柵厚度對應變片應變分布影響很明顯,敏感柵厚度越薄,柵絲上的應變分布越均勻,基底在應變突變區的x方向應變越小,即應變過渡區越小。
不同敏感柵厚度的應變傳遞誤差如表3所示。

表3 不同敏感柵厚度的應變傳遞及誤差
從表3中可以看出,箔材厚度為0.003 mm、0.005 mm、0.01 mm時應變傳遞誤差分別為0.87%、1.59%、5.51%,厚度從0.003 mm增加到0.01 mm,誤差增大了4.64%,應變傳遞誤差隨箔材厚度增加而增加,即敏感柵越薄越有利于應變傳遞。但是,由實際經驗可知,應變片敏感柵越薄越容易損壞,因此應根據實際情況選擇敏感柵厚度。
3.3 敏感柵柵絲長寬比
敏感柵柵絲長度和寬度決定了柵絲數目和應變片幾何尺寸,為此本研究模擬了柵絲長寬比為:20∶1、50∶1和70∶1三種情況。不同敏感柵柵絲長寬比時敏感柵和基底的應變分布圖如圖11、圖12所示。

圖11 不同柵絲長寬比敏感柵x方向應變分布
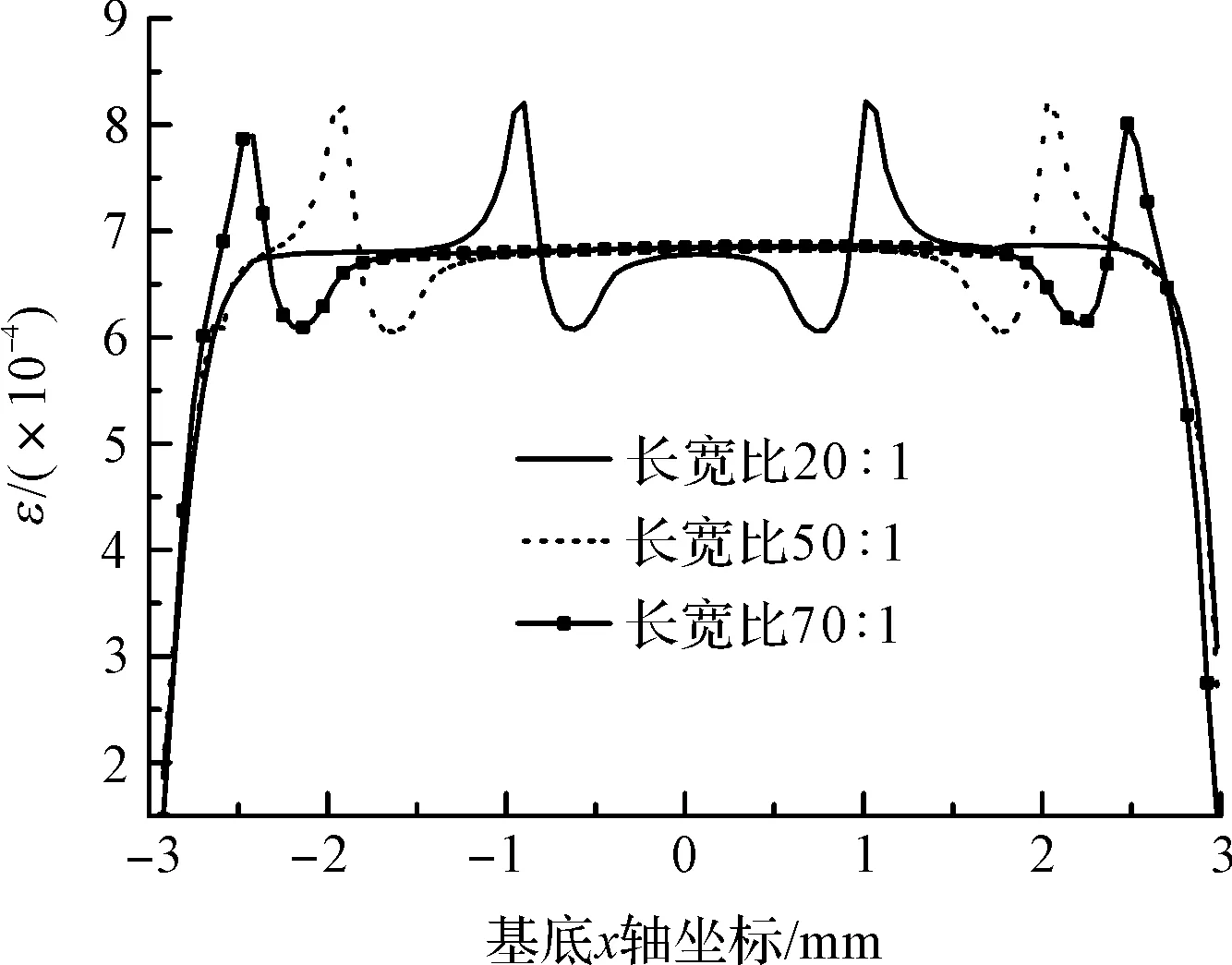
圖12 不同柵絲長寬比基底x方向應變分布
從圖上可以看出,長寬比越大,柵絲的應變分布越均勻,應變傳遞率越大。
不同柵絲長寬比時應變傳遞誤差如表4所示。
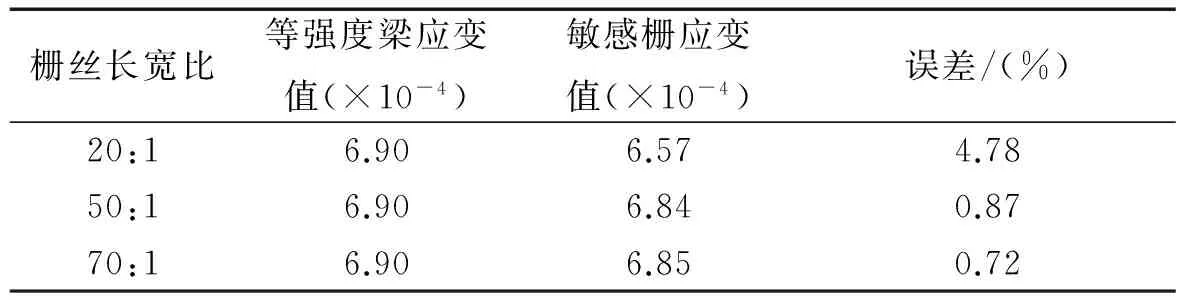
表4 不同柵絲長寬比的應變傳遞及誤差
從表4中可以看出,柵絲長寬比為20:1、50:1和70:1時,應變傳遞誤差分別為4.78%、0.87%、0.72%。長寬比從20:1增加到70:1時,誤差減小了4.02%,在一定范圍內,應變傳遞誤差隨長寬比增加而減少。該分析結果與文獻[12]實驗結果相一致。
3.4 敏感柵柵絲間距
當應變片柵絲長度一定時,柵絲間距越大,則敏感柵柵寬越寬。取柵絲間距h為0.056 mm、0.112 mm和0.28 mm,不同柵絲間距時敏感柵和基底的應變分布如圖13、圖14所示。

圖13 不同柵絲間距敏感柵x方向應變分布

圖14 不同柵絲間距基底x方向應變分布
從圖上可以看出,柵絲間距越大,柵絲上的應變分布越均勻,基底應變突變區的x方向應變越小,即應變過渡區越小。
不同柵絲間距時應變傳遞誤差如表5所示。

表5 不同柵絲間距的應變傳遞及誤差
由表5可見,柵絲間距為0.056 mm、0.112 mm和0.28 mm時,應變傳遞誤差分別為1.16%、0.89%、1.01%,柵絲間距從0.056 mm增大到0.112 mm時,應變傳遞誤差減小了0.27%,而從0.112 mm增大到0.28 mm時,應變傳遞誤差增加了0.12%,這說明柵絲間距存在最優值,該仿真結果與文獻[12]實驗結果相一致。
4 結束語
(1)本研究建立了等強度梁和應變片三維模型,通過有限元法模擬出的應變傳遞率達99.1%,可見該模型能正確地反映傳感器的應變傳遞。從有限元結果可知,敏感柵的主要受力部位在測量柵中間位置,每根柵絲受力較均勻,并向兩端逐漸遞減至零。在應變傳遞過程中,基底與敏感柵之間存在應變過渡區;
(2)本研究分析了敏感柵材料、厚度、柵絲長寬比、柵絲間距變化時應變片應變分布規律及應變傳遞誤差。研究表明:敏感柵材料彈性模量越小、厚度越薄,敏感柵的應變分布越均勻,基底在應變突變區的x向應變和切應變越小,即應變過渡區越小;柵絲長寬比越大,柵絲的應變分布越均勻。箔材彈性模量越小、厚度越薄和柵絲寬比越大,應變傳遞誤差越小,越有利于應變傳遞,越能準確反映彈性體變形;敏感柵柵絲間距存在最優值;
(3)本文計算結果給出了敏感柵各結構參數對應變片應變分布和傳遞誤差的影響,為電阻應變式傳感器應變片的結構設計和應變片的選擇提供了依據。
參考文獻(References):
[1] FUYU W, FANG M. Factors influencing output non-linearity error of a high-precision load sensor and the error calculation[J].FiniteElementsinAnalysis&Design,2001,37(4):341-347.
[2] 韋鐵平,楊曉翔,姚進輝,等.柱式負荷傳感器的長徑比對端部效應的影響[J].應用力學學報,2015,32(6):1038-1043
[3] 雷一鳴.電阻應變計應變傳遞研究及誤差分析[J].科學技術與工程,2011(32):8096-8100.
[4] WEYMOUTH L J, STARR J, DORSEY J. Bonded resistancestraingages[J].ExperimentalMechanics,1979,19(3):112-120.
[5] YOUNIS N T, KANG B. Averaging effects of a strain gage[J].JournalofMechanicalScience&Technology,2011,25(1):163-169.
[6] SARANGI H, MURTHY K S R K, CHAKRABORTY D. Experimental verification of optimal strain gage locations for theaccurate determination of mode I stress intensity factors[J].EngineeringFractureMechanics,2013,110(1):189-200.
[7] 段 然,肖立峰.材料拉伸試驗中影響應變片測量精度的因素分析[J].機械設計,2013,30(12):76-80.
[8] TANG K, SHA L, LI Y J, et al. Measurement of thermal expansion at low temperatures using the strain gage method[J].JournalofZhejiangUniversityenceA,2014,15(5):323-330.
[9] 張佳明,王文瑞,聶 帥.高溫電阻應變片特性參數標定實驗研究[J].中國測試,2014,40(5):25-28.
[10] ZIKE S, MIKKELSEN L P. Correction of gauge factor for strain gauges used in polymer composite testing[J].ExperimentalMechanics,2014,54(3):393-403.
[11] 王 彪,劉 騰,徐敬龍,等.金屬粘貼式電阻應變計應變傳遞分析[J].中國測試,2016,42(8):1-6.
[12] 王文瑞,張佳明,聶 帥.高溫應變接觸式測量精度影響因素研究[J].固體火箭技術,2015(3):439-444.
[13] 胡玉梅,張方建,邵毅敏,等.應變片敏感柵結構參數對測量精度的影響[J].重慶大學學報:自然科學版,2013,36(12):21-27.
[14] 尹福炎.箔式應變片結構模型與有限元分析[J].衡器,2009,38(5):47-50.
[15] STEIN P. Strain gage history and the end of the twentieth century[J].ExperimentalTechniques,2010,25(2):15-16.
[16] 耿漢生.應變膠性能與應變計的工作特性[J].傳感器用技術,1990(4):43-46.

