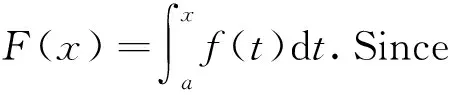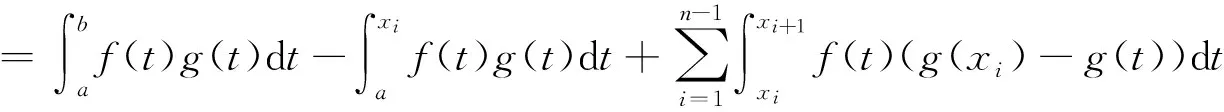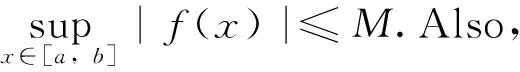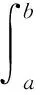Proving the Second Mean Value Theorem for Riemann Integrals by Riemann-Stieltjes Integrals
(School of Management, Yangtze University,Hubei Jingzhou 434023)
Xiang Changlin (School of Information and Mathematics, Yangtze University, Hubei Jingzhou 434023)
1 Introduction
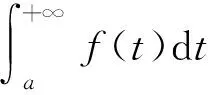
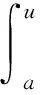
In many textbooks such as 《Mathematical Analysis》[1]and 《Principles fo Mathematical Analysis》[2], the key ingredient in the proof of Theorem 1 is the second mean value theorem for Riemann integrals, which is stated as follows.
Theorem2Letfbe a Riemann integrable function on [a,b] andgbe a monotone function.Then, there existsξ∈[a,b] such that:
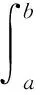
However, in standard textbooks[1], the proof of Theorem 2 is quite technical and complicated, which prevents readers from the essential of the proof.Motivated by making the proof more transparent, it is devoted in this paper to find a new and simple proof for Theorem 2.It turns out that the integrating by parts formula of Riemann-Stieltjes integrals provides a useful tool.By making use of this approach, a new proof is given for the second mean value theorem for Riemann integrals.Also, a new proof for Theorem 1 can be given by the same approach.
The integrating by parts formula for Riemann-Stieltjes integrals reads as follows.
Proposition1Letfbe a Riemann integrable function on [a,b] andgbe a monotonic function.Then:
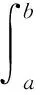
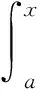
This formula should be known to experts in this area.However, since we do not find a reference, we will give a direct proof.Further researches on the second mean value theorem for Riemann integrals can be found in [3,4] and the references therein.
In the following sections, we first give the definition of Riemann-Stieltjes integrals.Through acknowledging Proposition 1, Theorem 2 is proved.We also use this proposition to give a new proof for Theorem 1.Finally, in the last section,Proposition 1 is proved.All notations in this paper are standard.
2 Riemann-Stieltjes Integrals
In this section, the Riemann-Stieltjes integral on the bounded interval [a,b] is introduced briefly.
Letg:[a,b]→Rbe a nondecreasing function.LetT:a=x0 For any functionfon [a,b], define the Riemann-Stieltjes sums as: for anyξi∈Δi=[xi-1,xi].If there existsJ∈Rfor anyε>0, there existsδ>0 such that: holds wheneverξi∈Δiand ‖T‖<δ, then we say thatfis Riemann-Stieltjes integrable on [a,b] with respect tog(w.r.t.g, in short), and it’s denoted as follows: Similar to the notations of Riemann integral, we can regard the Riemann-Stieltjes integral as: Ifh:[a,b]→Ris nonincreasing, it’s defined as follows: In this way, a Riemann-Stieltjes integral of a function is defined on [a,b] w.r.t.any monotone function on the same interval. Lemma1(Properties of Riemann-Stieltjes integral) Letgbeanondecreasing function on [a,b].Then, (iii) Iffis continuous on [a,b], thenfis Riemann-Stieltjes integrable w.r.t.g. In this section,Theorem 2 is proven by making use of Proposition 1 first, and then some further applications of Proposition 1 are given. According to the text book《Mathematical Analysis》[1], it suffices to assume thatgisanonnegative nonincreasing function and to prove that there existsξ∈[a,b] as follows: (1) Sincegis monotone, using Proposition 1 yields: Applying the property (ii) of Lemma 1 and noting thatgis nonincreasing,it’s found that: Thus, using the nonnegativity ofg,the following is derived: ≥g(b)F(b)-m(g(b)-g(a))≥mg(a) That is: Hence, using the first mean value theorem of Riemann integrals, pointξ∈[a,b] is obtained,such that: This proves (1) and thus finishes the proof. As a further application of the above method, the Dirichlet theorem is proven for improper Riemann integrals without using the second mean value theorem of Riemann integrals. LetFbe defined as in the statement of the theorem.For anyu1>u2>a, Proposition 1 gives: SinceFis bounded andg(t)→0 ast→+∞, we have: (2) Also, sinceFis bounded, there existsM>0 such that |F(t)|≤M.Hence: (3) Combining (2) and (3) yields: LetT:a==x0 A rearranged argument gives: Note that: Hence: (4) It’s claimed that: (5) (6) which implies (5).The claim is proved. It’s also noted that when ‖T‖→0, we havex1→a.Hence: (7) (8) Therefore, by sending ‖T‖→0 on both sides of (4) and combining (5)、(7)、(8),the following is obtained: The proof is complete. [1]Department of Mathematics,East China Normal University.Mathematical Analysis[M].3rd Edition.Beijing:Higher Education Press,1999. [2] Rudin W.Principles of Mathematical Analysis[M].3rd Edition.McGraw-Hill Book Co., 1976. [3] Zhang F P,Jin C Y.Proof of the Extended Second Mean Value Theorem[J].Journal of Henan University, 2012, 42(3): 227~229. [4]Liu R C,Song G L.Proof the Second Mean Value Theorem by Intermediate Value Theorem[J].Journal of Daqing Petroleum Institute, 2008, 32(6): 112~114.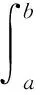
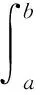

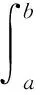
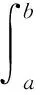
3 Proof of Theorem 2 and Further Applications of Proposition 1
3.1 Proof of Theorem 2
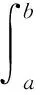





3.2 Proof of Theorem 1
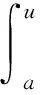
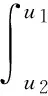
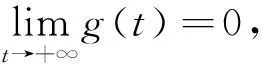
4 Proof of Proposition 1