基于相關(guān)性的超聲合成孔徑成像信號(hào)相位校正

王濤，羅林（通信作者），彭朝勇，高曉蓉，葉彩群

（西南交通大學(xué)物理科學(xué)與技術(shù)學(xué)院無(wú)損檢測(cè)研究中心，四川成都，610031）

1 相位校正原理

采用超聲合成孔徑成像技術(shù)，通過(guò)單發(fā)多收方式采集數(shù)據(jù)。AFMC為全矩陣采集得到的信號(hào)，為一個(gè)三位數(shù)組。其中，每一個(gè)矩陣單元都包含了一組A掃數(shù)據(jù)ATi,Rj(t),即Ti發(fā)射，Rj接受的間相關(guān)信號(hào)。可用AFMC(T,R,t)表示TR接發(fā)組A掃信號(hào)中t時(shí)刻的信號(hào)幅值信息。

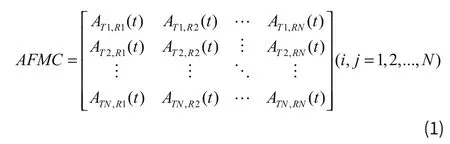
對(duì)成像區(qū)域進(jìn)行離散化處理。設(shè)P為聚焦點(diǎn)，晶片Ti發(fā)射超聲波被點(diǎn)P反射后，被晶片Rj。整個(gè)過(guò)程的時(shí)間為：

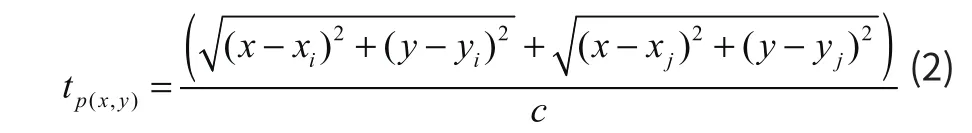
其中，已知xi表示Ti和Tj陣元中心點(diǎn)。當(dāng)tp(x,z)已知，即可得到全矩陣數(shù)據(jù)矩陣中每個(gè)A掃信號(hào)在P點(diǎn)的幅值信息。對(duì)三維數(shù)據(jù)矩陣AFMC內(nèi)所有A掃信號(hào)在P點(diǎn)的幅值信息進(jìn)行疊加，得到全聚焦幅值。

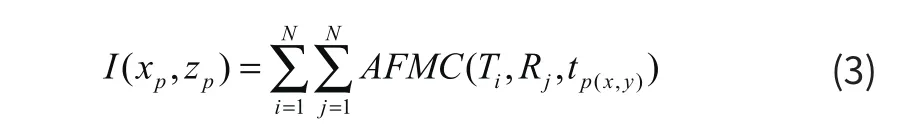
然后我們可以求出待檢測(cè)區(qū)域內(nèi)每一網(wǎng)格點(diǎn)處的全聚焦超聲幅值，再對(duì)所得到的值進(jìn)行成像。

而對(duì)參考信號(hào)來(lái)說(shuō)，Sn(t)和Sn+1(t)之為兩個(gè)相鄰A掃信號(hào)中待計(jì)算相關(guān)性部分，互相關(guān)函數(shù)Cn(t)為：

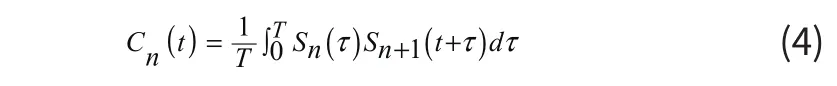
其中T為周期。

在相關(guān)校正中，采用互相關(guān)函數(shù)的離散形式來(lái)計(jì)算延時(shí)參量：

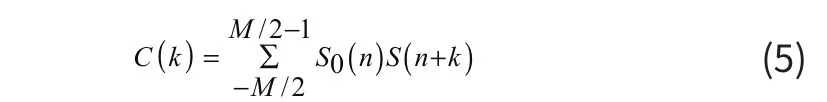
式中S0(n)是標(biāo)準(zhǔn)A掃信號(hào)，S(n+k)是相對(duì)S0來(lái)說(shuō)的待校正信號(hào),k為采樣點(diǎn)序號(hào)。M是位于反射點(diǎn)位置兩邊的采樣點(diǎn)數(shù)，取20～30為最佳。為了得到延時(shí)估計(jì)值，需要計(jì)算出兩列信號(hào)互相關(guān)函數(shù)C(k)最大值。然后，基于鄰近互相關(guān)系數(shù)得到相位誤差，平移校正。

為準(zhǔn)確找到最大的相關(guān)系數(shù)Cmax(k0)，即該信號(hào)相對(duì)參考信號(hào)的相位差(時(shí)間位置差)Δtj=k0，需要先確定k0的最佳值，為此需要選擇最佳相差拾取公式。由此構(gòu)造函數(shù)：

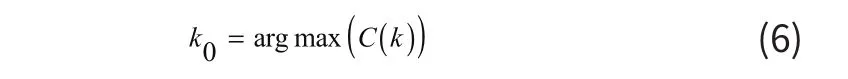
其中C(k)表示相差k步的兩相鄰信號(hào)修正后所得的互相關(guān)系數(shù)，參數(shù)k0是Cmax(k0)取最大值C(k)時(shí)的變量。當(dāng)k=k0時(shí)兩列相鄰信號(hào)的互相關(guān)系數(shù)為C(k)最大值Cmax(k0)。

根據(jù)相位差Δtj，所有子孔徑中任意i通道的延時(shí)差可由下式計(jì)算：

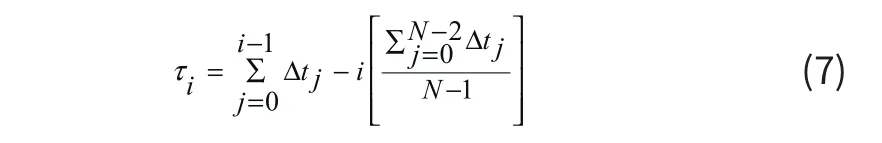
其中，當(dāng)i=0時(shí)，τi=0。在實(shí)際實(shí)驗(yàn)中需要對(duì)所有信道只一次進(jìn)行校正。

因在非均勻情況下，線性部分和非線性部分并存，直接忽略線性部分有可能導(dǎo)致校正后信號(hào)之間的互相關(guān)系數(shù)不如校正保留線性部分的結(jié)果。因此將式(7)右邊分割成三個(gè)部分：

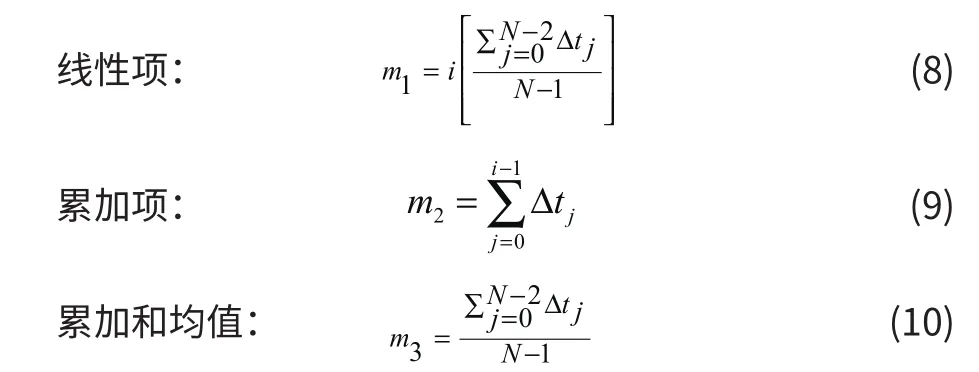
利用如上的三個(gè)部分可組合得到三種相差拾取公式：

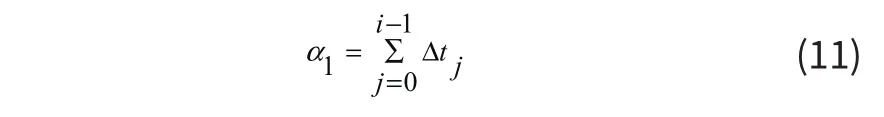
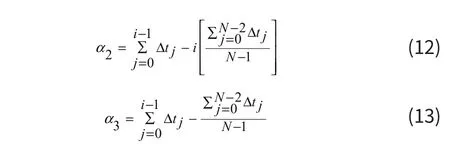
為尋找最佳的自變量(即最佳相差拾取公式的選擇)，構(gòu)造函數(shù)：

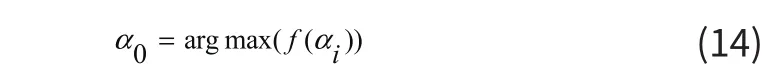
其中f(αi)表示消除相位差αi(i=1,2,3…)后得到各信號(hào)序列之間的互相關(guān)系數(shù)。其中α0為使得argmax(f(αi))取得最大值所對(duì)應(yīng)的變量。當(dāng)αi=α0時(shí)各個(gè)信號(hào)相干疊加效果最強(qiáng)，由此得到最合適的相位校正差量。校正后的信號(hào)表示為：

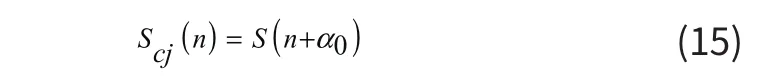
對(duì)校正后信號(hào)進(jìn)行(3)式處理得到相位校正超聲圖像。

2 結(jié)果與分析

先對(duì)處于同一深度的兩個(gè)缺陷點(diǎn)進(jìn)行全聚焦超聲成像仿真，并加入隨機(jī)相位畸變，以隨機(jī)相位屏模擬波前畸變相位，產(chǎn)生系統(tǒng)的非均勻性噪聲。

用濾波函數(shù)對(duì)一個(gè)空間不相關(guān)的正態(tài)分布隨機(jī)函數(shù)進(jìn)行濾波，由此得到相位連續(xù)分布的非均勻介質(zhì)相位屏Φ(x)。所構(gòu)造的濾波函數(shù)為滿足kolmogonov隨機(jī)過(guò)程的功率譜FΦ(k)。信號(hào)的綜合延時(shí)量ti(i=1,2,3…,N)（其中N為陣元數(shù)目）為一組隨機(jī)序列，可以統(tǒng)計(jì)規(guī)律受到戒指非均勻性影響的結(jié)果。

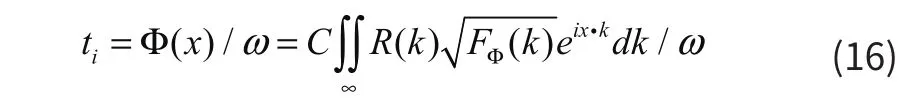
其中，符合kolmogonov分布的功率譜為：

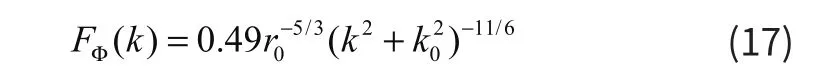
式r0表示戒指非均勻性，k為波數(shù)，R(k)是均值為零、單位方差的Hermitian 復(fù)Gaussian隨機(jī)過(guò)程，C為調(diào)節(jié)常數(shù)（可控制相位屏的方差）。該式表示接收信號(hào)和相位差之間所滿足的統(tǒng)計(jì)規(guī)律。對(duì)所接受的A掃信號(hào)加入相應(yīng)的隨機(jī)延時(shí)。

■ 2.1 仿真

表1是Field Ⅱ的對(duì)在同樣深度下的兩缺陷點(diǎn)進(jìn)行仿真的結(jié)果。

表1 仿真參數(shù)

?

圖1為仿真兩個(gè)缺陷點(diǎn)得到的結(jié)果，包括無(wú)相位差及有相位差的兩點(diǎn)成像、相差校正后的兩點(diǎn)成像。

圖1 兩點(diǎn)缺陷仿真結(jié)果

為了比較四幅圖像，分別計(jì)算其橫向分辨率，結(jié)果如表2所示。

表2 兩點(diǎn)仿真圖像橫向分辨率

由定義已知橫向分辨率值越小，橫向分辨力越高，經(jīng)相差校正后的圖像橫向分辨率值略大于無(wú)相差圖像的橫向分辨率值，明顯小于相差校正前的圖像橫向分辨率值，因此可說(shuō)明相位校正方法能夠提高對(duì)于兩個(gè)缺陷點(diǎn)的橫向分辨力，且改進(jìn)的自適應(yīng)校正相差方法對(duì)圖像橫向分辨力的提高程度優(yōu)于自適應(yīng)校正相差方法。

■2.2 實(shí)驗(yàn)

實(shí)驗(yàn)設(shè)備為Multi2000Pocket多路便攜式超聲實(shí)驗(yàn)系統(tǒng)、奧林巴斯超聲探頭以及標(biāo)準(zhǔn)試塊CSK-IA進(jìn)行試驗(yàn)。主要參數(shù)如表3所示。

設(shè)定參數(shù)后，先進(jìn)行全矩陣捕獲采集數(shù)據(jù)，然后對(duì)數(shù)據(jù)進(jìn)行全聚焦成像處理。因標(biāo)準(zhǔn)試塊因其結(jié)構(gòu)特性所造成的相位畸變相對(duì)較小,如圖2所示。其中圖2 (a)是由全矩陣A掃信號(hào)離散化結(jié)果，圖2(b)是單獨(dú)一列A掃信號(hào)。

表3 參數(shù)設(shè)置

圖2 采集的原始信53F7

有無(wú)相差的單點(diǎn)全聚焦成像結(jié)果如圖3(a)和圖3(b)。

對(duì)加入相位屏后得到的數(shù)據(jù)進(jìn)行全聚焦成像，結(jié)果如圖3(b)和圖4 (b)。利用原始自適應(yīng)校正技術(shù)對(duì)信號(hào)進(jìn)行處理再全聚焦成像結(jié)果如圖3(c)和圖4(c)所示。而改進(jìn)后的自適應(yīng)處理技術(shù)對(duì)信號(hào)優(yōu)較好的校正，全聚焦成像如圖3(d)和圖4(d)。

計(jì)算其橫向分辨率及峰值信噪比來(lái)反應(yīng)兩種校正方法的對(duì)比。結(jié)果如表4、表5所示。

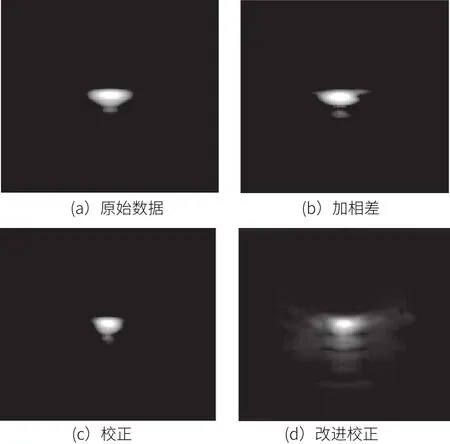
圖3 單點(diǎn)成像

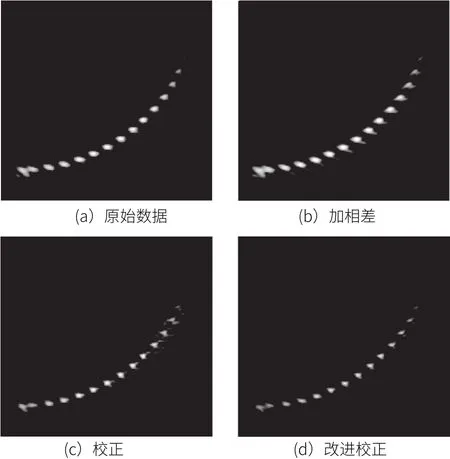
圖4 多點(diǎn)成像

表4 橫向分辨率

從表4可以看出，不論是單點(diǎn)缺陷還是多點(diǎn)缺陷，兩種校正方法對(duì)缺陷點(diǎn)的橫向分辨率都有所提高，而改進(jìn)后的校正方法提升程度最高。

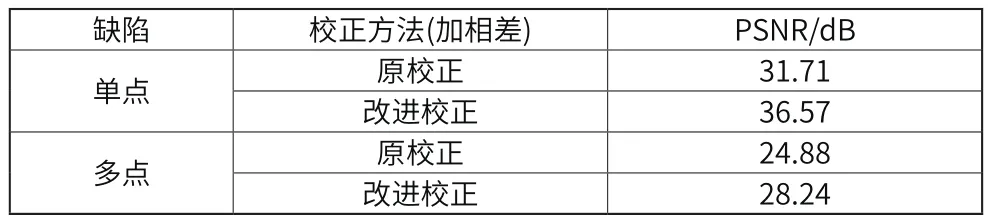
表5 峰值信噪比(PSNR)

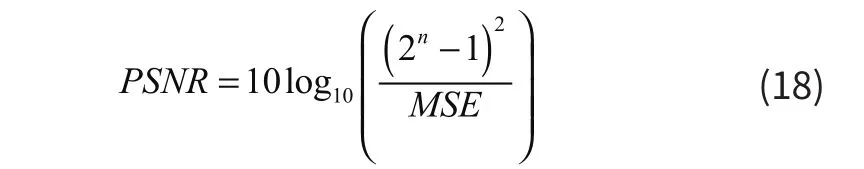
式中n是每個(gè)采樣值的比特?cái)?shù)，MSE是原圖像與被處理圖像之間的均方誤差。

從表5中可以看出，單點(diǎn)和多點(diǎn)缺陷的成像結(jié)果表明兩種相位校正方法均能提升峰值信噪比，從而改善超聲圖像提高檢測(cè)結(jié)果，但改進(jìn)后的校正方法明顯優(yōu)于原始校正。

3 結(jié)論

針對(duì)超聲成技術(shù)中，非均勻介質(zhì)和檢測(cè)表面不平整造成的原始相位相干校正技術(shù)的不足，采用全聚焦技術(shù)并結(jié)合自適應(yīng)校正技術(shù)，通過(guò)計(jì)算A掃信號(hào)之間的相關(guān)性，考慮線性誤差、非線性誤差及其疊加項(xiàng)對(duì)相位校正的影響，優(yōu)化相位偏差的估計(jì)并進(jìn)行校正。實(shí)驗(yàn)結(jié)果表明，該方法在仿真模擬和實(shí)際實(shí)驗(yàn)上，都可以提高相位校正能力，使得圖像的橫向分辨率、峰值信噪比相對(duì)原始技術(shù)都有所提高，得到的結(jié)果可以有效的反應(yīng)缺陷的特征信息。

* [1] Holmes C, Drinkwater B W, Wilcox P D. Post—processing of the full matrix of ultrasonic transmit–receive array data for non—destructive evaluation[J]. Ndt & E International, 2005,38(8):701—711.

* [2] Tasinkevych Y, Trots I, Nowicki A, et al. Modified synthetic transmit aperture algorithm for ultrasound imaging[J]. Ultraso nics, 2012, 52(2): 333—342.

* [3]杜英華.合成孔徑聚焦超聲成像技術(shù)研究[D].天津大學(xué),2010.