基于預處理的點到點最短路徑計算方法

陸文琦，谷遠利，李萌，王碩，張源

(北京交通大學城市交通復雜系統理論與技術教育部重點實驗室，北京 100044)

隨著計算機和地理信息技術的快速發展，智能導航與位置查詢服務在輔助人們出行方面發揮出越來越重要的作用，尤其是車載導航系統正逐漸成為所有駕駛人員的必備產品。但是由于城市汽車保有量的不斷攀升，道路網絡規模不斷增大，交通情況愈發復雜，用戶急需更加高效、準確的最短路徑算法以獲取動態靈活的導航服務。

最短路徑算法被廣泛應用于車輛誘導、交通流分配等領域，最早用來解決點到點最短路徑的算法是經典Dijkstra算法[1]，Bellman-Ford算法和Floyd算法也被用來解決過此類問題。Hart等[2-3]在經典Dijkstra算法基礎上提出了A*算法，該算法利用當前點到目標點的最短路徑長度的估值更快地向目標點靠近，始終根據既定的規則，通過不斷擴大“最有希望”[4]的節點集合進行探索，由于在搜索過程中省略大量無謂的搜索路徑，比Dijkstra算法的效率更高。與A*算法類似，Pearl等[5]提出了Weight A*算法(簡稱WA*)，在計算路徑時，A*算法和WA*算法均以兩點間直線距離作為最短路徑長度估值，WA*求解得到的路徑質量與其算法運行時設置的參數有關，可以在大規模網絡上找到一條與標準最短路徑相差不大的路徑。

以上算法主要以標號法為主，沒有對圖進行預處理。針對大規模網絡計算時間長、占用內存空間大、無法應對快速查詢的缺陷，在傳統算法的基礎上逐步形成了基于預處理的最短路徑算法，包括預處理階段和路徑查詢階段[4]。例如，在A*算法的基礎上，Goldberg等[6]提出了基于預處理的ALT算法，由A*、Landmark和Triangle inequality方法組合而成。此外，與經典單向Dijkstra算法相對應，雙向Dijkstra算法可以以源點和終點為圓心同時向外搜索，加快了搜索效率，并且雙向算法可以與其他方法相結合形成新的算法，解決點到點最短路徑問題。Goldberg等[7]將雙向算法和A*算法、ALT算法結合，并且通過添加快捷弧的預處理方法，使查詢效率極大提升。其他常用的預處理方法有層次化法，包括分割法[8]、層次公路HH算法[9]、HNR算法[10]、THR算法[11]等等。

本文在reach剪枝算法的基礎上，詳細介紹了reach的計算方法，包括reach精確值和上界值，對兩種reach計算方法在不同規模路網上進行對比，并將基于reach的剪枝算法與雙向Dijkstra算法結合形成了RE算法，利用EFSS數據結構[12-13]建立了包含路段阻抗和交叉口轉向延誤的交通路網，通過算例和幾種不同規模的交通路網測試了RE算法，驗證其適用性和算法效率。

1 算法原理及實現

1.1 雙向Dijkstra算法

雙向Dijkstra算法即從搜索的源點s和終點t交替使用Dijkstra算法，直到兩端點都找到了到達同一節點的最短路徑。在節點數量較多的圖上，應用雙向Dijkstra算法能大幅減少搜索時間。該算法用df(v)和dr(v)分別記錄正向和反向算法中節點v至源點s和終點t的距離，用μ記錄最短路徑長度。算法的基本步驟如下：

步驟1：初始化，對于所有節點v，df(v)=∞，dr(v)=∞，μ=∞；

步驟2：交替使用正向和反向算法，在正向搜索時，若遇到某一被反向搜索作為永久標號點的節點w時，若滿足μ>df(v) +l(v,w) +dr(w)，則更新μ；反向搜索時同理進行更新；

步驟3：判斷是否滿足終止條件，若滿足則輸出最短路徑，不滿足則返回步驟2。

雙向Dijkstra算法的終止條件[5]有兩種設置方式，其中一種是正向搜索每前進一步，判斷搜索是否滿足終止條件，同理反向搜索每前進一步，也判斷是否滿足終止條件；另一種是完成一個完整正反向搜索后進行終止條件判斷，本文選擇后者作為終止條件的設置方式。雙向Dijkstra算法與單向Dijkstra算法的技術對比見表1。

表1 雙向Dijkstra算法與單向Dijkstra算法技術對比Table 1 Technical comparison of bidirectional algorithm and one-way Dijkstra algorithm

1.2 基于reach的預處理方法

1.2.1 相關定義

假定一條由s到t的路徑P，并且點v在路徑P上，如圖1所示。

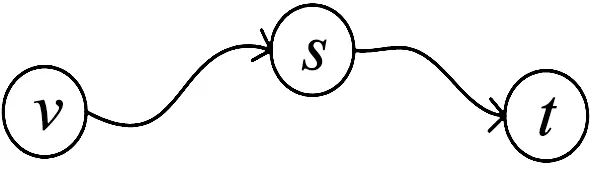
圖1 reach的定義Fig.1 Definition of reach

reach(v,P)代表節點v關于最短路徑P的reach，其準確值是s到v的子路徑長度和v到t的子路徑長度中的最小值。

reach(v,P)=min{dist(s,v),dist(t,v)}。

(1)

那么v關于整個圖的reach由r(v)表示。

r(v)=max{reach(v,P)}。

(2)

基于reach的預處理方法又稱為reach剪枝算法，是指在預處理階段計算出所有節點的reach值，再根據相應的條件在查詢過程中刪剪掉不滿足條件的節點。

1.2.2 reach值的計算

計算reach值的基本方法是由Gutman等[14]提出，而后Goldberg等[7]提出了改進算法。根據相關研究[7,14]，求解reach精確值的效率不高，基于reach剪枝主要用reach上界值(reach bound)來代替精確值，由此產生了許多計算reach上界值的方法，下文分別介紹reach精確值和一種常用的reach上界值的計算方法。

reach精確值的計算過程為：初始化，對于所有節點r(v)=0，對于每一個節點x，生成一個根節點在x的完整最短路徑樹Tx，對于樹上每一個節點v，計算出v到根節點x的距離(depth[v])和v到距離自身最遠的子節點v*的距離(height[v])，由(3)計算得出v在以x為根的最短路徑樹上的reach的值，記為rx(v)。

rx(v)=min{depth[v],height[v]}。

(3)

若rx(v) >r(v)，則令rx(v) =r(v)，最后得到的r(v)是reach的精確值，計算過程如圖2所示。

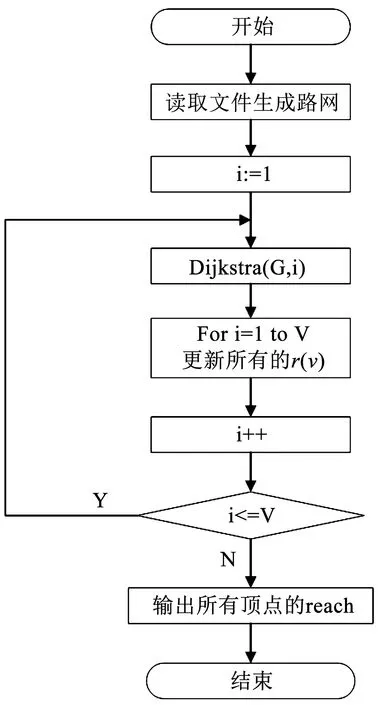
圖2 reach精確值計算流程圖Fig.2 Flow diagram of calculating exact reach

計算reach上界值的基本過程為：

步驟1：以每個節點x為根節點按照一定條件生成部分最短路徑樹；

步驟2：計算部分最短路徑樹上某些節點的reach的上界值和reach的精確值；

步驟3：根據得到的精確的r(v)，對圖進行收縮修改，保存刪除后的圖；

步驟4：不斷重復步驟1、2、3，不斷更新相關節點reach的上界值，直到所有的上界值都被計算出來。

reach上界值與reach精確值相比，其優勢在于引入了生成部分樹(partial tree)的概念，計算reach精確值時每次都要生成完整的最短路徑樹，在小網絡中，每條完整最短路徑樹的長度不會很長，但是在上百乃至上千個節點的大網絡中，生成完整最短路徑樹就會消耗大量的時間，而reach上界值算法采用必要條件[7]終止樹的生成，在更新隊列和計算上界值時節約了時間。因此，在小規模網絡中，優先采用reach的精確值算法，而在中等以及大規模網絡上，優先采用reach的上界值算法。

1.3 RE算法

1.3.1 算法原理

通常情況下，若一個節點在一條很長的最短路徑的中間，那么這個節點的reach值應該是一個很大的數，直觀上來看，如果在運行雙向Dijkstra算法時處理某一個節點，該節點的reach值太小以至于不能到達目標終點的情況下，可以忽略該點，將其從正向隊列和反向隊列中刪除，從而提高效率，這是RE算法的一般原理。

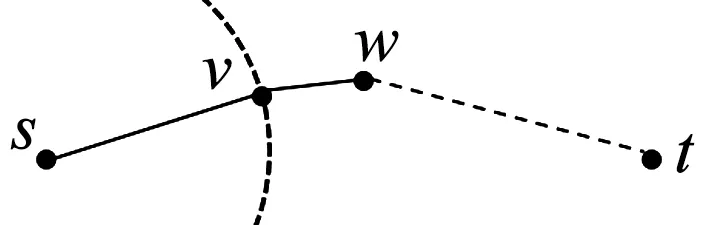
圖3 RE算法原理Fig.3 Principe of RE algorithm

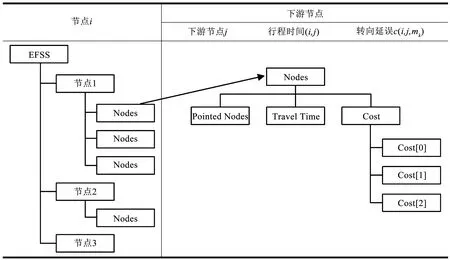
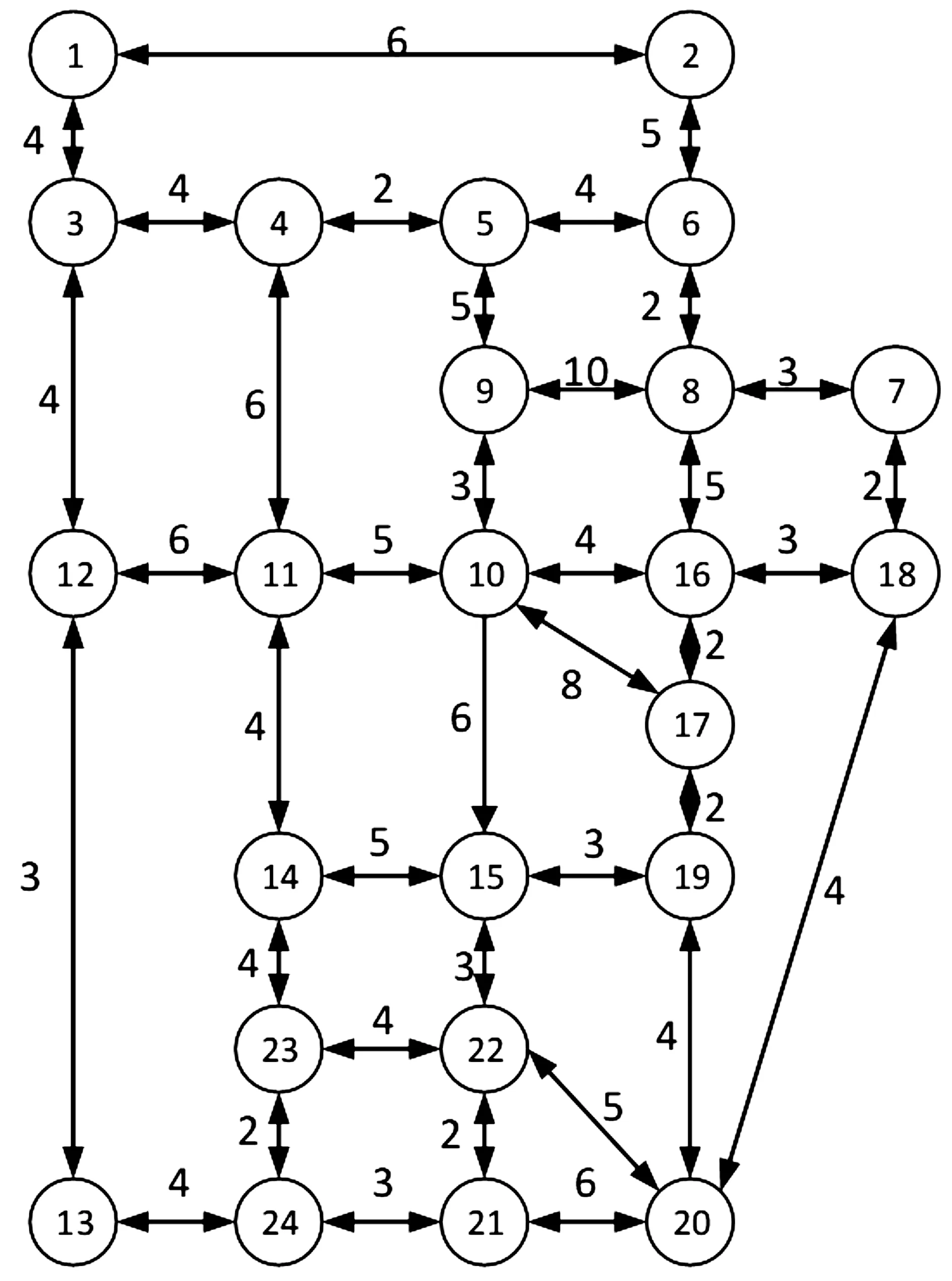
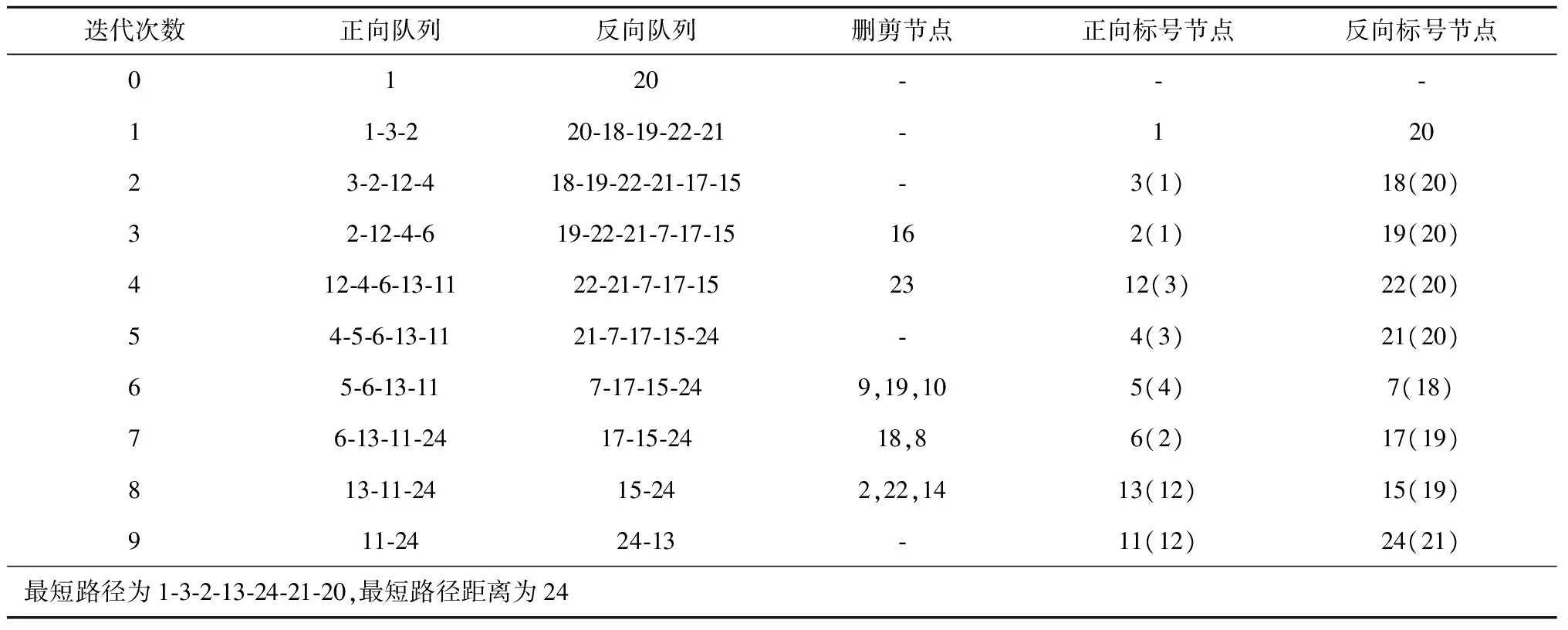
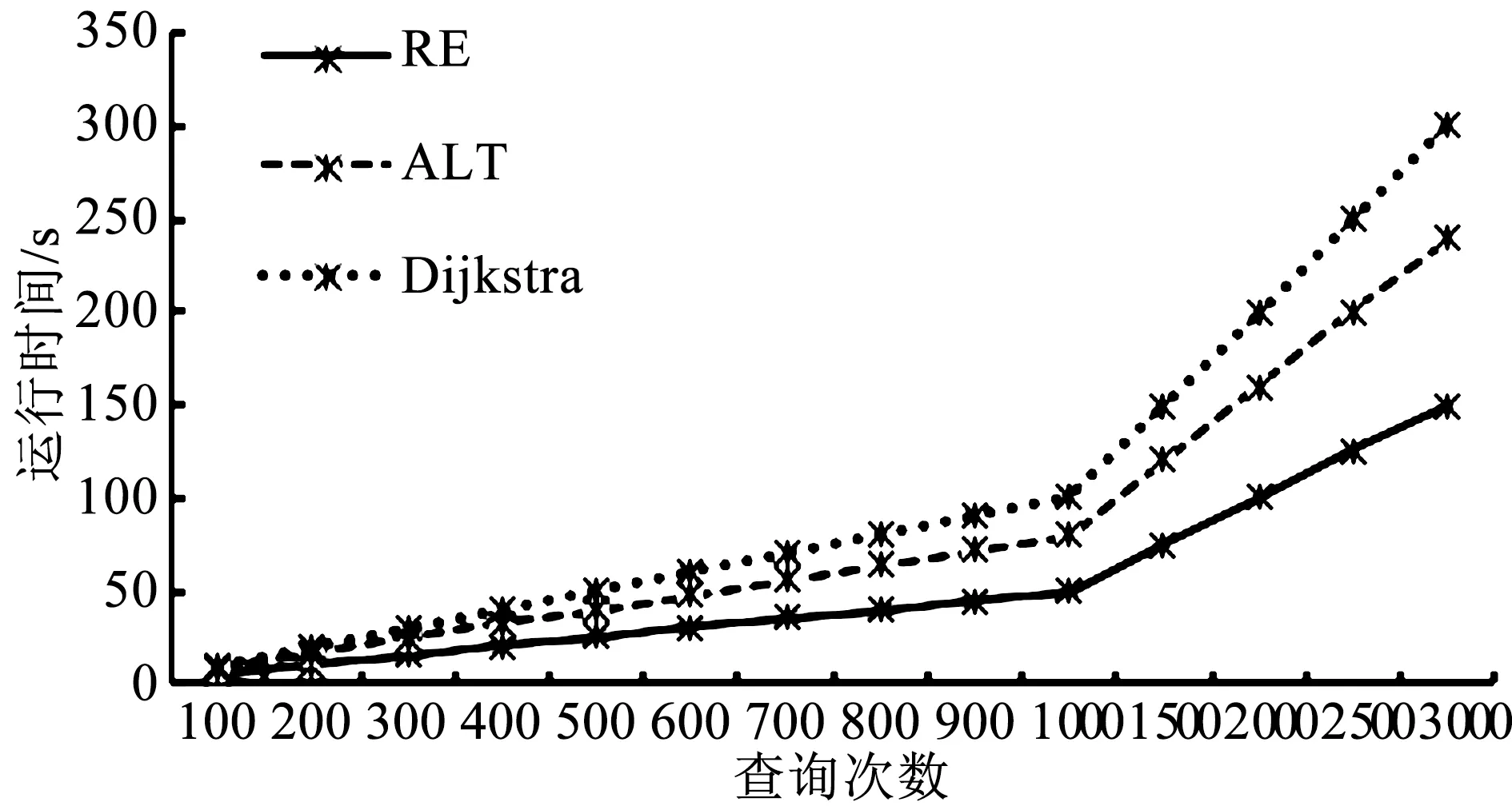
r(w)

(4)

r(w)

(5)

具體刪剪方法如圖3所示，在一條由s到t的路徑上，w為當前需要處理的節點，r(w)為節點w的reach值，如果同時滿足公式(4)和公式(5)，則將節點w刪剪掉，使其不再進入優先隊列(priority queue)中，減少搜索過程中隊列的節點個數。

1.3.2 算法步驟

假設，在一般路網上，兩節點間的路段是雙向的并且具有阻抗，首先通過預處理得到rf(v)和rr(v)，分別記錄前向鏈表和反向鏈表計算的reach精確值或上界值，結構體df[V]和dr[V]記錄兩個方向Dijkstra算法每個節點的編號(ID)、標號距離(label)以及是否成為永久標號點(scaned)，結構體df[V]和dr[V]分別放入兩個優先隊列(priority queue)中按標號距離由小到大自動更新排列。Ωf、Ωr分別作為在正向、反向搜索中一個被標記節點的最小距離標記，即正向隊列(forward_q)和反向隊列(reverse_q)隊首元素的標號距離，prune(v)記錄節點是否被刪剪，μ1和μ2分別記錄正向和反向搜索得到的臨時最短路徑值，具體RE算法以雙向Dijkstra算法為基礎，以下是RE算法在該假設下的迭代過程：

步驟1：初始化所有變量，把起點s和終點t放入正向優先隊列和反向優先隊列；

步驟2：使用正向Dijkstra算法，當處理節點v時，若scanned_r[v]=false、rf(v)

步驟3：使用反向Dijkstra算法，當處理節點v時，若scanned_f[v]=false、rr(v)

步驟4：μ=min{μ1,μ2}；

步驟5：判斷是否滿足終止條件Ωf+Ωr≤μ，若滿足，輸出最短路徑和距離，否則返回步驟2繼續迭代。

2 算法測試

2.1 交通網絡構建

將RE算法應用于車載導航路徑優化需要構建交通網絡，由于實際道路網絡是有條件限制的網絡[15]，比如交通管理手段帶來的交叉口禁止轉向限制，不同流向車輛之間的干擾和信號控制手段產生的交叉口轉向延誤等等，為了更好地描述這一問題，本文引入擴展的前向星形結構(extend forward star structure，EFSS)來組建交通網絡。

EFSS是在文獻[12-13]中提到的一種較為經典的限制網絡表示方法，是一種如圖4所示的鏈表結構，在原有的星形鏈表基礎之上加以擴展，加入了對交叉口轉向延誤的存儲，并方便檢索。該結構能有效存儲交叉口之間的路段阻抗以及交叉口的交通延誤，與傳統的采用鄰接矩陣建立路網拓撲關系相比，EFSS數據結構節省了大量的內存空間，便于預處理和查詢搜索。

圖4 EFSS數據結構Fig.4 EFSS data structure

2.2 結果分析

本文為使用小規模網絡蘇福爾斯網絡來對RE算法的準確性進行驗證，利用EFSS數據結構搭建了如圖5所示的交通網絡，為方便顯示預處理以及刪剪節點的過程，該路網設置交叉口轉向延誤時間為0，兩節點間的路段不考慮道路方向不均勻系數的影響，即道路兩個方向的阻抗相同，目標是查找節點1到節點20的最短路徑距離，首先通過預處理，可以獲得如表2所示的每個節點的reach值，預處理時間為16 s。

表2 蘇福爾斯測試網絡預處理結果Table 2 Results of preprocessing on Sioux Falls test network

圖5 蘇福爾斯測試網絡算例Fig.5 Example of Sioux Falls test network

利用RE算法求解節點1到節點20的最短路徑的迭代過程如表3所示。

表3 RE算法求解最短路徑迭代過程Table 3 Iterative process for solving the shortest path by RE algorithm

在此算例中，RE算法共完成更新節點18次，在迭代過程中刪剪節點10個。用經典Dijkstra算法求解該算例需要更新節點28次，而且需要完成對全部節點的搜索，造成了運算時間和運算空間的浪費。RE算法保證了計算結果的準確性。為了驗證RE算法的效率，利用蘇福爾斯測試路網隨機生成若干對查詢節點，選擇Dijkstra、ALT和RE算法進行查詢，如圖6所示，結果表明在小規模路網上，RE算法效率略高于Dijkstra算法和ALT算法。

圖6 相同路網下不同算法效率對比Fig.6 Comparison of the efficiency of different algorithms on the same network

為檢驗新算法在實際交通應用中的適用性，需要在大規模路網上進行測試，本文利用EFSS數據結構建立了5個不同規模的交通網絡，利用隨機數生成交叉口延誤數據與道路阻抗模擬實際路況，并在各個路網上隨機生成1 000對節點，用Dijkstra算法、ALT算法和RE算法分別進行查詢，并且計算出平均查詢時間，得到如表4所示的數據。

表4 不同規模路網上3種算法平均查詢時間Table 4 Comparison of average running time of three algorithms on networks of various scales

通過在各種規模的網絡中運行RE算法可以發現，路網規模越大，節點數量越多，RE算法的性能越好，在查詢速度上的優勢越明顯。在大規模網絡上，RE算法與Dijkstra相比運算效率提升了90% 以上，與ALT算法相比提升了65%，所以RE算法更加適用于大規模的路網，并且隨著reach預處理技術的不斷改進，算法效率可以得到進一步提高。因此，RE算法在車載導航系統中可以發揮路徑規劃的作用，也可用于物流配送線路優化等實際問題，具有良好的適用性和應用前景。

3 結語

本文在經典的最短路徑Dijkstra算法的基礎上，將雙向Dijkstra算法與基于reach的預處理方法相結合形成RE算法，針對RE算法預處理階段計算reach精確值效率不高，時間較長的問題，引入reach的上界值算法來取代reach的精確值進行計算。本文分析了RE算法的一般步驟，并且利用EFSS鏈表結構建立了考慮交叉口延誤和路段阻抗的交通網絡，測試RE算法的性能，將其與Dijkstra算法和ALT算法進行對比。實驗結果表明，RE算法在不同規模網絡上較Dijkstra算法和ALT算法相比有一定的優勢，并且隨著網絡規模的不斷擴大，RE算法其優勢也逐步擴大，體現出該算法較好的適用性。

本研究將重點放在算法實現和路網預處理問題上，還有可以優化和深入探討的部分，比如在構建路網數據時，考慮的道路阻抗與交叉口延誤取值為靜態值，沒有體現路網的動態性，在后續的研究中，考慮引入路段行程時間函數與交叉口的轉向懲罰函數，并豐富和完善動態網絡加載中的RE最短路徑搜索算法，使算法能更準確地描述真實交通狀況。

參考文獻：

[1]DIJKSTRA E W.A note on two problems in connection with graphs [J].Numerical Mathematics,1959,1(1)：269-271.

[2]HART P E,NILSSON N J,RAPHAEL B.A formal basis for the heuristic determination of minimum cost paths [J].IEEE Transactions on System Science and Cybernetics,1968,4(2):100-107.

[3]DORAN J E.An approach to automatic problem-solving [EB/OL].[2017-03-02].https://aitopics.org/search? view=&filters=&sort=score+desc&q=An+approach+to+automatic+problem+solving+.

[4]付強.基于預處理的交通網最短路徑實時查詢研究[D].合肥：中國科學技術大學,2015.

[5]PEARL J.Heuristics: Intelligent search strategies for computer problem solving[M].MA,US： Addison-Wesley Pub.Co.,Inc.,1984.

[6]GOLDBERG A V,HARRELSON C.Computing the shortest path: A search meets graph theory [M]// Proceedings of the sixteenth annual ACM-SIAM symposium on discrete algorithms.Philadelphia,PA,USA: Society for Industrial and Applied Mathematics,2005:156-165.

[7]GOLDBERG A V,KAPLAN H,WERNECK R F.Reach for A*: efficient point-to-point shortest path algorithms [EB/OL].[2017-03-12].http://epubs.siam.org/doi/abs/10.1137/1.9781611972863.13.

[8]SANDERS P,SCHULTES D.Highway hierarchies hasten exact shortest path queries [EB/OL].[2017-03-04].https://link.springer.com/chapter/10.1007/11561071_51.

[9]GEISBERGER R,SANDERS P,SCHULTES D,et al.Contraction hierarchies: Faster and simpler hierarchical routing in road networks[C]// International Workshop on Experimental Algorithms.Provincetown,MA,USA: [s.n.],2008: 319-333．

[10]SCHULTES D,SANDERS P.Dynamic highway-node routing[M]// Proceedings of 6th International Workshop on Experimental Algorithms.Berlin: Springer,2007: 66-79.

[11]BAST H,FUNKE S,MATIJEVIC D,et al.In transit to constant time shortest path queries in road networks[EB/OL].[2017-03-12].http://dx.doi.org/10.1137/1.9781611972870.5.

[12]ZILIASKOPOULOS A K,MAHMASSANI H S.Time dependent shortest path algorithm for real time intelligent vehicle highway system applications [J].Transportation Research Board，1993(1408)：94-100．

[13]ZILIASKOPOULOS A K,MAHMASSANI H S.A note on least time path computation considering delays and prohibitions for intersection movements [J].Transportation Research Part B Methodological,1996,30(5):359-367.

[14]GUTMAN R J.Reach-based routing: A new approach to shortest path algorithms optimized for road networks[C]// Proceedings of the Sixth Workshop on Algorithm Engineering & Experiments & the First Workshop on Analytic Algorithmics & Combinatorics.New Orleans,LA,USA: [s.n.],2004: 100-111.

[15]杜牧青,程琳.考慮交叉口轉向延誤的最短路徑拍賣算法[J].西南交通大學學報,2010,45(2):249-254.