一種民機顫振模型配重設計優化方法
張蘇華 /
(上海飛機設計研究院,上海201210)
0 引言
顫振是彈性結構在氣流中發生的一種不穩定現象[1]。顫振本質上是一種自激振動,是彈性機體與氣動力、慣性力三者耦合造成的結果。當飛機以從小到大的速度飛行時,隨著阻尼作用的減弱,擾動造成的機體結構振動會由衰減變為發散,這種發散現象即為顫振[2]。研究顫振現象及機體結構的顫振特性對于確立飛機的飛行包線具有重要意義,中國民航總局頒布的CCAR25.629條款對此有詳細的規定[3]。顫振研究的目的是通過分析、試驗等手段確定機體結構的臨界顫振速度、顫振頻率以及參與顫振耦合的結構模態分支,并考察相關結構參數對于機體結構顫振特性的影響[4]。機體結構的顫振特性研究是飛機防顫振設計的重要內容。目前,機體結構的顫振特性研究主要分為數值分析和模型試驗兩種途徑。
一般地,顫振模型與飛機的動力學特性近似,需要在外形、剛度、質量等參數上對飛機參數進行縮比模擬[5]。由于跨音速顫振模型具有體積小、結構質量占比高、慣量占比小的特點,其配重設計一直是民機高速顫振模型領域的一個難點。本文針對現有民機跨音速顫振模型配重設計環節中的質量、慣量拆分工程做法提出了一種優化方法,具體為依據模型剛軸方向建立拆分點,對被拆分質量點的質量、慣量進行線性拆分,并將該方法同時運用到模型的目標總重及結構質量計算中。上述方法提高了顫振模型質量、慣量拆分精度,同時解決了傳統工程處理方法在模型展向重心位置配平不夠精確的問題。該方法在某民機垂尾高速顫振模型適航驗證試驗項目中進行了實踐運用,取得了良好的效果。
1 經驗公式
在民機顫振模型配重設計過程中,處理模型的目標總重和結構質量時會使用質量、慣量合并或質量、慣量拆分的方法。質量、慣量合并的方法較為成熟,一般基于移軸定理[6]推導得到,不屬于本文討論范疇,但其公式對于質量、慣量拆分具有參考意義,式(1)為質量、慣量合并公式。
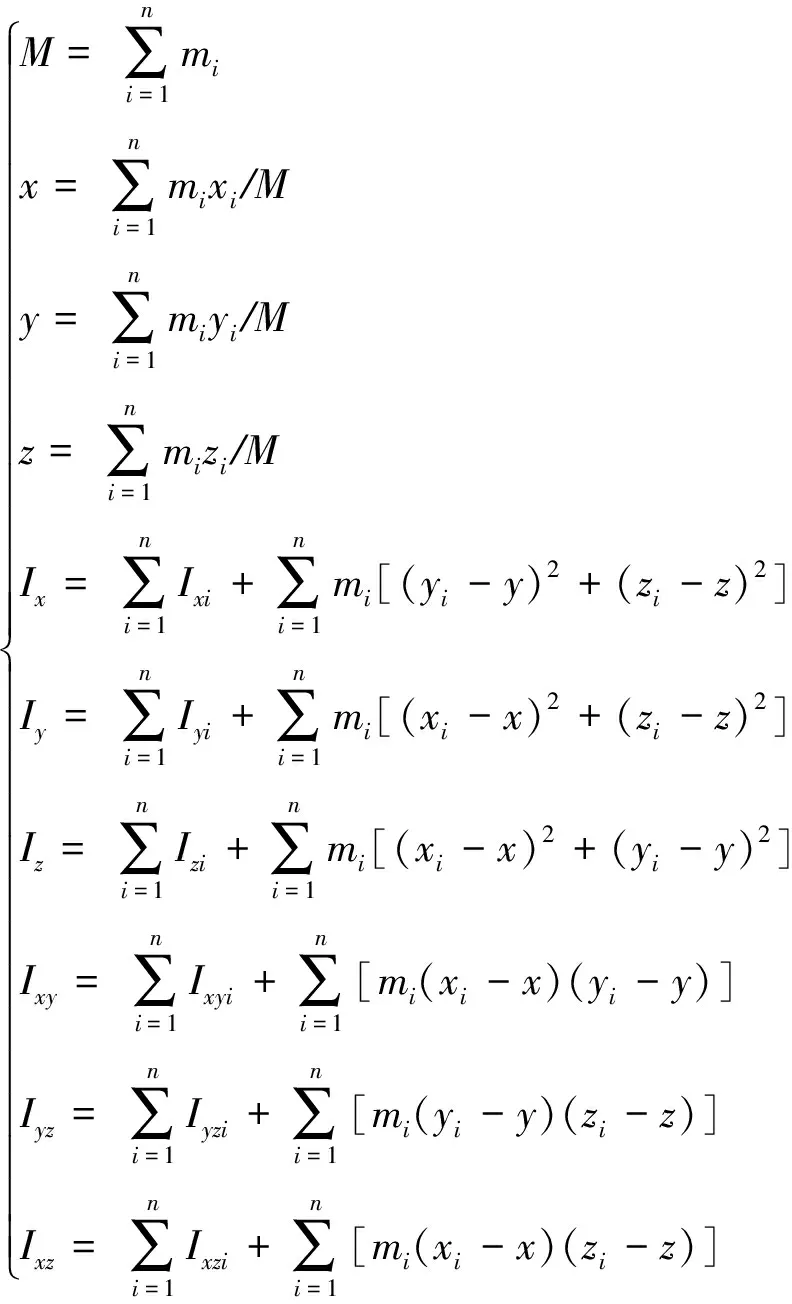
其中,mi為待合并質量點質量;xi,yi,zi為待合并質量點坐標;Ixi,Iyi,Izi為待合并質量點的繞軸慣量;Ixyi,Iyzi,Ixzi為待合并質量點的質量慣性積;M為合并質量點的質量;x,y,z為合并質量點的坐標;Ix,Iy,Iz為合并質量點的繞軸慣量;Ixy,Ixz,Iyz為合并質量點的質量慣性積。
質量、慣量拆分的過程與質量、慣量合并的過程相反,其目的是試圖使用兩個或多個假想的拆分質量點來等效替代被拆分質量點(集中質量點)。對于民機跨音速顫振模型配重設計,工程上定義質量點質量、慣量的拆分計算在相鄰肋板間進行,即將一個待拆分質量點在相鄰兩肋板間拆分為兩個拆分質量點,如圖1所示。
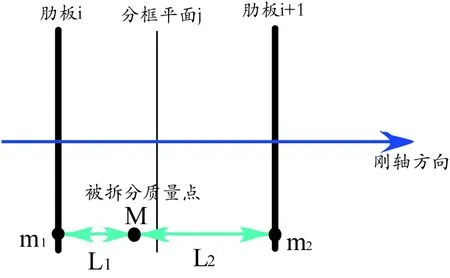
圖1 質量點質量、慣量的拆分示意圖
工程上近似認為拆分點的質量、慣量拆分結果與該待拆分質量點到相鄰兩個肋板的距離成反比。反向推導質量、慣量合并公式得到質量點質量、慣量的拆分公式見式(2)。
(2)
其中,M為待拆分點的質量;Iz,Iu(u=x,y)為待拆分質量點的繞軸慣量;It(t=xy,yz,xz)為待拆分質量點的質量慣性積;mi為拆分點的質量;Izi,Iui(u=x,y)為待拆分質量點的繞軸慣量;Iti(t=xy,yz,xz)為待拆分質量點的質量慣性積。
2 現狀及問題
在進行民用飛機顫振模型配重設計時,集中質量點質量、慣量拆分的目標是將肋板間的待拆分質量點的質量、慣量拆分到位于肋板平面的拆分點上。一般地,肋板是相互平行且與剛軸(z軸)垂直的,某型民機多個顫振模型配重設計依據該質量、慣量拆分方法得到了較好的試驗結果。
近年來,隨著研制工作的深入,肋板不平行(見圖2)、肋板與剛軸不垂直(見圖3)的情況多次出現。考慮到空間中的質量點繞軸慣量,其計算公式見式(3):
Iz(e)=Iz(s)+m(x2+y2)
(3)
其中,m為該質量點質量;x,y為該質量點坐標;Iz(s)為質量點繞自身軸系慣量;Iz(e)為質量點繞剛軸慣量。依據式(3),在兩個拆分點x,y坐標不對應相同的情況下,這些拆分點必有一部分繞軸慣量與x,y坐標有關,而與式(2)中工程定義的拆分比例pi無關的。不考慮該部分繞軸慣量,繼續沿用距離定義式(2)中的拆分比例pi拆分繞軸慣量的工程方法是不夠嚴密的。需要發展一種新的工程假設或提出一種新的理論公式,并經過多輪試驗驗證,滿足新條件下的目標質量、慣量拆分需要。
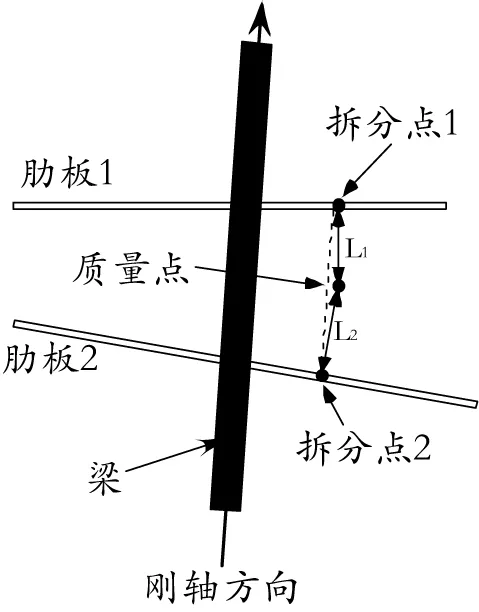
圖2 肋板不平行情況示意圖
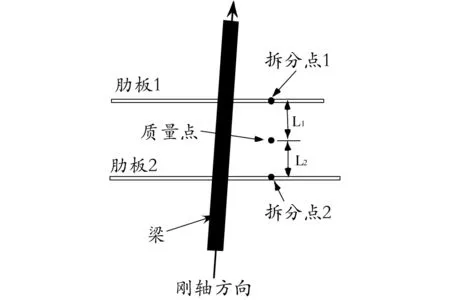
圖3 肋板與剛軸不垂直情況示意圖
另外,在某型民機多個顫振模型設計項目中,經常發現模型制造狀態實際展向方向重心位置與理論展向方向重心位置存在偏差。雖然分析發現,此類偏差對于試驗結果不造成不可控影響,但為了更精細地模擬飛機的質量狀態,需要發展一種新的工程方法消除此類重心位置偏差,并經過多輪試驗驗證。
3 改進的工程方法
針對第2節中所述的肋板不平行或肋板與剛軸方向不垂直的情況,本文基于傳統工程方法發展了一種基于剛軸方向的模型質量、慣量線性拆分方法。即將跨音速顫振模型設計的剛軸方向確立為模型質量、慣量拆分方向,重新定義拆分點及式(2)中的L1、L2,而后基于剛軸方向對模型的質量、慣量進行線性拆分。具體實施過程如圖4、圖5所示,先過被拆分質量點作剛軸方向平行線,該平行線與該被拆分質量點相鄰兩肋板平面得到兩個交點,定義這兩個交點為拆分點,其與被拆分質量點相應的矢量距離即為L1、L2。
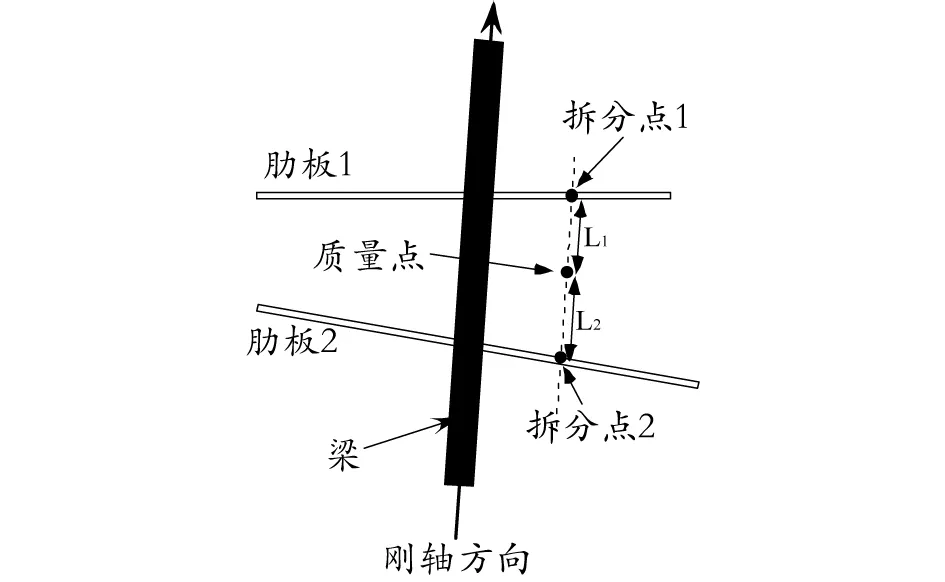
圖4 改進方法在肋板不平行情況中的運用
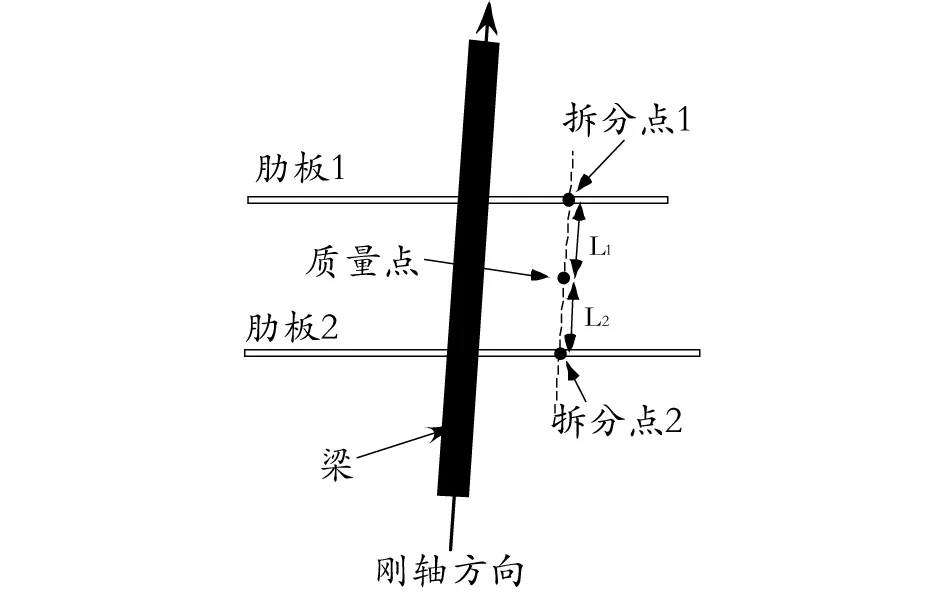
圖5 改進方法在肋板與剛軸不垂直情況中的運用
按上述改進方法實施后,若定義剛軸方向為z軸,則被拆分點與拆分點的x、y坐標相同,通過式(3)可以發現,上述方法解決了傳統工程方法在肋板不平行、肋板不與剛軸垂直情況下由于拆分點x、y坐標不同造成的繞軸慣量拆分的問題,同時減少了工程實踐中式(2)的計算量。
針對2節中關于模型實際重心與理論重心存在偏差的問題,本文提出了一種基于上述改進的質量、慣量拆分方法的新型工程計算流程,具體如圖6所示。
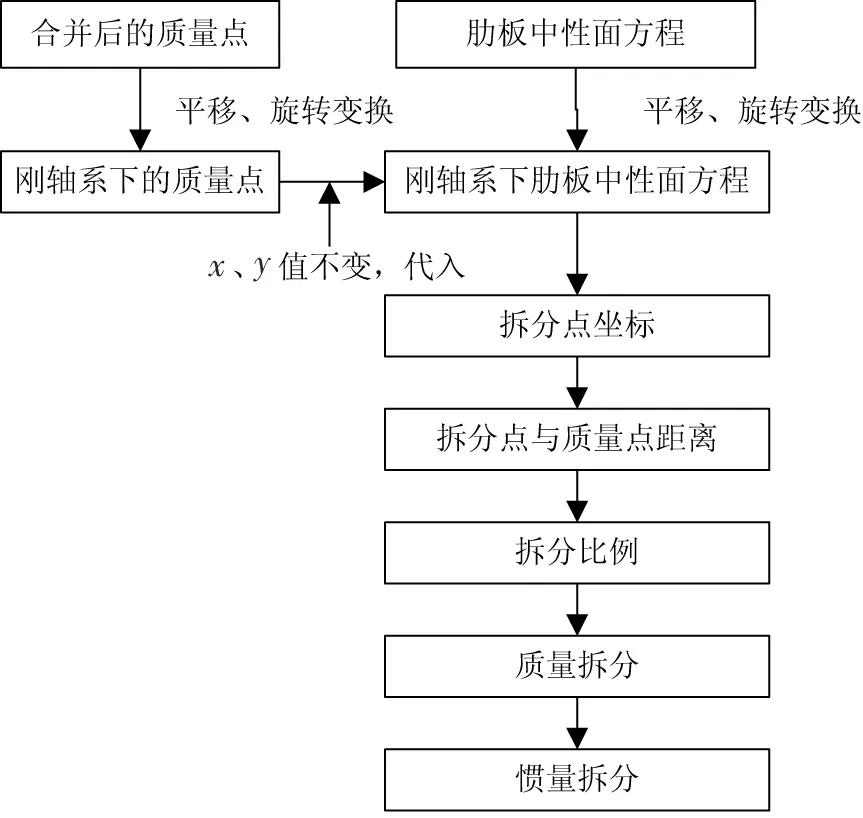
圖6 基于改進方法的質量、慣量拆分計算流程
在以往的工程實踐中,與圖6類似的流程僅在計算模型目標總重時運用,而在處理模型結構質量時過分依賴結構拆分平面的精度,未曾考慮對模型結構質量進行拆分,現在增加模型框架結構質量、慣量的拆分流程,作為對以往工程方法的一種改進,如圖7所示。
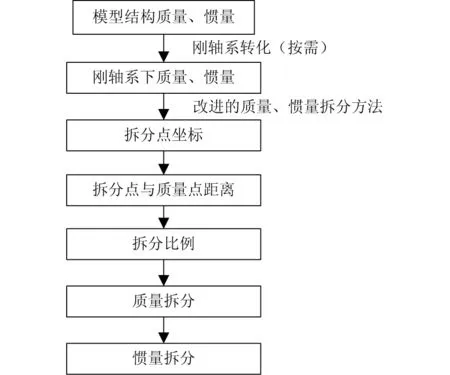
圖7 新增模型結構質量、慣量特性的拆分流程
對于改進后的模型結構質量、慣量狀態,其重心及慣量特性是基于肋板平面計算的,而目標總重的重心及慣量特性計算也基于肋板平面,這就實現了配重設計完全在肋板平面進行,解決了以往工程做法在模型展向配平方面欠考慮的問題,實現了模型在展向方向的重心位置配平。
3 工程實踐
該方法在某民機垂尾高速顫振模型設計項目中進行了運用,模型配重設計結果示意如圖8所示,其配重設計部分數據見表1。
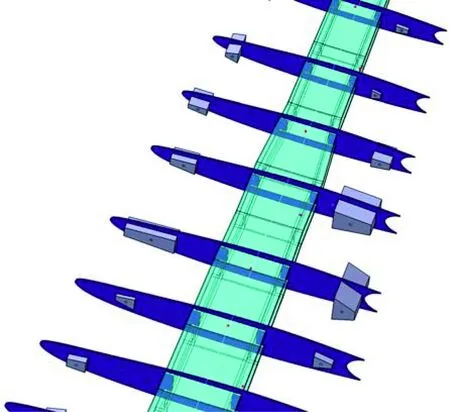
圖8 某型民機垂尾高速顫振模型配重設計結果示意圖
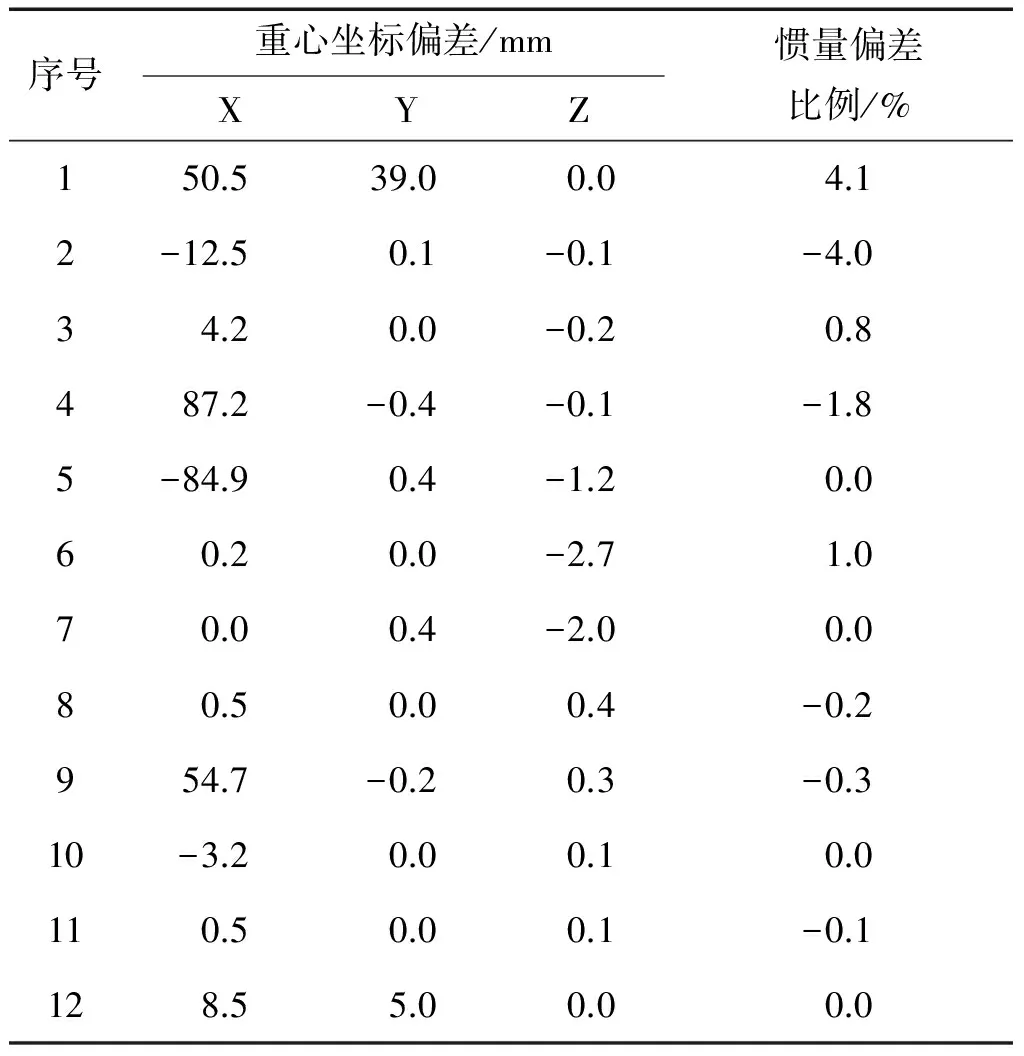
表1 某型民機垂尾高速顫振模型配重設計部分數據
分析表1可以發現,模型展向重心位置偏差較小,慣量偏差控制在±5%以內,模型配重精度滿足工程要求。
模型加工完成后,對上述顫振模型進行振動試驗,部分試驗數據見表2。
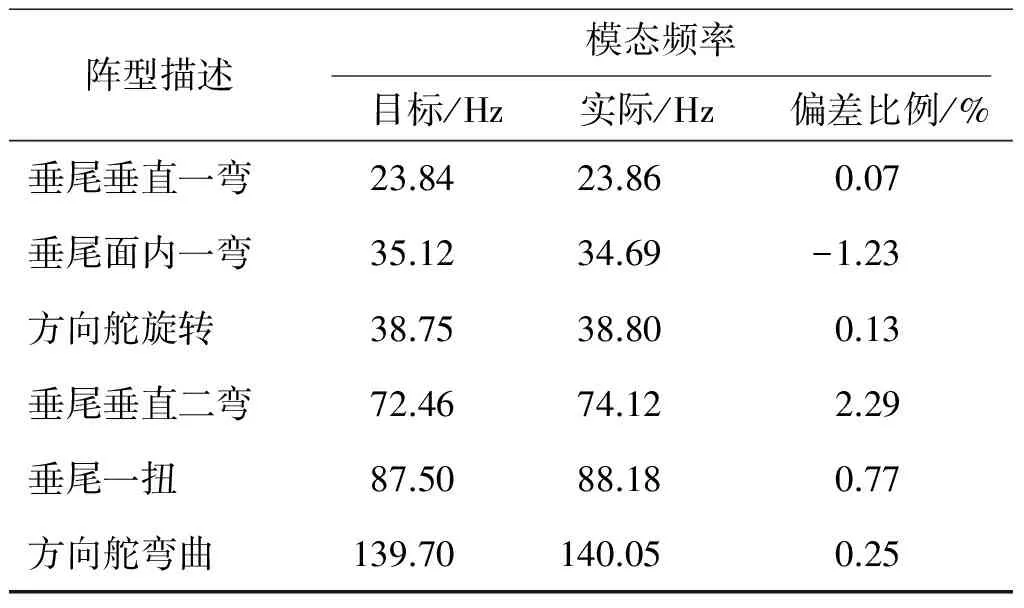
表2 某型民機垂尾高速顫振模型振動試驗部分數據
分析表2可發現,實際加工的垂尾顫振模型動力學特性與設計目標符合良好,模型的模擬精度較高,進一步表明了本文所述優化方法在實際工程運用方面是可行的。
4 結論
本文針對顫振模型配重設計工程實踐中存在的質量、慣量拆分公式運用問題及展向重心位置配平問題提出了一種基于剛軸方向的模型質量、慣量線性拆分方法,并將該方法運用到某型民機垂尾跨音速顫振模型配重設計中。試驗結果表明,本文方法配重計算精度高,展向重心位置配平效果好,可以推廣到其他顫振模型的配重設計中。
參考文獻:
[1] 楊超. 飛行器氣動彈性原理[M]. 北京: 北京航空航天大學出版社, 2011: 93.
[2] 陳桂彬,鄒叢青,楊超. 氣動彈性設計基礎[M]. 北京: 北京航空航天大學出版社,2004: 78-79.
[3] 中國民用航空局. 中國民用航空規章第25部:運輸類飛機適航標準[S]. 中國:中國民用航空局,2011: 61-62.
[4] 楊智春,張飛霆,趙令誠. 顫振系統中一個特殊的幾何縮比效應[J]. 中國科學:物理學 力學 天文學,2014,44(3): 293-298.
[5] 管德. 氣動彈性試驗[M]. 北京: 北京航空學院出版社,1986: 107-108.
[6] 任文敏,陳艷秋,范欽珊. 材料力學[M]. 北京: 清華大學出版社,2003: 91-94.

