改進橢圓曲線密碼體制在SET協議中的應用①

盧聞捷

(浙江理工大學 信息學院,杭州 310018)

安全電子交易協議(Secure Electronic Transaction,SET),是一個安全的電子支付模型,它主要為了解決用戶、商家、銀行的支付交易行為. SET的出現在最大程度上幫助交易參與方提高了交易的信任度,也保證了交易信息的安全性和完整性. 參與SET一次完整流程的成員有：持卡者、商家、銀行(包括發卡行與收單行)、支付網關以及認證中心. 其中持卡人是支付卡持有者,得到了發行者的授權; 發卡行是給持卡者發行信用卡的金融機構; 商家是提供貨物或服務的經營者; 發卡行是給商家提供開設帳號的金融機構; 收單行也是一個金融機構,它是接受付款的最終端,為商家建立一個賬戶并處理支付卡授權和支付; 支付網關是金融網的安全屏障與關口,實現對支付信息從Internet到銀行內部網絡的轉換,用來處理支付功能,并對商家和持卡人進行認證; 認證中心是參與交易各方都信任的第三方中介組織,為交易過程中的成員進行身份驗證[1,2].

SET核心技術包括數字簽名、數字證書、加密算法體制等. 其中SET中的加密算法體制主要應用于支付過程中的數據交換,在一般的SET支付環境中使用的公鑰加密算法是RSA的公鑰密碼體制. 本文針對SET中的加密算法體制進行研究改進.

1 橢圓曲線加密算法

橢圓曲線加密算法(Elliptic Curve Cryptography,ECC)[3-6]是基于橢圓曲線離散對數問題的密碼體制,相對于別的算法,它的每bit安全性最高. 相比RSA密碼體系,ECC體系無論在安全性能上還是通信帶寬上都具有一定的優勢,文獻[3]中對相同安全級別下的ECC和RSA的密鑰長度和密碼長度進行了對比,結果顯示隨著對于安全性能的要求加強,RSA算法的密匙長度增加的越快,ECC比RSA的硬件要求就更低.

橢圓曲線常用的定義的有限域包括兩種：素數域GF(p)和二進制域GF(2m). 在二進制域上,元素在計算機中可實現并行的加、減、乘等操作,因此硬件實現的橢圓曲線加密系統中通常使用二進制域的橢圓曲線加密方法.GF(2m)上一個非奇異橢圓曲線E由Weierstrass公式定義的：y2+xy=x3+ax2+b. 其中a,b是GF(2m)中的元素,且b≠0. 同時曲線E包括一個無窮遠點作為曲線上點的加法單位元,用O表示. 令P1=(x1,y1),P2=(x2,y2),是E上的兩個點,且P1≠-P2,則P3=P1+P2=(x3,y3)可由下式計算：

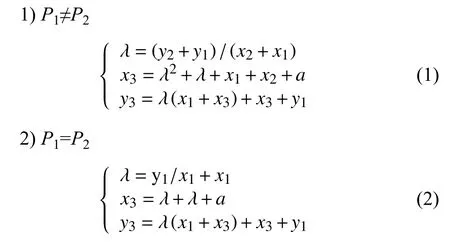
ECC的加密、解密過程,公鑰協議都要求計算橢圓曲線數乘運算.

方案流程：

首先選擇一個基域F,定義一個點P為該域上的橢圓曲線E和F上為素數階,點的坐標以(xp,yp)表示.有限域F,域元素a和b為橢圓曲線的參數,公開信息為點P和階n. 系統建立后每個使用者將會生成各自的密鑰.

1) 選取一個隨機證書d,d在區間[1,n-1]內

2) 計算點Q=dP;

3)Q為實體的公開密鑰,整數d則為實體的私鑰.

生成密鑰后的每個使用者將進行加密處理,當實體B給實體A發送一條信息M時,實體B執行步驟：

① 查找A的公開密鑰Q;

② 將信息M表示為域元素M∈Fq;

③ 選擇一個隨機整數k,k屬于區間[1,n-1];

④ 計算點(x1,y1)=kP;

⑤ 計算點(x2,y2)=kQ;

⑥ 計算c=mx2. 傳送加密數據(x1,y1,c)給A.

當實體B完成步驟后進行解密過程后,實體A解密實體B傳輸的密文(x1,y1,c),A執行步驟：

(a) 使用他的私鑰d,計算點(x2,y2)=d(x1,y1);

(b) 通過計算m=c×x2-1,解析出數據m.

上述過程中,Q=dP為公開的,若存在第三者能夠解開上述的橢圓曲線上的離散對數問題,即能從dP中求出d,就可得到解密的消息.

2 橢圓曲線數乘算法

在有限域中曲線上的兩個互異點相加,需要1次求逆,2次乘法,1次平方,9次加法(在有限域中加法的運算耗時相當少,通常略去不考慮). 由橢圓曲線密鑰交換協議可知,要提高加解密速度必須提高點的數乘的效率. ECC的加密、解密過程所要求計算的橢圓曲線數乘運算的計算如下形式：

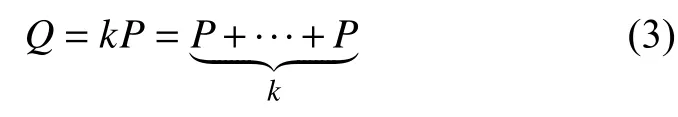
其中P為橢圓曲線上一點,k=(an-1,an-2,…,a2,a1,a0).

2.1 典型算法

該算法平均需要(m-1)次倍乘,(m-1)/2次點加,其平均計算時間復雜度是記為：t1=(m/2)A+(m-1)D.

NAF (Non-Adjacent Form)表示形式是,在二進制域橢圓曲線上,設P=(x,y),則-P=(x,x+y). 大整數k表示為通過利用得到的NAF(k)可直接計算kP. 對NAF(k)進行從左到右的掃描,根據每一位數的正負號判斷進行加或減運算. 具體過程見算法2.

NAF形式的期望權重為m/3,因而計算其平均計算時間復雜度是t2=(m/3)A+(m-1)D.

算法3的平均時間復雜度是t3=(m-1)A+(m-1)D.

結合文獻[7]的NAF算法本文給出了一個改進的NAF算法,具體見算法4.

改進算法使用隨機的帶符號二進制表示,其隨機性主要通過用011替換二進制表示的1 0. 對于不同的隨機數,帶符號的二進制表示的操作過程也有所不同.新算法不需要引入隨機變量產生的額外的計算資源,只判斷隨機數的位R是1或0,判斷發生替換字符的步驟是否發生,確保了計算速度. 其平均計算時間復雜度是t4=(m/3)A+(m-1)D.

2.2 算法比較

表1對上述算法進行了平均計算時間復雜度的比較.

表1 幾種算法的時間復雜度比較

改進的算法不僅確保了ECC的安全性,而且還具有更加優秀的平均計算時間復雜度. 另外也不需要存儲NAF碼直接進行點乘法,節省了計算資源.

3 橢圓曲線密碼體制與MD5的融合方案

提出的方案包含了應用改進的NAF編碼算法的橢圓曲線密碼體制以及MD5哈希生成算法. 在原有步驟中添加對信息M運用MD5進行128位密碼的生成.具體步驟如圖1所示,首先在進行加密過程中,將信息M在進行ECC加密的同時,進行MD5加密得到128位密碼. 傳輸過程由只發送信息M替換為發送信息M以及128位密碼. 原有加密過程不變,而在解密時,在通過ECC解密得到解密信息M后對信息M進行MD5哈希生成算法. 通過對比解密得到的128位密碼與接收到的密碼來判斷是否接受信息M.

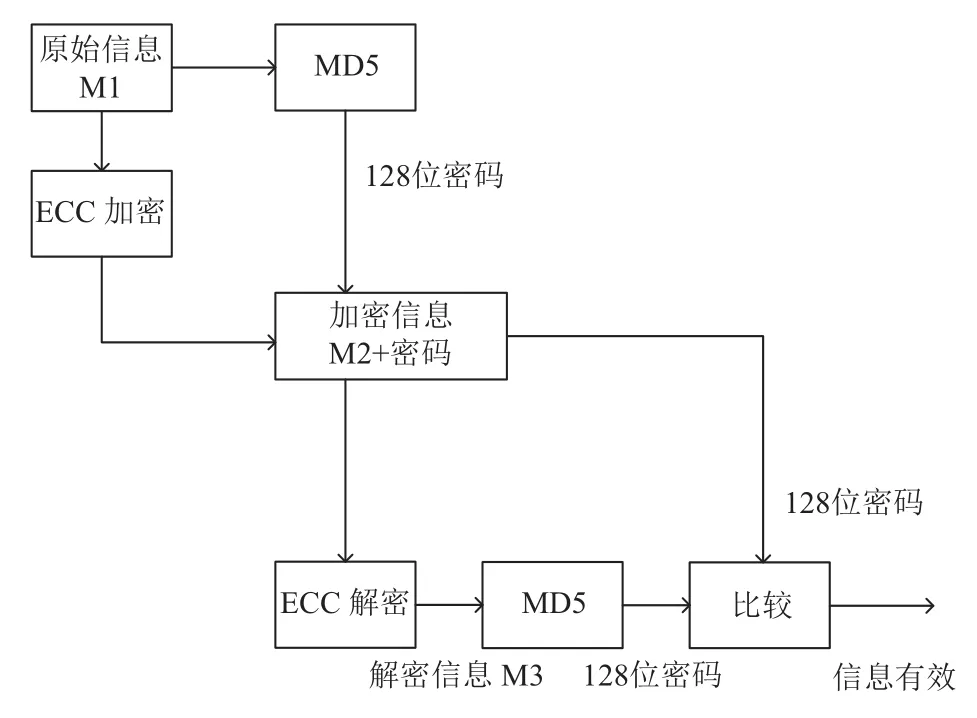
圖1 融合方案流程圖

3.1 安全性分析

改進方案通過MD5算法生成密鑰代替了原有的簡單步驟,相對原有數字簽名所使用的Hash算法,MD5進一步增強了算法的安全性. 而對于ECC的安全性,我們通過對ECC與RSA、DSA對比分析. 在目前整數因子分解技術與方法的不斷改善,計算機運行速度的提高的大環境下,RSA加解密安全保障的大整數要求日益變高,為保證安全性,就必須不斷增加RSA的密鑰長度. 目前普遍采用的安全字長為1024位以上,但密鑰長度的增加會直接導致解密速度的降低,硬件實現也越發困難. 安全性分析如表2所示. 表中MIPS表示每秒執行100萬條指令的計算機運行一年.一般認為破譯時間到達1012 MIPS年為安全. 從表中可以知道：保證安全性的情況下,ECC只需要160密鑰長度,而RSA和DSA則需要1024位. ECC的安全性遞增也大大快于RSA和DSA. 攻擊有限域上離散對數問題有指數積分法,而它對橢圓曲線上的離散對數問題并不有效. 對RSA和DSA而言,均存在指數時間算法,而對于ECC至今還沒有發現指數時間算法. 故在綜合比較下ECC的安全性更高、抗攻擊性更強.

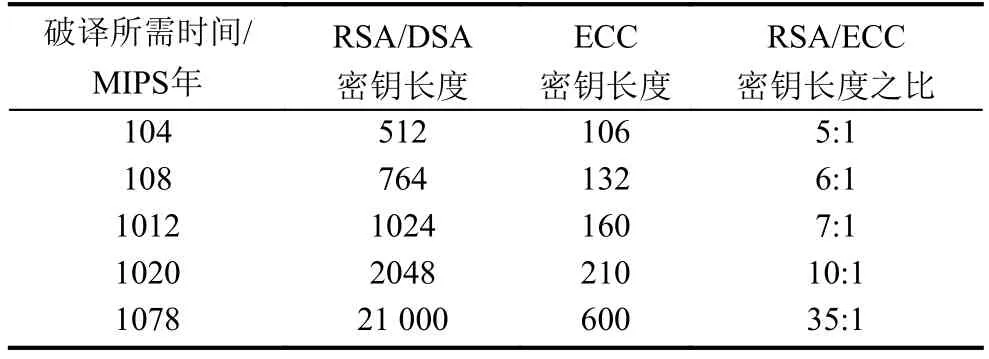
表2 破譯時間比較

3.2 融合算法性能評估

本節將對性能進行評估并列出. 對樣本文件進行隨機抽取進行加解密操作. 以增加文件大小為基礎進行不同的實驗. 表3表示了有關所有加密文件的信息,包括文件序號,存儲,時間,內存信息和所有加密文件的文件大小. 圖2以及圖3各自對表格內的內存消耗以及時間消耗給出更為直觀的展示. 其中內存消耗表示所需的處理加密算法的主內存量.

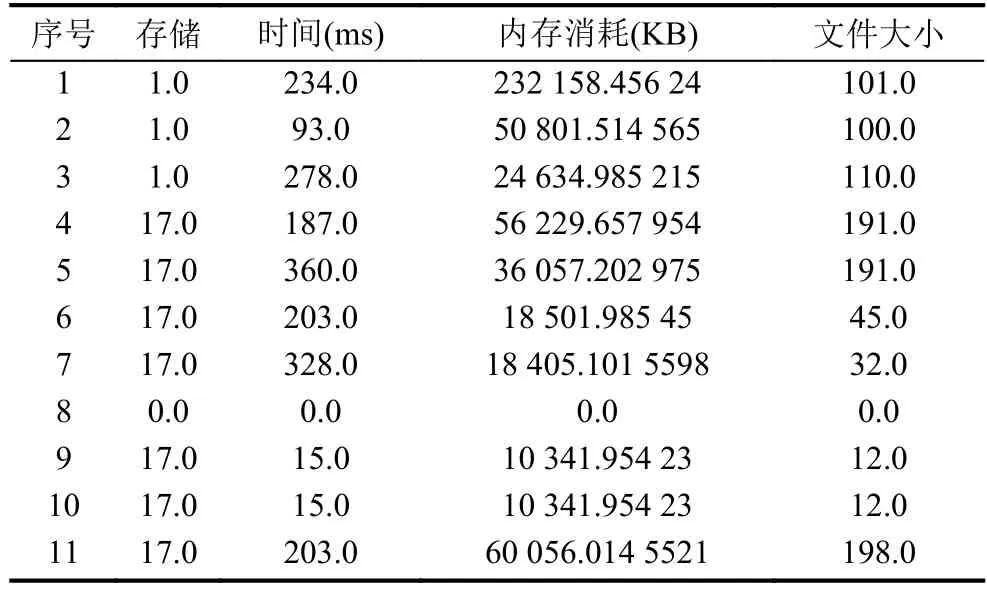
表3 文件加密時間,內存和文件大小

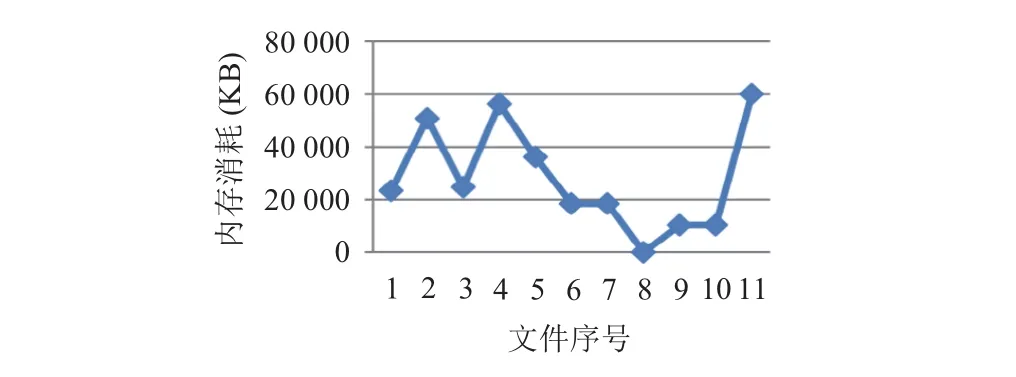
圖2 加密內存消耗

圖3 加密時間消耗

表4描述了有關所有解密文件的信息. 解密文件的準確性,時間,內存和文件大小給出的信息. 圖4對解密的內存消耗進行了展示,圖5則對于解密時間消耗給出直觀的展示. 圖6中的存儲開銷是指待加密的原始文件額外的密碼的數量. 圖7展示了數據解密的準略率,數據解密準確率是在加密文件解密之后準確恢復的數據量.

表4 文件解密時間,內存和文件大小

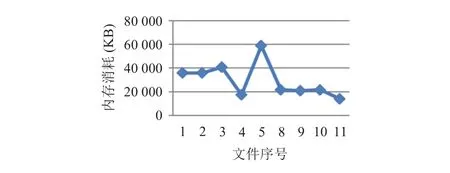
圖4 解密內存消耗

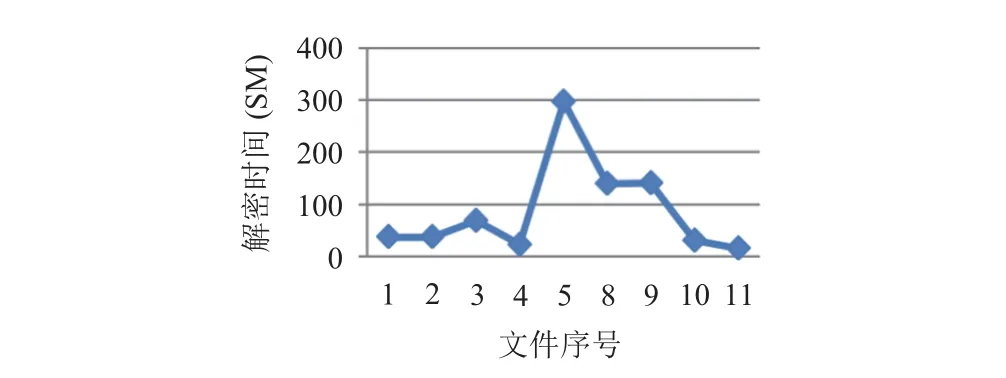
圖5 解密時間消耗

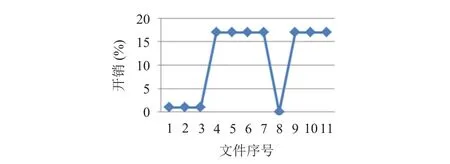
圖6 加密存儲開銷

圖7 解密準確率

分析可得加解密所消耗的時間與內存都在可接受范圍內. 由上圖分析可得：存儲開銷隨著原始文件大小增加而增加,并且總體上開銷較少. 結果表明系統在解密過程中可恢復100%的數據. 因而算法在保證安全性的同時,消耗較少的內存資源以及時間資源從而表明所提出的技術的有效性.

4 結論與展望

SET協議是電子支付系統中的關鍵,本文通過對SET協議核心技術中的加密算法體制進行研究,使用橢圓曲線算法取代目前所流行的RSA算法,從而提高了協議的安全性和工作效率. 同時本文對傳統的ECC安全算法進行了比較,使用一種改進的NAF算法. 對幾種加密算法的性能進行了評估內存消耗量和時間消耗. 同時結合了橢圓曲線密碼體制與MD5提出了改進性方案,使用MD5算法代替原有隨機生成密鑰方法. 比較證明了改進性方案消耗較少的資源并提高了安全性.

1 Lu S,Smolka SA. Model checking the secure electronic transaction (SET) protocol. Proceedings of the 7th International Symposium on Modeling,Analysis and Simulation of Computer and Telecommunication Systems.College Park,MD,USA. 1999. 358-365.

2 SetCo. SET secure electronic transaction specification：Business description. http：//www.mastercard.com/set/set.htm.1997.

3 魏來,楊朵. 一個改進的橢圓曲線密碼體制在物聯網傳輸中的研究應用. 信息技術與信息化,2015,(10)：209-212. [doi：10.3969/j.issn.1672-9528.2015.10.079]

4 Koblitz N. Elliptic curve cryptosystems. Mathematics of Computation,1987,48(177)：203-209. [doi：10.1090/S0025-5718-1987-0866109-5]

5 Miller VS. Use of elliptic curves in cryptography. Advances in Cryptology-CRYPTO’85. Santa Barbara,CA,USA. 1986.417-426.

6 Kobayashi T,Morita H,Kobayashi K,et al. Fast elliptic curve algorithm combining Frobenius map and table reference to adapt to higher characteristic. Advances in Cryptology-EUROCRYPTO’99. Prague,Czech Republic. 1999. 176-189.

7 Wang X,Wang LP,Bai YC,et al. Optimization of elliptic curve cryptography resisting power attack scalar multiplication algorithm in security system on chip. 2015 IEEE 12th International Conference on Ubiquitous Intelligence and Computing and 2015 IEEE 12th International Conference on Autonomic and Trusted Computing and 2015 IEEE 15th International Conference on Scalable Computing and Communications and its Associated Workshops (UICATC-ScalCom). Beijing,China. 2015. 1397-1401.