CT系統參數標定及成像研究

李朋飛

（華北電力大學（保定）電力工程系， 河北 保定 071000）

1 理論基礎

電子計算機斷層掃描（Computed Tomography，CT）[1]利用樣品對射線能量的吸收特性對生物組織和工程材料的樣品進行斷層成像，由此獲取樣品內部的結構信息。本文主要借助賽題中樣品的數據建立相應的數學模型，標定CT系數的參數，并據此對未知結構的樣品進行成像。根據附件一中可以確定的題中所給的橢圓模塊與圓形模塊是均勻的；附件二中接受信息的數值越大X射線的衰減程度就越大，穿過的模塊也長度越長[2]。選取介質模板半徑為4 mm的圓為研究對象，該圓心B在繞某固定點轉動時其展開的投影圖可確定為三角函數。

2 模型假設

1）X射線照射方向不變，模塊以相同的速度繞該點轉動；

2）假設X射線透射樣品在探測器上得到的投影寬度最小的時候，射線方向與橢圓長軸平行；3）假設探測器單元之間兩兩間距相同；4）假設X射線每次轉動角度相同；

5）假設X射線與正方形托盤平面絕對平行。

3 模型的建立與求解

3.1 模型一的建立與求解

根據CT投影原理可知附件二第A列至第M列、第DF列到FV列中圓形模塊投影所得數據，最大值處即圓心B的投影位置點。以第150行為基準，每一列中最大值對應行數為一個B點繞旋轉中心旋轉所的得離散點并擬合即可得出B點旋轉的正弦函數。如圖1所示：

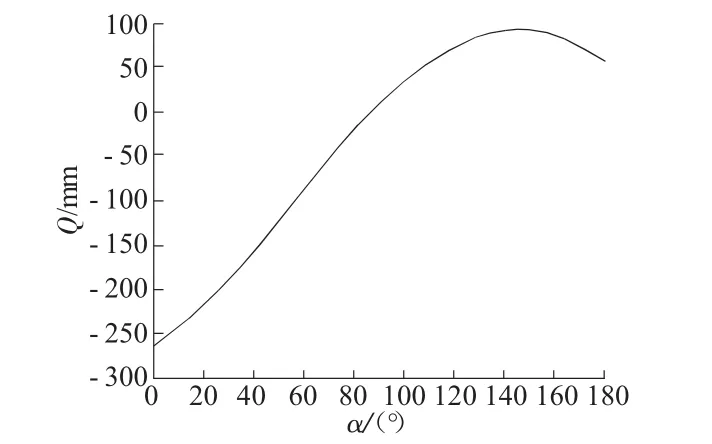
圖1 Q點旋轉所得正弦函數擬合結果

由圖1擬合結果可知B點旋轉投影函數

附件二中每一行代表一個探測器單元，每一列代表一個照射方向。選取附件二中第DF列到FV列在探測器上的投影，取出圓形模塊做對應的探測器個數，計算平均值為28.8261，那么每一探測器單元數所對應的物理寬度d=8/28.826 1=0.2775 mm。以圓形模塊圓心為基準點，根據模型分析，所擬合的正弦函數（1）的振幅即為圓點B繞旋轉中心O所成圓周的直徑，即為395.05 mm，經計算得旋轉中心與圓形模塊圓心之間的直線距離為54.813 0 mm。

將擬合圖像放入同一坐標系中最后所得結果為圖2。

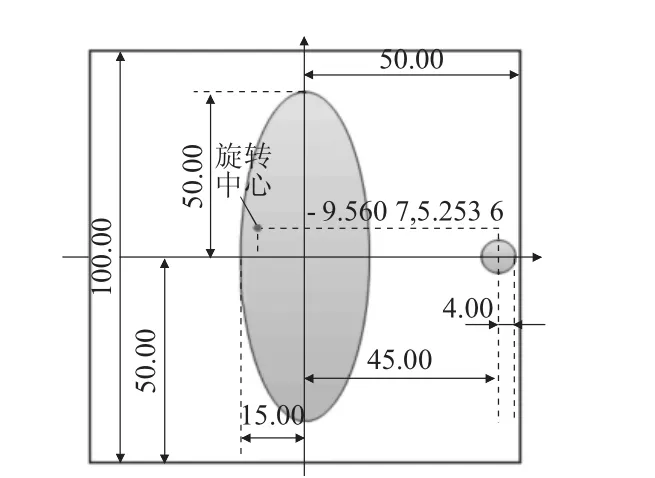
圖2 連線與水平線的夾角結果圖（mm）

以圖2中x軸正半軸為正方向建立極坐標系。X射線的180個方向分別對應該圖2中的180個離散點，由于實際情況下i為整數，所以i=149，最終方向121.082°。

3.2 模型二、三的建立與求解

利用傅里葉切片定理，所有角度下的傅里葉數據組成一個在極坐標系里的二維傅里葉變換。將極坐標系柵格化，對利用二維插值方法得到直角坐標系中對應的值求二維傅里葉逆變換，即得到目標圖像[3]。根據模型一的已知X射線的初始照射方向，根據X射線首次照射時的接收信息確定出該介質的初始相位[4]。通過傅里葉變換得到圖形的旋轉中心與托盤中求解出的旋轉中心匹配，即可確定出介質與托盤的相對位置。將附件3中的投影數據進行恢復重構，即得到附件所對應的圖像如圖3所示。

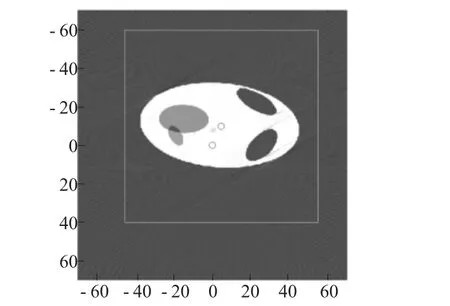
圖3 卷積濾波后的逆變換圖像

對于問題三，由射影定理[5]可知旋轉中心投影所對應的探測器單元為第256個。將其投影值置為0，在進行卷積反投影得出圖像如圖4。

圖4 旋轉中心投影置零對比圖

由此得到旋轉中心，將其以問題二類似的方法和托盤確定相對位置即可得到其位置信息，如圖5所示，其中①點為旋轉中心②點為托盤幾何中心。

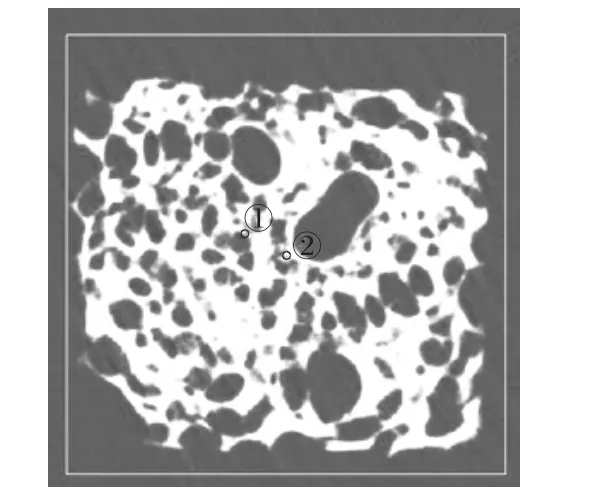
圖5 未知介質的幾何形狀及位置信息

基于所構建模型，將原模塊中的橢圓替換成與小圓圓心對稱的半徑為其二倍的大圓，兩圓心關于正方形幾何中心對稱。探測器單元間距方法與原標參模型相同，但是由于兩個模塊相互影響較小，可以選取的數據點變多，擬合精度會提高，所得間距更接近真實值。

4 模型評價

本文的幾何標參模型運用了CT投影定理，基于擬合的正弦圖像，較好地求解了旋轉中心的位置，準確地標定了相關參數。在傅里葉逆變換基礎上建立起的反變換模型，是通過先卷積后反變換的方式進行的，引入濾波有效地降低了模塊間斷點的震蕩效應，提高了反變換所得吸收率的精度。其缺點為：由于數據擬合的原因，誤差大小在一定程度上受數據點數量影響。

[1]陳建林，閆鑌，李磊，等.CT重建中投影矩陣模型研究綜述[J].CT理論與應用研究，2014，23（2）：317-328.

[2]王浩.CT不完全投影數據重建算法研究[D].大連：大連理工大學，2008.

[3]王文發，劉彥保.傅里葉變換用于圖像處理時的特性分析[J].延安大學學報（自然科學版），2006（3）：22-24.

[4]盧彥斌.X射線CT成像技術與多模態層析成像技術研究[D].北京：北京大學，2012.

[5]Baek J，Pelc N J.Gain correction for a CT system：US7734004[P].2010.