影響風電機組主軸溫度的因素分析及其預警應用

文 | 邱國祥，唐徐立，王明軍，高原生

隨著風電機組運行時間增加，各部件出現不同程度的磨損，無論電氣設備或者機械設備損壞都將帶來直接經濟損失，尤其大部件出現問題，將帶來巨大損失。所以，對機組運行狀態進行監控以及預防檢修應該引起足夠重視。

軸承溫度升高會使潤滑油質量下降，使主軸熱脹、材料變形、降低軸承壽命，嚴重時會導致軸承失效、停止工作。通過研究主軸軸承的溫度監測數據和其潛在故障之間的關系，進而基于主軸軸承的溫度監測數據對主軸軸承進行狀態預測，來提高主軸工作的可靠性。

本文分析了正常運行風電機組主軸實際溫度的影響因素及特征，通過數據處理得到未運行狀態的主軸溫度（定義為零狀態溫度），再使用線性回歸方法建立主軸實際溫度與零狀態溫度的關系，得到機組主軸溫度的特性參數，進而推算出主軸預測溫度。基于預測溫度提出了新的報警值設定方法，當實際主軸溫度與設置的偏離容許值出現偏差，則觸發報警，然后通過對主軸發生故障機組的歷史數據進行分析，驗證了此方法的可行性。最后對現有的簡單保護參數提出修改優化建議。

影響因素分析

主軸實際溫度主要受到潤滑狀況、環境溫度、機組功率、風速、空氣密度、主軸轉速、傳動鏈轉矩等因素的影響。針對潤滑狀況良好的機組，主軸實際溫度可以使用這些變量的函數形式來表示：

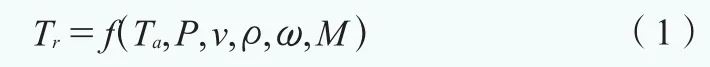
其中：

Tr——主軸實際溫度

Ta——環境溫度

P ——機組功率

v ——風速

ρ ——空氣密度

ω ——主軸轉速

M ——傳動鏈轉矩

而機組功率與風速、空氣密度、主軸轉速、傳動鏈轉矩存在的關系如式（2）所示：

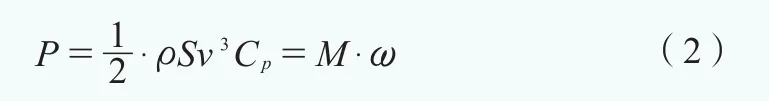
其中：

S ——風輪掃風面積

Cp——風輪利用系數

所以，針對潤滑狀況良好的機組，通過研究環境溫度、機組功率對機組主軸實際溫度的影響，即可找出主軸溫度的變化規律，從而對主軸溫度進行預測，如式（3）：

通過選取某1.5MW風電機組正常運行（潤滑良好）一年的數據，利用比恩法原理，構造微小間隔的環境溫度區間，分析功率對主軸溫度的影響。

具體方法如下：按照間隔為5℃進行環境溫度區間劃分（也可以選取更小區間）。例如：在5～10℃，10～15℃區間，主軸實際溫度隨機組功率變化的散點分布，以及全溫度段每5℃間隔的線性回歸關系如圖1－圖3所示。

可以看出，在機組環境溫度穩定的情況下，主軸實際溫度幾乎不受機組功率的影響，隨著環境溫度的升高而升高，但整體高出10～20℃左右。

因此，本文將重點分析正常機組主軸實際溫度隨環境溫度變化的規律，利用歷史數據推算主軸溫度，當實際運行機組軸承溫度與推算的主軸溫度偏離超過容許值時發出報警，從而幫助運維人員在主軸損壞前檢查機組主軸潤滑狀況，避免造成更大的損失。

利用歷史數據推算主軸溫度

一、零狀態溫度的確定

從上述分析可以看出，主軸實際溫度隨環境溫度變化而變化，并且整體高出10～20℃左右。假定機組長期未運行，則可以斷定主軸實際溫度將和環境溫度非常接近。因此，機組靜止狀態與運行狀態存在差別。為此，需要先確定機組長期未運行時的規律。

從選取的機組數據中篩選出功率P＝0kW，轉速ω＝0rpm時的狀態，如圖4所示：

可以發現，機組停機后，約120個點（一個點10min，總計20h）后，主軸實際溫度隨環境溫度的波動而波動，整體滯后約36個點（一個點10min，總計6h）。

在機組長時間停機后，觀察主軸實際溫度與環境溫度的關系可以發現，主軸實際溫度隨著環境溫度周期波動，但因機艙的保溫作用，主軸實際溫度隨著環境溫度變化有一定的滯后。因此，將機艙作為一個一階保溫系統，以環境溫度為基礎，采用公式（4）推算出機組處于停機狀態下的主軸溫度，即零狀態溫度T0。

其積分公式如式（4）所示：

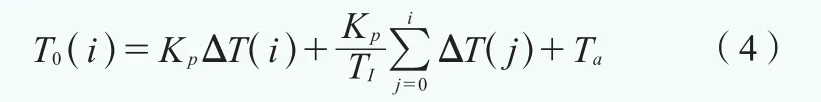
其中：

T0——零狀態溫度Ta——環境溫度Kp——比例系數TI——積分系數

T(i) ——i時刻主軸實際溫度與環境溫度的差值通過歷史記錄的環境溫度數據，應用公式（4）可得到零狀態溫度。圖5描述了零狀態溫度隨環境溫度變化的趨勢，可以看出停機狀態下零狀態溫度與主軸實際溫度較吻合，這說明上述零狀態溫度的模型準確。

二、建立主軸實際溫度與零狀態溫度的關系

機組在靜止狀態下，主軸實際溫度隨環境溫度規律波動；當機組從停機到短暫運行，溫度會急劇上升。所以為了找到運行狀態下的主軸溫度規律，需要對原始數據進行篩除。

（1）停機數據剔除：每次停機時間長短不一，因此，需要將停機數據全部剔除；

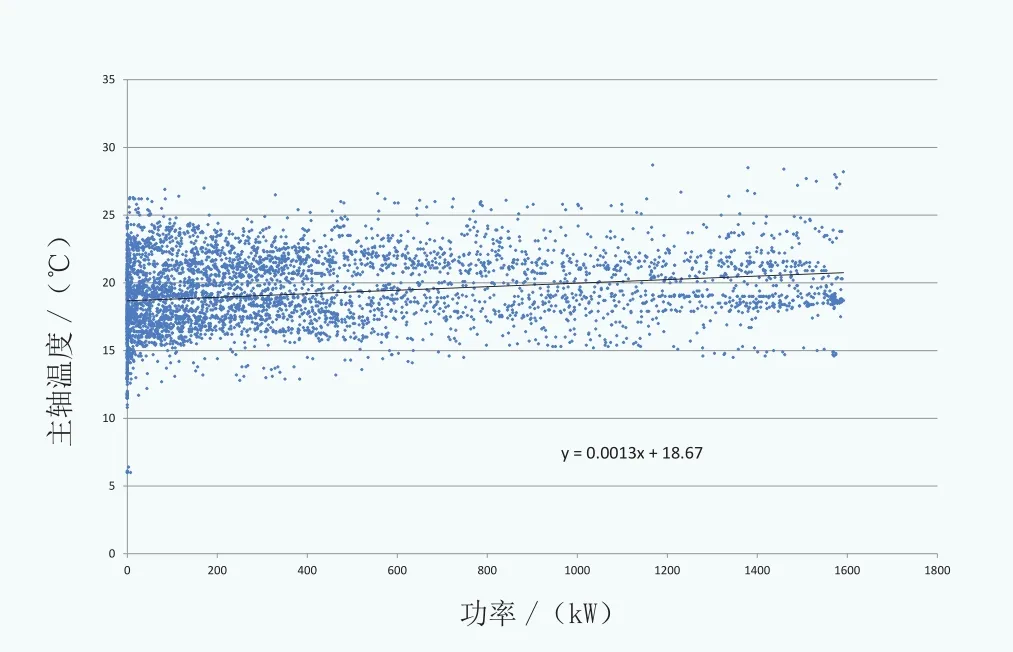
圖1 5～10℃區間，主軸實際溫度隨機組功率變化的關系

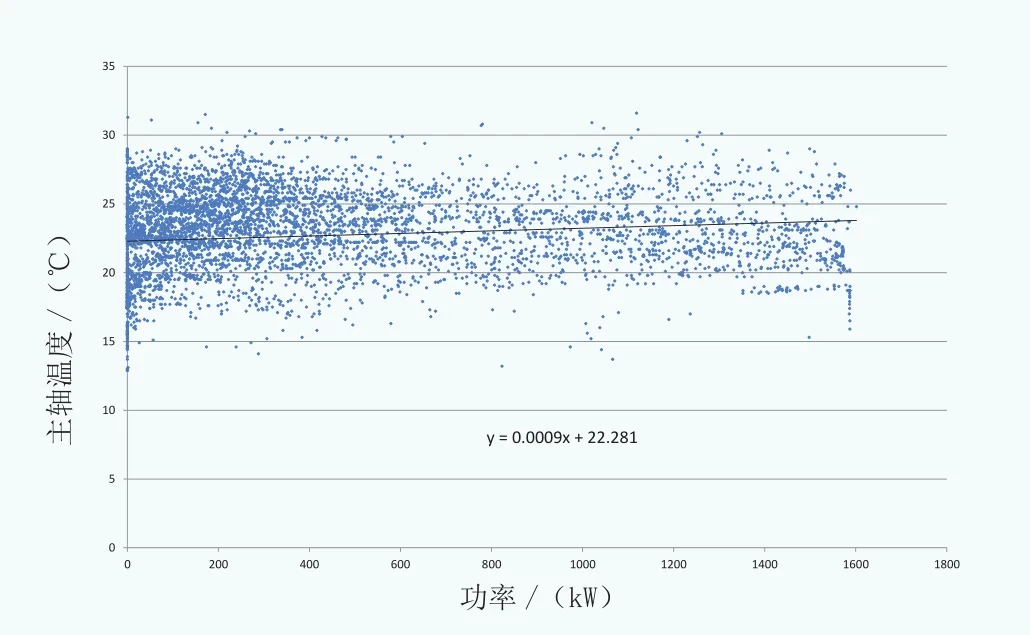
圖2 10～15℃區間，主軸實際溫度隨機組功率變化的關系

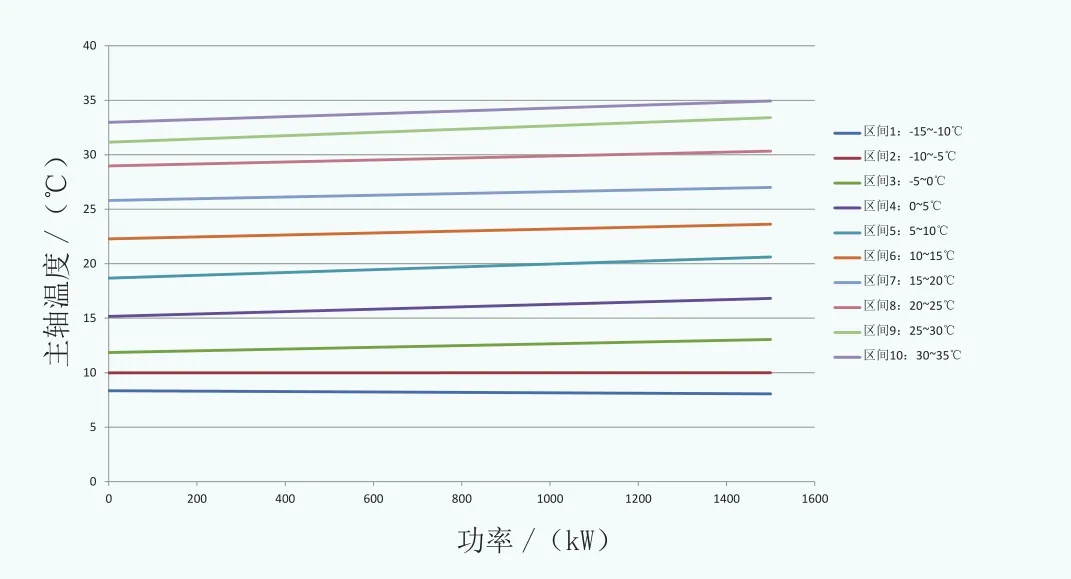
圖3 各溫度區間主軸實際溫度與機組功率的線性回歸關系

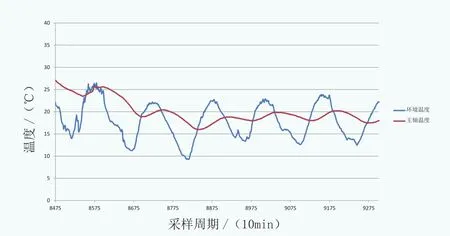
圖4 主軸實際溫度與環境溫度隨時間變化的關系

（2）并網數據剔除：由于機組啟動前，停機時間不同，主軸溫度與環境溫度，并不一定達到熱交換平衡；當機組從停機到短暫運行，溫度會急劇上升。因此，需要剔除機組剛運行時的數據（此文剔除了并網2h內的數據）。

綜上，本文在建立溫度關系時，剔除了停機時的數據，以及機組并網不足2h的數據。

風電機組SCADA系統中存儲了大量歷史數據，包括歷史主軸實際溫度和環境溫度，首先以歷史環境溫度數據組為基礎求出T0數據組（見公式4），再根據歷史主軸實際溫度數據組和T0數據組，運用線性回歸方法，求解出該風電機組的比例特性參數K和偏移特性參數b（見公式5）。線性回歸圖如圖6所示。

線性回歸表達式如式（5）所示：

其中：

Tr——主軸實際溫度

T0——零狀態溫度

K ——比例特性參數

b ——偏移特性參數

三、運用K、b特性參數得到主軸預測溫度

在運用歷史數據得到該風電機組的比例特性參數K和偏移特性參數b后，即可對風電機組后續運行過程中的主軸溫度進行預測，如公式（6）：

其中：

Tx——主軸預測溫度

T0——零狀態溫度

K ——比例特性參數

b ——偏移特性參數

主軸預測溫度的應用

風電機組的溫度保護，一般都是設置一個溫度上限，作為報警、故障閾值。

但實際上，設備的溫度與環境溫度變化存在波動關系，因此，當設備出現溫度偏高（例如，此時環境溫度很低）時，并不一定能夠觸發此設定的閾值，無法起到準確保護作用，直到運行到更加惡劣的狀態后才出現報警。

本文提出一種新的報警值設定方法，根據風電機組以往的運行數據，合理確定溫度偏離容許值 B0。隨后利用公式（6）得到的主軸預測溫度，用公式（7）求得溫度偏離值B，當B大于B0時，則發出報警，用此方法可以提前發現主軸問題。

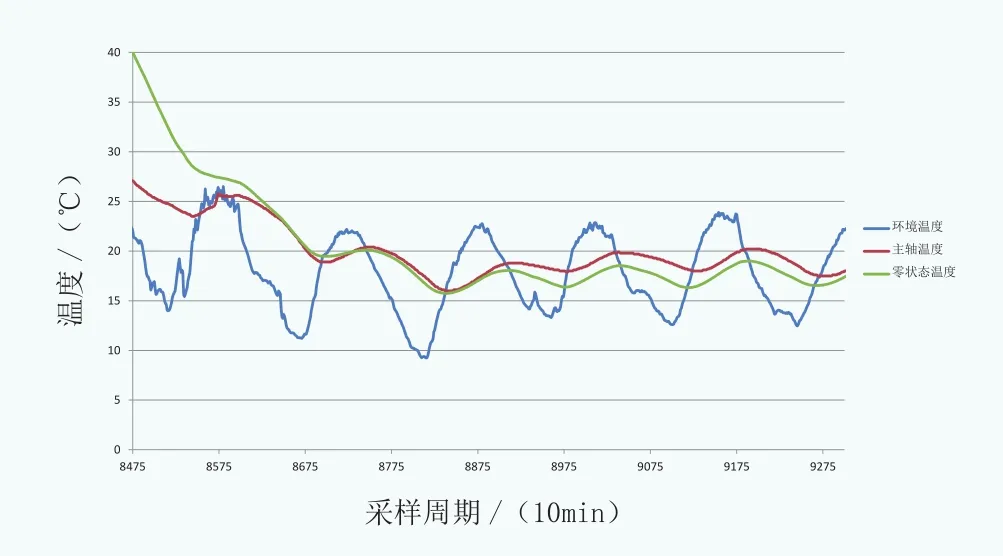
圖5 零狀態溫度與實際主軸溫度隨時間變化的關系

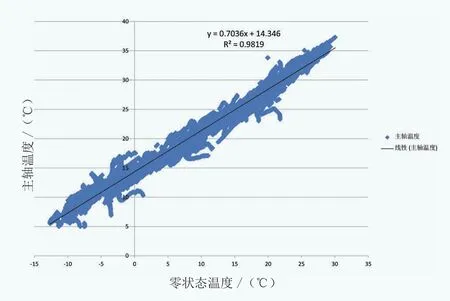
圖6 零狀態溫度—主軸實際溫度線性回歸圖

其中：

B ——溫度偏差值

Tx——主軸預測溫度

Tr——主軸實際溫度

選取內蒙古某FD87-2MW風電場某臺機組作為驗證機組。此機組前期運行正常，后期運行過程中出現了主軸溫度高的報警。因此，選取本臺機組，不但可以驗證正常情況下此方法是否合理，也可以驗證預警方法是否可用。

首先選取正常情況下的歷史數據，運用線性回歸法建立主軸溫度與零狀態溫度的關系，得到該臺風電機組的比例特性參數K＝0.7198、偏移特性參數b＝11.016，則該機組的主軸預測溫度如公式（8）所示：

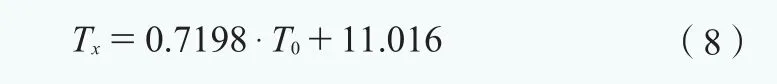
定義偏離容許值 B0＝6，當偏離值大于6℃時，發出故障信號。主軸溫度、實際偏離值隨時間的變化如圖7所示。

本臺機組報出“主軸溫度高”時間為T2（2016年10月15日），若使用此方案，則可以在T1（2106年10月5日）發現異常，提前發現故障，可以提前檢查。

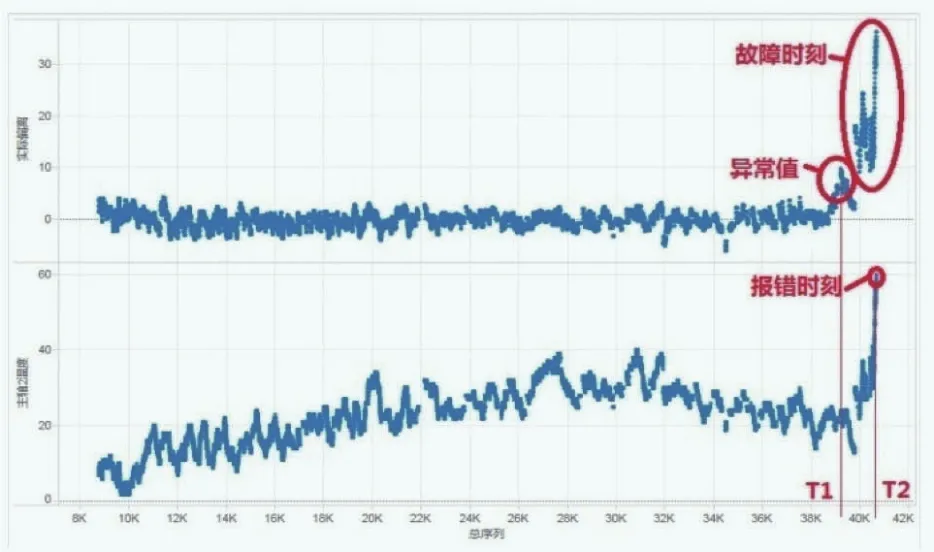
圖7 主軸溫度、偏離值隨時間的變化

結語

本文通過分析發現，環境溫度是影響主軸溫度的最主要因素。通過數據處理，得到零狀態下的主軸溫度，再使用線性回歸方法，建立主軸溫度與零狀態溫度的關系。

同時提出了新的報警值設定方法，當主軸預測溫度與主軸實際溫度的偏差超過溫度偏離容許值時，則觸發報警。通過在故障機組上進行驗證發現，這種方法不但有效，還可以提前發現問題。若及時對故障進行處理，則可以避免大部件出現更嚴重的損壞。

為了使此方法更可靠準確，后期可以通過對每種機型在不同運行工況下進行分析，總結大數據，對此方法進行進一步修正，應用于主軸溫度實時監控預警。后續可以將此方法進行推廣，應用于風電機組齒輪箱、發電機等部件的溫度保護閾值參數設定及故障預警等工作中。

攝影：王志遠