承臺對群樁-承臺結(jié)構(gòu)水動力特性的影響研究
唐自航, 祝 兵
(西南交通大學(xué)橋梁工程系,四川成都 610031)
根據(jù)波浪傳播方向與群樁中心連線的方向的夾角,通常把群樁的布置分成縱向串列、橫向并列和傾斜布置三種基本形式,群樁的布置形式會顯著影響樁所受到的波浪荷載。國內(nèi)的學(xué)者開展了許多實驗來研究群樁效應(yīng),主要研究在雙樁串列、并列和三樁串列、并列等幾種情況下,群樁效應(yīng)系數(shù)KG隨群樁數(shù)量、群樁布置形式、相對樁距和KC數(shù)等影響因素的變化規(guī)律[1-5]。群樁效應(yīng)系數(shù)KG是以單根樁的受力為基準(zhǔn),群樁結(jié)構(gòu)中各組成樁所受的力與單樁所受的力的比值。
但以上的研究都只針對于群樁結(jié)構(gòu),而沒有考慮承臺對群樁效應(yīng)的影響,但在實際的跨海橋梁中,下部結(jié)構(gòu)總是以群樁-承臺結(jié)構(gòu)這一形式存在。由于承臺尺寸相比于樁徑大很多,會對作用在樁上的波浪力的大小產(chǎn)生顯著影響,因此群樁-承臺結(jié)構(gòu)實際的群樁效應(yīng),與以上研究得出的結(jié)論相比,會有較大差別。此外,國內(nèi)外學(xué)者在研究近海工程的問題時,大都采用物理模擬來研究和解決問題。但實驗水槽等的建立占用場地面積較大,相關(guān)的配套設(shè)施設(shè)備的價格高昂,導(dǎo)致科研成本很高。不僅如此,實驗水槽的結(jié)果的準(zhǔn)確性也受制于物理尺度、實驗設(shè)備和測量儀器等因素。
本文在對群樁水動力特性現(xiàn)有研究的基礎(chǔ)上,建立了群樁結(jié)構(gòu)的三維數(shù)值模型,運(yùn)用FLOW-3D進(jìn)行數(shù)值模擬計算,得到了群樁效應(yīng)系數(shù)KG隨KC數(shù)的變化曲線,結(jié)果與相同條件下實驗室的實測數(shù)據(jù)高度吻合,充分證明本文采用的數(shù)值模擬方法是準(zhǔn)確可靠的。在此基礎(chǔ)上,建立了群樁-承臺結(jié)構(gòu)的三維數(shù)值波浪水槽,并通過改變承臺淹沒系數(shù)以研究其對群樁-承臺結(jié)構(gòu)的水動力特性的影響。
1 數(shù)值波浪水槽模型
1.1 控制方程
在使用FLOW-3D軟件進(jìn)行數(shù)值模擬時,將波浪視作不可壓縮的黏性牛頓流體。控制方程由連續(xù)性方程和動量方程構(gòu)成, FLOW-3D軟件采用了FAVOR技術(shù),因此分別在連續(xù)性方程式(1)和動量方程式(2)~式(4)中加入體積參數(shù)和面積參數(shù),控制方程如下:
(1)
(2)
(3)
(4)
式中:u、v、w分別為x、y、z方向上的速度分量;Ax、Ay、Az分別為x、y、z方向上的流動面積分?jǐn)?shù);Gx、Gy、Gz分別表示在x、y、z方向上的重力加速度分量;P表示波壓力;ρ表示流體密度;VF表示體積分?jǐn)?shù);fx、fy、fz分別為x、y、z方向上粘性力引起的加速度分量。
1.2 湍流模型
本文采用k-ε湍流模型實現(xiàn)對上述方程的封閉,以保證波浪結(jié)構(gòu)相互作用的計算的準(zhǔn)確性。在方程中加入體積參數(shù)和面積參數(shù),具體如下:
(5)
(6)
式中:kT表示湍動動能;εT表示湍動耗散率;PT則表示速度梯度引起的湍流動能產(chǎn)生項;C1、C2、C3為常數(shù),其值分別取為1.44、1.92和0.2;DkT與Dε表示擴(kuò)散項。
1.3 自由液面追蹤與邊界條件
在建立數(shù)值水槽時,采用VOF法來進(jìn)行自由液面追蹤。
邊界條件的設(shè)置是建立數(shù)值水槽的關(guān)鍵之一,本次數(shù)值水槽采用的邊界條件如下:
(1)入流邊界:采用速度入口法造波。
(2)出流邊界:采用Sommerfeld輻射邊界條件消波。
(3)對稱邊界:在數(shù)值水槽的左右兩側(cè)和水槽的頂面采用對稱邊界。
(4)壁面邊界:水槽的底面邊界采用粗糙壁面邊界,且為非滑移邊界。
(5)自由液面:水槽的動力學(xué)邊界條件取P等于大氣壓強(qiáng)P0,自由液面切應(yīng)力取為0。
2 數(shù)值波浪水槽的驗證
基于Bonakdar[6]于2014年對群樁結(jié)構(gòu)的群樁效應(yīng)進(jìn)行的水槽實驗,使用FLOW-3D建立結(jié)構(gòu)物的數(shù)值水槽,將計算結(jié)果與實驗數(shù)據(jù)進(jìn)行對比,從而驗證結(jié)構(gòu)物數(shù)值模擬的可行性及準(zhǔn)確性。實驗水槽的具體設(shè)置和波浪參數(shù)參見文獻(xiàn)[6]。
2.1 群樁布置形式
群樁布置形式如圖1所示。
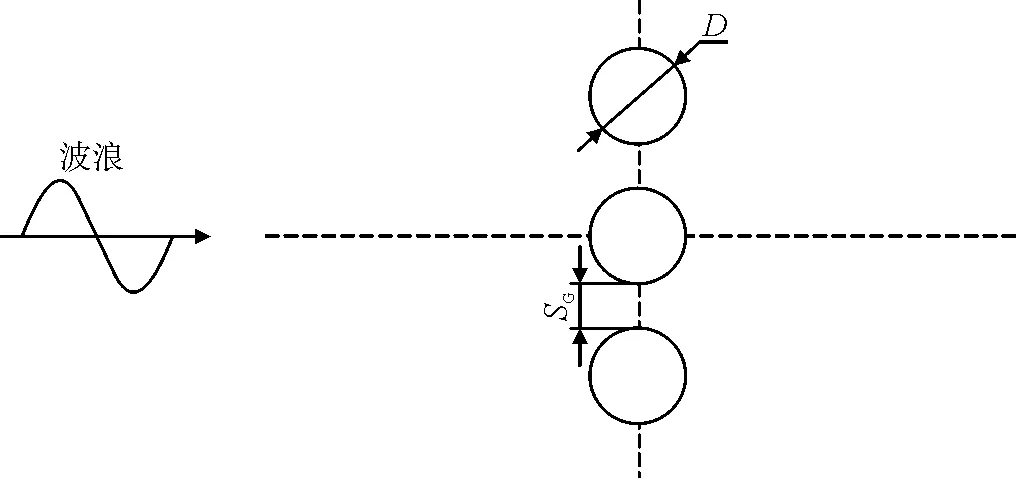
(a) 橫向并列

(b) 縱向串列圖1 群樁布置形式
2.2 相對樁距
相對樁距SG/D定義為相鄰兩根樁的外表面距離SG和樁的直徑D之比。在此次驗證過程中,僅選擇相對樁距為1的情況進(jìn)行分析。
2.3 數(shù)值水槽設(shè)置
數(shù)值水槽的長、寬、高尺寸分別為5 m、1.5 m、1 m。群樁結(jié)構(gòu)的中心點位于距離入流邊界1 m處,同時也處于水槽長度方向的中心軸上。
2.4 數(shù)值模擬結(jié)果與實驗結(jié)果對比
通過數(shù)值模擬得到群樁中組成樁的最大波浪力,再與單樁的最大波浪力相除可以得到隨KC數(shù)變化的群樁效應(yīng)系數(shù)KG曲線,并與實驗結(jié)果比較(圖2)。
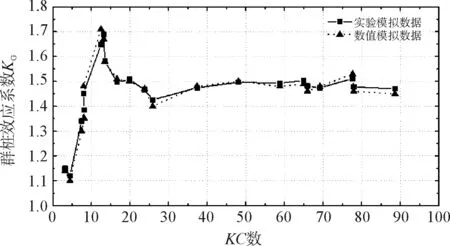
(a)群樁結(jié)構(gòu)橫向并列布置
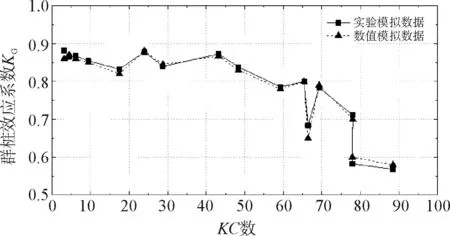
(b)群樁結(jié)構(gòu)縱向串列布置圖2 數(shù)值模擬與實驗群樁效應(yīng)系數(shù)KG對比
由圖2可知:在群樁結(jié)構(gòu)的布置形式分別為橫向并列、縱向串列兩種情況下,數(shù)值模擬的結(jié)果與實驗結(jié)果吻合性良好,充分證明數(shù)值模擬方法研究結(jié)構(gòu)物所受的波浪力作用是可行的。
3 計算結(jié)果與討論
為了研究承臺淹沒系數(shù)對群樁-承臺結(jié)構(gòu)水動力特性的影響,在相同的波浪參數(shù)和不同承臺淹沒系數(shù)下進(jìn)行數(shù)值模擬。共選取12組波浪進(jìn)行模擬,具體波浪參數(shù)如表1所示。
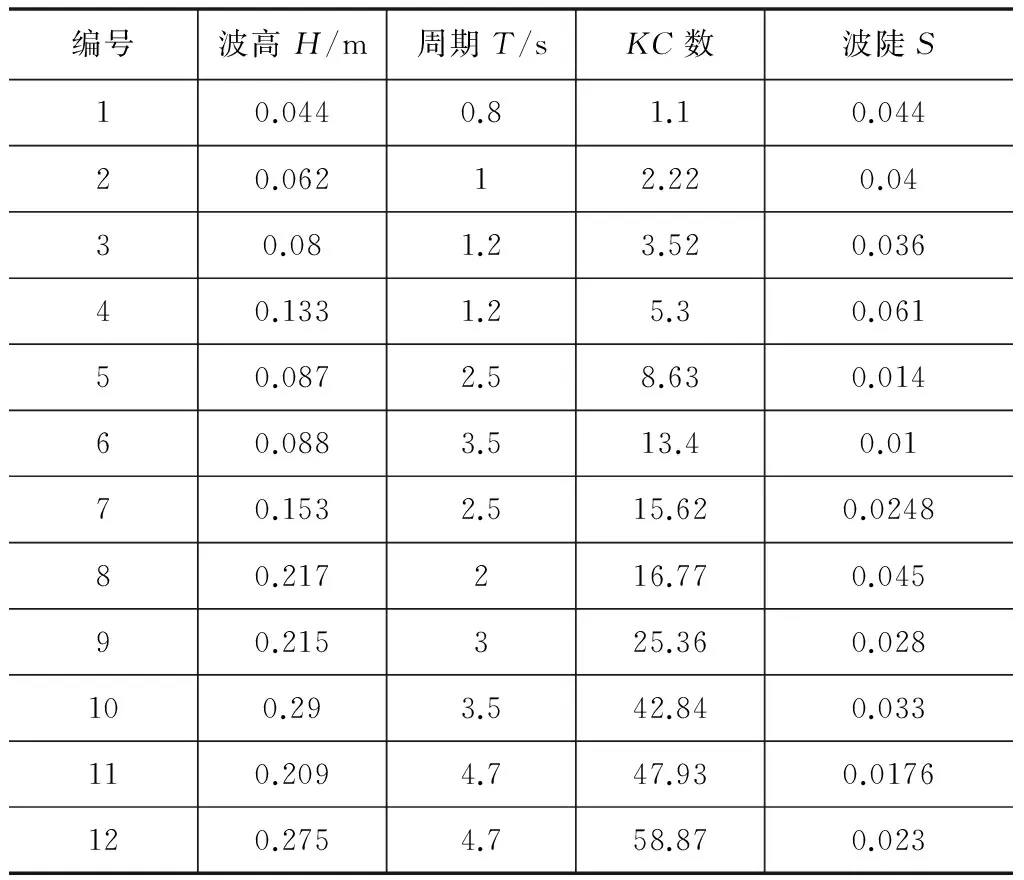
表1 波浪參數(shù)
波浪參數(shù)輸入時,波浪加載時長統(tǒng)一取為波浪周期的10倍,以保證數(shù)值模擬計算結(jié)果的準(zhǔn)確性。
當(dāng)下部群樁的布置為橫向并列,且相對樁距分別為0.5、0.75和1以及承臺淹沒系數(shù)分別為0、1和2時的群樁效應(yīng)系數(shù)KG曲線如圖3所示。
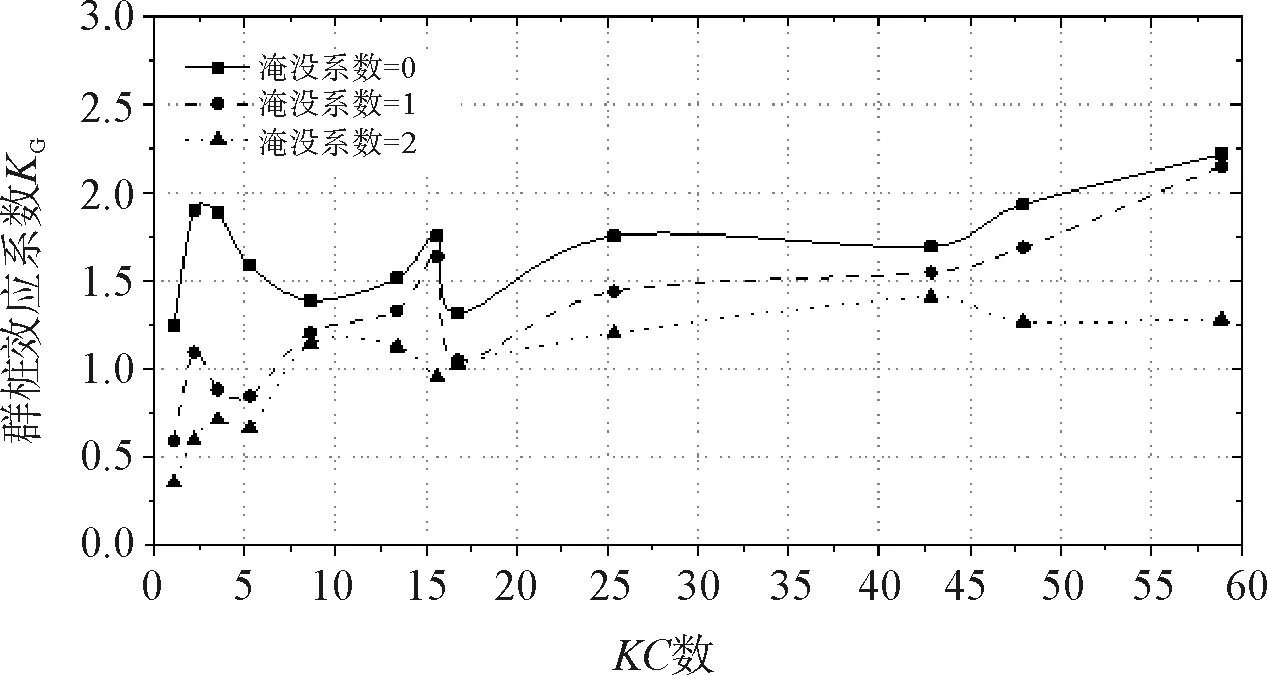
(a)相對樁距=0.5
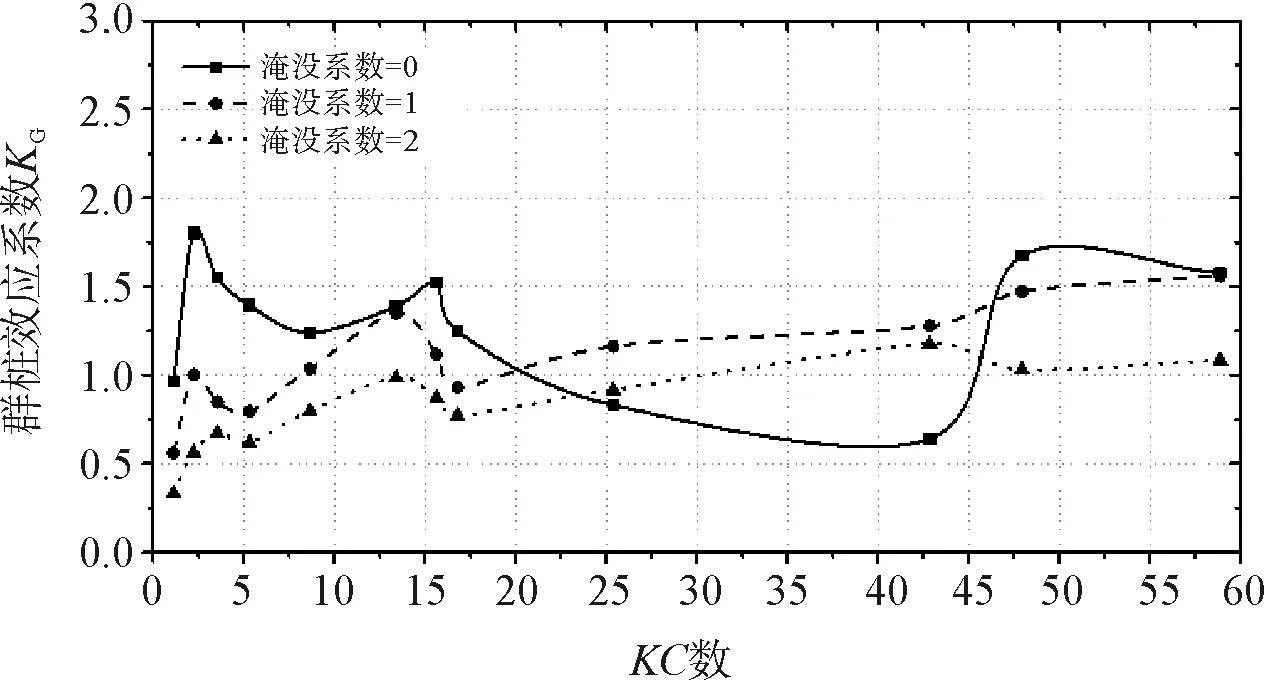
(b)相對樁距=0.75
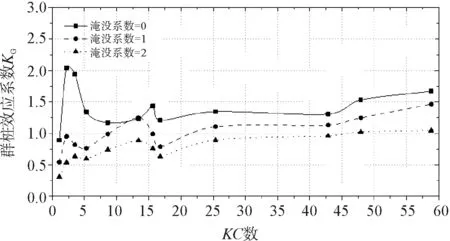
(c) 相對樁距=1圖3 橫向并列時不同承臺淹沒系數(shù)下群樁效應(yīng)系數(shù)KG曲線
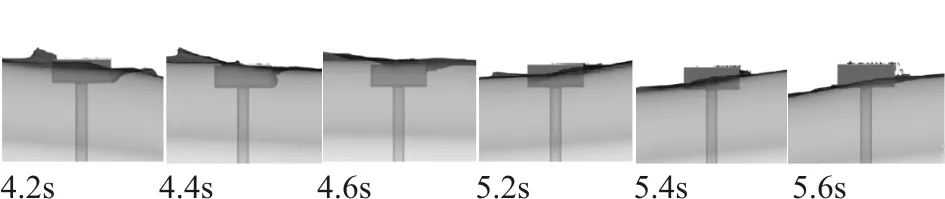
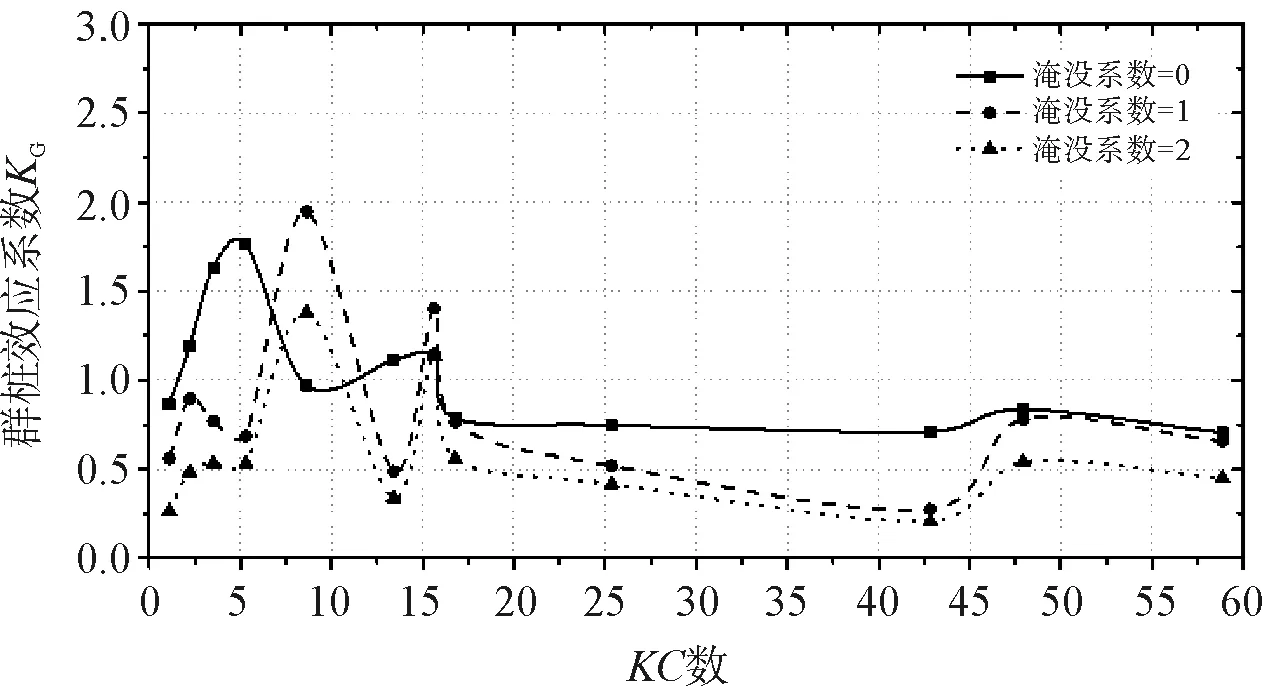
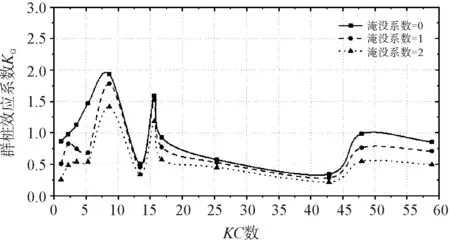
由圖3可知:(1)當(dāng)相對樁距為0.5或1,承臺淹沒系數(shù)的增大使得群樁效應(yīng)系數(shù)KG減小。(2)當(dāng)相對樁距為0.75,0 當(dāng)下部群樁的布置為縱向串列時,且相對樁距分別為0.5、0.75和1以及承臺淹沒系數(shù)分別為0、1和2時的群樁效應(yīng)系數(shù)KG曲線如圖4所示。 (a) 相對樁距=0.5 (b)相對樁距=0.75 (c) 相對樁距=1圖4 縱向串列時不同承臺淹沒系數(shù)下群樁效應(yīng)系數(shù)KG曲線 由圖4可知:(1)相對樁距為0.5及1時,在數(shù)值模擬所取KC數(shù)范圍內(nèi),即0 為了簡單分析承臺淹沒系數(shù)的改變對水動力特性的影響,圖5給出了群樁結(jié)構(gòu)為橫向并列時,某一波峰經(jīng)過時間內(nèi)組成樁周邊的波壓力圖及波面圖。 圖5表示下部群樁布置為橫向并列、相對樁距為1,且KC數(shù)為42.84,承臺淹沒系數(shù)Cs為別為0和1時,群樁-承臺結(jié)構(gòu)的組成樁在一個波峰時間內(nèi)(t=4.2~5.6 s)的波壓力和波面圖,其中波浪的傳播方向為從左到右。由圖5可知:承臺淹沒系數(shù)的改變會對群樁所受到的波浪力產(chǎn)生很大的影響。對比圖5(b)、圖5(c)可以發(fā)現(xiàn),在其他條件相同時,由于靜水面的提高,會使得群樁結(jié)構(gòu)周圍波壓力在整體上都有所增大,從而影響了各組成樁所受波浪力的大小,而這一影響會反映在群樁效應(yīng)系數(shù)的改變上。 本文采用數(shù)值模擬的方法研究承臺淹沒系數(shù)對群樁-承臺結(jié)構(gòu)水動力特性的影響,主要考察群樁效應(yīng)系數(shù)KG隨承臺淹沒系數(shù)的變化規(guī)律。 (1)本文所建立的群樁結(jié)構(gòu)的三維數(shù)值模型的計算結(jié)果與之前實驗室的實驗數(shù)據(jù)高度吻合,充分證明計算模型是準(zhǔn)確可靠的,因而可以采用數(shù)值模擬的方式來研究群樁-承臺結(jié)構(gòu)的水動力特性。 (a)圖例 (b)CS=0時波壓力圖 (c)CS=1時波壓力圖 (d)CS=0時波面圖 (e)CS=1時波面圖圖5 CS=0及CS=1時波壓力圖、波面圖 (2)承臺淹沒系數(shù)的改變會對群樁效應(yīng)系數(shù)KG產(chǎn)生影響,且群樁分別在并列和串列兩種不同布置時,承臺淹沒系數(shù) 的改變對群樁效應(yīng)系數(shù)KG所產(chǎn)生的影響略有不同。 (3)承臺的存在對群樁效應(yīng)系數(shù)KG有很大的影響,在研究樁群效應(yīng)對海上橋梁群樁-承臺結(jié)構(gòu)中各組成樁的波浪力的影響時,建議考慮承臺對群樁效應(yīng)的影響。 [1] 俞聿修,張寧川. 雙樁樁列上的不規(guī)則波浪力[J]. 大連理工大學(xué)學(xué)報,1988(1):103-112. [2] 俞聿修,張寧川. 三樁樁列上的不規(guī)則波浪力[J]. 中國港灣建設(shè),1989(3):1-7. [3] 張寧川,俞聿修. 隨機(jī)波浪作用于三樁樁列上的橫向力的水動力特征及群樁效應(yīng)[C]// 全國海岸工程學(xué)術(shù)討論會, 1993. [4] 李玉成,王鳳龍. 作用于串列雙樁樁列上的波流力[J]. 水動力學(xué)研究與進(jìn)展,1992(2):141-149. [5] 李玉成,王鳳龍,王洪榮. 作用于并列雙樁樁列上的波流力[J]. 海洋學(xué)報,1992,14(2):106-121. [6] Bonakdar L, Oumeraci H. Pile group effect on the wave loading of a slender pile: A small-scale model study[J]. Ocean Engineering, 2015, 108: 449-461. [7] Bonakdar L, Pile group effect on the wave loading of a slender pile[D]. TU Braunschweig, Germany 978-3-86948-383-2, 2014. [8] 高學(xué)平,曾廣冬,張亞. 不規(guī)則波浪數(shù)值水槽的造波和阻尼消波[J]. 海洋學(xué)報,2002,24(2):127-132.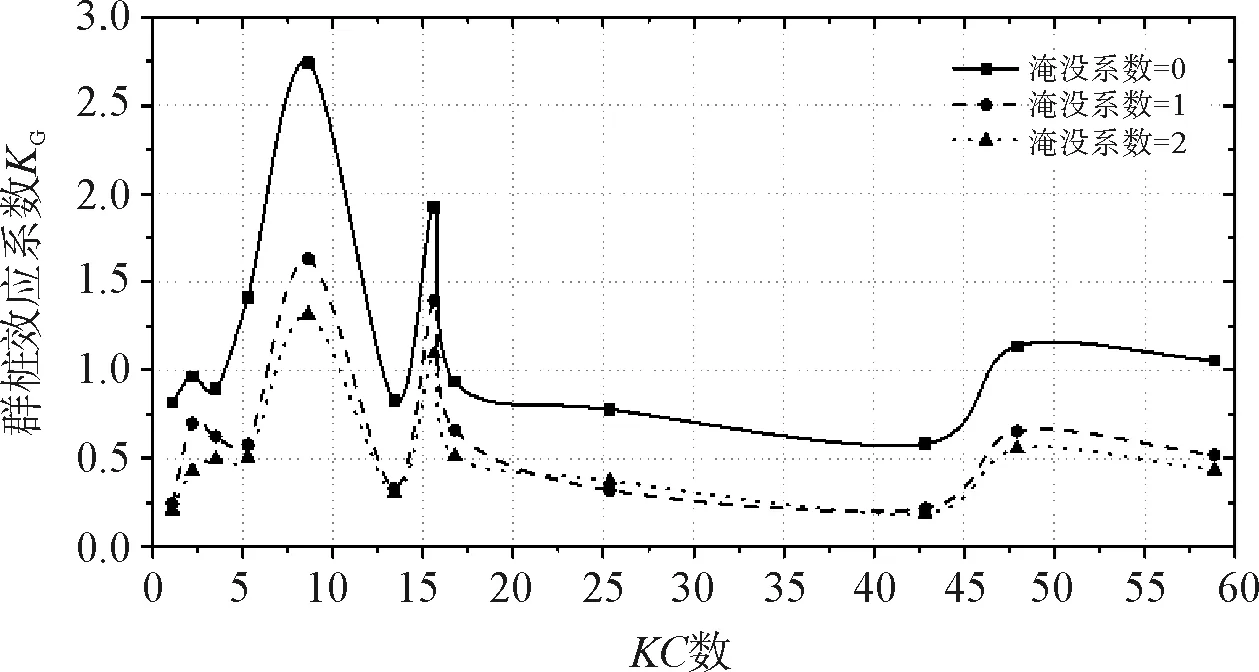
4 結(jié)論