龍河大橋地震響應時程分析
高金亮, 楊 俊
(四川省交通運輸廳公路規劃勘察設計研究院, 四川成都 610041)
1 工程概況
麗江至攀枝花高速公路龍河大橋半幅寬12.5 m,上部結構采用18×30 m簡支T梁,下部結構采用雙柱式墩,由于橋位處地形變化較大,本文選擇橋墩高度最高的一聯第8-11
孔做抗震分析,第7-11號橋墩高度依次為:45.5 m、47.5 m、40 m、34 m、30 m,由于7號墩頂為滑板支座,其地震作用較小,本文選取最不利的8號橋墩進行地震響應時程分析,橋梁立面圖見圖1所示。
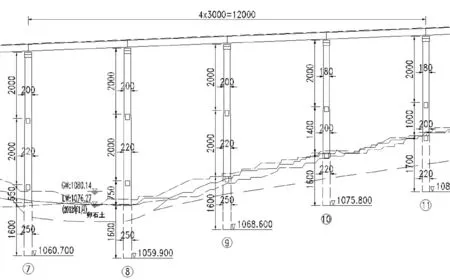
圖1 橋梁立面
2 地震參數取值
本橋地震動峰值加速度為0.1g,反應譜特征周期為0.45 s,場地類型為II類,屬于高速公路上的橋梁,為B類橋梁。根據《公路橋梁抗震設計細則》,橋梁抗震設防措施等級為8級。
3 計算模型及計算方法
采用Midas Civil有限元軟件建立全橋三維空間桿系模型,進行地震響應時程分析。中墩采用板式支座,聯端采用四氟滑板支座,所以模型中沒有建立聯端橋墩;支座縱、橫向的剪切剛度均采用彈性連接進行模擬;橋墩樁基采用“m”法(土彈簧)模擬,在軟件中通過節點彈性支撐來實現。
4 地震響應時程分析法
本橋8號橋墩最大墩高47.5 m,已大于《公路橋梁抗震設計細則》規定的30 m,屬于非規則橋梁,需采用時程分析法進行抗震分析。通過時程分析法可以計算出地震過程中每一瞬時結構的位移、速度和加速度反應,較為準確的計算出結構在地震過程中的內力和位移隨時間的反應,并發現結構在地震過程中可能存在的薄弱環節或可能發生的震害,是計算地震反應較為真實的精細分析方法。
依據本橋所在的場地類型,根據GB 50011-2001《建筑抗震設計規范》的規定,選取兩組實際強震記錄和一組人工模擬的加速度時程曲線,將三組數值取平均后與振型分解反應譜法所采用的地震影響系數曲線做比較,得出與本橋適用的地震波。幅值的調整:
(1)設計加速度峰值PGA的求法:
PGA=Smax/2.25=CiCsCdA
(2)E1地震時程縫隙所用地震加速度時程曲線的最大值:
PGA1 =CiCsCdA=0.5×1.3×1.0×0.1×9.8
=0.637 m/s2
(3)E2地震時程縫隙所用地震加速度時程曲線的最大值:
PGA2 =CiCsCdA=1.7×1.3×1.0×0.1×9.8
=2.1658 m/s2
調整后的地震波如圖2所示。
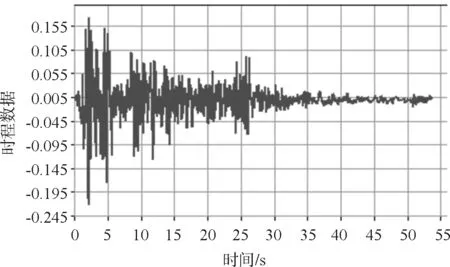
圖2 調整后的地震波
(4)地震波特征周期Tg的確定。
因為擬相對速度反應譜PSV和擬絕對加速度的反應譜PSA之間有近似關系PSA=W·PSV,則可以得到特征周期:
Tg=2π(1/w)=2π(EPV/EPA)
其中:EPA為有效峰值加速度;EPV為有效峰值速度。
可求得EPA及EPV的對數坐標如圖3、圖4所示。
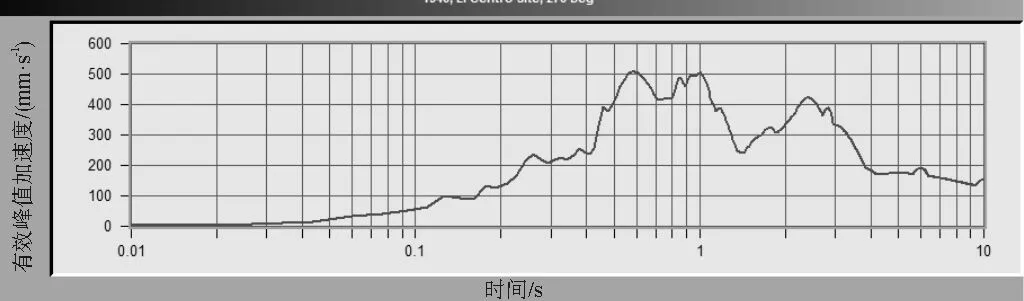
圖3 EPA的對數坐標
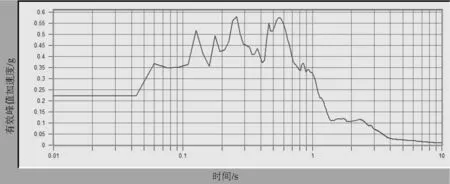
圖4 EPV的對數坐標
EPV=0.38 m/s;EPA=4.8 m/s2
Tg=2π(EPV/EPA)=2π(0.38/4.8)=0.49742 s
該橋所在場地地震特征周期為0.45 s,與實錄特征周期0.497 42較為接近,故實錄波的特征周期適用于本橋。
5 時程分析法計算結果
采用集中鉸彈塑性梁單元對橋梁延性構件橋墩進行模擬,在E2地震作用下對橋墩進行Pushover分析,可以得到墩底截面的彎矩-轉角關系曲線,以及橋墩的最大彎矩、軸力、墩頂最大位移等。
墩底彎矩(圖5)在2.24 s達到最大值16 600 kN·m,在12.31 s達到最小值-10 250 kN·m。
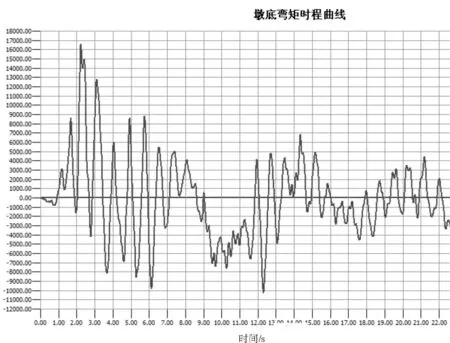
圖5 墩底彎矩時程曲線
在地震作用激勵下,墩頂位移(圖6)在2.46 s時達到最大,最大值約22.7 cm。
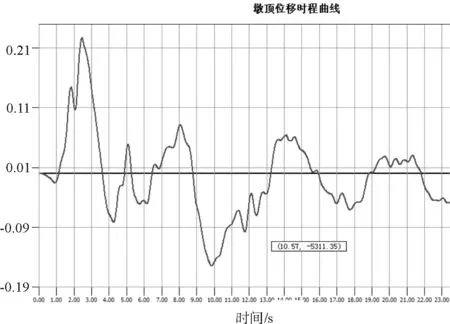
圖6 橋墩墩頂位移時程曲線
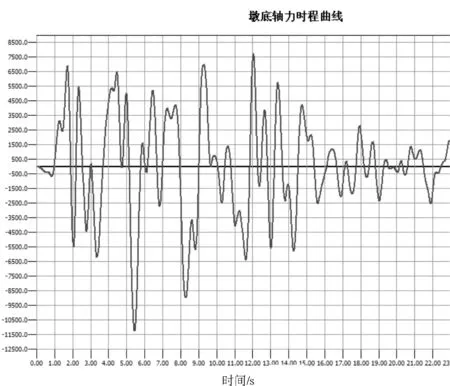
圖7 橋墩墩底軸力時程曲線
橋墩墩底轉動角(圖8)在2.24 s時達到最大轉角0.001 213 rad。
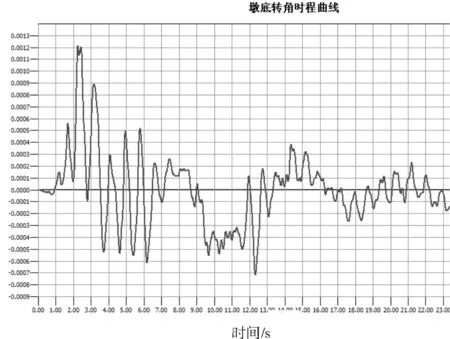
圖8 橋墩墩底轉角時程曲線
通過圖5~圖8可以清晰的看到在地震過程中橋墩的彎矩、軸力、轉角、墩頂位移隨著時間變化,并發現在2.24 s附近橋墩的受力最不利。
塑性鉸區域的塑性轉角計算過程如下:
Lp1=2/3×b=2/3×250=166.7 cm
Lp2=0.08H+0.22fyds=466.4cm>0.044×400×2.8=49.28 cm
Lp取166.7 cm
圓形截面的等效屈服曲率Φy:
ΦyD=2.213×0.002
Φy=2.213×0.002/2.2=0.00177(1/m)
圓截面的極限曲率Φu:
(1)ΦuD=(2.826x10-3+6.850εcu)-(8.575x10-3+18.638εcu)(P/fc/Ag) =0.0328
(2)ΦuD=(1.635x10-3+1.179εs)-(28.739xεs2+0.656εs +0.010)(P/fc/Ag)=0.08
取兩者中的較小值:
Φu=0.0328/2.5=0.013135
塑性鉸區域的最大容許轉角θu
=Lp(Φu -Φy)/K
=166.7/100x(0.0328-0.00177)/2=0.00947
根據共軛梁法可求得整個橋墩構件潛在塑性鉸區域的塑性轉角θp
θp=0.003874+0.000282+0.000022=0.0042
θp <θu,滿足規范要求。
Δ容=1/3x27.52×0.00177+(27.5-166.7/2)x0.00947=0.797m
Δ=22.7cm<Δ容=79.7cm
通過計算可以得出順橋向的最大曲率小于墩底截面的屈服曲率,即地震作用下墩底截面并未進入屈服狀態;橋墩墩頂位移小于容許位移值;從墩底截面的彎矩-轉角滯回曲線(圖9)可以看出橋墩在地震作用下墩底截面有開裂現象發生。
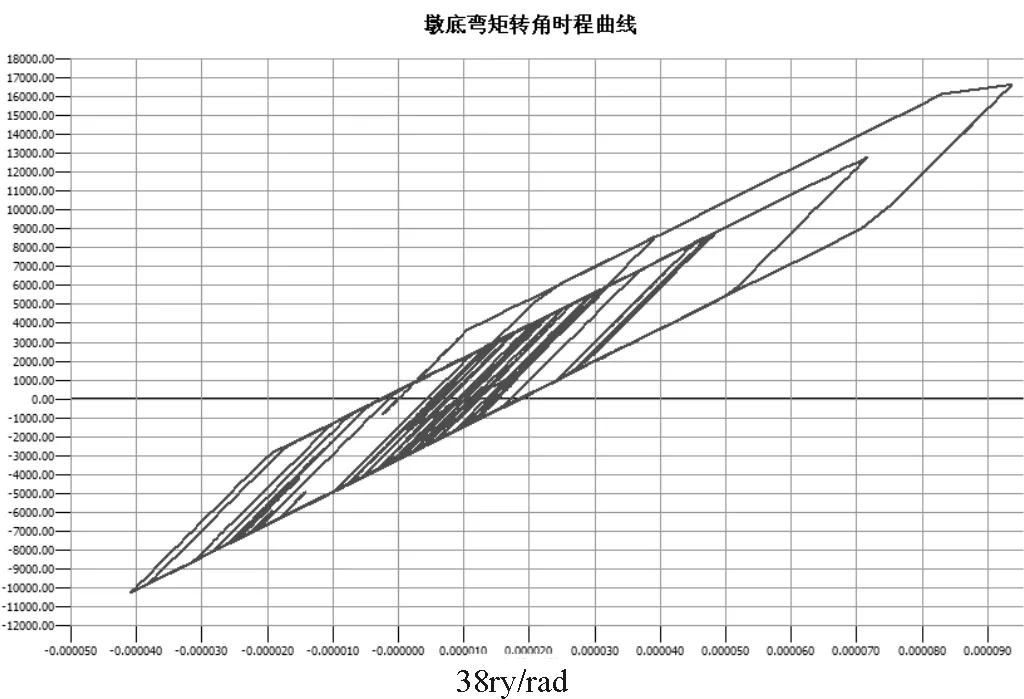
圖9 墩底截面的彎矩-轉角關系曲線
6 結束語
本文對高墩橋梁下部結構采用時程分析法進行地震分析,橋墩墩頂位移、墩底截面轉角等均小于規范的容許值;本文時程分析法選取地震波的過程及通過Pushover進行塑性分析,對非規則橋梁的抗震分析具有指導意義,可供廣大橋梁工程設計者借鑒。
[1] JTG/T B02-01-2008《公路橋梁抗震細則》[S].
[2] JTG D62-2004《公路鋼筋混凝土及預應力混凝土橋涵設計規范》[S] .
[3] 范立礎. 橋梁抗震[M].上海:同濟大學出版社,1997.
[4] 范立礎,卓衛東. 橋梁延性抗震設計[M]北京:人民交通出版社,2001.

