部分斜拉橋溫度場和溫度效應分析

刁 飛， 唐自航， 黃 彪

(西南交通大學土木工程學院，四川成都 610031)

統計大量實際工程發現，溫度作用所產生的混凝土箱梁的應力和變形直接影響橋梁結構的安全性、適應性和耐久性。因此，如何準確模擬溫度場分布以及研究溫度作用下的結構響應是橋梁設計、施工和養護維修的難點和重點。

本文針對處于有劇烈溫差變化的某城際鐵路矮塔斜拉橋，利用Ansys有限元計算軟件，根據天文學基本理論，運用python進行編程模擬該橋梁的日照溫度場初始邊界條件，對模型進行熱分析，分析該橋溫度場、應力、應變分布規律。

1 工程背景

1.1 橋梁概況

本文所選取的模型為某城際鐵路矮塔斜拉橋，橋跨布置為(97+176+97)m(圖1)。

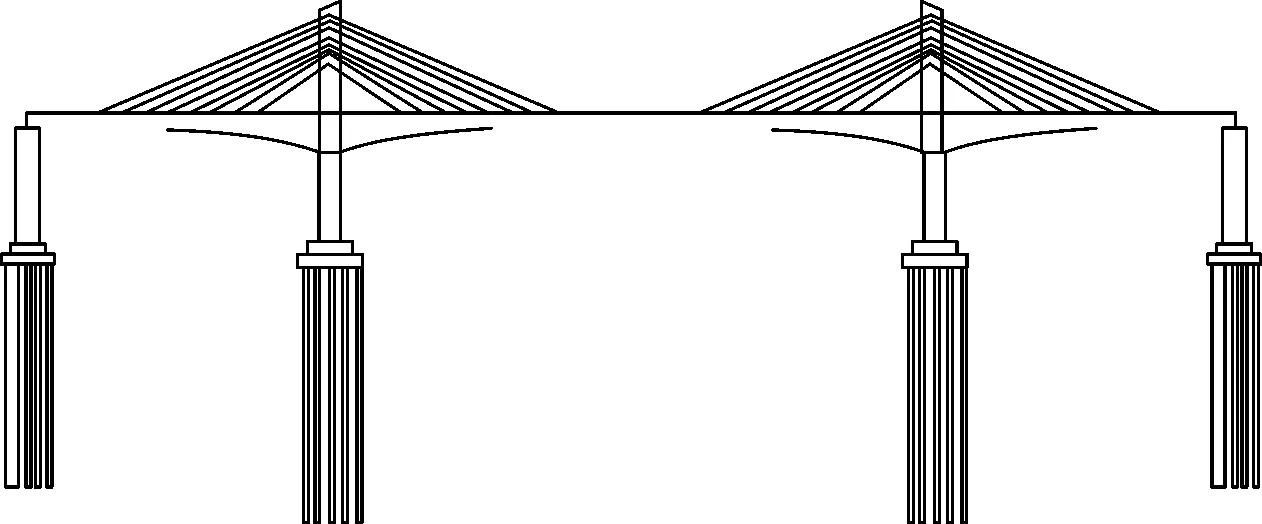
圖1 全橋平面示意

該橋主梁采用單箱雙室直腹板箱型截面，截面高度采用梁底線型為二次拋物線y=0.0005602x2的高度形式。箱梁邊跨梁端和中跨跨中截面梁高均為5.6 m，支座處梁高9.3 m，橋面寬度13.5 m，箱寬11 m(圖2)。

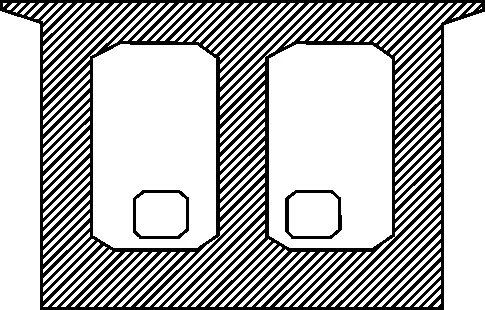
(a)墩頂截面

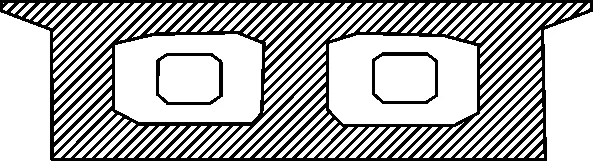
(b)梁端截面

1.2 橋梁有限元模型

通過有限元軟件ANYSY建立了箱梁截面的有限元模型，在進行溫度場分析時，用PLANE55單元模擬梁截面。PLANE42平面應變單元可以模擬橫向纖維與橫向框架的約束，用于求解溫度自應力與溫度次應力。對于縱向次內力的求解采用MIDAS/CIVIL建立梁單元全橋模型，設置對應邊界條件，并施加溫度梯度荷載。材料參數如表1 。圖3為ANSYS二維截面模型，圖4為Midas空間有限元模型。

表1 材料參數

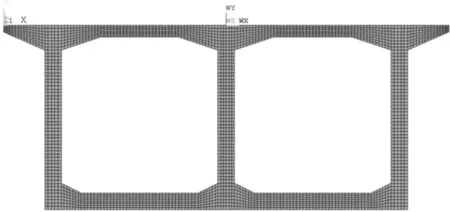
圖3 箱梁截面模型

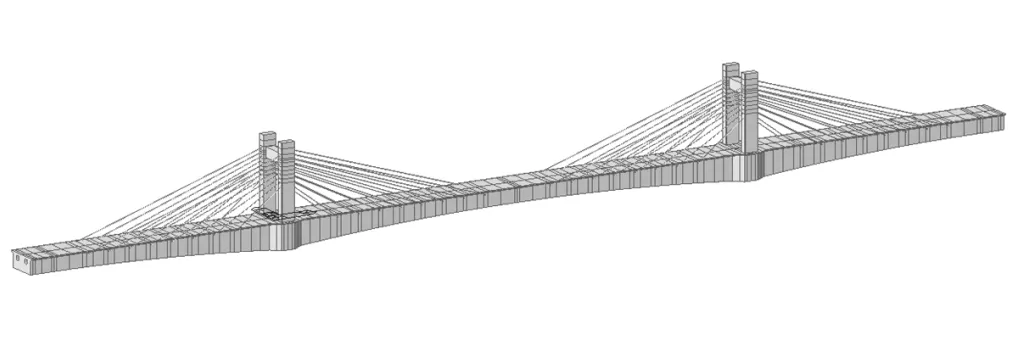
圖4 橋梁有限元模型

2 溫度場有限元分析

橋梁溫度場是與時間、空間相關的四維函數。橋梁結構縱向長度遠遠大于橫向尺寸，并且橋梁跨度內其縱向地理經緯度、風速、氣溫與太陽輻射強度等變化均非常小，可近似認為沒有變化。因此，假定箱梁溫度場沿其縱向沒有變化，可以把箱梁溫度場簡化為二維非穩態溫度場問題。

2.1 溫度場基本理論

本文溫度場分析時主要考慮了第二類和第三類邊界條件。綜合考慮箱梁溫度場邊界條件的影響因素短波輻射、長波輻射和對流換熱。

2.1.1 箱梁溫度場邊界條件

(1)

ANSYS熱分析過程中，不能直接將不同類型邊界條件直接疊加計算，需要轉換成同一種邊界條件，如式(2)中，存在已知熱流密度的第二類邊界條件和已知熱交換系數的第三類邊界條件，本文采用將第二類邊界條件以第三類邊界條件形式表示：

(2)

2.1.2 箱梁內部邊界條件

箱梁內部邊界只存在內壁混凝土與箱內空氣的熱交換，通常箱梁內部日溫度變化較小，且由于處于封閉空間基本無空氣流動。因此熱交換系數hc按v=0 m/s計算。其邊界條件可以表示為：

(3)

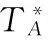
由此可以看出，箱梁溫度場邊界條件求解的實質就是建立空氣介質綜合溫度數組。

“每一只生肖瑞獸都有獨特的個性氣質。描繪它們時，我試圖擺脫其外在形象的束縛，用心感受亞洲文化，從而在狹小的表盤中展現這些氣質。”Anita Porchet表示。“豐富的黑白色調能夠創造出細膩的灰色動物毛皮質感，并形成風格低調的背景，凸顯狗的昂揚神采。”

2.2 主梁溫度場初始溫度

本文通過考慮短波輻射、長波輻射、對流換熱、陰影長度、日出日落時刻與環境氣溫等因素，采用編程軟件，完成了對頂板、底板、翼緣板底部、不同陰影長度腹板以及箱梁內壁的溫度邊界條件的建立。對于每個分組得到48個溫度點，模擬一天的邊界條件，給定10 d為周期，通過重復施加邊界條件求解，判斷是否收斂。結果如圖5，箱梁溫度到第4 d以后已經收斂。

圖5 箱梁溫度時程曲線

2.3 溫度場計算結果分析

為了進一步的體現截面溫度場分布情況，選取梁段截面具有代表意義的點做如圖6所示的編號。得到關鍵點24 h內的溫度變化時程曲線，分析得出最不利溫差時刻，并提取了截面沿梁高與板厚方向的溫差分布曲線。

圖6 關鍵點與關鍵截面編號

在一天內，由于太陽輻射的影響，箱梁會經歷升溫到降溫的過程，白天由于有太陽輻射且混凝土導熱性能較差，箱梁表面和內部形成正溫差。晚上則相反形成負溫差。箱梁內外表面溫度的交替升高降低，使得各板均存在兩個近似等溫時刻，由于輻射的情況不同，各個板出現等溫時刻有所差異。

頂板和底板的溫度時程曲線如圖7、圖8。頂板的外部溫度波動大于內部，外表面溫度變化范圍接近24 ℃，內部變化范圍不到5 ℃。白天由于頂板不斷吸收太陽輻射和環境溫度升高，14∶00出現最大正溫差，該時刻截面溫度分布如圖9(c)。夜間由于環境溫度降低，箱梁向外部輻射熱量，且混凝土導熱性能差，到5∶30出現最大負溫差，該時刻截面溫度分布如圖9(a)。由于太陽輻射的影響和氣溫逐漸升高，頂板外部氣溫迅速升高，在8∶00左右溫度達到內外溫度平衡狀態。底板關鍵點溫度時程曲線趨勢和頂板大致相同，但是由于接受到的太陽輻射小于頂板，內外溫度平衡狀態的出現時間為9∶00左右，晚于頂板。

由于東腹板在日出時接受太陽直射，外表面迅速升溫，不到4 h就達到了一天之內最高溫度，并且相比于其它板件最先達到了等溫時刻(7∶00)。對于西腹板而言，其整個上午均處于陰影之中輻射強度較小，因此升溫緩慢，在10∶30達到內外溫度相等，所有板件中最晚，此時截面溫度分布如圖9(b)。在17∶00時，西腹板出現最高溫度，為最晚出現最高溫度的板件，對應截面溫度分布如圖9(d)。中腹板關鍵點的溫度變化不大，這是因為中腹板受到的太陽輻射影響最小。

2.4 最不利溫差

箱梁截面進行溫度應力分析時，需要確定溫度分布最不利時刻。由溫度時程曲線可以看出不同部位最不利溫差出現的時候。當箱梁外表面溫度高于內部溫度時，稱為正溫差；反之成為負溫差。本文主要針對正溫差，提取最大梁高溫差與鐵路規范進行對比(圖10)。

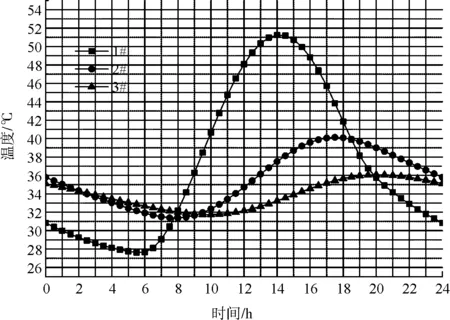
圖7 頂板溫度時程曲線

圖8 底板溫度時程曲線

(a)5∶30

(b)10∶30

(c)14∶00

(d)17∶00

(a)A-A截面

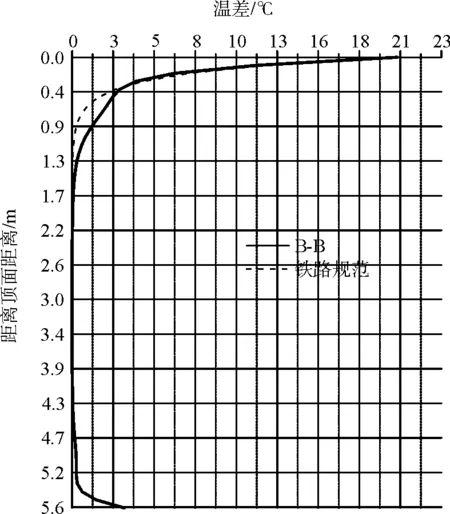
(b)B-B截面

(c)C-C截面

在頂板范圍內，截面溫差和基本符合規范要求，在腹板范圍內，對于東腹板，由于受到太陽輻射的影響，溫差略大于鐵路規范，在靠近底板處取得最大值1 ℃。鐵路規范沒有對底板溫差做規定，但是可以看出底板也存在3～4 ℃的溫差。

腹板最大正溫差與按規范計算相差較大，分析原因可能是：規范標準截面在計算沿板厚方向溫差時，并未考慮截面方位角、截面傾角與翼緣板對腹板溫度分布影響。并且不同箱梁的形狀，材料有所差異。

3 結構溫度效應分析

混凝土箱梁截面上存在的溫度應力按作用方向可以分為橫向溫度應力與縱向溫度應力。縱向溫度應力又可以按照產生原因分為縱向溫度自應力與縱向溫度次應力；同理橫向溫度應力也可以分成橫向溫度次應力與橫向溫度自應力。橫向溫度次應力是由于截面橫向框架約束引起，縱向溫度次應力則是由于橋梁本身存在的多余約束引起。

計算求得箱梁截面各個時刻溫度場分布之后，將熱分析單元轉換成結構分析單元以完成橫向溫度應力與縱向溫度自應力的求解(圖11)。

(a) σx

(b) σy

(c) σz圖11 沿梁高度方向最大正溫差應力分布

由于頂板和腹板接受太陽輻射值較大，因此高應力區主要集中在頂板和腹板位置。箱梁截面水平溫度應力主要集中在頂板位置，豎向溫度應力主要集中在外腹板，其他位置所受應力較小。在沿梁高度方向最大正溫差作用下，在13∶30到17∶00左右，橋梁橫向的最大水平拉應力達到了3.61 MPa，最大豎向拉應力達到1.2 MPa。在沿梁高度方向最大正溫差作用下，縱向溫度自應力最大值為4.67 MPa，其最大拉應力位置出現在翼緣板拐點上，分析原因是由于拐點處于雙向傳熱狀態，加之尺寸較小，因此溫度變化幅度較大，使其縱向溫度自應力明顯高于箱梁截面其它位置。這也與翼緣板拐點經常出現混凝土脫落這一普遍現象相吻合(圖12)。

(a)受壓側

(b)受拉側圖12 沿梁高度方向最大溫度縱向次內力分布

根據溫度場模擬得到，沿高度方向的等效線性溫差在14∶00時達到最大。因此，圖12給出在14∶00時主梁的縱向溫度次應力圖。

在橋梁自身多余約束的影響下，沿梁高最大溫差會引起橋梁較大的溫度次內力。高度方向溫差最大縱向約束拉應力為4.91 MPa，壓應力為4.73 MPa。橋梁在沿梁高溫差作用下的效應不可忽視，設計時應該充分考慮橋梁的截面溫度場變化。

4 結束語

(1)混凝土箱梁溫度場受到橋址處太陽輻射強度、氣溫、風速、材料和截面構造形式等因素的影響，計算箱梁溫度場時應該綜合考慮。

(2)混凝土箱梁溫度場分布不均勻并且隨空間和時間周期性變化，對橋梁結構的影響較大，設計時應充分考慮溫度作用的影響。

(3)箱梁橫向溫度應力主要集中在頂板和外腹板位置，縱向溫度自應力在翼緣板拐點處出現最大值，分析原因是由于拐點處于雙向傳熱狀態，加之尺寸較小，因此溫度變化幅度較大，使其縱向溫度自應力明顯高于箱梁截面其它位置。

(4)橋梁自身的多余約束對縱向溫度次內力影響較大，設計時應綜合考慮橋梁邊界條件和溫度場特點，避免較大溫度次內力產生。

[1] 魏光坪.單室預應力混凝土箱梁溫度場及溫度應力研究[J].西南交通大學學報, 1989(4):90-97.

[2] 李全林.日照下混凝土箱梁溫度場和溫度應力研究[D].長沙：湖南大學，2004.

[3] 許國良. 工程傳熱學[M].北京:中國電力出版社, 2005.

[4] Kehlbeck F著. 太陽輻射對橋梁結構的影響[M].劉興法譯.北京:中國鐵道出版社，1981.

[5] 劉興法. 預應力混凝土箱梁溫度應力計算方法[J]. 土木工程學報, 1986(1):46-56.

[6] 康為江. 鋼筋混凝土箱梁日照溫度效應研究[D]. 湖南大學, 2000.

[7] 屈兆均. 用有限單元法解溫度應力的計算原理[J]. 橋梁建設, 1982(3):27-52.

[8] Jain P C. A model for diffuse and global irradiation on horizontal surfaces[J]. Solar Energy, 1990, 45(5):301-308.

[9] 劉興法. 混凝土結構的溫度應力分析[M]. 北京; 人民交通出版社, 1991.

[10] 李健,趙坪銳,萬章博,等.雙塊式無砟軌道溫度場試驗研究和數值分析[J].中國科學: 技術科學,2014,44( 7):729-735.

[11] 趙坪銳,李健.無砟軌道溫度場報告[R].成都:西南交通大學,2014: 1-44.

[12] 劉興法.預應力混凝土箱梁溫度應力計算方法[J].土木工程學報, 1986, 19(1): 44-54.

[13] 中華人民共和國行業標準.TB 10002.1-2005.鐵路橋涵設計基本規范[S].北京：中國鐵道出版社，2005.

[14] 管敏鑫.混凝土箱形梁溫度場、溫度應力和溫度位移的計算方法[J]. 橋梁建設, 1985(1):40-49.

[15] 葉見曙, 賈琳, 錢培舒. 混凝土箱梁溫度分布觀測與研究[J]. 東南大學學報(自然科學版), 2002, 32(5):788-793.

[16] Hunt B, Cooke N. Thermal calculation for bridge design. Journal of the Structural Division[J]. ASCE.1975. 101(9):1763-1781.

[17] 中國氣象科學數據共享服務網.http://cdc.cma.gov.cn/index.jsp.

[18] Cope R J. Concrete Bridge Engineering: Performance and advances[J]. European Journal of Operational Research, 1987, 138(3):554-568.