走出思維誤區,培養學生思維能力
施響勇
(江蘇省啟東中學 226200)
一、走出“定性思維”誤區,激發學生探究興趣
許多高中生本來就對數學學習心生“畏”懼,再加上高中數學理論的枯燥乏味,導致很多學生對學科學習缺乏興趣.然而,數學教學是一種雙邊活動,其特殊性要求教學需要高度的師生配合,反之則效果不佳,難以達到預期目標.因此,有效激發學生數學學習興趣,充分調動其學習積極性,就成為高中數學教學亟待解決的問題.這就需要我們教師去認真思考、精心準備.在數學教學活動中,我們教師可以通過讓學生使用數學方法進行思考、分析和解決現實生活中的實例,以此讓學生感受到生活中處處包含數學,生活離不開數學,進而引導學生重視數學學科的學習.比如在學習概率內容時,針對社會上不法分子的擺地攤賭博行為,我舉了如下例子:
路旁推主甲用一個口袋裝了8個白球和8個黑球,摸獎者每人交一元的參與費,然后從袋中一次性去摸出5個球,如果摸到5個白球可獎勵20元現金;如果摸到4個白球可獎勵2元現金;如果摸到3個白球可獎勵紀念品一份(價值5毛錢);其他情況無任何獎品.問按摸1000次統計,攤主是賺錢還是賠錢?
很多人認為有利可圖,就紛紛上鉤,失敗了也只是認為運氣不好而已,卻不知這里包含了數學中的概率問題.學生們對該例子也很有興趣,他們也有人認為攤主可能面臨很大的風險,于是我和學生們一起討論了這個問題.
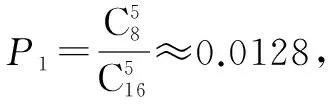
二、走出重“果”輕“因”誤區,培養學生邏輯能力
公式推導是高中數學課堂教學的重要內容,涉及概念、方法以及技巧,對于學生思維、能力的培養有重要作用.然而,在實際教學中,師生都忽略了這一點,常常重“果”輕“因”,不注重公式的推導過程,止步于公式記憶,這是高中數學教學與學習普遍存在的誤區.對此,就要加強重視,積極改善,一方面,注重公式的推導過程,并在公式推導過程中有意識地摻雜一些邏輯推理技巧展示給學生;另一方面,加強意識滲透,引導學生走出學習過程中重“果”輕“因”的誤區.
在講解等比數列求和公式的推導過程時,我就引導學生發現并利用等比數列的特點,巧妙地在等式兩端同時乘以公比q而后作差,從而得到等比數列求和公式.這一方法也是學生解決數列求和問題中最常用的方法.
在本題的求解過程中應用的正是該方法.因此我們在教學過程中要求學生記住的并不僅僅是等比數列前n項和的公式,理解并熟知推導過程與公式變形也是要求掌握的內容.另外,在數學公式的推導教學過程中,對在解題時經常用到的步驟要著重講解,引導學生逐步走出重“果”輕“因”的誤區,促進其邏輯推理和解決問題的能力的培養.
三、走出“數形分家”誤區,培養解題技巧能力
數形結合一直以來都是解決高中數學問題的有效方法之一,但很多高中生一般對“數字”比較敏感,往往會對“形”有些陌生,不善于或想不到利用數形結合的思想方法去分析解決數學問題,缺乏這方面的解題技巧.
例若關于x的方程x2+2kx+3k=0的兩根都在-1和3之間,求k的取值范圍
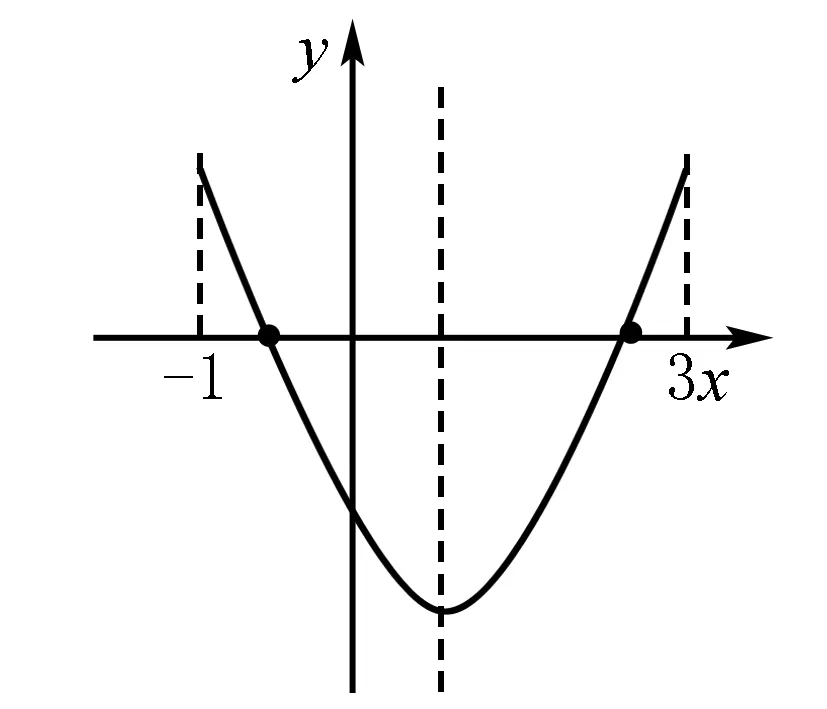
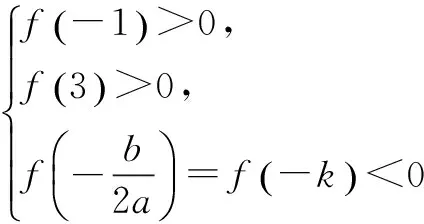
利用數形結合的方法可以很快解決該問題,可是在實際解題過程中我發現很多學生無從下手,我經過提問得知,很多學生認為這明明是“數”的問題,根本就沒有利用“形”來解決問題的意識,因而無法解決此問題.像這樣腦海中完全沒有“形”的概念,無法靈活利用圖象來分析解決問題,就是大部分高中生的通病.針對這一問題,在實際教學過程中特別是學習幾何、函數內容時,要求學生熟練掌握各種函數圖象,使其腦海中有由“數”想到“形”、由“形”聯系到“數”的概念,并利用數形結合的思想來分析解決數學問題,最終達到培養他們解題技巧能力的目的,為以后更好的發展打下基礎.
總之,激發學生學習興趣,引導學生走出數學學習的誤區,是高中數學教學長期關注的問題.在這之后,才能更好的培養學生學習數學的興趣,掌握正確的數學學習方法,教學質量才會有提高的可能.
參考文獻:
[1]向乾華.淺談中小學數學思維訓練與培養[J].讀與寫(教育教學刊),2017(05).
[2]鄭步春.數學思維訓練型課堂的建構與實踐[J].江蘇教育研究,2016(27).

