體驗中感悟讓數學思想扎根
——由一道期末試題引發對《數與形》的再思考
張麗萍
【教學過程】
一、自主探究,發現規律
1.出示雜亂的16個(4種不同顏色)小正方形。先讓學生觀察,并提出活動要求:(1)你能不能將這些小正方形重新分一分、擺一擺,讓我們更加容易地看出小正方形的總個數?(2)想一想:根據你們的擺法可以寫出哪個算式?
2.學生自主探究、擺拼。
(教師巡視、采樣)
預設:

圖1

圖2(雜亂)

圖3(規律)
反饋:
(1)看到圖1你想到了哪個算式?你是怎么想的?
(2)同時出示圖2和圖3,它們有什么相同的地方?(都是正方形;都可以用4×4來表示等)
(3)你更喜歡哪一個圖形,為什么?(更容易計算;在這個圖形中既可以用4×4表示,也可以表示為 1+3+5+7)
(4)請學生上來指一指 1、3、5、7 分別在哪里;4×4 在哪里?
小結:它們都表示了邊長為4的正方形里小正方形的總個數,得到等式:
1+3+5+7=42。
3.引發思考:如果把拼成的正方形變小一些呢?變大一些呢?
重點反饋1+3+5+7+9=52。
(1)你想到了一個怎樣的正方形?(邊長為5)
(2)畫一畫,跟邊長是4的正方形相比,增加的在哪里?(增加了9,約定把這個像拐角的數叫做“拐角數”)

圖4
(3)隨后依次得到:
1=12
1+3=22
1+3+5=32
1+3+5+7=42
1+3+5+7+9=52
1+3+5+7+9+11=62
……
學生自由表述規律,小結得出:連續奇數相加,有幾個加數,就是幾的平方。
5.引發沖突:3+5+7是否就等于32呢?
逐步完善,準確地表述規律:從1開始,連續奇數相加,有幾個加數就等于幾的平方。
【設計意圖:通過操作活動和觀察思考,引導學生發現數與形之間的規律,通過推理得到一般性結論,并進行準確表述。】
二、運用規律,解決問題
第一層次:1+3+5+7+……+()=202
通過本題的解答,引導學生體驗到運用剛剛發現的規律依次數到第20個奇數比較麻煩,而結合圖形,就會發現拼成后的大正方形邊長與最外層“┓”部分個數之間的關系,即┓=邊長×2-1。有了這條捷徑,就能根據邊長求出正方形最外層“┓”部分的數量,感受到數形結合方法的奇妙,加深學生對數形結合思想價值的感悟。
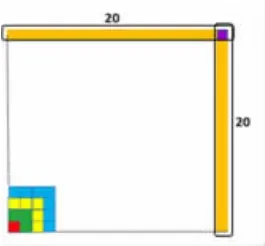
圖5
第二層次:1+3+5+7+……+2017=()2
高等職業院校教師應該采取主動學習和系統完善的策略,借用大數據這一平臺了解和掌握當前在高職教育層面先進的教育教學方法,在提升教學方法多元性和功能性的前提下提升自身的教育教學質量。慕課、微課是當前高等職業院校中較為流行的教學形式,對于教師來講要強化多元化先進教學形式和方法的應用,通過應用掌握慕課和微課等先進方法的開展形式與應用技巧,擴大高等職業院校教育教學的影響范圍,進而為教育教學質量和效果的提升提供方法上和形式上的支持與保障。
在上一題解答的基礎上,繼續借助對圖形的想象與思考,逆向思考,根據正方形最外層“┓”部分的數量求出拼成后的大正方形的邊長,(2017+1)÷2即 2017加了1之后才是兩條完整的邊長,以形助數,直觀簡便。
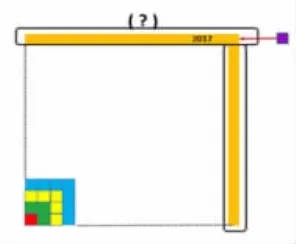
圖6
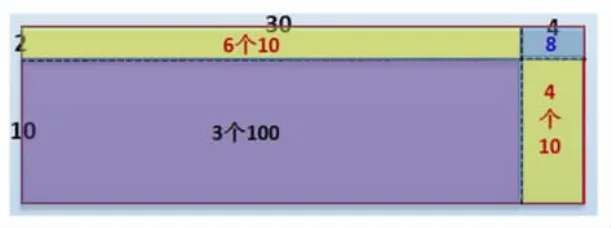
第三層次:1002-992=( )
進一步鞏固和深化對規律的認識,讓學生感受到解決這樣的問題,借助圖形來想象和思考是一條簡便的策略,邊長為100的正方形中去掉一個邊長為99的正方形,剩下的部分就是邊長100的正方形最外面的┓!數形結合,問題就變得簡單了!
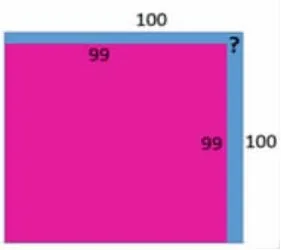
圖7
【設計意圖:進一步深化認識數與形之間的聯系,巧妙地運用數形結合使復雜的問題簡明化,解決起來更加簡單,讓學生進一步體會數形結合的奇妙與優越性。】
三、深化認識,感受價值
1.回顧過去學習過程中數形結合的例子。

【設計意圖:讓學生體會到有了“數”的幫助,判斷“形”時更加準確。】
2.知識拓展,感受運用數形結合理解印度乘法算理。
(1)出示印度人的乘法豎式,跟我們有什么不一樣?(只有結果,沒過程)
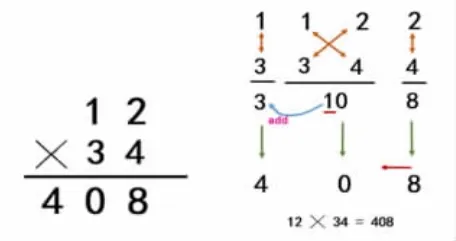
(2)繼續出示:現在能看懂他們是怎么想的嗎?(大部分學生看不明白,適時借助圖形來理解印度乘法的算理)
【設計意圖:通過這個例子,讓學生進一步體會到數形結合是一種常用的數學思想方法。】
四、課后挑戰,鞏固新知
出示97×96巧算過程,學生理解困難,自然想到借助圖形幫助理解,由此布置課后作業:借助圖形探究算理。
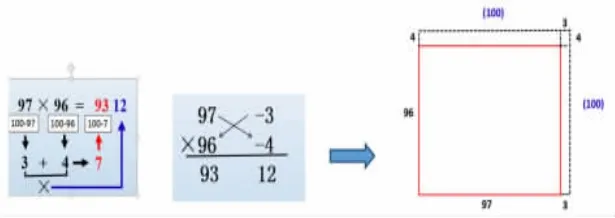
【設計意圖:從一開始老師領著大家一起理解,到后來給出半成品的圖讓學生試著理解,再到最后由學生自主產生“以形助數”想法,由扶到放,舉一反三,使學生認識到,數形結合并不只是這一課的任務,而是整個數學學習過程中重要的思想和方法,從而使數形結合的價值和思想在學生心中真正扎根。】
【教學思考】
2018年2月“嘉興市小學數學六年級上冊期末檢測卷”中一道試題(如下圖):

筆者對所在學校六年級三個班做了抽樣調查,發現學生該題的得分率較低,數形結合不僅是一種解題方法,更是一種重要的數學思想,如何讓學生在數學學習中體驗數形結合思想,最終自覺地運用這種思想解決生活中的問題才是最根本的目標。由此,也引發了筆者對《數與形》一課的重新思考。
1.把握《課程標準》定位。
《課程標準》指出“數學是研究數量關系和空間形式的科學”。個人認為概括起來就是“數”與“形”的問題,通過幾何直觀可以幫助學生建立數的概念、理解數運算的意義,使解題思路與過程具體化。數形結合的方法可以讓數量關系與圖形的性質問題很好地轉化。
2.研讀教材意圖。
《數與形》是修訂版教材新增的內容。實驗教材中,本內容以及后面編排的幾道習題是供學有余力的學生學習和挑戰的。現在作為例題編寫,在教學中究竟該達到怎樣的要求呢?縱觀前面的教材,數形結合思想只是作為幾何直觀一條隱性線索加以滲透,并沒有出現系統的教學,所涉及的練習也比較分散。到了六年級教材專門安排《數與形》一課,個人覺得是對“數形結合”這個數學思想方法的回顧和梳理,進一步讓學生感受到“數形結合”思想方法的重要價值,提高學生用數形結合的思想解決問題的能力。
3.分析學生學情。
回顧學生五年多的學習,他們已經有了一些結合“形”來分析問題的基礎。比如通過幾何直觀建立數的概念、理解運算的意義、明白解題的思路等等。因此,在進一步引導學生體會數與形之間聯系的基礎上,有必要引導學生回顧“數形結合”的內容,進行溝通,求得聯系,在此基礎上獲得新的發展。
本課的重點應是使學生能自覺借助圖形來解決相關數的問題,因此可把目標定為:使學生通過自主探究發現圖形中隱藏著的數的規律,并能準確地表達規律和靈活地運用規律;使學生能自覺借助圖形來解決相關數的問題;使學生在解決問題的過程中,體會數形結合的價值,掌握數形結合、歸納推理等基本的數學思想方法。而探究發現圖形中隱藏著的數的規律,并能靈活地運用規律是需要突破的難點。

