基于Bayes理論現場點荷載強度的判斷

彭 杰

(珙縣宏能芙蓉煤礦有限責任公司, 四川 宜賓市 644500)

0 引 言

巖體是一種變異性很大且不穩定的介質，是受環境影響較大的非均質各向異性體。采礦、隧道等各種地下空間的建設都是在巖土體中進行的，在進行施工前，都必須要詳細準確的了解不同環境下巖石力學參數和巖體力學參數。然而，巖石作為非均質的復雜介質，要想獲得精確的巖石力學參數比較困難，特別是隨著采礦行業的發展，逐漸進入深部采礦作業，面臨復雜的環境，為巖石力學試驗的取樣帶來了很大的困難，不僅僅是費用高，且實驗周期比較長。為了能方便的獲取現場原位巖石的強度參數，必須進行現場巖石強度實驗。現場點荷載強度測試的應用與推廣為現場原位的強度參數測定提供了技術支持。但是，由于現場點荷載強度的試驗樣品是現場隨機拾取的，并且試驗數量有限，造成實驗結果隨機性和不穩定性很大，因此為了確定現場點荷載試驗結果的可靠性，本文利用已有的實測數據獲得巖石現場點荷載強度的概率分布，對小樣本數據進行Bayes方法優化，以提高現場點荷載強度測試結果的可靠性和準確性[5-8]。

隨著Bayes理論在巖土工程方面的廣泛應用，眾多學者也進行了這方面的研究。嚴春風[1]等人應用Bayes理論在有限的小樣本前提下有效的解決了巖石力學參數概率分布的優化問題。畢忠偉[2]等人應用Bayes理論在少量的樣本數據前提下，利用驗前信息對巖石力學參數進行Bayes估計,并首先對其進行可信度研究。鄧建[3]等人指出,破壞性試驗必須運用序貫分析方法或者Bayes方法確定可靠性。閆春嶺[4]從Bayes計算原理出發，結合巖石抗壓強度分布的已有信息，隨機抽取小樣本數據，得到了巖石抗壓強度后驗分布統計量的計算公式，并進行了工程檢驗。筆者結合相關現場實驗數據，應用Bayes方法來判斷現場點荷載強度的概率。

1 Bayes統計原理[4]

Bayes統計學將未知的參數看作隨機變量,并且認為在獲得樣本數據前也已存在一個概率分布,即驗前分布[9]。樣本數據下未知參數的分布稱為后驗分布, 后驗分布是對未知參數統計推斷的依據，因此Bayes方法用于估計某隨機變量的參數，可基本解決樣本容量有限的問題[9]。本文對后驗概率密度進行理論計算。

假設現有現場測試樣本A1，A2，…，An出自于未知的整體樣本A，并設F(ai，Q)是A的分布函數，樣本的分布函數如下：

(1)

在Bayes估計中，θ是取值于參數空間Θ的一個隨機變量，分布函數式(1)實際就是隨機變量θ為某一特定值條件下的樣本的分布情況，因此，式(1)可被改寫為：

(2)

(3)

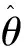
g(a1，a2…an，θ)=g(a1，a2，…，an|θ)h(θ)

(4)

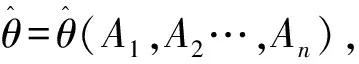
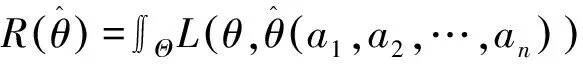
(5)

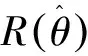
(6)

稱之為θ的Bayes估計。

令右式為0，交換積分次序，并利用式(4)得：

(7)

令:

(8)

其中，

(9)

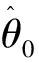
2 Bayes方法在現場點荷載強度中的應用

(10)

式中，i=1,2，…，n，式(10)即是式(9)在離散狀態下的Bayes公式。式(10)中{p(A1)，p(A2),…,p(An)}稱為驗前分布，B為發生的事件；P(Ai|B),i=1,2,…,n為驗后分布，綜合了前信息和試驗所提供的信息[9]。

由于對巖石強度的試驗價格昂貴，時間周期長，且取樣比較困難，人們總是希望通過少量的實驗來獲得準確而大量的信息。特別是現場點荷載強度的測試，其取樣源于現場隨機取樣，并且試樣的形狀和尺寸也是帶某一范圍內隨機的。現場點荷載強度測試本身就是一個隨機性的測試，因此對現場少量的試驗數據進行Bayes判斷顯為重要，特別是隨著Bayes方法在巖土工工程中的應用越來越廣泛。現以現場點荷載強度為例，現場點荷載強度為一隨機變量，用X表示，X1，X2，…,Xn為X的樣本，這種隨機變量X樣本可視為正態分布，即X～N(μσ2)，設小樣本計算出的均值和方差分別為ν和τ2，則可求出在二次損失函數下μ,σ2的Bayes估計：

(11)

(12)

3 工程實例

以現場點荷載測試為基礎，通過少量的現場點荷載強度測試來驗證Bayes法在點荷載強度方面的適用性。點荷載強度測試采用SD-1數碼點荷載儀。點荷載試樣通過現場拾得，取樣要求長寬不超過10 cm，由于現場條件的限制，選擇能滿足儀器的巖樣都可以。這次所選擇的巖樣長寬主要在小于15 cm的塊狀巖塊，加荷間距以30～50 mm為宜，考慮到現場的條件限制，試樣的加荷間距為40～60 mm的巖塊，巖塊試樣如圖1所示。39組現場點荷載強度測試數據(見表1)。現場點荷載測試試件本身就是隨機性的測試。因此，樣本完全服從正態分布。樣本均值μ=3.29，σ2=4.49。即先驗分布服從N(3.29，4.49)。

圖1 巖塊試樣

在表1中隨機取5個數據組成一組，并且隨機取4組，如表2所示。計算出的均值方差也如表2所示。通過Bayes方法估計即式(11)和式(12)計算所獲得的均值和方差如表2所示。計算值和樣本誤差值計算見表3，由表3可知誤差基本都小于10%，說明后驗分布的均值和方差與總體樣本的均值和方案值比較接近，因此Bayes方法適合用于現場點荷載強度的估計。

為了進一步說明上述小樣本Bayes統計方法的適用性，再隨機取4組數據，每組7個，對Bayes統計方法的適用性進行驗證，如表4所示。

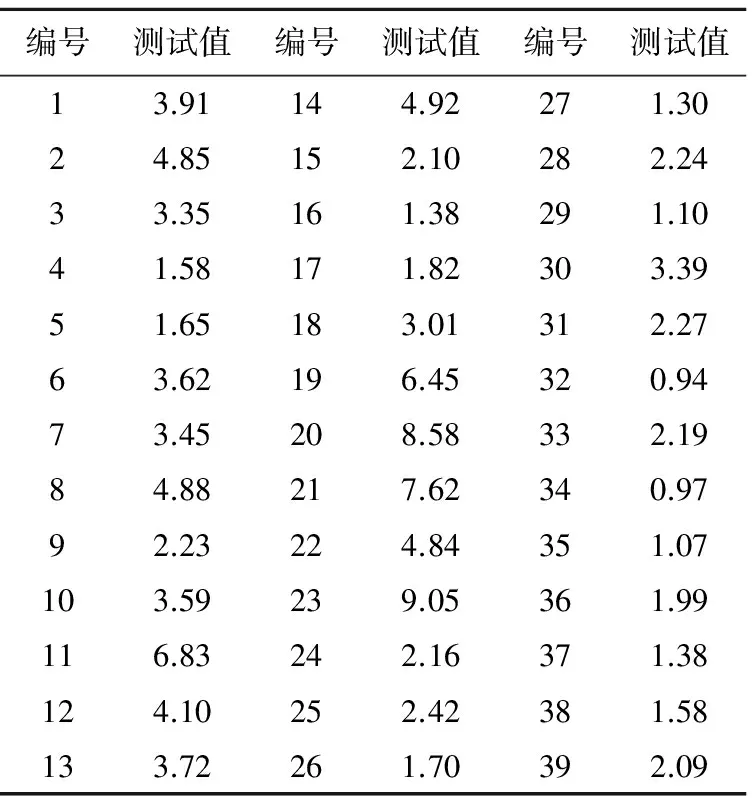
表1 現場點荷載強度測試結果

表2 隨機抽取計算均值和計算方差

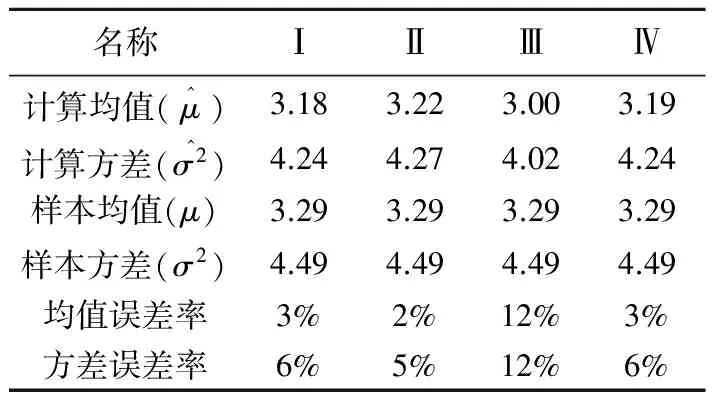
表3 計算值和樣本值誤差計算結果

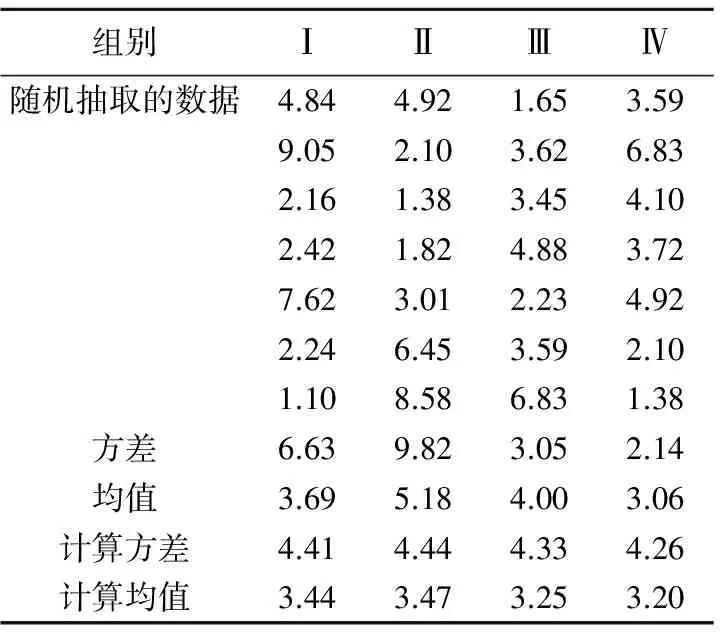
表4 隨機抽取計算均值和計算方差

計算出的均值方差也如表4所示。通過Bayes方法估計即式(11)和式(12)計算所獲得的均值和方差由表4所示。表5所示的計算值與樣本值誤差全部都小于10%，如表5所示，說明后驗分布的均值和方差與總體樣本的均值和方案值比較接近，因此Bayes方法適合用于現場點荷載強度的估計。

因此，在礦山需要獲得巖體或巖石的強度參數時，可以利用本方法通過少量的試驗數據來獲得比較準確的巖石或巖體力學參數。

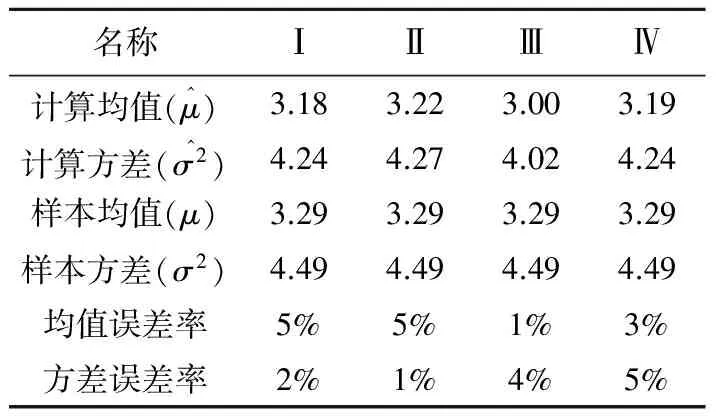
表5 計算值和樣本值誤差計算結果

4 結 論

本文根據現場點荷載強度測試的特殊性，即試樣尺寸、形狀都不規則，并且試樣的采集都是現場隨機拾取。針對這些特點，從Bayes原理出發，針對現場點荷載強度測試的已有的少量樣本信息，通過隨機取樣計算出現場點荷載強度后驗分布統計量的計算公式，分析了Bayes統計方法在現場點荷載強度測試領域方面的應用。并對其可靠性和計算誤差做了詳細的統計，統計結果表明，利用Bayes方法對現場點荷載強度進行概率分布參數的計算，能夠通過小樣本數據，獲得巖石現場點荷載強度的概率分布，具有較高的實用價值。但是值得注意的是，該方法必須建立在數據搜集形成的大樣本基礎上，否則結果沒有實際意義[4]。

參考文獻：

[1]嚴春風,陳洪凱,張建輝.巖石力學參數的概率分布的Bayes推斷[J].重慶建筑大學學報,1997,19(2):65-71.

[2]畢忠偉,丁德馨,饒 龍,等.巖石參數Bayes估計中驗前樣本可信度的研究[J].水利學報,2006,37(8):1000-1003.

[3]鄧 建,李夕兵,古德生.巖石力學參數概率分布的信息熵推斷[J].巖石力學與工程學報,2004,23(13):2178-2181.

[4]閆春嶺.巖石抗壓強度的Bayes推斷[J].山東科技大學學報(自然科學版)，2012,31(4).

[5]光耀華.巖石抗剪強度指標的概率分析[J].巖石力學與工程學報,1994,13(4):349-356.

[6]蔣樹屏.擴張卡爾曼濾波器有限元法耦合算法及其隧道工程應用[J].巖土工程學報,1996,18(4):11-19.

[7]徐 軍，雷 用，鄭穎人.巖土參數概率分布推斷的模糊Bayes方法探討[J].巖土力學,2000,29(4):88-91.

[8]楊 坤.模糊方法在煤礦區矸石山可靠性分析中的應用[J].山東科技大學學報(自然科學版),2010,29(4):88-91.

[9]畢忠偉.巖體力學參數推斷的Bayes方法及截尾可靠度的研究與應用[D].長沙：中南大學，2008.