基于核主成分分析和粒子群優化支持向量機的統計數據缺失值插補
吳桐雨,吳少雄
(1.福州大學 經濟與管理學院,福州 350116;2.福建工程學院 交通學院,福州 350118)
0 引言
現有統計數據因各種原因存在缺失值,給統計分析帶來一定的困難。通常采用刪除缺失的單元項進行統計分析,然而這種做法會丟失有用的信息,容易得出誤導性的結論。插補技術能夠為缺失項確定一個合理的數值,減小由數據缺失帶來的估計偏差,完善統計數據集利于后期操作。
常用的插補方法有演繹估計、均值插補、隨機插補、回歸插補和多重插補、極大似然估計、EM算法等;李序穎考慮空間相關性引入空間自回歸模型;張松蘭提出統計方法與機器學習相結合的支持向量機、神經網絡和決策樹方法[1];其他方法還有最近鄰插補法和關聯規則法、得分匹配法等。其中,單值插補的不足在于根本上改變了數據的原始分布,造成抽樣誤差,且不能很好地體現出缺失值的不確定性。空間自回歸模型需要驗證數據間的相關性,對相鄰缺失值的插補可能存在一定的偏差,難以處理大量的缺失數據。研究表明,通過學習相關度較大的已知屬性值進行估計的精度更高[1],用支持向量機方法對數據進行插補較傳統方法有更高的恢復率[2]。總的說來,采取以上方法處理數據缺失存在各自的優勢,但也有其不足之處,比如一些研究僅適用于小樣本情況下的插補,對于大樣本插補的精度有所下降;一些研究雖然考慮了數據間的影響關系,但考慮的因素并不全面;大部分文獻集中于研究社會調查中的數據缺失插補方法,鮮有文獻研究統計數據的缺失插補方法,而且插補的精度還有待進一步改善。支持向量機作為一種新興的統計學習算法在模式識別、回歸估計等方面均取得理想效果,本文以福建省流通產業的統計數據為例,將核主成分分析、粒子群算法和支持向量機三者有機結合,對統計數據的缺失值進行插補。
1 模型原理
1.1 核主成分分析(KPCA)
核主成分分析是通過一個非線性變換將數據從輸入空間投影到高維特征空間,然后在高維空間進行線性主成分分析,其中,非線性變換通過定義內積函數實現,該函數由一個核函數代替。這種方法可以避免單純使用線性主成分分析遇到的特征向量線性不可分的問題[3]。

根據 λν=Cν,求C的特征值 λ及特征向量V∈F{0},C的特征值非負。設C的特征值為0≤λ1≤λ2≤…≤λn,對應的特征向量為 ν1,ν2,…,νn。記:

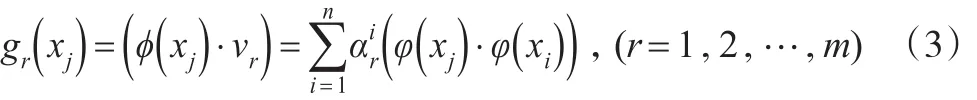
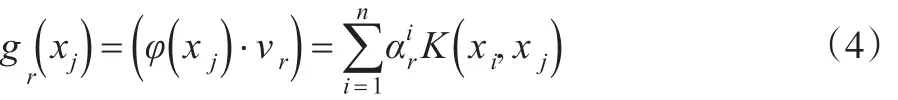
在實際操作中,可以根據一定的規則選取式(4)的前幾個分量作為主成分。
1.2 粒子群優化(PSO)
粒子群優化是一種智能群體搜索方法,其基本思想是初始化為一群隨機粒子,每個粒子代表解空間的一個候選解,粒子通過跟蹤個體最優值和全局最優值來更新自己的速度和位置,迭代直至達到預先設定的目標則實現最優解[4]。粒子通過以下兩個公式更新其位置和速度:
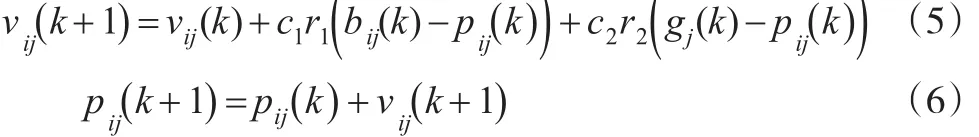
式中,k為進化代數,νij(k+1)為粒子i在第k次迭代中第j維的速度,νij∈[ ]-νmax,νmax,νmax是粒子被允許移動的最高速度;c1,c2是加速系數,通常取值為2;r1,r2是[0,1]之間的隨機數;pij是粒子i在第j維上的個體極值點的位置,pij∈[ ]-pmax,pmax,pmax是粒子被允許移動的最大位置;gj是整體在第j維上的全局極值點的位置。設搜索空間的第j維定義為區間 j∈[ ]-pjmax,pjmax,則通常有
1.3 最小二乘支持向量機
最小二乘支持向量機的基本思想是通過非線性變換將數據映射到高維特征空間,并構造最優決策函數,利用原空間的核函數代替高維特征空間中的點積運算,用有限樣本的學習訓練來獲得全局最優解[5]。
對于給定的樣本數據,作非線性映射Φ:Rn→F,則被估計函數 f(x)為:

在權w空間中的函數估計描述為以下求解問題:
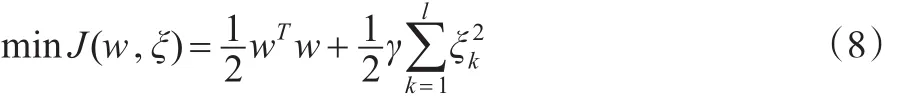
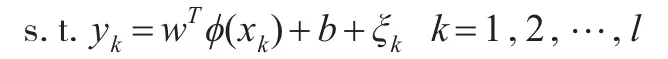
其中:w為空間F中的權向量,b∈R為偏置,誤差變量ξk∈R,b是偏差量,γ是可調超參數。
根據式(8),可定義拉格朗日函數:
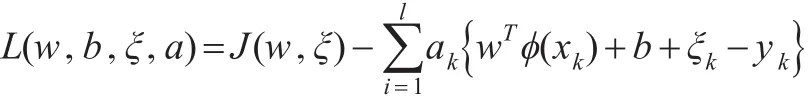
其中,拉格朗日乘子ak∈R。對上式各變量求偏導并整理線性方程組:

最小二乘支持向量機的函數估計為:

其中,a、b由式(9)求解出。不為零的ai對應的樣本為支持向量。
2 流通產業統計評價指標與數據
在研究省域流通產業評價指標體系中,將評價指標分為6個一級指標,22個二級指標,45個三級指標[6],具體見表1。
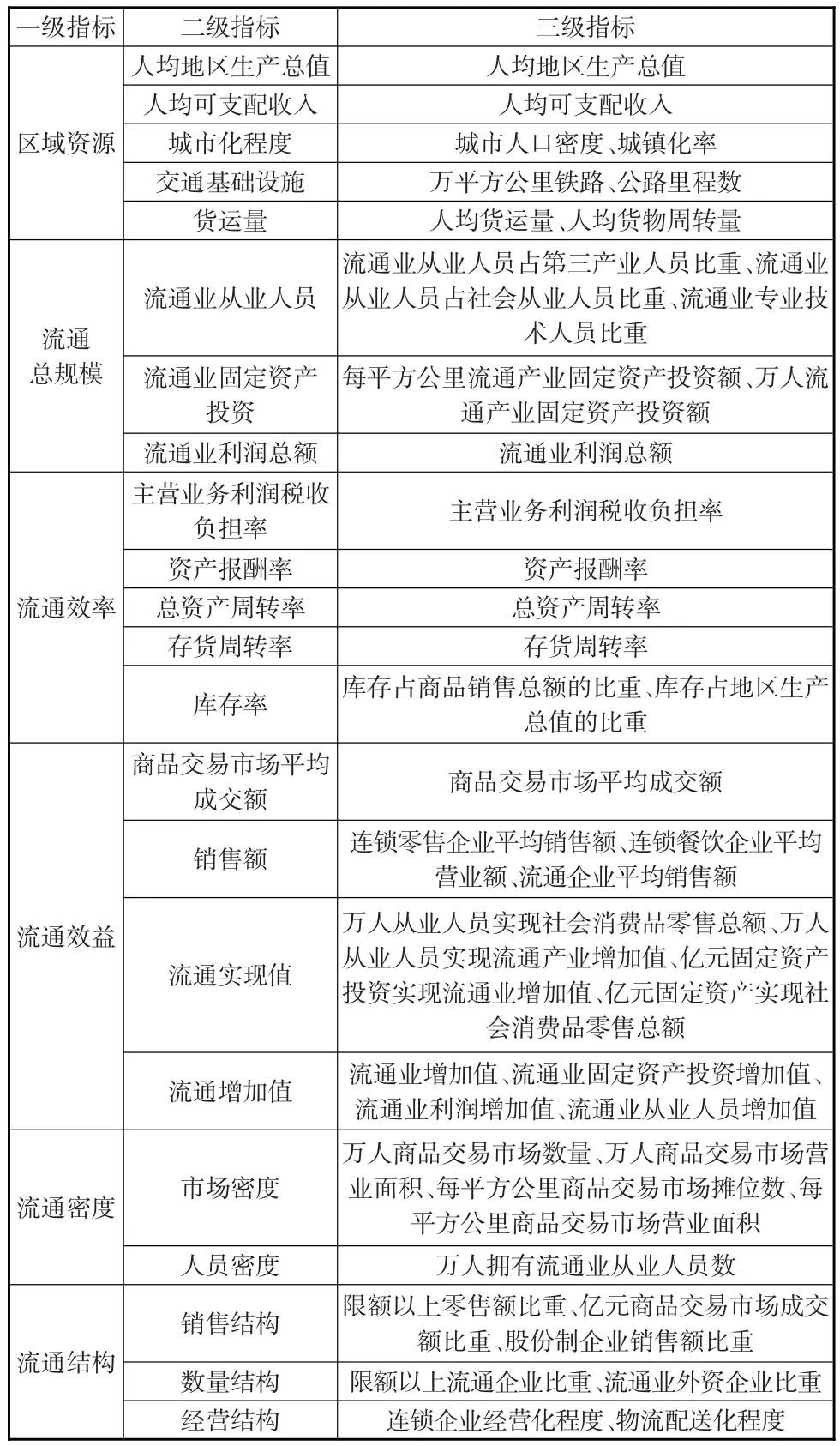
表1 省域流通產業競爭力評價指標體系
由于我國對流通產業的統計并沒有統一的口徑,而是分散在批發業、零售業、餐飲業、交通運輸、倉儲和郵政業幾個行業中。本文共收集了各省從1949—2015年85項統計指標的數據,數據來源于《中國統計年鑒》、《中國貿易外經統計年鑒》、《中國第三產業統計年鑒》等。其中,1949—1991年和2015年統計數據缺失較多,1992—2014年存在少量缺失值,若將含有缺失數據的年份全部剔除后進行分析,將會丟失大量有用的信息,對流通產業競爭力的評價可能會出現誤導性的結果。因此,選取1992—2014年含有缺失值的福建省流通產業相關統計數據為例進行數據插補研究。
3 統計數據缺失值插補
3.1 統計數據缺失值插補過程
統計數據缺失值插補的詳細流程如下:
(1)為增加樣本集和提高數據修補的準確性,采用增量變化的方法進行數據處理,即將各年份的數據相減所得作為訓練與測試的樣本,這樣23年的統計數據共產生132組數據。
(2)因各項統計數據存在較大差異,且量綱不一致,需對數據進行預處理,使它們統一歸一化到-1~1。
(3)選取有數據缺失的指標作為研究對象,采用高斯徑向基核函數,對其余的44項統計指標進行核主成分分析。主成分累計貢獻率如圖1所示,其中第1主成分貢獻率為0.266,第2主成分累計貢獻率達0.448,第13主成分的累計貢獻率為0.908,選取前13個主成分作為最小二乘支持向量機的新影響因子。
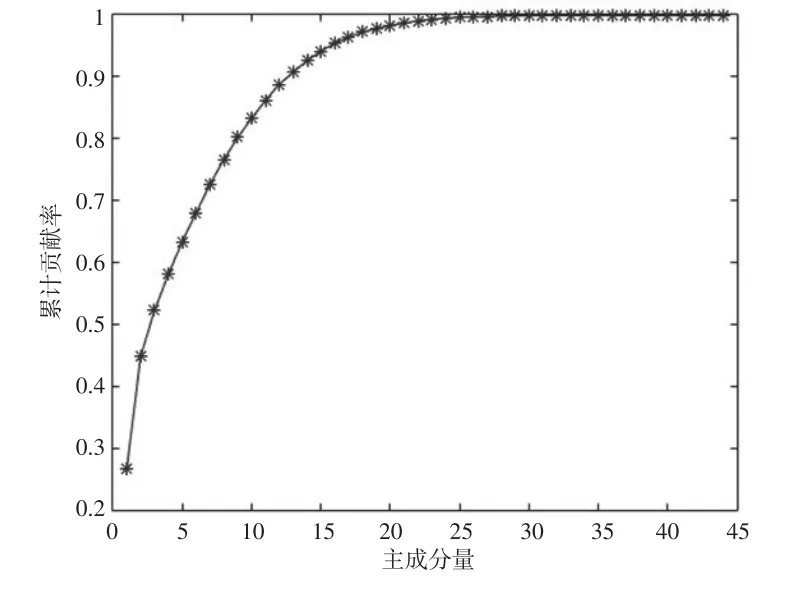
圖1 主成分累積貢獻率
(4)將新影響因子和數據缺失指標的數據分成兩部分,前100組數據作為訓練樣本,后32組數據為測試樣本。
(5)應用PSO優化最小二乘支持向量機的超參數,加速系數c1.c2均設為2,慣性權重w設為0.6,種群規模設為20,最大迭代步數設為100。搜索得到支持向量機的參數懲罰因子=3124.8795和RBF核函數參數=20.5206。
(6)應用最小二乘支持向量機對樣本分別進行訓練和測試,測試結果如圖2和表2所示。
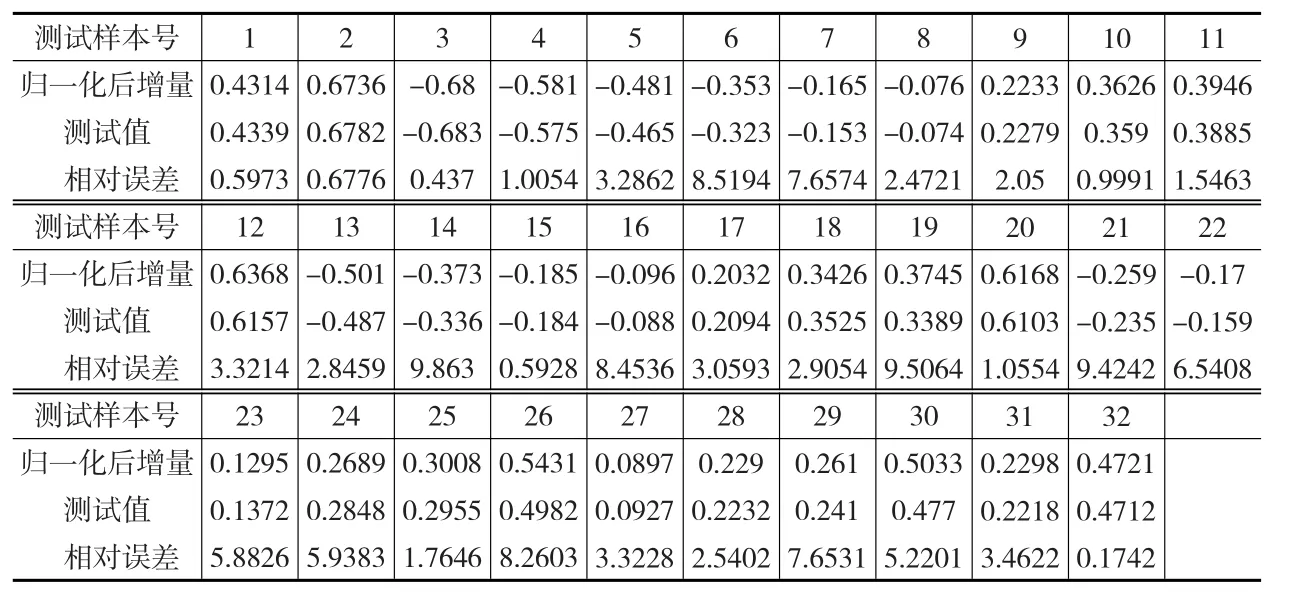
表2 測試結果分析
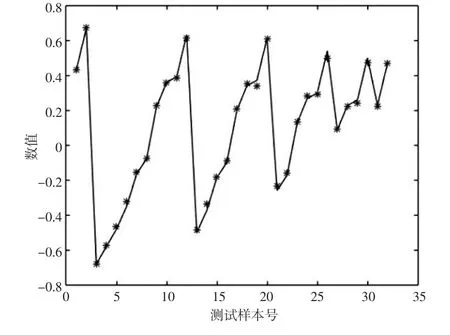
圖2 模型測試值與真實值比較
3.2 測試結果分析
由表2可以看出基于核主成分與支持向量機的方法進行數據插補可以取得較好的效果,最大相對誤差為9.863%,最小相對誤僅為0.1742,平均相對誤差為4.094%。
4 結論
在開展統計數據分析時,對缺失數據進行插補是十分必要的。將核主成分分析與支持向量機模型結合,建立數據插補模型,具有很好的非線性信息提取和降噪的能力,研究表明其具有較高的精度,可以應用于數據插補。
參考文獻:
[1]張松蘭,王鵬,徐子偉.基于統計相關的缺失值數據處理研究[J].統計與決策,2016,(12).
[2]張嬋.一種基于支持向量機的缺失值填補算法[J].計算機應用與軟件,2013,30(5).
[3]Scholkopf B,Smola A J,Muller K R.Kernel Principal Component Analysis[M].Massachustees:MIT Press,1999.
[4]楊維,李歧強.粒子群優化算法綜述[J].中國工程科學,2004,6(5).
[5][美]瓦普尼克.統計學習理論的本質[M].北京:清華大學出版社,2000.
[6]張連剛.省域流通產業競爭力評價體系構建與實證研究[D].成都:西南財經大學博士學位論文,2011.

