GM(2,1)模型時間響應系數的優化方法
蘇海軍,邵 藝
(西華師范大學 數學與信息學院,四川 南充 637002)
0 引言
灰色系統理論自誕生以來,已經廣泛的應用于社會、經濟、管理、農業、醫學等多個領域。作為其核心內容的灰色模型更是應用廣泛,并取得了較好的效果。對于GM(2,1)模型,劉思峰等在文獻[1]中詳細給出了的定義及建模方法,并作了一定的應用。但是,原始GM(2,1)模型仍然存在著不足,主要體現在兩方面:第一方面,從作為模型定義的灰微分方程跨越到求解時間響應式的白化微分方程缺乏嚴格理論依據,存在一定不合理性,從而導致兩個方程不夠匹配;第二方面,時間響應式中的兩個初值是在強行指定第一個時間點和最后一個時間點的模擬值與真實值相等的條件下確定的,缺乏合理性。目前,對GM(2,1)模型的修正方法不多,文獻[2]利用最小二乘法改進GM(2,1)模型算法及其預測步驟,用MATLAB實現了預測;文獻[3]利用權值對一階灰導數和背景值進行加權組合,對GM(2,1)模型進行了改進;文獻[4]利用最小二乘法與數值試驗的方法對GM(2,1)模型進行了改進;文獻[5]提出了累積法GM(2,1)模型并對其病態性做了一定的研究,文獻[6]利用微粒群算法將GM(2,1)模型拓展為 GM(2,1,λ,ρ)模型,在一定程度上提高了GM(2,1)模型的模擬精度。
本文將對時間響應式中的兩個常數的確定給出較為合理的方法。在文獻[1]中,GM(2,1)模型時間響應式中的兩個初值是在強行指定第一個時刻點和最后一個時刻點的模擬值與真實值相等(即)條件下確定的,中間時刻點對初值的確定就沒有起到任何作用,這樣就造成對信息利用不夠充分。理想的響應系數(c1,c2)應滿足,然而這是不可能的,所以本文采用各個擊破的方法,對正整數i,j(1≤i≤n-1,i<j≤n),尋求滿足,然后利用Lingo軟件再求滿足最小的 (c1,c2),通過實例驗證,表明此法確定的相應系數預測精度較高。
1 基本概念
定義1[1]:設原始序列其1-AGO序列為,1-IAGO序列,其中,緊鄰均值生成序列為。稱:
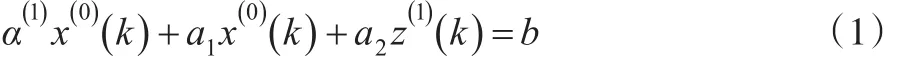
為GM(2, 1) 模型(其中k=2,3…n);稱:

為GM(2, 1)模型的白化方程。
定理1[1]:設 X(0),X(1),Z(1),α(1)X(0)如定義1所述,且:
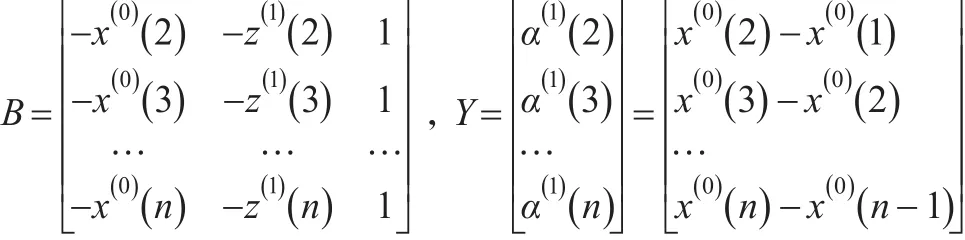
則:
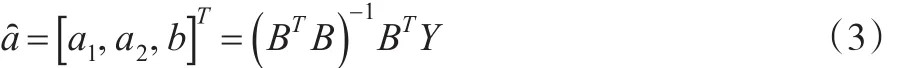
定理2[1]:關于GM(2,1)模型白化方程的解有以下結論:
結論1:設 X(1)*是方程(2)的特解,ˉ(1)是對應齊次方程的通解,則是GM(2,1)模型白化方程的通解。

當特征方程r2+a1r+a2=0有兩個不相等的實根r1,r2時:

當特征方程r2+a1r+a2=0有兩個相等的實根r時:

當特征方程有r2+a1r+a2=0兩個共軛復根r1=α+βi,r2=α-βi時
其中,c1,c2由方程組確定。
結論3:白化方程的特解X(1)*有以下三種情況:

2 確定GM(2,1)模型時間響應式中常數c1,c2的新方法
設 X(1)*是白化方程(2)的特解ˉ(1)是對應齊次方程(4)的通解,則是模型白化方程的通解。下面分三種情形討論:
情形1:當a1=a2=0時,0是特征方程r2+a1r+a2=0的重根,即r1=r2=0。
設 X(1)*=Bt2,代入白化方程得B=b,即 X(1)*=bt2,此時:

因此:
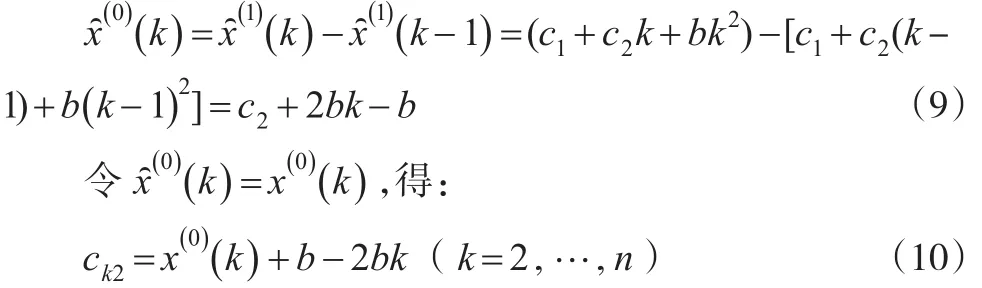
情形2:當 a2=0,a1≠0 時,0是特征方程 r2+a1r+a2=0的單根,不妨設r2=0,則r1=-a1。
設 X(1)*=Bt,代入白化方程得此時:

因此:
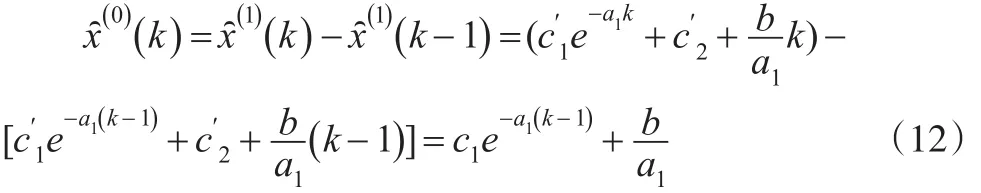
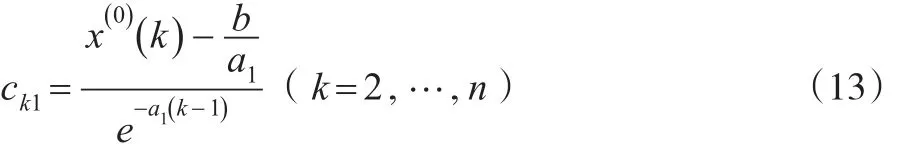
說明:此情形為DGM(2,1)模型。
情形3:當a2≠0時,0不是特征方程r2+a1r+a2=0的根,設,代入白化方程得,此時根據特征根的結果有以下三種情況。
情形1:當特征方程r2+a1r+a2=0有兩個不相等的實根 r1,r2時:

因此:
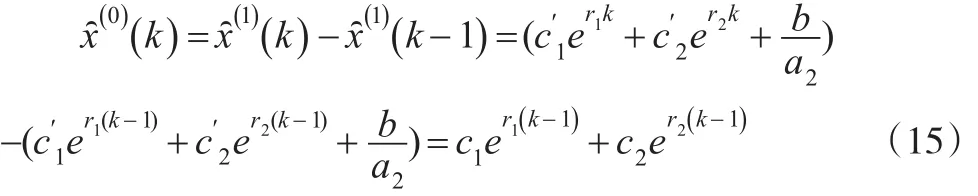
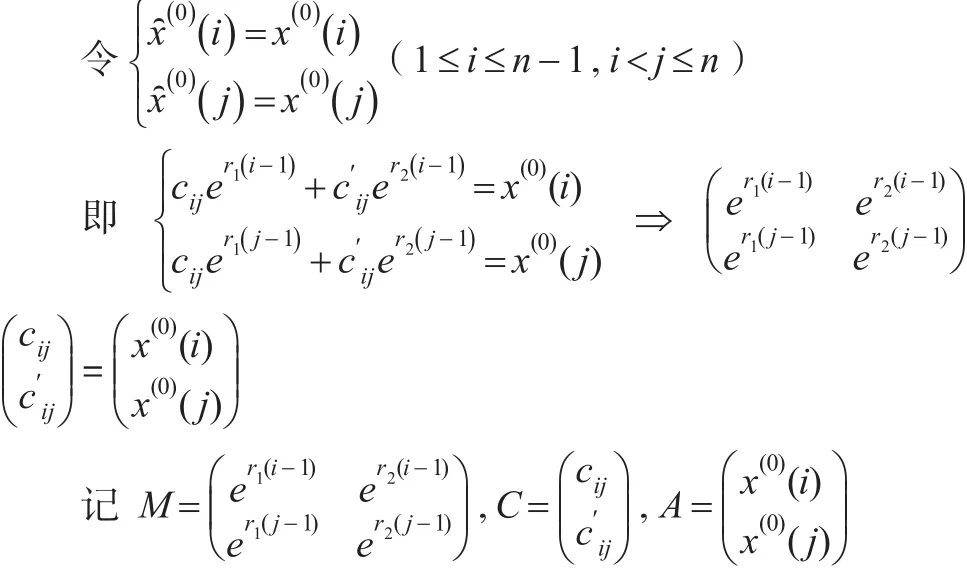
情形2:當特征方程有兩個相等的實根r1=r2=r時:

因此:
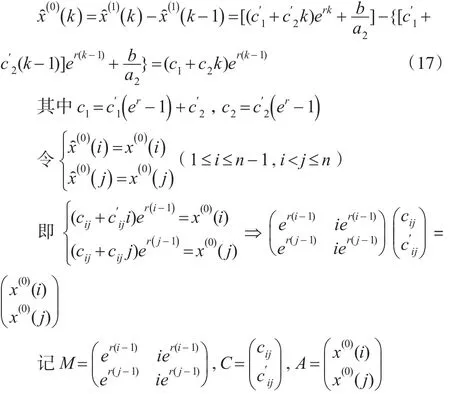
即MC=A,所以C=M-1A,由此得出再利用情形1的方法求得c1,c2。
情形3:當特征方程有兩個共軛復根r1=α+βi,r2=α-βi(僅此處i為虛數單位)時:
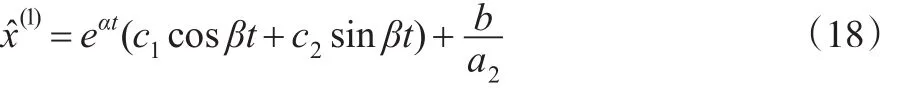
所以:
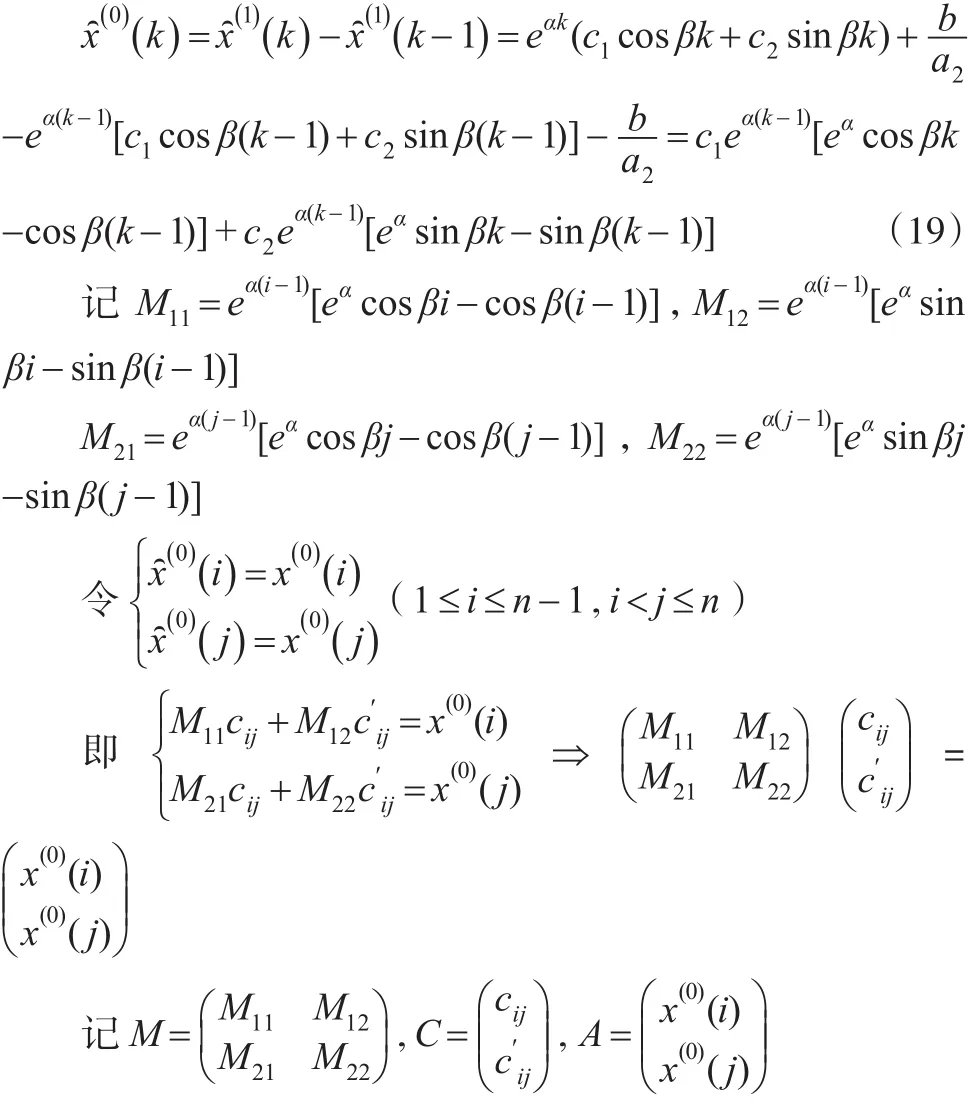
即MC=A,所以C=M-1A,由此得出
再利用情形1的方法求得c1,c2。
3 模型應用與比較分析
以文獻[1]第174頁的數據序列:X(0)=(2.874,3.278,3.337,3.39,3.679)為基礎建立GM(2,1)模型。
按本文方法推導預測公式:
X(0)的1-AGO序列和1-IAGO序列分別為:
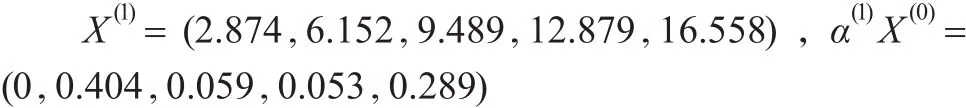
X(1)的緊鄰均值生成序列為:
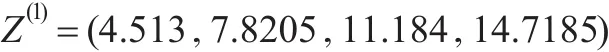
故得GM(2,1)的白化方程:
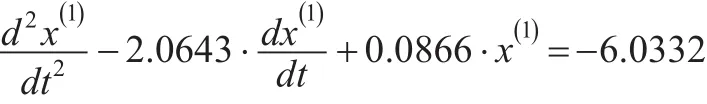
特征方程有兩個不相等的實根r1=2.0215,r2=0.0428,屬于本文情形3的第(1)種情況。
初始值分別為:
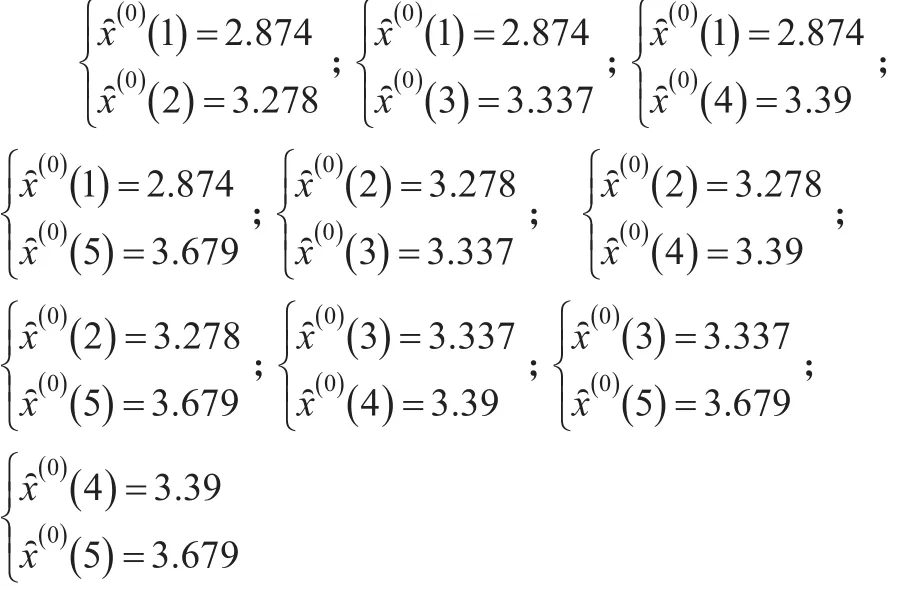

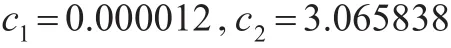
將 r1,r2,c1,c2代入(15)得:
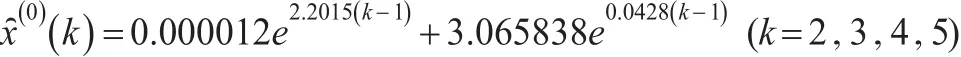
幾種預測方法的精度對比:
文獻[1]GM(2,1)模型、文獻[6]GM(2,1,λ,ρ)模型以及本文GM(2,1)模型的精度檢驗見表1(其中文獻[1]、文獻[6]的計算結果直接取自文獻[1]、文獻[6])。由表1可以看出,按本文所提的方法進行GM(2,1)模型的計算可以得到更好的效果。
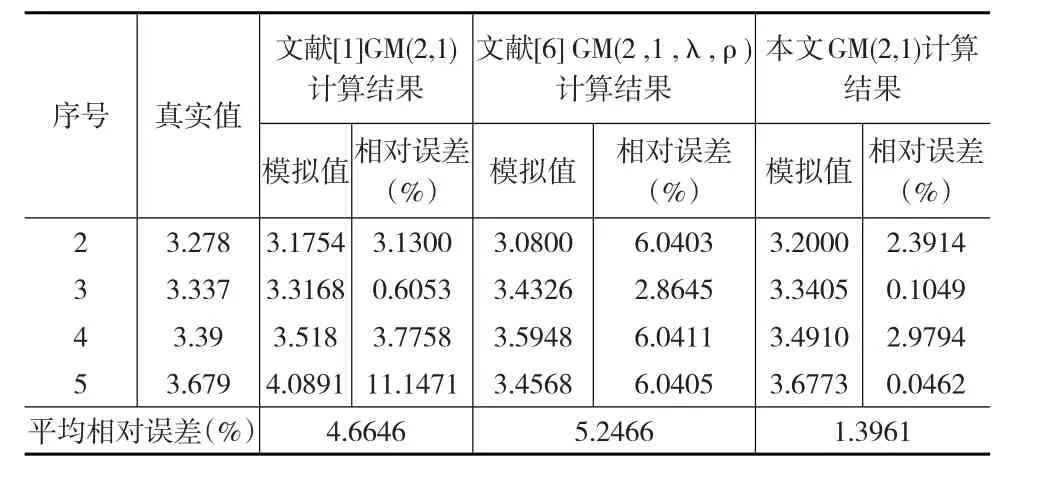
表1 精度檢驗
4 結束語
GM(2,1)模型白化響應式中常數c1,c2的確定直接影響模型的精度,原始GM(2,1)模型的時間響應式中兩個初值是在強行指定第一個時刻點和最后一個時刻點的模擬值與真實值相等的條件下確定的,中間時刻點對初值的確定沒有起到任何作用,造成了對信息利用不夠充分;理想的響應系數 (c1,c2)應滿足這顯然是不可能的,因此本文退而求其次,各個擊破,對正整 數 i,j( 1≤i≤n-1,i<j≤n ),尋 求滿足,然后利用Lingo軟件再求滿足最小的,通過實例驗證,表明此法確定的相應系數預測精度較高。
參考文獻:
[1]劉思峰,黨耀國,方志耕,謝乃明.灰色系統理論及其應用[M].北京:科學出版社,2010.
[2]李玲玲,單銳,崔紅芳.改進GM(2,1)模型的MATLAB實現及其應用[J].數學的實踐與認識,2011,41(20).
[3]牛思先,陳鵬宇,蘇玉剛.基于加權組合最小二乘法改進的GM(2,1)模型[J].統計與決策,2010,(22).
[4]沈繼紅,趙希人.利用最小二乘法改進GM(2,1)模型[J].哈爾濱工程大學學報,2001,22(4).
[5]曾祥艷,肖新平.累積法GM(2,1)模型及其病態性研究[J].系統工程與電子技術,2006,28(4).
[6]劉虹,張歧山.基于微粒群算法的GM(2,1,λ,ρ)優化模型[J].系統工程理論與實踐,2008,10(10).

