數學教科書例題的分類及其教學建議

陸明明

?

數學教科書例題的分類及其教學建議

陸明明1，2

（1．南京市玄武區教研室，江蘇 南京 210016；2．南京市高中數學渠東劍名師工作室，江蘇 南京 210016）

數學教科書中的例題具有基礎性、典型性、層次性、發展性和系統性，可分為Q型和P型兩類．Q型例題是直接利用規則并按照一定程序去完成解答的例題，其功能是使學生形成自動化技能；教學分為3個階段：形成產生式、產生式自動化和形成產生式系統．P型例題是通過建立數學模型完成解答的例題，其功能是獲得策略性知識，形成執行復雜認知操作的產生式系統；教學可以從“弄清問題、分析問題、回顧反思、變式學習”4個階段進行．

例題分類；例題教學；產生式；變式

如何提高數學教學效率是人們一直關注的重要課題．王光明教授指出：“數學教學效率的高低不取決于教師打算教給學生什么，而取決于學生實際獲得了什么．”[1]可見，提高學生的學習效率是數學教學的關鍵．而學生學習效率的提高主要是通過教師有效的教，激發學生的內驅力，促進學生意義學習．例題是學生學習活動的重要內容，如何有效的教例題，嘗試作一些探討．

例題是數學教科書的重要組成部分．李善良博士指出：“教材中的素材要堅持4個字：精、典、新、思．……尤其是數學教材中的例題、練習、習題，必須考慮學生學習心理規律，根據數學運用的不同層次：辨認識別、變式練習、解決簡單問題、解決復雜問題等，選配比較典型的題目，內部自成系統，相互聯系，學生經過這些基本的訓練足可以掌握相關知識與技能，并且這些習題的量是最小的．”[2]可見，數學教科書中的例題是編者精心選配的，具有基礎性、典型性、層次性、發展性和系統性．

數學概念、原理和思想方法都比較抽象，例題就成了學生理解概念、原理，領悟數學思想方法的具體途徑，例題教學也就成為數學教學的基本形式[3]．文[4]從宏觀層面提出數學教科書中的例題具有示范引領、揭示方法、介紹新知、鞏固新知、思維訓練和文化育人等6個功能，具有普適性．例題教學中，有效的教的方式取決于教科書例題的功能定位．如何準確定位教科書例題的功能，需要對教科書例題進行分類．即根據教科書例題的分類，明確不同類型教科書例題的功能，據此確定有效的教的方式．

1 教科書例題及其分類

1.1 從例題的語義上理解

關于“例”．現代漢語詞典解釋如下：“【名詞】①從前有過，后來可以仿效或可作為依據或標準的事物．②用作依據的標準或規則．③例子．④調查或統計時指合于某種條件的事例．【動詞】比照；比類．【形容詞】按條例規定進行的．【副詞】按規定．”古漢語詞典解釋如下：“①類別．②規則，條例．③照例．”

由以上解釋不難看出，例題應該具備4點基本屬性．首先，是一個標準，具有基礎性，強化“近利”（即基本知識和基本技能），融入“遠慮”（即基本思想和基本活動經驗）．其次，是一個比類，具有代表性，代表一類問題．再其次，是一個例子，具有典型性，代表中的代表．最后，是一個照例，不僅具有示范性（模仿的榜樣），而且具有規范性（準確運用數學語言表達）．

1.2 教科書例題的構成要素

例題，現代漢語詞典解釋如下：“為說明某一定理、定律或原理而舉出來用作例子的問題或題目．有時附有具體的解釋．”不難看出，例題的本質是問題（包括題目）．教科書是教與學雙邊活動的最重要媒體[2]，不僅是教師實施創造性教學的重要材料，也是學生學習活動的重要線索．所以，教科書例題不僅包括對問題的陳述，還包括完整的、規范的解答；對于一些綜合性例題，還應給出必要的分析過程．綜上，教科書例題應具備兩個基本要素：問題和解；必要時，附分析過程．

1.3 教科書例題的分類

喻平教授提出了4種數學解題教學模式：“認知建構模式、自動化技能形成模式、模型建構模式和問題開放模式．認知建構模式是指通過系列變式問題的解決，促使學生建立良好的認知結構．自動化技能形成模式是指通過解決直接利用規則并按一定程序去完成解答的問題，促進學生獲得自動化程序性知識．模型建構模式是指通過建立數學模型解決問題，促使學生獲得策略性知識，提高分析問題和解決問題的能力．問題開放模式是指通過開放性問題的解決，促使學生鞏固陳述性知識，發展策略性知識．”[5]不難看出，自動化技能形成模式和模型構建模式中所解決的問題是由本源的數學知識演化而來，而認知建構模式和問題開放模式中所解決的問題是由基本問題變化而來．即由本源的數學知識演化出基本問題，基本問題通過變式、組合可以再生豐富多樣的問題．綜上，基本問題可以分為兩類：一類是直接利用規則并按照一定的程序能完成解答的問題；一類是通過建立數學模型完成解答的問題．

依據上述對基本問題的分類標準，教科書例題可分為兩類：一類是直接利用規則并按照一定的程序去完成解答的例題，稱之為問題解答（Question）型例題，簡稱Q型例題；一類是通過建立數學模型完成解答的例題，稱之為問題解決（Problem）型例題，簡稱P型例題．

參考已有的研究成果[6-11]，兩類例題從時間序列看，Q型例題一般是學生剛剛習得新知后需要解決的例題，先于P型例題出現；從知識點數量看，Q型例題是單一知識點的直接陳述，P型例題是一定背景下多種知識融合的綜合性試題；從要求水平看，Q型例題：模仿、簡單運用，P型例題：綜合運用、探究；從難度看，P型例題的難度高于Q型例題．因此，從5個維度：背景、數學認知、運算、推理和知識綜合分別給出Q型、P型例題的內涵特征，見表1．

表1 Q型和P型例題的內涵特征

1.4 兩類例題的功能

Q型例題是直接利用規則并按照一定的程序去完成解答的例題，其功能是把剛剛習得的陳述性知識轉換為程序性知識，即以產生式表征，并發展為自動化的技能．

P型例題是通過建立數學模型完成解答的例題，其核心功能是獲得問題解決的策略性知識，包括弄清問題的基本策略和解決問題的基本方法，形成執行復雜認知操作的產生式系統．同時，在求解過程中，促使學生多途徑地理解知識，豐富知識節點處的聯系性（這種聯系性是方法產生的源泉），進而發展思維品質．

2 例題學習的相關理論基礎

2.1 產生式遷移理論

產生式最早由Post提出，逐步發展成為一種以操作為中心的知識表征法，被描述為“條件—動作”對．如果行為產生的條件得到滿足，那么執行相應的動作，簡稱C—A規則[12]．產生式也是表征程序性知識的最小單位．之后，Newell和Simon把產生式描述為人類解決問題中的信息加工過程的形式化語言，其基本假設是：人類解決問題的知識可以表示為一系列產生式規則，人或計算機只要能獲得這些產生式規則，就能解決相應的問題[12]．隨后，Anderson針對認知技能的遷移提出產生式遷移理論，其基本思想是：先后兩項技能學習產生遷移的原因是兩項技能之間產生式的重疊，重疊越多，遷移量越大[5]．信息加工心理學用產生式和產生式系統表征人的技能，技能間的遷移由共有的產生式數量決定[5]．綜上，產生式是一種規則，可以用形式化語言表征；知識可以以產生式表征，一旦獲得這些產生式就可以解決相應問題；形成一定數量且重疊的產生式越多是遷移學習的基礎．

如果準備執行一項復雜的認知操作，但對其中部分技能尚未把握或未達到自動化的程度，那么要順利地完成整個操作顯然是不可能的[5]．比如，不具備有理數運算技能，就不能解方程．因此，形成正確的產生式是執行復雜認知操作的基礎，產生式的自動化程度是順利完成復雜認知操作的基礎．同時，在執行復雜的認知操作過程中，促使各種產生式聯結與組合，形成一組產生式，這組產生式包含在當前復雜認知操作中如何行動以達到目標，便形成了一個產生式系統．

2.2 變式理論

問題變式的兩類結構：水平變式和垂直變式．水平變式是指學生能區分問題表面形式特征變化背后的結構特征變化，不帶來認知負荷的變化．垂直變式是指學生不能區分問題表面形式特征變化背后的結構特征變化，帶來認知負荷的變化．按問題結構的變化分成不同的層次（垂直變式），在同一結構層次中，可以分成問題表面形式特征不同的變化（水平變式）[13]．變式可分為等價變式和不等價變式．等價變式指變式前后的問題本質是相同的，即變化只發生在表面的形式部分[5]．

參考上述研究成果，例題變式是指圍繞核心軸（數學知識的本質結構）不變，變更例題表面的形式特征或結構特征．因此，例題變式分為3個層次．第一層次，平行變式：表面形式重復，學生認知負荷不變．第二層次，垂直變式：表面結構變化，學生認知負荷增加．第三層次，螺旋變式：圍繞核心軸，平行變式和垂直變式不斷復合，學生認知負荷加重．3個層次的變式是層層遞進的過程，平行變式是基礎，垂直變式是必然發展，二者互相依存，互相補充．螺旋變式是最高層，突出對數學結構的意義建構．

3 Q型例題的教學建議

從學習遷移的視角看，Q型例題的教學需要經歷3個階段．第一階段，形成產生式．直接利用規則，按照一定的程序，慢慢地將陳述性知識指導下的一系列操作轉化為漸漸失去陳述性意識特征的一系列操作，形成以產生式表征的程序性知識．第二階段，產生式自動化．通過平行變式和垂直變式，共有的產生式得到很好的協調和精練，協調將導致意識控制特征的逐步消失，直至達到自動化水平．第三階段，形成產生式系統．通過螺旋變式，促使各種產生式聯結與組合，形成一組產生式，構建新的產生式規則，形成一個產生式系統．下面結合案例1具體說明．

案例1：已知角的終邊經過點(2,-3)，求的正弦、余弦、正切值[14]．

3.1 形成產生式

聯系三角函數的定義，從定義的陳述性表征形式中聯結到關鍵字詞（坐標、距離和比值），執行系列操作：寫出點的橫坐標和縱坐標、計算距離、計算比值．當3個動作都被成功地執行后，相互間的聯系將會得到加強，各個動作的聯系也會更多地依靠前后動作的匹配，進而形成無意識的動作技能，即形成了以產生式表征的程序性知識．此時，陳述性意識特征將逐漸淡化．

另一方面，教師規范板書Q型例題的解答過程，其意義在于：①可視化“動作”的一步步分解演示，有利于形成正確的產生式；②規范表達的示范，是學生模仿的榜樣；③為P型例題的規范表達奠定基礎．解答過程規范表達的基本要求：①要有開始和結束的標記．如：解或證明，給出結論．②推理過程具有邏輯性和嚴謹性，不僅符合學生學習的認知序，也要順應數學發展的邏輯序．③書寫過程具有簡約性．形式上按照三段論書寫（大前提常常省略不寫），盡量運用數學符號語言表征；格式上參照古詩詞，盡量使用短句子表述，標點符號準確使用．

3.2 產生式自動化

平行變式：改變點坐標（靜態的），比如(-3, 4)，(0， 5)，等等．此時，變式問題表面形式重復，認知負荷基本保持不變．通過對表面形式特征的重復，經驗得到不斷重復．重復的意義在于始終保持了概念本質關系特征（角終邊上一點的坐標確定，三角函數值隨之確定）不變，至于“點坐標的改變”會慢慢淡化，核心是突出了不變特征．第二次的經歷豐富并加深了第一次經歷的各個方面，產生式得到重復．

垂直變式：讓點運動（動態的），比如“已知角的終邊落在直線＝3上，求的正弦、余弦、正切值”[14]．變式問題表面結構發生變化，融入策略性知識，學生認知負荷隨之增加．其表面形式變化：角的終邊落在確定直線上，點“消失”了！形式變化背后蘊含深層特征：恰恰不是點消失，而是任意多個共線點，只要選取其中一個點作為代表；另一方面，正是由于點任意多，需要分類求解，滲透策略性知識．

通過兩次變式，學生逐步擺脫陳述性知識的提示的依賴，一旦技能具有程序化的特征時，學生就不再需要停頓下來考慮下一步做什么，相反，對下一個執行動作的有意識的搜索將被自動的匹配過程所取代，即產生式達到自動化水平．

3.3 形成產生式系統

圖1 Q型例題的教學結構

4 P型例題的教學建議

P型例題具有科學的或生活的背景知識，通過數學模型的建構，意在揭示數學知識的發生過程，即對問題產生的探究．同時，通過問題解決，促進學生形成基于該數學模型的一個產生式系統．再通過例題變式，促使產生式系統得到進一步協調和發展．參考波利亞的怎樣解題表和有關研究成果[15-19]，P型例題的教學需要經歷4個階段：①弄清問題；②分析問題；③回顧反思；④變式學習．下面結合案例2具體說明．

案例2[14]：如圖2，一半徑為3 m的水輪，水輪圓心距離水面2 m，已知水輪每分鐘逆時針轉動4圈，如果當水輪上點從水中浮現時（圖中點0）開始計算時間．

（1）將點距離水面高度(m)表示為時間(s)的函數；

（2）點第一次到達最高點大約要多長時間？

4.1 弄清問題

對例題的信息進行理解，將外部信息轉化為內部信息，能用多種方式表征問題的初始狀態和目標狀態，形成問題空間．教學中，可以分3個步驟：第一步，讀一讀．讀題形式多樣：默讀、朗讀、領讀、齊讀，等等，必要時可以多讀幾遍，正如“書讀百遍其義自見”；要給學生一定的讀題時間和空間，初次讀題之前盡量不要啟發、暗示和干擾．第二步，說一說．讀到了什么？想到了什么？關鍵信息是什么？等等，引起學生思考、聯想．在學生初步理解題意時，要給學生一定的交流對話的時間和空間．特別地，生生對話是基于學生話語體系的思維碰撞，互相啟發，必要時師生對話，啟發點撥．第三步，寫一寫．關鍵信息的不同表征，如文字語言描述、畫圖標數據的圖形語言表征、引入變量的數學符號表征，必要時算一算．

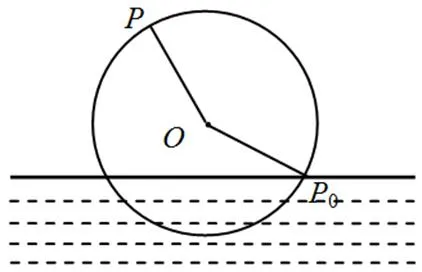
圖2 水輪運動

4.2 分析問題

分析例題的數量結構和情境結構，對外部模式進行識別，同時將外部信息與內部已有模式作比較，即模式識別過程．接著，調動與外部信息相匹配的模式，即模式的遷移．分析外部信息，識別出圓周上一點的運動，聯想到圓周運動是最簡單的周期運動，而三角函數是刻畫周期運動的基本模型．于是，匹配到三角函數模型．再根據三角函數的解析定義，自然需要引入平面直角坐標系．至于如何建立平面直角坐標系，學生是有經驗的，教學中再根據學生生成的不同坐標系進行比較、分析并加以選擇．最后，教師板書，規范表達（同上）．

4.3 回顧反思

回顧解題過程，檢驗解題過程的合理性和結果的準確性．波利亞的敘述是“檢查每一步，你能清晰地看到每一步的正確性嗎？你能證明每一步的正確性嗎？”事實上，有了詳細、明確的解題計劃，解題的過程就是按計劃落實，而落實的關鍵是保證正確．

反思解題過程，提煉解題步驟，總結解題方法，追求一題多解，發現知識能力存在的缺陷．

4.4 變式學習

第一層次：平行變式．正如蘇教版教材必修4第一章章首語所說：周期現象一般與周期運動有關，一個簡單又基本的例子便是“圓周上一點的運動”．

例如[14]：如圖3，摩天輪的半徑為40 m，點距地面的高度為50 m，摩天輪做勻速轉動，每3 min轉一圈，摩天輪上點的起始位置在最低點處．

（1）試確定在時刻(min)時點距離地面的高度；

（2）在摩天輪轉動的一圈內，有多長時間點距離地面超過70 m？

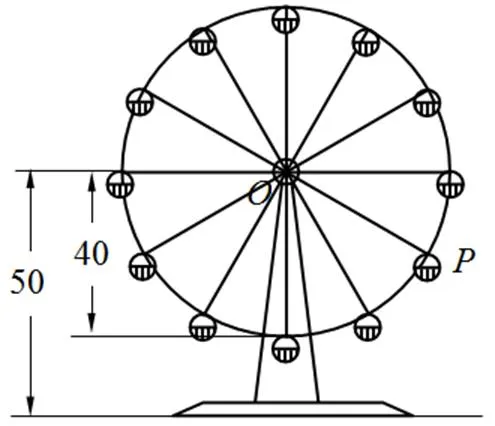
圖3 摩天輪運動

無論水輪運動，還是摩天輪運動，都在重復同一個運動：圓周上一點的運動．重復的意義在于：學生通過對表面形式特征的重復，加深并保持了深層關系特征（圓周運動是簡單且樸素的周期運動，而三角函數是刻畫周期運動的基本數學模型）．

另一方面，在問題解決過程中，基于周期模型的產生式系統中各種自動化的產生式得到重復，如：坐標系的選擇與建立，目標函數的建立，實際問題的數學表征過程（如：在摩天輪轉動的一圈內，有多長時間點距離地面超過70 m→在一個周期內使得函數值大于70時自變量的取值范圍→()＞70），不等式的求解等．重復的意義在于：各種產生式的自動化程度得到加強，促使基于周期模型的產生式系統得到精深加工．

第二層次：垂直變式．從周期背景視角，例如[14]：海水受日月的引力，在一定的時候發生漲落的現象叫潮汐，一般的早潮叫潮，晚潮叫汐．在通常情況下，船在漲潮時駛進航道，靠近船塢；卸貨后落潮時返回海洋．下面給出了某港口在某季節每天幾個時刻的水深．

時刻水深/m時刻水深/m時刻水深/m 0:005.0 9:002.518:005.0 3:007.512:005.021:002.5 6:005.015:007.524:005.0

（1）選用一個三角函數來近似描述這個港口的水深與時間的函數關系，并給出在整點時的水深的近似數值；

（2）一條貨船的吃水深度（船底與水面的距離）為4 m，該船何時能進入港口？

（3）若船的吃水深度為4 m，安全間隙為1.5 m，該船在2:00開始卸貨，吃水深度以每小時0.3 m的速度減少，那么該船在什么時間必須停止卸貨，將船駛向較深的水域？

從水輪運動→摩天輪運動→潮汐運動，變式問題表面形式特征發生變化，圓周運動“不見”了！取而代之的是一張充滿數據的表格，學生認知負荷隨之增加．這些表面變化背后不變的深層關系特征是：隨著時間的變化都有唯一的水深與之對應，具備函數關系；且自變量每增加12小時函數值（水深）不變，具有周期特征．再從表格中數據的離散性、有限性到選擇周期函數模型（三角函數）擬合數據．這就需要學生辨認當前新的情境中問題的類屬而對原有知識結構進行準確的激活，多種知識介入．

對于問題（2）、（3），厘清“吃水深度、安全間隙和吃水深度以每小時0.3 m的速度減少”的內涵，逐步數學化，實現數學符號表征；同時，能運用函數觀念統領方程、不等式．正是由于函數具備多種表現形式（解析式、列表和圖象），從而為多途徑以及尋求最佳途徑解決問題提供可能．另一方面，重疊的產生式系統得到強化，同時新問題的解決促使產生式條件的改造，能解決范圍更大的問題或更有效地解決問題．

第三層次：螺旋變式．從問題解決視角，例如[14]：煙筒彎頭是由兩個圓柱形的煙筒焊在一起做成的，現在要用矩形鐵片做成一個直角煙筒彎頭（如圖4，單位：cm），不考慮焊接處需要，選用的矩形鐵片至少應該滿足怎樣的尺寸？請你設計出一個最合理的裁剪方案．（在矩形鐵片上畫出的裁剪線應是什么圖形？）

圖4 煙筒焊接示意圖

學生面對復雜的問題情境，運用分析的方法，抽絲剝繭，逐步分解．首先，從平面圖形（矩形）到立體圖形（直角煙筒），在圖形的運動變化過程中析取變中不變的位置關系和數量關系．其次，結合數據考慮到對稱性，只需研究一個立體圖形（“圓柱形”），再將立體圖形轉化為平面圖形（截面圓），引入變量（角），進而尋求圓周上一點運動變化過程中的不變關系，得到三角函數模型．

事實上，螺旋變式以內隱的數學結構為核心，平行變式與垂直變式不斷復合，如圖5．這個變式問題的解決是一項復雜的認知操作過程，將螺旋變式問題不斷分解為平行變式和垂直變式問題，通過遷移一定數量共有的、重疊的產生式實現問題解決．同時，在問題解決過程中，學生發現蘊含其中的深層特征（三角函數概念的結構性理解和證明性理解），并能將本源的理解通過應用獲得新的理解．因此，問題解決的過程就是一種學習過程，一種創新過程，促進學生建立概念的創新性理解．如圖6是P型例題的教學結構圖．

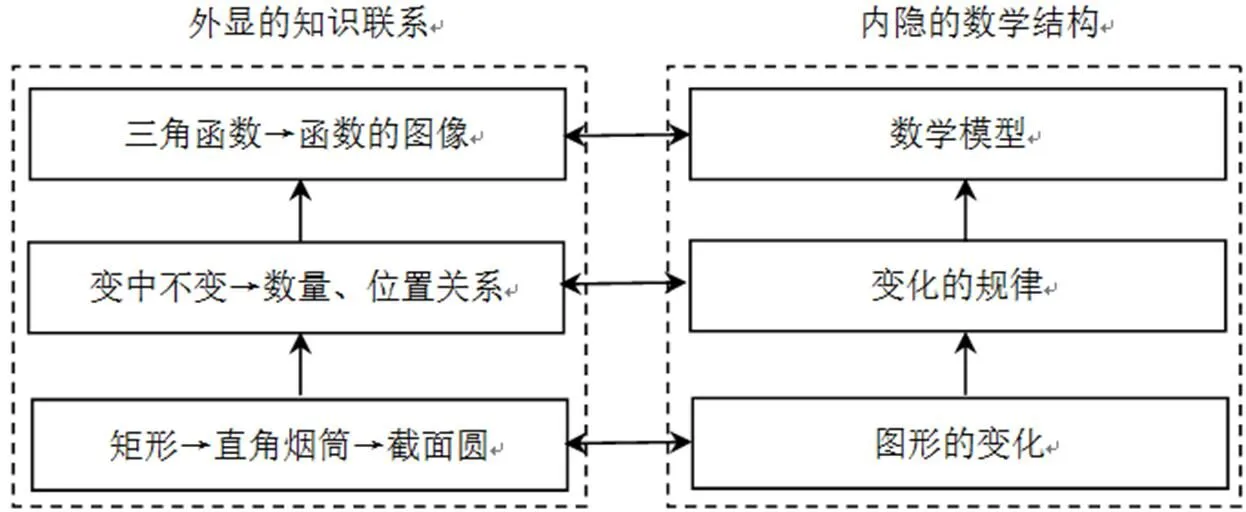
圖5 案例2的螺旋變式結構圖

圖6 P型例題的教學結構圖

[1] 王光明．數學教學效率論（理論篇）[M]．天津：新蕾出版社，2006：1-2．

[2] 李善良．論中小學數學教材編寫的基本原則[J]．數學教育學報，2007，16（1）：70-73．

[3] 王建磐，鮑建生．高中數學教材中例題的綜合難度的國際比較[J]．全球教育展望，2014，43（8）：5-9．

[4] 吳立寶，王富英，秦華．數學教科書例題功能的分析[J]．數學通報，2013，52（3）：18-23．

[5] 喻平．數學教學心理學[M]．北京：北京師范大學出版社，2010：87，101-116，304-308．

[6] 鮑建生．中英兩國初中數學期望課程綜合難度的比較[J]．全球教育展望，2002，31（9）：48-52．

[7] 胡莉莉．中美初中數學教材難度的比較研究[D]．上海：華東師范大學，2008：19．

[8] 高文君，鮑建生．中美教材習題的數學認知水平比較——以二次方程及函數為例[J]．數學教育學報，2009，18（4）：57-60．

[9] 伍春蘭．基于學生思維培養的數學定理教學的調查與分析——以“圓周角定理”教學設計為例[J]．數學教育學報，2017，26（1）：55-58．

[10] 王建波．中美澳初中數學統計課程難度的比較研究[J]．數學教育學報，2017，26（4）：50-55．

[11] 曹一鳴，吳立寶．初中數學教材難易程度的國際比較研究[J]．數學教育學報，2015，24（4）：3-7．

[12] 邵光華．樣例學習的理論與實踐[M]．杭州：浙江大學出版社，2013：51-52．

[13] 孫旭花，黃毅英，林智中，等．問題變式：結構與功能的統一[J]．課程·教材·教法，2006，26（5）：38-42．

[14] 單墫．普通高中課程標準實驗教科書·數學必修4[M]．4版．南京：江蘇鳳凰教育出版社，2012：14-46．

[15] 波利亞G．怎樣解題[M]．涂泓，馮承天，譯．7版．上海：上海科技教育出版社，2015：4-12．

[16] 寧寧，喻平．多重變異性數學樣例對遷移影響的初步研究[J]．數學教育學報，2010，19（6）：50-52．

[17] 張玲，劉靜．解代數應用題的認知模型建構[J]．數學教育學報，2017，26（1）：64-69．

[18] 陳昂，任子朝．數學高考中實踐應用能力考查研究[J]．數學教育學報，2017，26（3）：15-18．

[19] 孫旭花．中國數學教育優勢：隱性的代數教學設計模型[J]．數學教育學報，2016，25（5）：5-8．

Classification and Teaching Suggestions of Examples of Mathematics Textbooks

LU Ming-ming1, 2

(1. Xuanwu Teaching Research Office, Jiangsu Nanjing 210016, China;2. Nanjing High School Mathematics QU Dong-jian Masters Studio, Jiangsu Nanjing 210016, China)

The examples in mathematics textbooksof basic, typical, gradation, developmental, and systemic, and could be divided Q-type and P-type. The Q-type was an example of direct use of the rules and a certain procedure to complete the solution, and the function of the Q-type was to make students form the automation of skills, and the teaching of Q-type was divided into three stages: the formed production, automated production and the formed production system.The P-type example was an example of solving the problem by establishing a mathematical model, and the function of the P-type example was to acquire the strategic knowledge of problem solving, form a production system that performs complex cognitive operations; The teaching of P-type example could fall into four stages: understanding the problems, analyzing the problems, retrospective reflection and varying the learning.

example classification; example teaching; production; variations

[責任編校：周學智]

2017–12–07

江蘇省基礎教育課程教學改革重大研究項目——高中數學文化教育研究（2015jssjys-14）

陸明明（1980—），男，江蘇宿遷人，中學高級教師，主要從事數學教育研究．

G633

A

1004–9894（2018）02–0054–05

陸明明．數學教科書例題的分類及其教學建議[J]．數學教育學報，2018，27（2）：54-58．