粉末高速壓制成形件密度影響因素分析

于世偉 周 劍 張 煒 張雪潔 劉 焜

合肥工業大學摩擦學研究所，合肥，230009

0 引言

粉末高速壓制技術是在壓制壓力為600～2 000 MPa，壓制速度為2～30 m/s的條件下對粉體進行高能沖擊的壓制技術，在壓制過程中釋放的能量能夠使粉末瞬時達到致密化和均勻化［1］。目前，國內外學者主要從實驗和模擬兩方面對粉末高速壓制展開研究。WANG等［2］研究了粉末高速壓制過程中應力波的傳遞現象以及應力波對壓坯質量的影響。KHAN等［3］研究了沖擊力、沖擊速度等參數對抗拉抗彎強度以及硬度等力學性能的影響。HAGGBLAD等［4］通過改進實驗裝置的方式減少了因卸載和加載方式不當導致的密度不均和壓坯表面剝落的現象。上述文獻側重于對粉末高速壓制實驗結果的定性分析研究，對粉末密度及其均勻性量化分析較少。

YANG等［5］利用X射線斷層掃描技術，計算出粉末高速壓制獲得的壓坯自上而下7層坯料的平均密度，發現改善模具內壁潤滑條件比增大壓制壓力更能夠有效提高壓坯密度均勻性，且壓坯致密化進程通常發生在壓坯下部。TANIGUCHI等［6］先將鐵粉分次放入模具內腔進行預壓，在較大的壓力下將4層壓坯壓實，而后將4層壓坯分別分開，利用該方法研究不同潤滑劑對密度沿高度方向分布規律的影響，發現潤滑劑用量與密度均勻性的提高呈線性關系，石蠟涂抹于模具內壁時密度均勻性的改善程度要高于硬脂酸鋅涂抹于模具內壁時密度均勻性的改善程度。DOREMUS等［7］通過實驗的方式將高速壓制坯料與普通壓制坯料的密度及其分布進行了比較，發現高速壓制能夠得到密度值較大的壓坯且均勻性較好，同時發現邊壁潤滑條件對壓坯密度數值影響不大。

粉末高速壓制壓坯密度分布不均主要由顆粒間摩擦和顆粒與模具內壁摩擦引起。粉末壓制初期，顆粒處于重排階段，顆粒間摩擦起主導作用；當顆粒間壓力增大時，顆粒運動受限，顆粒與模具內壁摩擦起主導作用，且這一階段對壓坯密度的最 終分布起 決定性作 用［8］。王 德廣等［9］利用MARC軟件對粉末高速壓制進行仿真時發現，單位質量能量和高徑比等因素對壓坯密度分布有不同程度的影響。AN等［10］認為粉末初始松裝密度也對密度的分布產生影響。目前，雖然學者們研究了影響粉末高速壓制壓坯密度的各種因素，但是未進行這些因素對密度大小和均勻性的影響程度的具體定量分析。

本文利用ABAQUS中的Drucker-Prager Cap［11］本構模型，對粉末高速壓制過程進行模擬，得到粉末高速壓制壓坯相對密度分布及不同參數對密度及其均勻性的影響，并利用正交試驗手段對密度均勻性各因素的敏感性進行了分析，以期為提高粉末高速壓制成形產品的密度和均勻性提供理論指導。

1 有限元模擬

1.1 高速粉末成形過程的有限元模型建立

本文以Distaloy AE鐵粉的圓柱壓坯為研究對象，模擬研究粉末高速壓制過程中壓坯相對密度及其分布情況。該粉體的粒度分布情況如圖1所示。

圖1 Distaloy AE鐵粉粒度分布情況Fig.1 Particle size distribution of Distaloy AE

粉體壓制前尺寸由裝粉量和初始松裝相對密度決定，由于粉末壓坯和成形模具的軸對稱特征，在非線性有限元軟件ABAQUS中建立旋轉軸對稱模型，圖2為高速壓制模擬的旋轉軸對稱模型，該模型的尺寸以實際實驗中的高速壓機為參照。由于高速壓制屬于瞬態沖擊過程，因此采用ABAQUS中的顯式動力學模塊（Dynamic Explicit）進行求解，其中重錘質量為50 kg，重錘與上沖頭接觸的速度由重錘下落高度決定。下沖頭與模具之間采用完全固定的約束方式，整個沖壓過程的時間為2～4 ms，模具內腔直徑設置為16 mm，粉末體網格劃分尺寸為0.05 mm，模具網格劃分尺寸為0.2 mm。

圖2 高速粉末成形過程的有限元模型Fig.2 Finite element model of high speed powder forming process

1.2 Drucker-PragerCap材料模型及在ABAQUS中的實現

在對粉末壓制進行模擬時，選取合適的連續性材料模型是模擬粉末壓制的關鍵。Druck?er-Prager Cap（DPC）模型是在 Drucker-Prager模型的基礎上加入了蓋帽狀屈服面（CAP）［12］，它可以有效反映材料因壓縮而導致的屈服，最初用于巖土力學領域。相比于其他模型，DPC模型優點在于該模型能夠捕捉粉末中的剪切現象［13］，因而適用于粉末高速壓制的模擬。

DPC模型如圖3所示，由三段曲線組成：剪切破壞面曲線、光滑過渡面曲線和蓋帽面曲線，各曲線分別由下式定義：

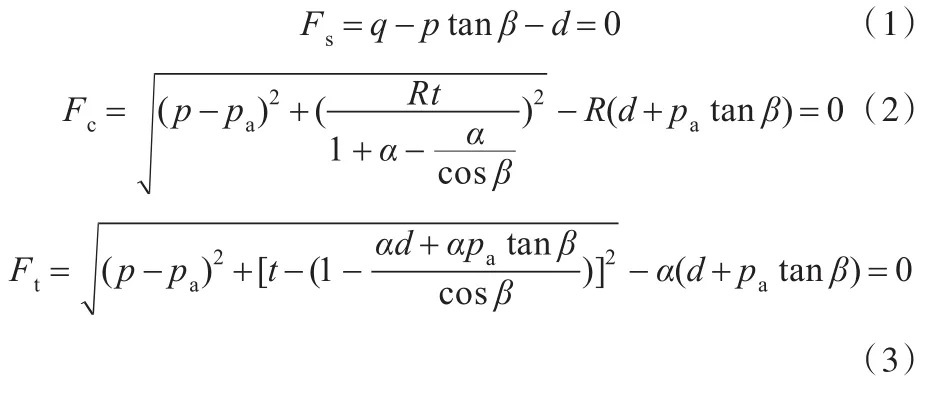
式中，p為等效壓應力；q為Misses等效應力；R為蓋帽屈服面的曲率；d為內聚力；α為過渡面曲率；β為摩擦角；pa為材料硬化的塑性體積應變參數；pb為壓縮屈服平均應力；t為偏應力。

圖3 修正DPC模型屈服面Fig.3 Yield surface of modified DPC model

Drucker-Prager Cap模型由參數d、R、β、α和k決定，k為材料參數，用于控制屈服面對中間主應力值的依賴性。由于DPC模型各參數在粉末壓制過程中隨密度（此處及下文出現的密度均指量綱一化的相對密度）不斷變化，因此ZHOU等［14］通過實驗的方法以Distaloy AE鐵粉為壓制對象，對前述參數進行擬合，以密度 ρ為自變量，各參數為因變量，其中α和K分別取0.02和1。此外在模擬中還需加入彈性模量E和泊松比υ，上述參數與密度的關系如表1所示。其中，R1和R2為常數，分別為0.23和0.58；ρc為密度擬合參數。

表1 DPC模型各參數隨密度ρ的變化公式Tab.1 The formulas of the parameters in the DPC model vary with the density in compact process

CHTOUROU等［15］在研究塑性體積應變 εV與相對密度的關系時，提出下式：

式中，ρ、ρ0分別為壓制過程中不斷變化的相對密度和壓制前的初始松裝相對密度。

本文通過有限元軟件ABAQUS提供的二次開發平臺，編寫基于Fortran語言的用戶子程序（VUSDFLD），將每一增量步所得到的各節點的體積應變數值，通過式（4）轉化成相對密度值，將相對密度定義為場變量，以不斷更新每個增量步中DPC模型各參數的值。

2 結果與討論

影響密度的參數主要為邊壁摩擦因數 μ［2］、高徑比 H/D［16］、單位質量能量 E/m［17］和初始松裝密度ρ0

［3］，其中單位質量能量為沖擊能量和裝粉量的比值。為探究在粉末高速壓制過程中不同參數對壓坯密度及均勻性的影響，本文選取上述四個參數作為自變量，密度及其均勻性作為因變量，并在模擬的過程中利用控制變量法，探究某一變量對密度及其均勻性的影響。模擬過程中，參數作為變量時的數值如表2所示。

表2 模擬過程參數變化范圍Tab.2 Parameters range in simulation process

2.1 密度分布規律

圖4為在邊壁摩擦因數為0.4、高徑比為1.5、初始松裝相對密度為0.4和單位質量能量為50 J/g條件下模擬的密度分布情況。圖4a和圖4b所示分別為壓坯整體密度分布和A、B兩點密度隨時間的變化情況。圖4a中密度分布呈現壓坯邊緣密度自上而下逐漸變小、中部密度分布較為均勻、粉末密度不均勻主要集中于靠近邊壁處的現象。這與黃培云［18］提出的密度分布規律較為吻合。圖4b中A、B兩點密度隨著時間的延長，密度差距逐漸變大，且由于回彈的作用，使得A、B兩點的密度在達到最大值后會出現較小的回落現象。

圖4c、圖4d所示分別為密度沿不同方向和區域的分布情況。從圖4c、圖4d中可以看到，上下端面的密度值隨著徑向距離的增大分別呈上升和下降趨勢；壓坯靠近邊壁的密度隨著軸向距離的增大而逐漸增大，而內部的密度沿軸向變化不明顯。這主要是由于邊壁摩擦的存在，使得應力在傳遞過程中隨傳遞距離的增大而逐漸減小，這就導致越靠近邊壁的粉末體，即壓坯邊緣處，其密度分布越不均勻，而相較之下，壓坯內部，即遠離邊壁區域，其密度分布較為均勻。

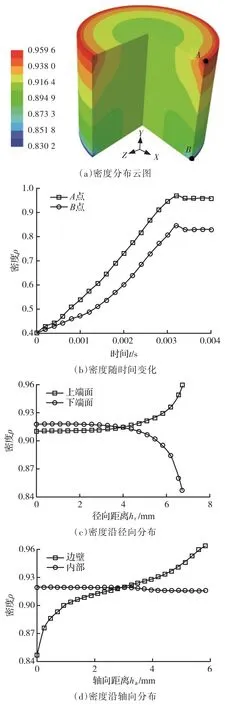
圖4 密度分布情況Fig.4 Density distribution

2.2 密度影響因素分析

圖5分別為邊壁摩擦因數 μ、高徑比H/D、單位質量能量E/m和初始松裝密度 ρ0對粉末高速壓制壓坯平均相對密度的影響。模擬結果顯示，在各影響因素中，單位質量能量對密度影響最為明顯。密度隨著單位質量能量的增大呈現先增大，后趨于不變的規律。模擬中，Distaloy AE鐵粉單位質量能量的臨界值為90 J/g，與文獻［17］中鈦粉的單位質量能量臨界值95 J/g相比較發現略小，單位質量能量的臨界值與粉末的種類有關。其他三個因素對密度的影響較小，這主要是由于這三個因素的改變并不能有效增大粉末顆粒的塑性變形，使得壓坯整體密度并不能發生較大的改變。因此在實際生產中，應從單位質量能量入手來提高壓坯密度，但一味提高高速壓制過程中的沖擊能量并不能持續提高壓坯的密度，應根據不同種類的壓制粉末選取合適的單位質量能量。

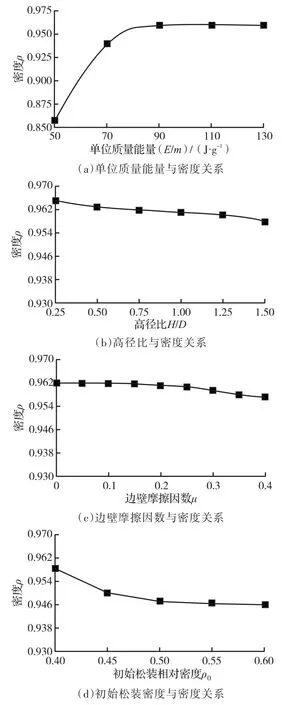
圖5 不同影響因素與密度的關系Fig.5 The relationship between different influencing factors and density

2.3 密度不均勻性影響因素分析

密度均勻性對粉末冶金制件的力學性能影響較大，因此對壓坯密度均勻性的研究具有重要意義。圖6分別為單位質量能量E/m、高徑比H/D、邊壁摩擦因數 μ和初始松裝相對密度 ρ0對粉末高速壓制壓坯密度均勻性的影響，其中密度均勻性用密度的標準差ρσ表示，標準差越小意味著密度越均勻。

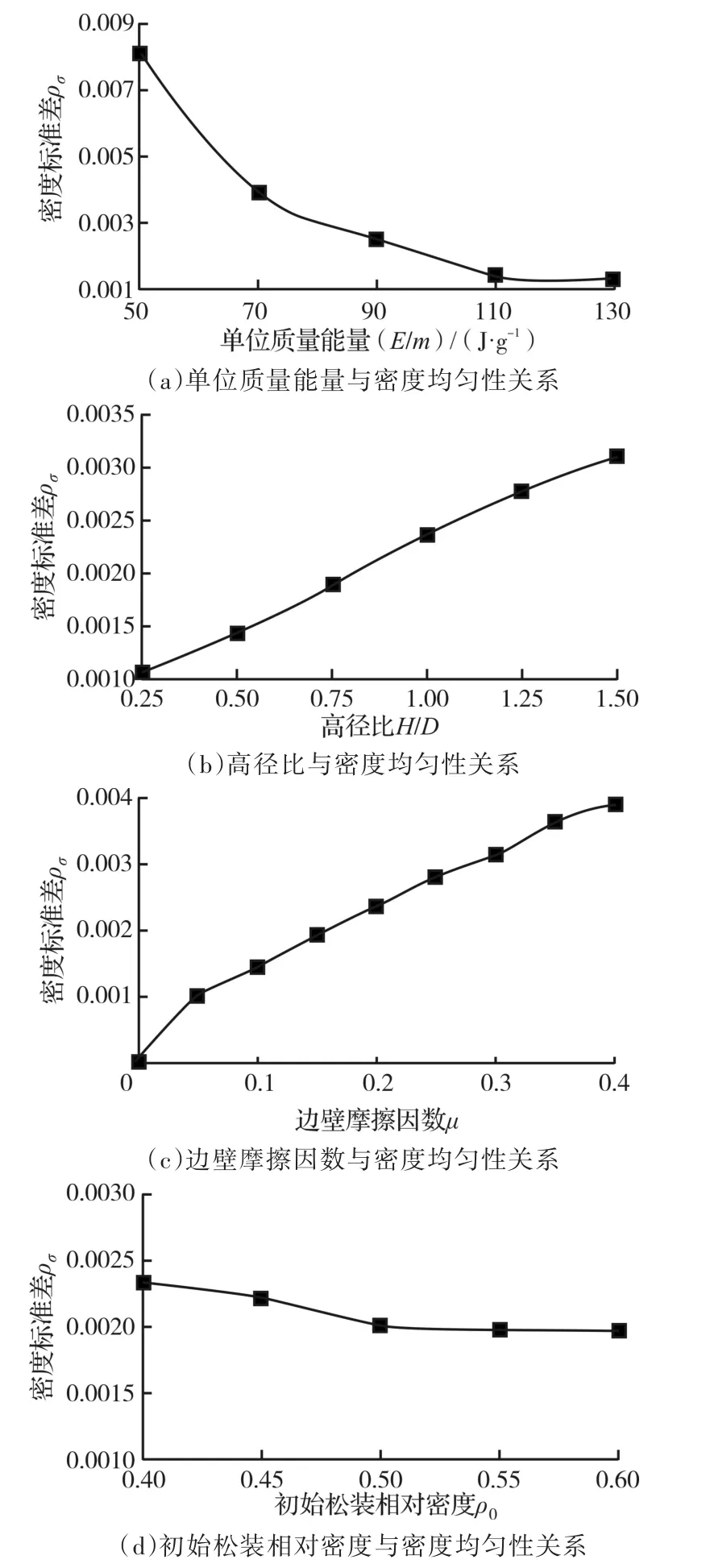
圖6 不同影響因素與密度均勻性的關系Fig.6 The relationship between different influencing factors and density uniformity

從圖6可以看出，對密度均勻性具有正相關作用的因素為單位質量能量和初始松裝相對密度；對密度均勻性具有負相關作用的因素為邊壁摩擦因數和高徑比。密度標準差隨著邊壁摩擦因數的增大而出現遞增趨勢，這主要是由于邊壁摩擦因數的增大會增大邊壁摩擦力，靠近邊壁的粉末體由于摩擦力的增大，其擠壓程度的差異變大，使得密度不均勻性加劇；同樣，高徑比和密度不均勻性也出現類似的變化規律，與邊壁摩擦因數不同的是，高徑比的增大雖然沒有增大摩擦力，但是在相同裝粉量的條件下，會增大粉末體與模具內壁接觸的側面積，從而放大了摩擦力對密度均勻性的影響；當單位質量能量增大時，密度不均勻性數值逐漸降低，當其達到110 J/g后，曲線變化趨勢趨于平緩，密度不均勻性數值趨近于一定值，結合上文中，當單位質量能量達到90 J/g時，密度不再上升，我們知道，雖然將單位質量能量從90 J/g提升到110 J/g時，密度無法進一步增大，但是其密度均勻性會進一步提高；同樣，當初始松裝密度達到0.5時，密度不均勻性數值不再下降，因此在高速壓制前，適當提高初始松裝密度至0.5左右即可達到最佳效果。

2.4 密度大小和分布不均勻性正交試驗分析

為了探究各因素對密度均勻性的影響程度，本文采用正交試驗的方式對影響程度進行定量分析。選取影響密度均勻性的主要參數為：模具內壁摩擦因數 μ、高徑比H/D、單位質量能量E/m和粉末初始松裝相對密度ρ0。根據標準正交表，選用L9（34）正交表進行試驗安排，得到結果如表3所示，其中為平均相對密度。

表3 試驗安排與結果Tab.3 Test arrangement and results

圖7為各影響因子與密度值關系圖。對密度影響的主次順序為單位質量能量、高徑比、邊壁摩擦因數和初始松裝相對密度，但是相比于單位質量能量，其余三個變量對密度值影響十分微弱，因而在實際生產中增加單位質量能量是提高密度的最有效辦法。

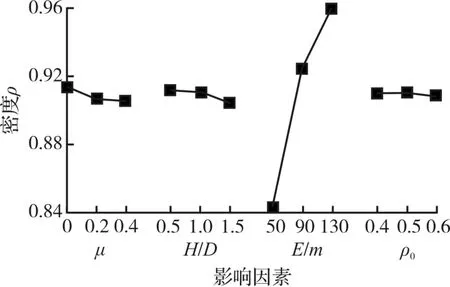
圖7 各因素對密度大小影響趨勢圖Fig.7 The tendency of density influenced by different factor

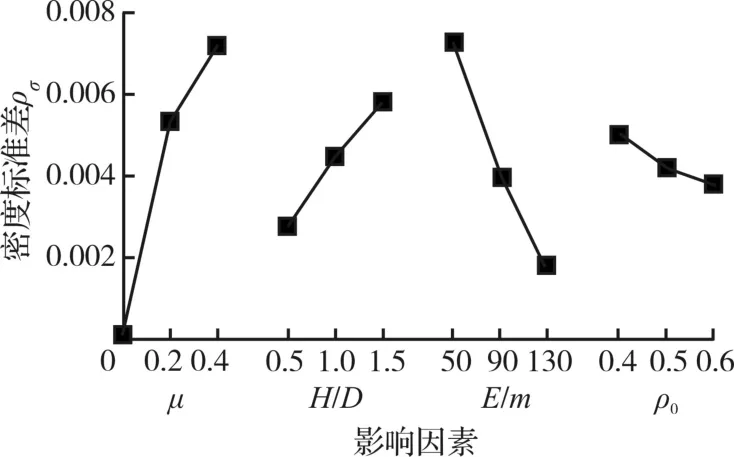
圖8 各因素對密度均勻性影響趨勢圖Fig.8 The tendency of density uniformity influenced by different factors

圖8為各影響因子與密度不均勻性關系圖，可以看到，密度均勻性隨模具內壁摩擦因數和高徑比的增大而降低，隨單位質量能量和初始松裝相對密度的增大而增大。對密度均勻性影響的主次順序為邊壁摩擦因數、單位質量能量、高徑比和初始松裝相對密度，其中最優組合為：邊壁摩擦因數為0，高徑比為0.5，單位質量能量為130 J/g，初始松裝相對密度為0.6。其中對密度均勻性影響最大的是模具內壁摩擦因數，因此改善模具內壁潤滑條件是保證粉末壓制成品密度均勻性的最為關鍵的手段之一；單位質量能量也對密度均勻性起著較大影響，隨著沖擊能量的增大，密度均勻性也在不斷改善，這也是粉末高速壓制技術優于普通壓制技術的優點之一。因此在實際生產中，應盡可能改善模具內壁潤滑條件，當潤滑條件無法進一步改善時，適當提高沖擊高度也可進一步提升密度均勻性；在某些工況下，單位質量能量和潤滑條件都無法改變時，可以通過改變粉末體的形狀因子（高徑比）和初始松裝相對密度來小幅提高密度均勻性。

3 結論

（1）壓坯密度不均勻主要集中于上下端面邊緣附近區域，其中上端面邊緣處密度最大，下端面邊緣處密度最小，邊壁摩擦的存在導致壓坯靠近邊壁處的部分密度不均勻性加劇。

（2）粉末高速壓制過程中，單位質量能量是影響密度的主要因素，提高邊壁潤滑條件、改變高徑比、提高初始松裝密度并不能有效提高壓坯密度；邊壁摩擦因數和單位質量能量對密度均勻性影響較大。

（3）密度隨著單位質量能量的增大而不斷增大，當單位質量能量達到臨界值后密度值不再增大；密度均勻性隨著邊壁摩擦因數或高徑比的增大而不斷變差，隨單位質量能量和初始松裝密的增大而不斷改善。例如，對于Distaloy AE鐵粉，單位質量能量增大到90 J/g以上時，雖然密度無法再增大，但是密度均勻性繼續改善。

參考文獻：

［1］ 周晟宇，尹海清，曲選輝.粉末冶金高速壓制技術的研究進展［J］.中國材料進展，2010，29（2）：45-49.

ZHOU Shengyu，YIN Haiqing，QU Xuanhui.Research Progress of High Speed Pressing Technology for Pow?der Metallurgy［J］.Materials China，2010，29（2）：45-49.

［2］ WANG Jianzhong，QU Xuanhui，YIN Haiqing，et al.High Velocity Compaction of Ferrous Powder［J］.Chi?nese Journal of Materials Research，2008，192（1）：131-136.

［3］ KHAN D F，YIN H Q，MATIULLAH M，et al.Analysis of Density and Mechanical Properties of Iron Powder with Upper Relaxation Assist through High Velocity Compaction［J］.Materials Science Forum，2013，749 ：41-46.

［4］ HAGGBLAD H A，HOCKAUF M，ERIKSSON M，et al.Simulation of High Velocity Compaction of Powder in a Rubber Mould with Characterization of Silicone Rubber and Titanium Powder Using a Modified Split Hopkinson Set-up［J］.Powder Technology，2005，154（1）：33-42.

［5］ YANG S D，ZHANG R J，QU X H.X-ray Tomography Analysis of Aluminum Alloy Powder Compaction［J］.Rare Metals，2015，7：1-7.

［6］ TANIGUCHI Y，DOHDA K，WANG Z.Effect of Lubri?cation on the Improvement of Uniformity in Uniaxial Powder Compaction［J］.JSME International Journal，2005，48（4）：393-398.

［7］ DOREMUS P，GUENNEC Y L，IMBAULT D，et al.High-velocity Compaction and Conventional Compac?tion of Metallic Powders：Comparison of Process Pa?rameters and Green Compact Properties［J］.Archive Proceedings of the Institution of Mecha.，2010，1（E3）：1-9.

［8］ MICHRAFY A，DODDS J A，KADIRI M S.Wall Fric?tion in the Compaction of Pharmaceutical Powders：Measurement and Effect on the Density Distribution［J］.Powder Technology，2004，148（1）：53-55.

［9］ 王德廣，吳玉程，焦明華，等.不同壓制工藝對粉末冶金制品性能影響的有限元模擬［J］.機械工程學報，2008，44（1）：205-211.

WANG Deguang，WU Yucheng，JIAO Minghua，et al.Finite Element Simulation about the Effect of Different Pressing Processes on the Performance of Powder Met?allurgy Products［J］.Chinese Journal of Mechanical Engineering，2008，44（1）：205-211.

［10］ AN Xi，ZHANG Y，ZHANG Y，et al.Finite Element Modeling on the Compaction of Copper Powder under Different Conditions［J］.Metallurgical and Materials Transactions A，2015，46（8）：3744-3752.

［11］ DRUCKER D C，GIBSON R E，HENKEL D J.Soil Mechanics and Work-hardening Theories of Plasticity［J］.Transactions American Society of Civil Engi?neers，1957，122：338-346.

［12］ BREWIN P R，COUBE O，DOREMUS P.Modelling of Powder Die Compaction［M］.London：Spring?er-Verlag，1998.

［13］ 費康，張建偉.Abaqus在巖土工程中的應用［M］.北京：中國水利水電出版社，2013：18-24.FEI Kang，ZHANG Jianwei.Application of Abaqus in Geotechnical Engineering［M］.Beijing：China Water&Power Press，2013：18-24.

［14］ ZHOU Rui，ZHANG Lianhong，BAI Yan，et al.Nu?merical Simulation of Residual Stress Field in Green PowerMetallurgyCompactsbyModified Druck?er-Prager Cap Model［J］.Transactions of Nonferrous Metals Society of China，2013，23（8）：2374-2382.

［15］ CHTOUROU H，GAKWAYA A，GUILLOT M.Model?ing of the Metal Powder Compaction Process Using the Cap Model.PartⅠ：Experimental Material Char?acterization and Validation［J］.International Journal of Solids and Structures，2002，39（4）：1059-1075.

［16］ 鄭洲順，徐丹，雷湘媛，等.粉末高速壓制成形密度分布的數值模擬及影響因素分析［J］.材料工程，2012（7）：10-14.

ZHENG Zhoushun，XU Dan，LEI Xiangyuan，et al.Numerical Simulation of Density Distribution and Analysis of Influencing Factors in Powder High Ve?locity Compaction［J］.Journal of Materials Engineer?ing，2012（7）：10-14.

［17］ 閆志巧，陳峰，蔡一湘，等.Ti粉的高速壓制成形及表征［J］.金屬學報，2010，46（2）：227-232.

YAN Zhiqiao，CHEN Feng，CAI Yixiang，et al.High Velocity Compaction and Characterization of Ti Pow?der［J］.Acta Metallurgica Sinica，2010，46（2）：227-232.

［18］ 黃培云.粉末冶金原理［M］.北京：冶金工業出版社，1997.

HUANG Peiyun.Principle of Powder Metallurgy［M］.Beijing：Metallurgical Industry Press，1997.

（編輯 王艷麗）

作者簡介：于世偉，男，1991年生，碩士研究生。研究方向為數字化設計及現代設計理論。E-mail：hfutysw@mail.hfut.edu.cn。劉 焜（通信作者），男，1963年生，教授、博士研究生導師。研究方向為先進制造技術，機電系統微觀尺寸數字化設計、表面摩擦學。發表論文180余篇。E-mail：liukun@hfut.edu.cn。