基于內含傳感器的兩電機調速系統神經網絡左逆張力辨識

劉國海　陳杰　趙文祥　袁駿　徐亮

摘 要：針對兩電機調速系統高精度張力傳感器價格昂貴、安裝要求高、材料和環境限制多的問題，提出基于“內含傳感器”的神經網絡左逆張力軟測量方法。為實現兩電機調速系統張力辨識，基于“內含傳感器”的概念，建立“內含傳感器”張力子系統，并證明其數學模型的左可逆性。考慮到逆系統模型較為復雜，存在參數時變的特點，采用BP神經網絡精確逼近張力左逆模型，并串聯在原系統之后，實現張力的辨識。基于兩電機實驗平臺，對張力辨識效果進行仿真及實驗驗證，研究結果表明，該策略能夠快速、精確地跟蹤張力實際值，且易于實現。

關鍵詞：內含傳感器；神經網絡左逆；兩電機調速系統；張力辨識

中圖分類號：TM 343

文獻標志碼：A

文章編號：1007-449X（2018）01-0023-06

0 引 言

多電機變頻調速系統具有多輸入多輸出、高階、非線性、強耦合的特點，被廣泛應用于冶金、造紙、紡織、軌道交通、印刷等現代工業領域[1-4]，這類系統需要多臺電機來傳送和抓取物料，張力的穩定是保證傳送和抓取效率的重要因素。穩定的張力不僅能夠保證物料不會因過緊而拉斷，而且能夠保證物料不因松弛而堆積。傳統的方法是通過安裝張力傳感器來實現張力的檢測和控制；但是高精度的張力傳感器價格比較昂貴，且安裝要求高，材料和環境限制因素多，嚴重限制系統的應用與推廣。所以，實現張力的軟測量是多電機協調控制領域需要解決的問題。

為此，國內外許多相關領域的學者對多電機變頻調速系統的張力辨識做了很多工作。文獻[5]和文獻[6]使用摩擦轉矩、電磁轉矩和慣性轉矩來辨識雙鼓式復卷機的張力；文獻[7]根據兩電機直流驅動系統時變偏差方程設計了張力非線性降階狀態觀測器；文獻[8]通過復卷機的卷徑、轉速、加速度和動態轉矩的全階狀態觀測器對系統張力進行辨識；文獻[9]基于紙復卷機收卷和放卷變量建立觀測模型對張力進行辨識，并通過監控當前辨識值與前一時刻參數估計值的誤差來保證張力觀測的準確性。但是，上述方法都基于系統精確的數學模型，運行過程中受到參數變化和各種內外干擾，影響辨識的準確性。

多電機變頻調速系統是一個多輸入多輸出、高階、強耦合的非線性系統，難以得到精確的數學模型，且存在模型參數變化和受到各種內外擾動的情況[10-11]，因此有必要研究不依賴系統精確數學模型的辨識策略。近年來提出的基于“內含傳感器”的左逆軟測量方法[12]可以通過函數逼近來實現不可測變量的辨識。神經網絡可以以任意精度逼近非線性函數[13-15]，本文利用基于神經網絡左逆的張力辨識策略，把神經網絡逼近任意非線性函數的特點與逆系統方法具有解耦和線性化的特點相結合，不依賴系統精確的數學模型，克服建模誤差，具有清晰直觀的物理意義。本文以兩電機變頻調速系統為例，首先證明系統的可逆性，在理論上驗證該策略的可行性。然后構建兩電機變頻調速系統模型，通過仿真對張力進行辨識。最后通過實驗驗證該策略的實際可行性。

1 基于“內含傳感器”的神經網絡左逆軟測量原理

考慮如下的非線性系統：

x·=f（x，u）。（1）

設x^=[x1，x2，…，xl]T為不直接可測變量，z=[xl+1，xl+2，…，xn]T為直接可測變量，為了實現利用直接可測變量來估計不直接可測變量，假設系統中存在一個“內含傳感器”子系統，其輸入為不直接可測變量x^，輸出為直接可測變量z，若“內含傳感器”左可逆，則可得到“內含傳感器”左逆系統，將其串聯在“內含傳感器”子系統之后得到復合系統，輸出為不直接可測變量x^，如圖1所示，即其復合系統能夠對不直接可測變量進行觀測，具有軟測量儀表的功能。

但在實際應用中，多數非線性系統都比較復雜，很難得到其精確的數學模型；而神經網絡是一種能夠對數據進行并行處理的算法，具有很強的學習和自適應能力，能夠以任意精度逼近非線性函數。因此使用神經網絡來逼近“內含傳感器”左逆系統，可以有效解決精確的數學模型無法獲取的問題。常用神經網絡有徑向基函數神經網絡（radial basis function neural network，RBFNN）和反向傳播神經網絡（back propagation neural network，BPNN）等，由于RBF網絡的訓練需要動態確定網絡結構和隱含層節點數目，考慮到實際硬件的限制，本文選擇BP網絡來逼近“內含傳感器”左逆系統，BP網絡結構如圖2所示，對于具有p維輸入q維輸出的三層BP網絡，隱含層節點數為N，其輸出為

yok=f2（∑Nj=1（f1（∑pi=1Riwij+θj）wjk+θk），k=1，2，…，q。（2）

式中f1（·）和f2（·）分別為隱含層和輸出層激活函數，每個神經元具有相應的權值w、閾值θ，權值和閾值可通過神經網絡學習算法自動調整，從而使整個神經網絡逼近目標非線性函數。

2 數學模型

考慮典型的兩電機變頻調速系統，其物理模型如圖3所示。

由于無法得到系統精確的數學模型，且存在模型參數變化以及未建模動態部分，如矢量變頻器的轉子角速度誤差，因此“內含傳感器”的左逆系統難以實現，限制了其應用。神經網絡能夠以任意精度逼近非線性函數，且不依賴系統精確的數學模型，因此將神經網絡與“內含傳感器”左逆方法相結合，可以有效解決左逆方法依賴精確數學模型的問題，并且能夠學習系統的未建模動態的規律，增強系統的抗干擾能力。神經網絡左逆軟測量模型結構如圖5所示。

4 仿真驗證

在Matlab環境中使用SFUNCTION函數構建兩電機調速系統的數學模型，分別設計轉速和張力PID控制器使系統穩定，為充分激勵出兩電機調速系統在各頻段的動靜態特性，使輸入輸出盡可能覆蓋整個工作區間，轉速給定為150～500 r/min的隨機方波，張力給定為100～600 N的隨機方波，同時采集相應的輸入輸出信號{ω1，ω2，ωr2，ω·r2，F}。張力的激勵和響應波形如圖6所示。

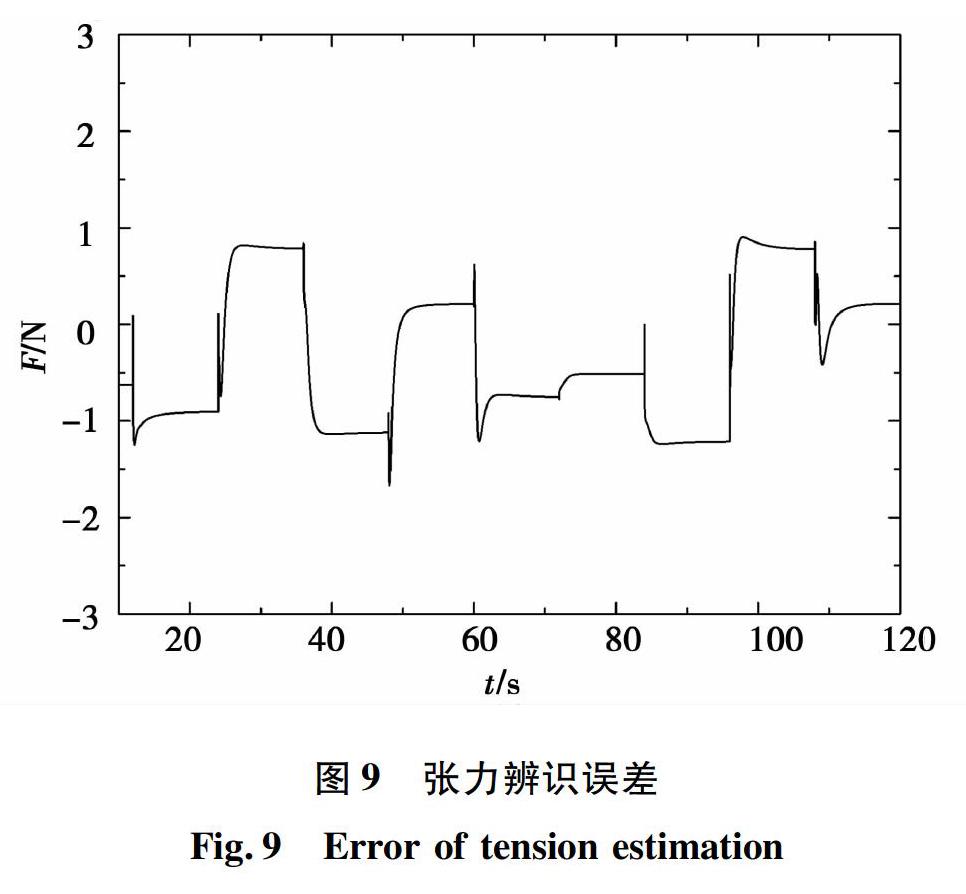
本文采用3層BP網絡，隱含層節點數為15個，對采樣數據進行掐頭去尾，使用Matlab工具箱對神經網絡進行訓練，將得到的神經網絡串聯兩電機調速系統之后，實現對張力的軟測量。神經網絡左逆張力辨識框圖如圖7所示。轉速給定為200～400 r/min隨機方波，張力給定為150～400 N隨機方波，采集兩電機調速系統實際張力與神經網絡左逆辨識的張力進行比較，如圖8所示，辨識張力與實際張力間誤差如圖9所示。

5 實驗驗證

實驗平臺包括研華上位機、西門子WinCC V6.0、西門子S7-300 PLC、數字量輸入模塊SM321、模擬量輸入模塊SM335、計數器模塊FM350、2臺2.2 kW的三相異步電機以及2臺西門子MW440變頻器。平臺及其結構如圖10所示。

實驗平臺通訊采用Profibus DP通訊協議，可在不同的兼容設備運行。實驗過程中，在PLC中編寫程序實現兩電機調速系統的PID控制算法，并通過Profibus DP控制變頻器，變頻器設置為矢量模式。為充分激勵出系統在各頻段的動靜態特性，使輸入輸出盡可能覆蓋整個工作區間，采樣過程中轉速給定為150～500 r/min的隨機方波，張力給定為120～400 N的隨機方波，WinCC通過MPI接口將{ω1，ω2，ωr2，F}從PLC采集到Excel中，Matlab調用Excel中采樣數據離線計算ωr2的一階導數，對采樣數據掐頭去尾，并使用Matlab工具箱進行訓練，訓練完成后將神經網絡權閾值導入至PLC中實現對張力的軟測量。

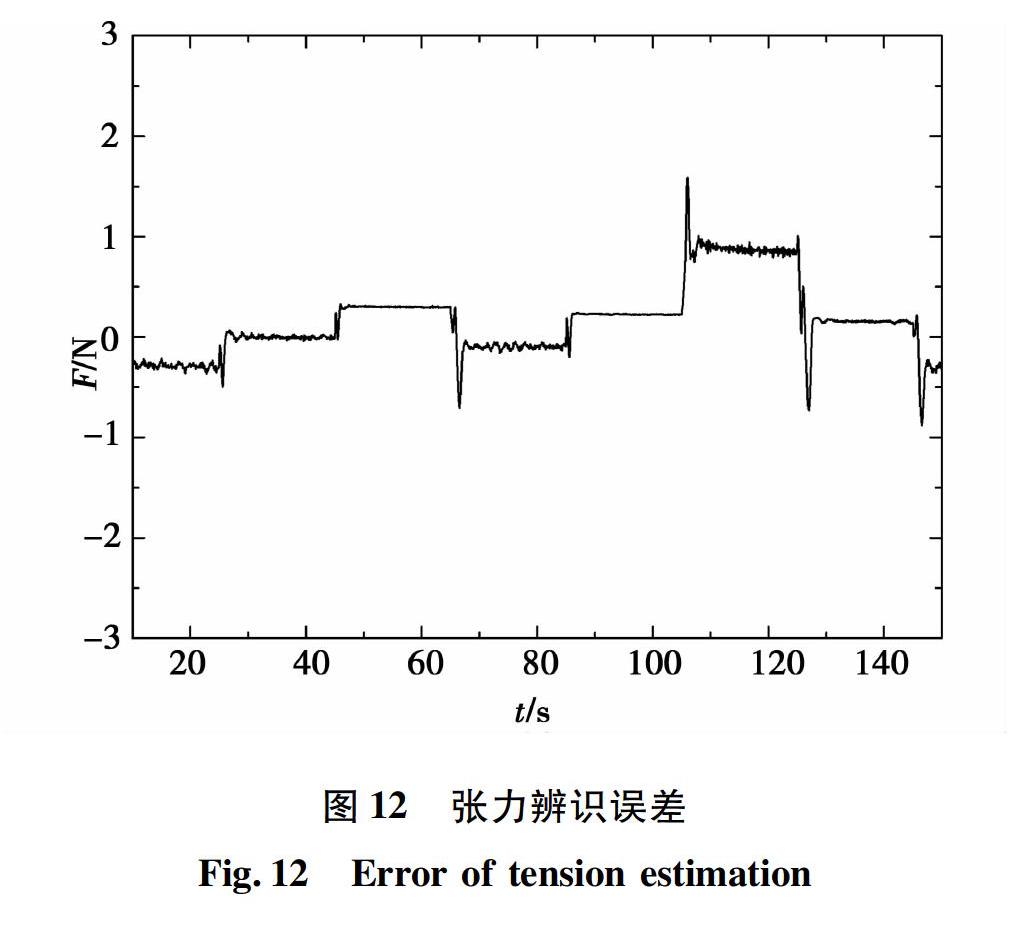
實驗中轉速給定200～400 r/min的隨機方波，張力給定150～350 N的隨機方波，采集傳感器實測張力和神經網絡左逆辨識的張力，如圖11所示，辨識張力與實際張力間誤差如圖12所示。從實驗結果可以看出，張力辨識值能夠快速跟蹤實際張力，張力最大辨識誤差在0.669%，說明本文提出的神經網絡左逆張力辨識策略可行有效。

6 結 論

本文基于“內含傳感器”的概念提出了神經網絡左逆軟測量方法。利用神經網絡不依賴系統精確數學模型以及能夠精確逼近非線性函數的特點，逼近兩電機變頻調速系統的張力“內含傳感器”子系統，實現張力的軟測量。仿真和實驗結果表明，神經網絡左逆辨識的張力能夠快速、精確地跟蹤實際值，且系統不需要添加額外的硬件，易于實現，適合張力傳感器安裝困難的場合。

參 考 文 獻：

[1] CHEESHEE LIM， LEVI E， JONES M， et al. A comparative study of synchronous current control schemes based on FCSMPC and PIPWM for a twomotor threephase drive[J]. IEEE Transactions on Industrial Electronics， 2014， 61（8）：3867.

[2] DORREL D， PARSA L， BOLDEA I. Automotiveelectric motors， generators and actuator drive systems with reduced or no permanent magnets and innovative design concepts[J]. IEEE Transactions on Industrial Electronics， 2014， 61（10）：5693.

[3] CAI Haiwei， GUAN Bo， XU Longya. Lowcost ferrite pmassisted synchronous reluctance machine for electric vehicles[J]. IEEE Transactions on Industrial Electronics， 2014， 61（10）： 5741.

[4] CAO Ruiwu， CHENG Ming，HUA Wei. Investigation and general design principle of a new series of complementary and modular linear FSPM motors[J]. IEEE Transactions on Industrial Electronics， 2013， 60（12）：5436.

[5] ABJADI N R， SOLTANI J，ASKARI J. Nonlinear slidingmode control of a multimotor webwinding system without tension sensor[J]. IET Control Theory and Applications， 2009， 3（4）：419.

[6] CARRASCO R， VALENZUELA M A. Tension control of a twodrum winder using paper tension estimation[J]. IEEE Transactions on Industry Application， 2006， 42（2）：618.

[7] LYNH A F，BORTOFF S A，ROBENACK K.Nonlinear tension observers for web machines[J].Automatica，2004，40（9）：1517.

[8] VALENZUELA M A， BENTLEY J M， LORENZ R D. Dynamic online sensing of sheet modulus of elasticity[J]. IEEE Transactions on Industry Applications， 2010， 46（1）：108.

[9] VALENZUELA M A， CARRASCO R， SBARBARO D. Robust sheet tension estimation for paper winders[J]. IEEE Transactions on Industry Applications， 2008，44（6）：1937.

[10] 劉國海，薛劍鋒，康梅，等.兩電機調速系統神經網絡廣義逆在線調整控制[J].電機與控制學報，2009，13（4）：511.

LIU Guohai， XUE Jianfeng， KANG Mei， et al. Online adjustment control of two motor speedregulating system based on neural network generalized inverse[J]. 2009，13（4）：511.

[11] 張今朝，劉國海，潘天紅.多電機同步系統的多模型辨識[J].電機與控制學報，2009，13（1）：138.

ZHANG Jinzhao， LIU Guohai， PAN Tianhong. Multimodel identification to multimotor synchronous system[J]. Electric Machines and Control， 2009， 13（1）：138.

[12] 蔣彥，劉國海，趙文祥，等.基于TDNNLI的永磁同步電機轉速辨識[J].電機與控制學報，2014，18（2）：62.

JIANG Yan， LIU Guohai， ZHAO Wenxiang， et al. Speed identification of permanent magnet synchronous motor by using TDNNLI method[J]. 2014，18（2）：62.

[13] ANDRAS P.Function approximation using combined unsupervised and supervised learning[J]. IEEE Transactions on Neural Networks and Learning Systems， 2014， 25（3）：495.

[14] 戴先中，劉國海，張興華.交流傳動神經網絡逆控制[M].北京：機械工業出版社，2007：120-134.

[15] RAZAVI S， TOLSON B A. A New formulation for feedforward neural networks[J]. IEEE Transactions on Neural Networks， 2011，22（10）：1588.

（編輯：劉琳琳）