步進電機控制系統建模及加減速曲線優化

王邦繼　劉慶想　周磊　卜朗　李相強　張健穹

摘 要：為了優化步進電機開環控制系統，對其加減速曲線的控制性能進行了研究。以步進電機運行原理為基礎，建立了兩相混合式步進電機開環控制系統仿真模型，設計了一種與電機矩頻特性更為符合且可以用于實時在線計算的拋物線型加減速曲線算法，并與典型的勻加減速曲線算法、指數型加減速曲線算法進行了仿真比較分析，最后進行了實驗驗證。仿真和實驗結果均表明，在相同的控制周期內，拋物線型加減速曲線的最大無失步轉動角度有了顯著提高，同時其中間過程的位置跟蹤誤差和平衡位置處的殘余振蕩誤差也較小。拋物線型加減速曲線具有更快速的動態響應能力，已在某相控陣列天線的單元相位控制中得到了應用。

關鍵詞：步進電機；開環控制；系統建模；加減速控制；拋物線型加減速

中圖分類號：TM 383.6

文獻標志碼：A

文章編號：1007-449X（2018）01-0037-06

0 引 言

步進電機是一種將數字脈沖轉換為相應位移增量的電磁機械。在正常工作狀態下，電機位移輸出與數字脈沖輸入嚴格同步，具有較高的控制精確度，且控制方法簡單、啟停迅速、性能穩定，廣泛應用于數控機床、機器人等領域[1]。

目前，步進電機控制方法有開環控制和閉環控制兩種。步進電機閉環控制方法見文獻[2-3]。在步進電機轉軸上安裝傳感器來檢測電機轉子位置形成閉環，并采用自適應、變結構模糊等控制算法，整個系統的實現成本和控制復雜度都較高。隨著細分驅動技術的發展，電機輸出跟蹤輸入的同步能力不斷提高，再通過合適的加減速曲線算法的優化，可以有效避免失步、振動等現象。由于其實現簡單，控制精度和系統穩定性能滿足大多數應用需求，開環控制是步進電機的主要控制方式，其研究主要集中在加減速曲線優化和具體實現上。

典型的加減速曲線有：梯形曲線、指數型曲線、S型曲線等[4-9]，它們均在一定程度上反映了矩頻特性對加速過程的限制，在適當條件下有其實用價值。周黎等人設計了一種正矢型加減速曲線[8]，能較好地抑制運動過程中的沖擊及殘余振動；但并不適合對動態響應有快速要求的場合。

本文以兩相混合式步進電機位置旋轉系統為對象，建立開環控制系統仿真模型，設計與電機矩頻特性更為符合且可用于實時在線計算的拋物線型加減速曲線算法，并與典型的加減速曲線進行仿真比較分析，最后進行實驗驗證。

2.2 矩頻特性分析

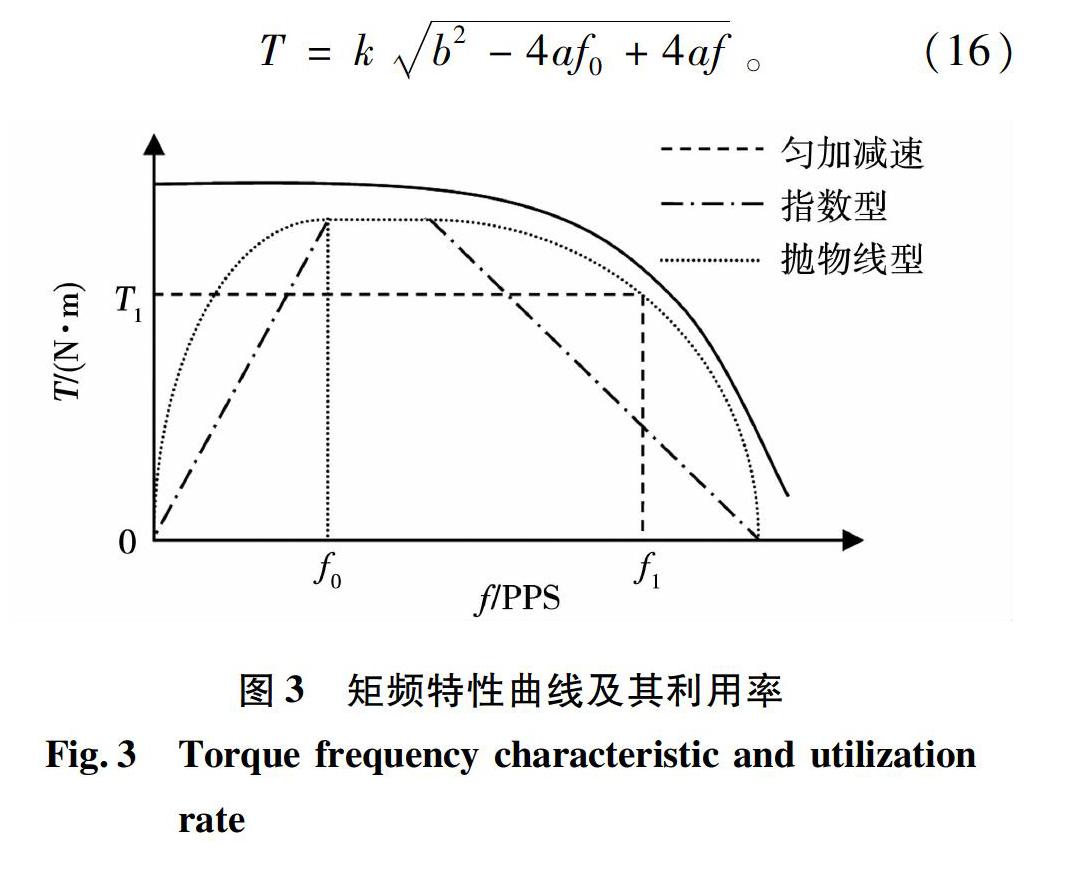
為了使步進電機既不發生失步或過沖，又能快速達到所需的運行速度，關鍵在于電機運行過程中，在各個運行頻率下所需的轉矩既能充分利用各個頻率下的轉矩，又沒有超出其轉矩。若加減速曲線在各個運行頻率下所需的轉矩完全符合矩頻特性規律，那將是一種最優的理想加減速曲線。下面分析勻加減速、指數型加減速和拋物線型加減速3種方式的矩頻特性利用情況：

1）勻加減速也稱為梯形加減速，在整個加速減過程中所需的轉矩T1是恒定的。若矩頻特性規律如圖3所示，可知該方法沒有充分利用電機低速時具有較大力矩的特點，所以加速時間與所能達到的運行頻率之間f1存在著矛盾關系。顯然這不是一種較佳的加速方式。

2）指數型加減速，其加速度與運行頻率之間滿足的線性變化規律[8]為

dfdt=A-Bt。（15）

通常的步進電機矩頻規律為：在運行頻率f較小時，電機轉矩T基本恒定，而當f增大時T隨f近似線性下降，所以，式（15）是對電機矩頻特性的一種較好的近似。

3）拋物線型加減速。通常的步進電機矩頻規律為：在f0后的一段內，T隨f線性下降，但斜率不大；而當f較大時，T隨f的下降加快。對于這種矩頻特性，拋物線型加減速曲線能更好地符合其矩頻特性規律，這是因為拋物線型加減速曲線所需的轉矩與運行頻率的關系[12]為

3 仿真分析

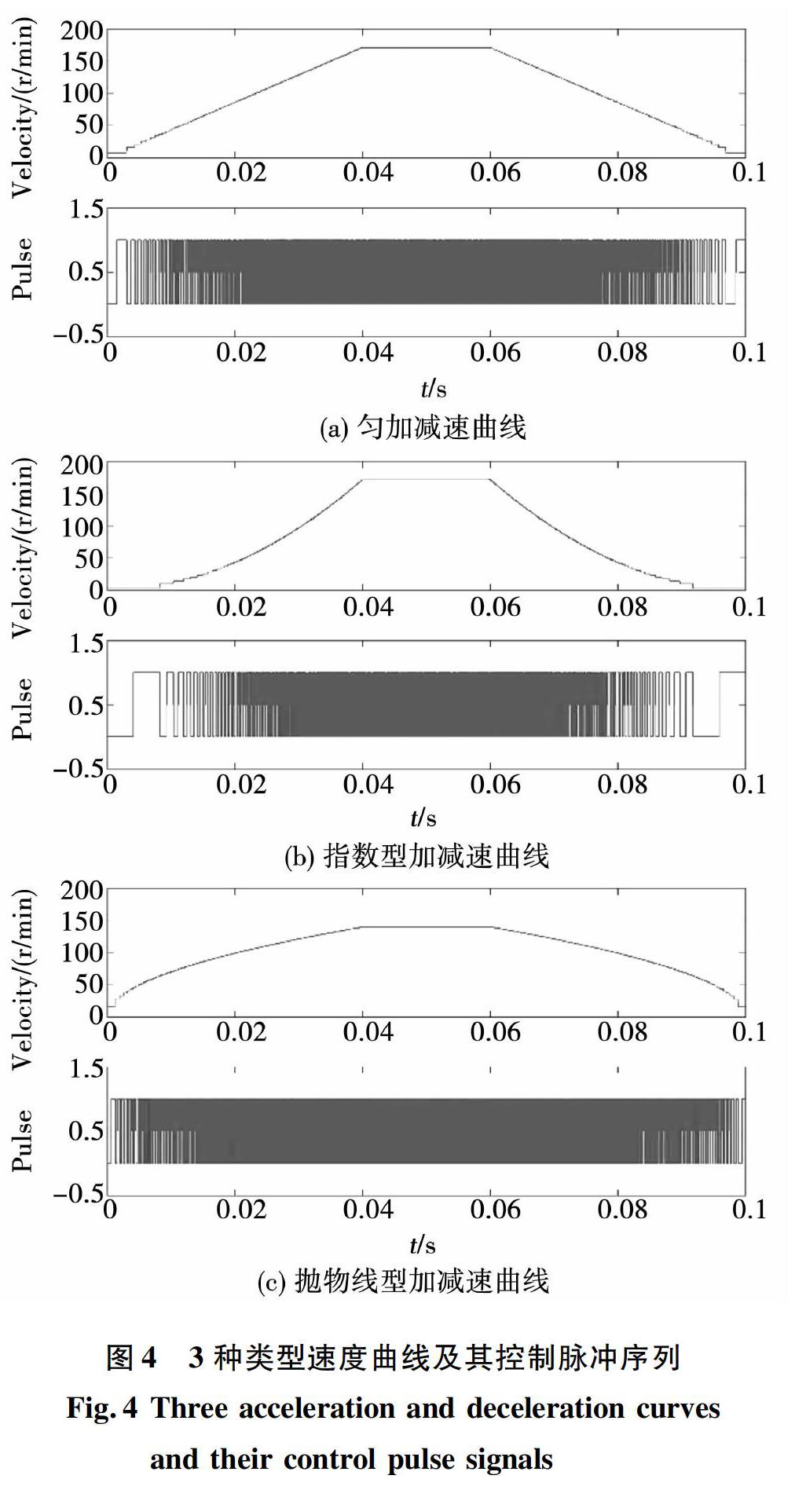
以某步進電機位置旋轉系統為對象，利用前文的步進電機開環控制系統仿真模型，對上述3種加減速曲線分別進行仿真研究。采用SanyoDenki公司生產的邊長為14 mm的兩相混合式步進電機，轉子齒數為50齒，最大輸出轉矩為6.5 mN·m。采用256細分的微步細分驅動，理論上的步進角達到了0.007°。負載轉動慣量JL取3×10-7 kg·m2，電機軸轉動慣量JM為0.58×10-7 kg·m2，粘滯阻尼D取0.0001 N·m·s/rad。電機從靜止啟動到剛好停止的轉動時間為100 ms，其中加速、勻速和減速時間分別為40 ms、20 ms和40 ms。這3種加減速方式下設計的速度曲線及其相應的步進脈沖序列的典型仿真結果如圖4所示。

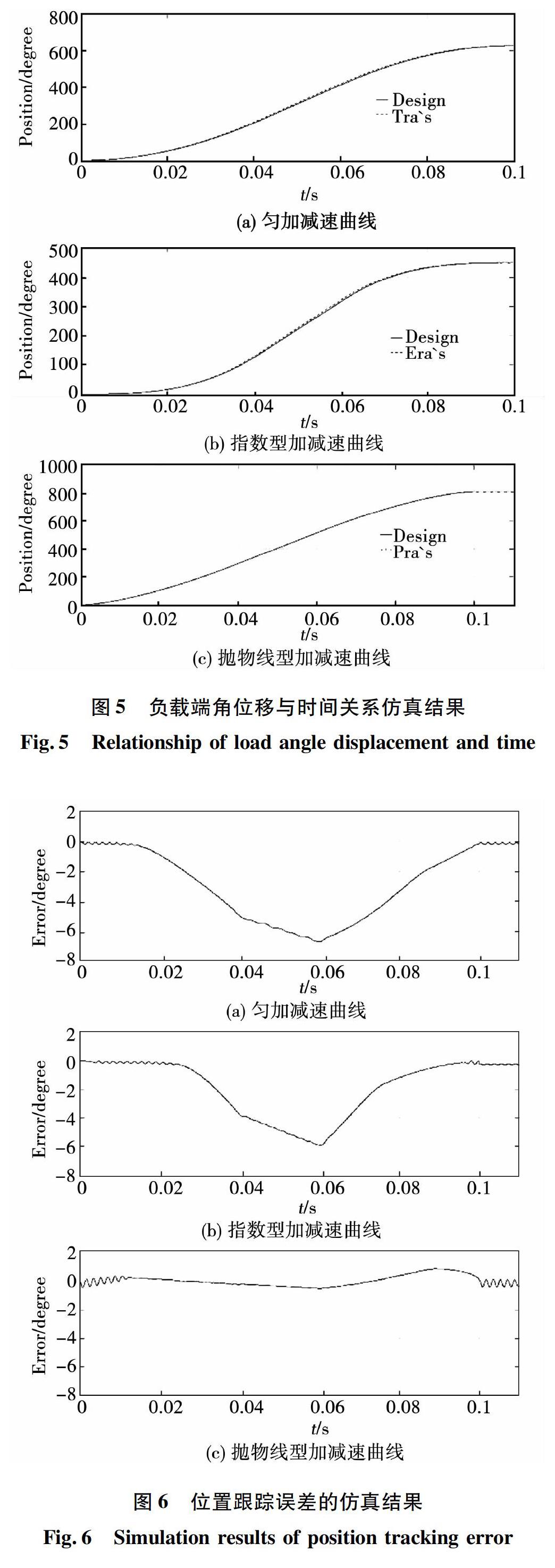
分別采用這3種速度曲線作為仿真系統輸入，執行仿真系統，可以得到負載運動的速度、位置曲線等。仿真結果表明：在100 ms控制周期內，采用勻加減速曲線，步進電機的最大無失步轉動角度為630°；采用指數型加減速曲線，最大無失步轉動角度為450°，較勻加減速曲線降低了180°；而采用拋物線型加減速曲線，最大無失步轉動角度達到810°，較勻加減速曲線提高了180°，提高了約30%。在最大無失步轉動過程中，這3種速度曲線的負載端角位移與時間關系仿真結果如圖5所示，其中實線為輸入的角位移曲線（設計的速度曲線的一次積分），虛線為負載端的角位移曲線。可以看出，這兩種角位移曲線具有較好的吻合程度，說明設計的速度曲線能夠實現對步進電機的精確控制。將它們作差值處理，將得到運行過程中的位置跟蹤誤差，以及輸入停止后負載在平衡位置處的殘余振蕩過程，如圖6所示。可以看出，拋物線型加減速曲線的中間過程位置跟蹤誤差最小，而在平衡位置處的殘余振蕩誤差也較小，在-0.5° ～ 0.5°范圍內。在上述電機轉動過程中，這3種加減速方式下設計的速度曲線與仿真得到的負載端的速度曲線與時間關系如圖7所示。這3種加減速的速度曲線均基本符合預期的設計要求，但在速度曲線不同階段的轉換處所需轉矩不平滑，有一定的諧振振蕩沖擊，可能會誘發系統機械振動。

綜上所述，拋物線型加減速曲線在相同控制周期內具有更大的轉動角度，即具有更快的動態響應速度，同時中間過程的位置跟蹤誤差也較小，這說明拋物線型加減速曲線具有更優的開環控制特性。

4 實驗驗證

前述的梯形速度曲線和拋物線型速度曲線已在Altera公司的DE0 FPGA開發板上得以實現。驅動對象的參數與仿真模型基本吻合，即采用靜轉矩為6.5 mN·m、額定電流為0.3 A、電機軸轉動慣量為0.58×10-7 kg·m2、編碼器線數為1024的兩相混合式步進電機。旋轉負載的轉動慣量約為3×10-7 kg·m2，驅動電路的微步細分數為16。加速、勻速和減速時間分別為40 ms、20 ms和40 ms，即單個控制周期的總運行時間精確為100 ms。

梯形和拋物線型速度曲線的最大無失步轉動角位移及其相應的誤差曲線如圖8和9所示。可以看出，在100 ms的控制周期內，梯形加減速方式的最大無失步轉動角度為540°；而拋物線型加減速方式的最大無失步轉動角度為810°，較梯形加減速方式有了約50%的提高。同時，在系統停止輸入后，負載在平衡位置處的殘余振蕩誤差也均在-0.5° ～ 0.5°的范圍內。

在其他轉動角度下也進行了實驗測試，這兩種速度曲線在不同轉動角度下的中間過程角位移誤差最大值總結于表1中。在相同的控制周期內，較梯形曲線來說，拋物線型曲線具有更大的無失步轉動角度，同時中間過程角位移誤差也有所降低。實驗與仿真結果及其規律基本吻合，證明了前述矩頻特性理論分析的正確性。拋物線型加減速方式的運用，使步進電機的開環控制性能有了顯著提高。

5 結 論

1）建立了兩相混合式步進電機開環控制系統仿真模型，設計了一種與步進電機矩頻特性更為符合且可以用于實時在線計算的拋物線型加減速曲線算法。

2）仿真分析了勻加減速、指數型加減速、拋物線型加減速3種類型速度曲線的控制性能。結果表明，在100 ms的控制周期內，拋物線型加減速曲線的最大無失步轉動角度達到810°，較另外兩種加減速曲線分別提高了29%和80%；同時其中間過程的位置跟蹤誤差和平衡位置處的殘余震蕩誤差均較小。

3）實驗研究了梯形、拋物線型速度曲線的控制性能。結果表明，在相同控制周期下，拋物線型速度曲線的最大無失步轉動角度為810°，較梯形速度曲線有了約50%的提高；同時其角位移誤差也相對減小。仿真和實驗都說明了拋物線型加減速曲線具有更快速的動態響應能力。

4）基于拋物線型加減速曲線的步進電機開環控制方式已成功應用到某相控陣列天線的單元相位控制中，實現了天線波束更快速的動態掃描性能。該控制方式也適用于對響應速度有較高要求的其他應用場合。

參 考 文 獻：

[1] ACARNLEY P. Stepping Motors： A guide to theory and practice[M]. London： The Institution of Electrical Engineers， 2002.

[2] 史敬灼， 徐殿國， 王宗培. 模糊控制步進電動機位置伺服系統[J]. 電工技術學報， 2001， 16（3）：20.

SHI Jingzhuo， XU Dianguo， WANG Zongpei. Stepping motor position servo system with fuzzy control[J]. Transactions of China Electrotechnical Society， 2001，16（3）：20.

[3] 劉景林， 王帥夫. 數控機床用多步進電機伺服系統控制[J]. 電機與控制學報， 2013， 17（5）：80.

LIU Jinglin， WANG Shuaifu. Multistepping motor servo system control for numerical control machine[J]. Electric Machines and Control， 2013， 17（5）：80.

[4] 劉穎， 王志剛， 王紅， 等. 步進電機升降頻的優化算法[J]. 微電機， 2010， 43（8）：93.

LIU Ying， WANG Zhigang， WANG Hong， et al. An optimization algorithm to accelerate or decelerate speed of step motor[J]. Micromotors， 20010， 43（8）：93.

[5] 王邦繼， 劉慶想， 周磊， 等. FPGA在多軸步進電機控制器中的應用[J]. 電機與控制學報， 2012，16（3）：78.

WANG Bangji， LIU Qingxiang， ZHOU Lei， et al. FPGAbased multipleaxis stepper motor controller[J]. Electric Machines and Control， 2012， 16（3）：78.

[6] CARRICA D O， GONZALEZ S A， BENEDETTI M. A high speed velocity control algorithm of multiple stepper motors[J]. Mechatronics， 2004， 14：675.

[7] JI Shuai， HU Tianliang， ZHANG Chengrui， et al. A parametric hardware fine acceleration/deceleration algorithm and its implementation[J]. Int J Adv Manuf Technol， 2012， 63：1109.

[8] 周黎， 楊世洪， 高曉東. 步進電機控制系統建模及運行曲線仿真[J]. 電機與控制學報， 2011， 15（1）： 20.

ZHOU Li， YANG Shihong， GAO Xiaodong. Modeling of stepper motor control system and running curve simulation[J]. Electric Machines and Control， 2011，15（1）：20.

[9] 巫佩軍， 楊文韜， 余馳， 等. 一種用于高精度隨動控制系統的軌跡預測方法[J]. 電機與控制學報， 2014， 18（7）：1.

WU Peijun， YANG Wentao， YU Chi， et al. Trajectory prediction method for high precision servo control system[J]. Electric Machines and Control， 2014， 18（7）：1.

[10] 劉衛國， 宋受俊. 三相反應式步進電動機建模及常用控制方法仿真[J]. 微電機， 2007，40（8）：22.

LIU Weiguo， SONG Shoujun. Modeling and simulation of conventional control methods for 3phase reluctance stepper[J]. Micromotors， 2007， 40（8）：22.

[11] LYSHEVSKI S E. Microstepping and high performance control of permanentmagnet stepper motors[J]. Energy Conversion and Management， 85（2014）：254.

[12] 陳愛民. 步進電機拋物線型升降頻曲線介紹[J]. 微特電機， 1991，6：42.

（編輯：張 楠）