極限狀態法在游樂設施結構設計上的應用

鄧貴德 沈功田 張 勇 宋偉科 徐永生

（中國特種設備檢測研究院 北京 100029）

目前，我國游樂設施的基礎設計標準為GB 8408—2008 《游樂設施安全規范》。該標準規定游樂設施結構的設計計算應包括應力計算、剛度計算、疲勞強度計算、穩定性計算、抗傾覆計算、防側滑計算等，其中應力計算采用單一安全系數的許用應力設計法，要求游樂設施零部件及焊縫承受的最大應力不超過材料抗拉強度與許用安全系數之比，對于重要的軸、銷軸及重要焊縫，許用安全系數≥5；對于一般構件，許用安全系數≥3.5（脆性材料≥8）[1]。

上述許用安全系數不但較大于歐盟和美國游樂設施標準中規定的安全系數，也大于起重機械、壓力容器等特種設備規范標準規定的對應安全系數。因此，我國目前的游樂設施普遍存在結構設計笨重的問題，這一方面直接增加了承載結構的材料消耗和自重，另一方面運動構件自重增大會導致游樂設施電機、傳動、制動等系統的成本大大增加，并加大了游樂設施運行過程中的能源消耗和運營成本。

極限狀態法是一種以概率理論為基礎、以分項系數表達、不使結構超越某種規定極限狀態的設計方法，在建筑、鐵路、公路、港口、水利水電等工程結構設計方面逐漸取代了傳統的許用應力設計法，近年來也陸續被歐盟、美國、澳大利亞等國外游樂設施標準采納。本文介紹了極限狀態法的基本概念和應用現狀，并對2個國外主要游樂設施設計標準EN 13814：2004和ASTM F2291—17中采納的極限狀態法進行了分析和比較，著重對比了極限狀態、載荷組合、抗力系數等內容，在此基礎上提出了在中國游樂設施標準中引入極限狀態設計法的建議，并指出了需要進一步開展研究的內容。

1 極限狀態設計法

1.1 極限狀態

根據ISO 2394：2015《結構可靠性通用準則》[2]、GB 50153—2008 《工程結構可靠性設計統一標準》[3]等標準，極限狀態是指整個結構或者結構構件進入的某種特定狀態，超過該狀態后整個結構或結構構件就不再滿足設計規定的某一功能要求。簡而言之，極限狀態就是區分結構或構件失效與否的臨界狀態。

結構極限狀態分為承載能力極限狀態和正常使用極限狀態。承載能力極限狀態對應于結構或構件達到最大承載力或進入不適于繼續承載的變形狀態，當結構或構件出現如下狀態之一時，應認為超過了承載能力極限狀態[3]：

1）結構構件或連接因超過材料強度而破壞，或因過度變形而不適于繼續承載；

2）整個結構或其一部分作為剛體失去平衡；

3）結構轉變為機動體系；

4）結構或其構件喪失穩定；

5）結構因局部破壞而發生連續倒塌；

6）地基喪失承載力而破壞；

7）結構或構件疲勞破壞。

正常使用極限狀態對應于結構或構件達到正常使用或耐久性能的某項規定限值的狀態，當結構或構件出現如下狀態之一時，應認為超過了正常使用極限狀態[3]：

1）影響正常使用或外觀的變形；

2）影響正常使用或耐久性能的局部損傷；

3）影響正常使用的振動；

4）影響正常使用的其他特定狀態。

結構設計時應對結構的不同極限狀態分別進行計算，當某一極限狀態的計算起控制作用時，可僅對該極限狀態進行計算。

1.2 設計計算原理

結構的極限狀態可用如下極限狀態方程描述[3]：

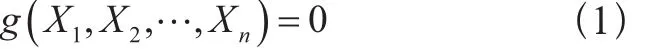
式中：

g(·)——結構的功能函數；

——基本變量，指作用在結構上的各種載荷和環境影響、材料性能參數、幾何尺寸參數等。

結構按極限狀態設計時應符合下式要求：

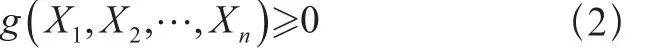
當采用結構的載荷效應和結構的抗力作為綜合基本變量時，結構按照極限狀態設計應符合下列要求：

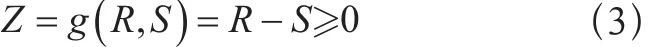
式中：

R——結構的抗力，即結構承受載荷效應的能力；

S——載荷或載荷組合在結構中產生的效應，廣義的載荷效應包括結構應力、應變、撓度、轉角、內力、力矩或者其他極限狀態控制值，狹義的載荷效應可以選定為應力。

結構抗力通常是所用材料力學性能和結構幾何參數的函數，載荷效應則與結構可能承受的各種載荷特性有關。R和S都是與基本變量相關的隨機變量，因此Z也是一個隨機變量，隨機變量Z以某一概率的形式滿足式（3）的要求，這個概率值就是結構的可靠度，與之相對的則是結構的失效概率。

1.3 結構可靠度與失效概率

結構可靠度是度量結構可靠度的指標，定義為結構在規定的時間內和規定的條件下，完成預定功能的概率。與之相對，失效概率則是指結構不能完成預定功能的概率。

失效概率Pf表達式如下：

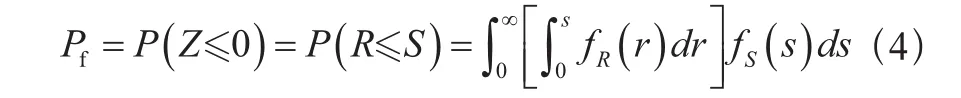
式中：

fR(r)——結構抗力的概率密度函數；

fS(s)——載荷效應的概率密度函數。

根據失效概率Pf，可以計算結構可靠度Pre：

除了結構可靠度Pre外，可靠指標β也常用于衡量結構的可靠性，可靠指標與可靠度和失效概率的關系如下：

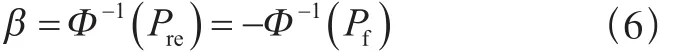
式中：

Φ?1(·)——標準正態分布函數的反函數。

當抗力R和載荷效應S都為服從正態分布的隨機變量且相互獨立時，可靠指標β有如下表達式[4]：

式中：

μR、μS——結構抗力和載荷效應的平均值；

σR、σS——結構抗力和載荷效應的標準差。

1.4 載荷組合

載荷按照隨時間的變化，可以分為永久載荷、可變載荷和偶然載荷。永久載荷如結構自重，隨時間變化很小，通常可按照隨機變量進行統計分析。可變載荷如風載荷、雪載荷和乘員活載荷等，載荷隨時間變化量大，屬于隨機過程，但是考慮到隨機過程處理復雜，通常采用簡化的隨機過程概率模型描述，即將設計基準期內載荷的標準值作為隨機變量代替隨機過程來進行統計分析。偶然載荷如地震載荷、爆炸載荷等，在結構設計使用年限內不一定出現，一旦出現其量值很大但持續時間很短。偶然載荷按照可能出現的最大值確定設計值，如地震載荷可按照地震載荷的重現期確定設計值[3]。

當結構承受兩種或兩種以上的可變載荷作用時或者可變載荷和偶然載荷作用時，考慮到這些載荷同時出現最大值的概率很小，通常可以對起主導作用外的伴隨可變載荷乘以小于1的組合系數，折減后進行載荷組合。

在進行承載能力極限狀態設計時，通常需要考慮基本組合和偶然組合兩種載荷組合工況，其中基本組合適用于結構使用過程中一定出現且持續期很長的設計狀況，以及施工和使用過程中出現概率較大但持續期很短的設計狀況；偶然組合適用于結構使用過程中出現概率很小且持續期很短的設計工況，兩種載荷組合形式見式（8）和式（9)；在進行正常使用極限狀態設計時，可根據不同情況采用載荷的標準組合、頻遇組合或準永久組合，組合形式分別見式（10）～式（12)[3]。

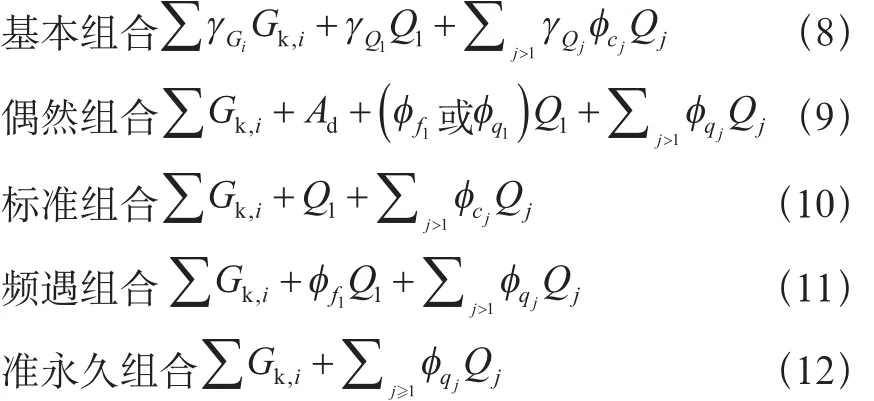
式中：

Ad——偶然載荷的設計值；

Gk,i——第i個永久載荷標準值；

Q1——第1個可變載荷（主導可變載荷）標準值；

Qj——第j個可變載荷標準值；

γGi——永久載荷分項系數；

γQ1——第1個可變載荷分項系數；

γQj——第j個可變載荷分項系數；

φcj——第j個可變載荷的組合值系數；

φf1——第1個可變載荷的頻遇值系數；

φq1——第1個可變載荷的準永久值系數；

φqj——第j個可變載荷的準永久值系數。

需要指出的是，上述載荷組合表達式中符號“∑”和“+”均表示組合，即同時考慮所有載荷對結構的共同影響，而不表示代數相加。

1.5 分項系數

極限狀態法被認為是一種先進的結構設計方法，但是直接采用1.3節介紹的可靠度方法進行結構設計需要概率和數理統計學基礎且涉及概率運算，對于大多數設計人員來說應用存在困難。為此，國內外研究人員通過人為引入分離函數的方式將可靠指標分解換算，表達成設計人員習慣采用的分項安全系數，使極限狀態設計法與傳統單安全系數設計方法形式相近，這樣既內含了結構可靠性設計基本要求，又不直接涉及統計參數、概率模型和概率計算，便于工程實際應用。

式（13）是一種典型的采用分項系數表示的承載能力極限狀態設計表達式[3]：

式中：

Rd——抗力設計值；

Sd——載荷組合效應值；

γ0——結構的重要性系數；

γM——抗力分項系數；

σM——材料力學性能標準值。

式（13）中包含的抗力分項系數γM，以及式（8）～式（12）中的載荷分項系數γGi、γQ1、γQj、φcj、φf1、φq1和φqj，由標準規范的研制人員根據結構承受載荷、所用材料以及幾何尺寸等各變量的概率模型、統計特性，在規定的失效概率或者目標可靠指標條件下，按照結構可靠度方法針對有代表性的典型結構計算分析得到。如果未給出具體的目標可靠度，則宜用校準法對按傳統許用應力法設計的已有結構進行反演計算，求得已有結構可靠指標，并經綜合分析判斷決定。

1.6 應用現狀

目前，歐盟境內所有的建筑和土木工程結構設計均采用基于《歐洲結構規范》的極限狀態設計法，以消除妨礙歐盟成員國市場自由的技術壁壘，并確保歐盟境內的工程結構具有一致的安全可靠性[5]。歐洲起重機械標準規定的首選設計校核方法為極限狀態法，但是對于載荷和載荷效應成線性關系的MDC1級起重機械可以采用許用應力法[6]。美國公路橋梁設計規范從20世紀80年代后期引入了基于結構可靠性和極限狀態設計理論的載荷抗力系數法（LRFD），1994年至2006年與許用應力法并行使用，2007年后完全采用極限狀態法設計規范[7]。

目前，我國房屋建筑、鐵路、公路、港口、水利水電等工程結構設計均已引入極限狀態設計方法。為了統一這些工程結構設計的基本原則、要求和方法，我國制定頒布了《工程結構可靠性設計統一標準》，規定工程結構設計宜采用以概率理論為基礎、以分項系數表達的極限狀態設計方法，當缺乏統計資料時也可采用容許應力或單一安全系數等經驗方法[3]。我國的《起重機設計規范》規定起重機結構設計計算可采用許用應力設計法或極限狀態設計法，當結構在外載荷作用下產生了較大變形，以致內力與載荷呈非線性關系時，宜采用極限狀態設計法[8]。

2 歐美游樂設施設計標準比較

EN 13814：2004 《游樂場所機械和結構安全》[9]、ASTM F2291—17 《游藝機和游樂設施設計標準慣例》[10]是歐盟和美國現行最新的游樂設施設計標準。這兩個標準均引入了極限狀態設計方法用于游樂設施結構設計，其中EN 13814：2004只規定了極限狀態設計法，ASTM F2291—17規定可以采用許用應力法或載荷抗力系數法，其中載荷抗力系數法實質就是一種以分項系數表達的極限狀態設計法。

2.1 針對的極限狀態

EN 13814: 2004在第5.1.4條明確規定，設計驗算應當包括承載能力極限狀態，疲勞極限狀態，屈曲極限狀態，變形極限狀態（必要時），抗傾覆、抗滑移和抗提升安全驗證以及動態分析。參照GB 50153—2008對于承載能力極限狀態的規定，疲勞、屈曲、抗傾覆、抗滑移和抗提升以及過度變形均屬于承載能力極限狀態，因此可以進一步歸納認為，EN 13814：2004針對的極限狀態主要是承載能力極限狀態，以防止結構出現靜強度失效、疲勞失效、穩定性失效、過度變形等失效模式。

ASTM F2291—17的設計部分規定，設計人員應當分析校核結構不會出現顯著塑性變形或者垮塌，應當采用強度和疲勞兩個準則來評價應力結果；對于移動式游樂設施，還規定要確保其不會發生傾覆；如果結構部件或者結構整體變形對結構正常運行有影響時，還應當進行變形分析。同樣，參照GB 50153—2008的規定，ASTM F2291—17針對的極限狀態有承載能力極限狀態和正常使用極限狀態，承載能力極限狀態校驗主要是防止靜強度失效、疲勞失效、穩定性失效等失效模式，正常使用極限狀態是防止出現影響正常工作的變形。

2.2 規定的載荷組合

●2.2.1 EN 13814: 2004

EN 13814: 2004第5章要求游樂設施承載結構極限狀態應當考慮基本組合、偶然組合和疲勞組合三種載荷組合，其中基本組合中包括2種載荷組合。標準給出了基本組合和偶然組合的表達式，規定了疲勞組合需要考慮的載荷但未給出表達式。

基本組合1：

基本組合2：

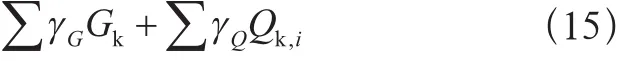
式中：

γG——永久載荷分項系數，式（14）中取1.35，

式（15）中取1.1；

γQ——可變載荷分項系數，1.35；

Gk——永久載荷標準值；

Qk,i——第i個可變載荷標準值。偶然組合：

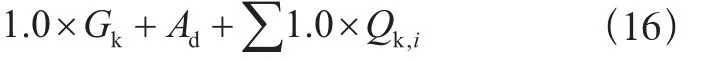
式中：

Ad——偶然載荷的設計值。

偶然載荷，例如地震載荷，只在有特殊要求時才需考慮。考慮偶然載荷時，采用式（16）所示組合，但考慮地震載荷時不需要同時考慮風載荷。

EN 13814: 2004規定，在進行結構疲勞分析時應當考慮作用位置變化的永久載荷、移動的外加載荷、驅動力和制動力、沖擊和振動載荷、預設碰撞力、離心力、科氏力等載荷，但是無須考慮雪載荷、溫度載荷、裝配載荷、不改變作用位置的永久載荷、不產生振動的風載荷，以及可變載荷中不隨時間和位置變化的分量；對于疲勞載荷產生的、組成疲勞設計應力譜的每一個應力分量的波動范圍，應乘以一個不小于1的疲勞載荷分項系數γFf，應力分量波動范圍之間不再施加組合系數；在疲勞強度校核部分，標準明確規定γFf取1.0。

在整體結構穩定性方面，EN 13814: 2004給出了防止傾覆、側滑和提升的設計表達式和分項安全系數。

防止傾覆：

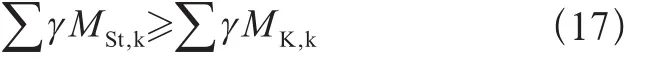
防止側滑（無地腳螺栓）：

防止側滑（有地腳螺栓）：

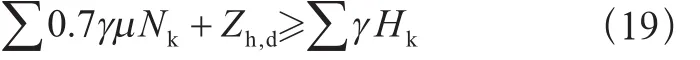
防止提升（無地腳螺栓）：

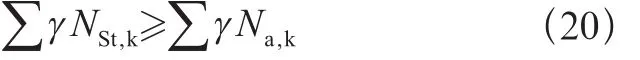
防止提升（有地腳螺栓）：

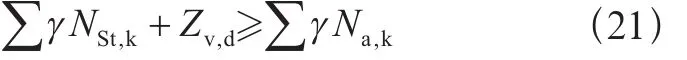
式中：

Hk——水平載荷分量；

Nk——垂直載荷分量；

Na,k——垂直提升載荷；

NSt,k——垂直穩定載荷；

MK,k——傾覆力矩；

MSt,k——穩定力矩；

Zh,d——地腳螺栓的水平承載能力；

Zv,d——地腳螺栓的垂直承載能力；

μ——摩擦系數；

γ——分項安全系數，見表1。

表1 穩定性分析分項安全系數

●2.2.2 ASTM F2291—17

ASTM F2291—17沒有明確給出極限狀態法的載荷組合公式，設計人員可以參考游樂設施使用地認可的、現行國家建筑標準中的載荷組合公式，這些標準包括但不限于：《國際建筑規范》第16章“結構設計”、ANSI/ AISC 360—05 《美國鋼結構設計規范》、ASCE/SEI 7—05 《美國建筑載荷設計規范》、《加拿大建筑規范》、《歐洲結構規范》等。如果當地沒有認可的國家建筑規范，載荷組合按照ASCE/ SEI 7—05《美國建筑載荷設計規范》。

下面以ASCE/SEI 7—05 《美國建筑載荷設計規范》為例，介紹其載荷組合。該規范第2章規定了7種基本載荷組合[11]。

基本組合1：

基本組合2：

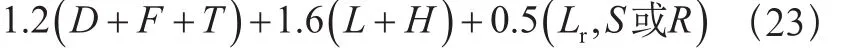
基本組合3：

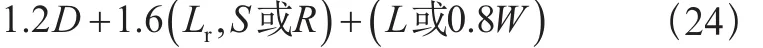
基本組合4：

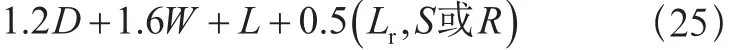
基本組合5：

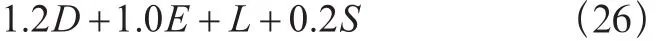
基本組合6：

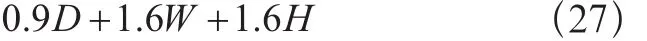
基本組合7：

式中：

D——永久載荷；

E——地震載荷；

F——流體壓力和液柱靜壓力載荷；

H——側向土、地下水或散裝物料壓力載荷；

L——活載荷（指乘員或用戶載荷）；

Lr——屋頂活載荷；

R——雨載荷；

S——雪載荷；

T——溫度載荷；

W——風載荷。

除了上述7種基本組合外，ASCE/SEI 7—05 《美國建筑載荷設計規范》還規定了包含洪水載荷的載荷組合和包含環境冰載荷的載荷組合。

當結構位于洪水高危區域時，應采用1.6W+2.0Fa代替式（25）和式（27）中的1.6W；當結構位于洪水區域但非高危區域時，應采用0.8W+1.0Fa代替式（25）和式（27）中的1.6W，其中Fa為洪水載荷。

當結構承受環境冰載荷時，應采用0.2Di+0.5S代替式（23）中的0.5(Lr，S或R)，采用Di+Wi+0.5S代替式（25）中的 1.6W+0.5(Lr，S 或 R)，采用 Di+Wi代替式（27）中的1.6W，其中Di為冰載荷、Wi為考慮結構裹冰后的風載荷。

疲勞分析時，應當考慮可能產生最大應力、應變波動范圍的載荷組合形式；除動載荷沖擊系數不小于1.2外，對所有其他疲勞載荷施加1.0的載荷分項系數。該標準明確指出采用1.0的載荷分項系數是因為疲勞相關載荷都是取預計可能出現的最大值，并且疲勞許用應力值不是平均值或者典型值，而是平均值減去2倍標準差后的設計值。

對于穩定性分析，ASTM F2291—17僅原則規定移動式游樂設施在安裝和運行時應能保持穩定、防止傾覆，并且需要考慮所有最不利的工況，例如不平衡載荷、風載荷等。但是，標準未對固定式游樂設施的穩定性提出要求，也未規定移動式游樂設施穩定性分析的設計表達式和安全系數。

2.3 規定的抗力系數

●2.3.1 EN 13814: 2004

對于靜強度，EN 13814: 2004強度校核部分規定，鋼制機械部件的抗力設計值應當滿足：

式中：

fy——標準規定的材料屈服強度；

fu——標準規定的材料抗拉強度；

γMy——抗力分項系數（屈服強度），取1.1；

γMu——抗力分項系數（抗拉強度），取1.35。

材料抗力設計值采用兩式中的較小者。對于橫向力和扭矩產生的剪切應力，材料抗力設計值還應當乘以α=0.58的系數。

對于疲勞強度，EN 13814: 2004強度校核部分規定，鋼材的疲勞抗力分項系數應根據斷裂后果和定期檢驗難度，按表2取值。

表2 疲勞抗力分項系數

●2.3.2 ASTM F2291—17

ASTM F2291—17并未明確給出材料靜強度抗力系數的值，只是規定可以從合適的載荷抗力系數法參考文獻中選取材料抗力系數和名義強度。如果按照美國鋼結構協會的《載荷和抗力系數設計規范》[12]，抗拉鋼結構的抗力設計值等于0.9倍屈服強度或者0.75倍抗拉強度，相當于屈服強度抗力分項系數取1.11、抗拉強度抗力分項系數取1.33；對于抗彎鋼梁，按照屈曲極限狀態設計，屈服強度抗力分項系數也為1.11。

關于鋼材疲勞強度，ASTM F2291—17規定可以直接采用美國焊接學會或者其他被美國認可標準中的疲勞強度數據，這些數據中已經包含了疲勞抗力安全系數。但是，對于其他基于平均值的疲勞數據，使用前應當進行修正，例如采用疲勞應力平均值減去2倍標準差的方法調整可以將疲勞失效概率降低至2.3%。

2.4 標準比對

ASTM F2291—17規定可以采用極限狀態設計法或者許用應力法，兩種方法并行可用，具體選擇哪種方法由用戶決定；標準未明確規定載荷組合公式、設計分項系數等設計所需關鍵信息；引用的相關設計標準范圍很廣，選用不同引用標準設計的結構難以保證具有一致的安全可靠度。上述情況可能與ASTM標準屬性有關，ASTM標準實質上是自愿性團體標準[13]，本身不具備強制力，因此標準中保留了多種方法和并行選項，具體選擇由標準用戶決定，只要保證設備安全即可。

EN 13814: 2004只允許采用極限狀態設計法，并明確給出了載荷組合公式、載荷分項系數和抗力分項系數等關鍵設計信息，這樣可以保證設計出來的游樂設施具有盡可能一致的安全可靠度。原因一方面很可能是由于EN標準的主要目標就是致力于消除歐盟境內貿易技術障礙以構建統一市場，另一可能的原因是歐洲建筑、土木等工程結構行業均已經強制采用極限狀態法，極限狀態法在歐洲已有很好的應用基礎和接受程度。總體上來說，EN 13814: 2004標準在極限狀態法方面更加系統和明確，并且有《歐洲結構規范》作為強有力的技術支撐。

3 建議和意見

鑒于目前歐洲和美國兩大國際主要游樂設施標準以及國內建筑、鋼結構、起重機械等工程結構設計標準均已采納引入了極限狀態設計方法，我國應當加快開展基于極限狀態法的游樂設施設計計算方法研究，建立典型游樂設施承載結構的極限狀態設計計算方法并應用示范，在此基礎上推動中國游樂設施標準中引入極限狀態設計法，為設計建造安全輕量、節材節能的游樂設施提供重要技術支撐。

為了建立基于極限狀態法的游樂設施設計計算方法，有以下工作需要進一步開展研究：

1）消化吸收國內外已有極限狀態設計方法，掌握極限狀態法的理論基礎和前提假設，特別是要弄清基本隨機變量的概率分布類型和特性、目標失效概率等用于確定分項安全系數的關鍵依據。

2）開展我國游樂設施主要載荷和典型材料性能的數據收集、試驗測試和統計分析，確定主要載荷參數和典型材料性能參數的概率分布類型和統計特征值，提出規范設計值。

3）開展我國游樂設施極限狀態設計計算模型研究，確定游樂設施承載極限狀態和正常使用極限狀態設計表達式，基于目標可靠指標提出游樂設施極限設計分項系數。

4）開展游樂設施極限狀態設計法應用示范，通過數值仿真、試驗測試等方法綜合驗證設計安全性。

上述研究工作中如何科學合理確定游樂設施復雜動態載荷的概率分布和統計特征值，進而確定合適的分項安全系數將會是游樂設施極限狀態設計方法研究的難點，需要重點研究。

參考文獻

[1]GB 8408—2008 游樂設施安全規范[S]．

[2]ISO 2394： 2015 General principles on reliability for structures[S]．

[3]GB 50153—2008 工程結構可靠性設計統一標準[S]．

[4]武清璽．結構可靠度、理論、方法及應用[M]．北京：科學出版社，2014：39-44．

[5]European Commission．Time line[EB/OL]．http：//eurocodes．jrc．ec．europa．eu/showpage．php?id=12．

[6]EN 13001-1： 2004 Cranes-General Design Part 1：General principles and requirements[S]．

[7]高策，薛吉崗．鐵路橋梁結構設計規范由容許應力法轉換為極限狀態法的思考[J]．橋梁，2012（02）：41-45．

[8]GB/T 3811—2008 起重機設計規范[S]．

[9]EN 13814： 2004 Fairground and amusement park machinery and structures-Safety[S]．

[10]ASTM F2291—17 Standard practice for design of amusement rides and devices[S]．

[11]ASCE/SEI 7—05 Minimum design loads for buildings and other structures[S]．

[12]AISC Manual of steel construction： load and resistance factor design(third edition)[S]．

[13]周立軍，王美萍．國外團體標準發展經驗研究——以ASTM國際標準組織為例[J]．標準科學，2016（10）：106-110．