基于自適應滑模觀測器的風機齒輪箱故障估計

章 敏， 文傳博

(上海電機學院 電氣學院， 上海 201306)

隨著風電技術的提高以及世界各國對風力發電采取的一系列鼓勵政策，使得世界范圍內的風電裝機容量逐年增大[1]。但是隨著風機的不斷運行，它的故障率也逐漸增加[2-3]。齒輪箱作為風電機組傳動系統的執行元件，其發生故障會導致傳動系統不能穩定工作，從而影響風機的正常運行。故障估計不僅能夠檢測出部件是否發生故障，并且還能夠診斷出產生故障的形式，便于故障維修。

目前，基于滑模觀測器的故障估計研究內容較多且較豐富。文獻[4]中針對一類Lipschitz非線性系統的執行器故障估計問題，提出了一種基于二階滑模觀測器的故障估計方法。文獻[5]中針對一類不確定非線性系統的傳感器故障估計問題，將傳感器故障相量轉化為僅存在執行器故障和未知輸入的增廣廣義系統，針對所構造的奇異系統，設計了一種魯棒滑模觀測器來估計原系統的傳感器故障。文獻[6]中針對一類線性不確定時變時滯系統，設計了一種新的滑模觀測器，并在此基礎上，提出了一種魯棒執行器故障估計方法。文獻[7]中針對系統存在多故障的情況，利用自適應滑模觀測器實現故障估計。文獻[8]中提出了一種廣義滑模觀測器，并利用等效注入的方法實現故障估計。文獻[9]中則分析了將滑模觀測器應用到風力發電系統的執行器的故障估計問題。Tan等[10]針對系統的執行器存在緩變故障的問題，提出了一種故障估計方法，但并沒有充分考慮到系統存在未知干擾的情況。由于滑模變結構對擾動具有很強的魯棒性[11]，故本文將滑模觀測器與文獻[10]中提出的自適應估計算法相結合構成自適應滑模觀測器，用于實現傳動系統的齒輪箱故障估計。最后，通過仿真表明利用該方法實現齒輪箱的故障估計的魯棒性更好。

1 風電機組傳動系統的建模

1.1 葉輪模型

根據貝茲理論，得葉輪所吸收的風能功率[12]為

(1)

式中：ρ為空氣密度;V為實際風速曲線;R為葉輪半徑;Cp(λ,β)為葉輪的功率系數，表示葉輪捕獲風能的特性，它與槳距角β和葉尖速比λ有關。

風輪機的葉尖速比λ與葉輪轉子角速度ω以及風速有關，其表達式為

λ=Rω/V

(2)

由式(1)和式(2)得葉輪的氣動轉矩為

(3)

由氣動轉矩表達式可知，傳動系統的輸入轉矩Tr隨外界風速而變化，而外界風速極不穩定，因此Tr具有很強的不確定性。

1.2 傳動系統軸系模型

傳動系統軸系模型一般分為剛性軸模型和柔性軸模型[13]，本文選用最常用的剛性軸模型為研究對象，剛性軸模型認為由低速軸向高速軸傳遞的過程，是按照齒輪箱的傳動比傳動。剛性軸模型的受力如圖1所示，將低速軸和高速軸看成為兩個質量塊，且它們與齒輪箱之間的轉動慣量忽略不計。

圖1 剛性軸模型的受力示意圖

傳動系統實際上可看成輸入為葉輪的氣動轉矩Tr，輸出為發電機電磁轉矩Te。根據圖1模型，可建立動力學方程

Tr-NTe=(Jr+NJg)(ωg/N)

(4)

式中：N為齒輪箱傳動比;Jr為葉輪轉子轉動慣量;ωg為電機轉速;Jg為高速軸轉動慣量。

1.3 發電機模型

發電機模型是建立傳動系統模型的重要一環，發電機的動態方程反映的是轉矩與轉速之間的關系，通過它們的關系方程再與傳動軸方程聯立求解即可得出傳動系統的數學模型。本文研究的風機為恒速風力發電機，其特點是葉輪轉速保持恒定，具有維護少、直接并網等特點。恒速風力機選用的發電機一般為恒速感應式發電機，該發電機的電磁轉矩不僅與轉速有關，還與轉速的變化率有關，它們之間的關系可以表示為

(5)

式中：De為發電機Te與ωg曲線圖的斜率;τ為發電機的時間常數;ω0為同步轉速。

1.4 傳動系統的狀態空間模型

對式(5)進行二次求導后代入式(4)，再經Laplace變換后，可得傳動系統的傳遞函數為

(6)

將式(6)轉化成狀態空間模型時應考慮建模誤差及未知輸入的影響，因此，傳動系統的狀態空間模型為：

(7)

2 齒輪箱的故障估計

齒輪箱作為傳動系統的內部部件，當齒輪箱產生故障時，傳動系統的狀態空間模型變為

(8)

式中：fa(t)為齒輪箱故障信號;E為故障分布矩陣。

針對傳動系統式(8)，現作如下假設：

假設1系統是可觀的，則存在反饋矩陣L∈R2×1，使得A0=A-LC的特征根均具有負實部。

假設3存在矩陣F，使得PD=CTFT。

基于假設1～5，設計自適應滑模觀測器如下：

(9)

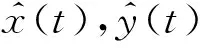
(10)

式中：β為正常數;F滿足假設3;δ是標量非常小的常數，設計δ的目的是為了避免系統發生抖振現象[14]。

滑模控制律用來抑制擾動的影響，使得殘差只包含故障的信息，根據殘差信號可設計故障估計自適應律算法，其表達式為[10]

(11)

式中：E0為待設計的適維矩陣，滿足假設5。

(12)

證明選取Lyapunov函數

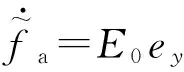
因此，通過以上滑模觀測器的設計以及故障估計算法可以有效地實現齒輪箱的故障估計。傳動系統齒輪箱的故障估計設計如圖2所示。

圖2 齒輪箱故障估計的設計框圖

3 仿真分析

某300 kW風力發電機的各項參數[15]見表1。

表1 300 kW風力發電機仿真參數

將上述參數代入傳動系統方程得系數矩陣：

由矩陣A和C知系統是可觀的，故將觀測器的兩個極點都配置在-10。通過計算得反饋矩陣

針對齒輪箱齒面磨損引起的漂移故障，分別設計自適應觀測器和自適應滑模觀測器進行故障估計，驗證后者的估計效果更好，設計故障表達式為：

(13)

自適應觀測器與自適應滑模觀測器相比，少了滑模控制律函數，針對傳動系統，設計自適應觀測器如下：

(14)

設計實驗的各項參數為：

基于自適應觀測器的齒輪箱漂移故障估計及估計誤差分別如圖3和圖4所示。基于自適應滑模觀測器的漂移故障估計及估計誤差分別如圖5和圖6所示。

圖3 基于自適應觀測器的齒輪箱漂移故障估計

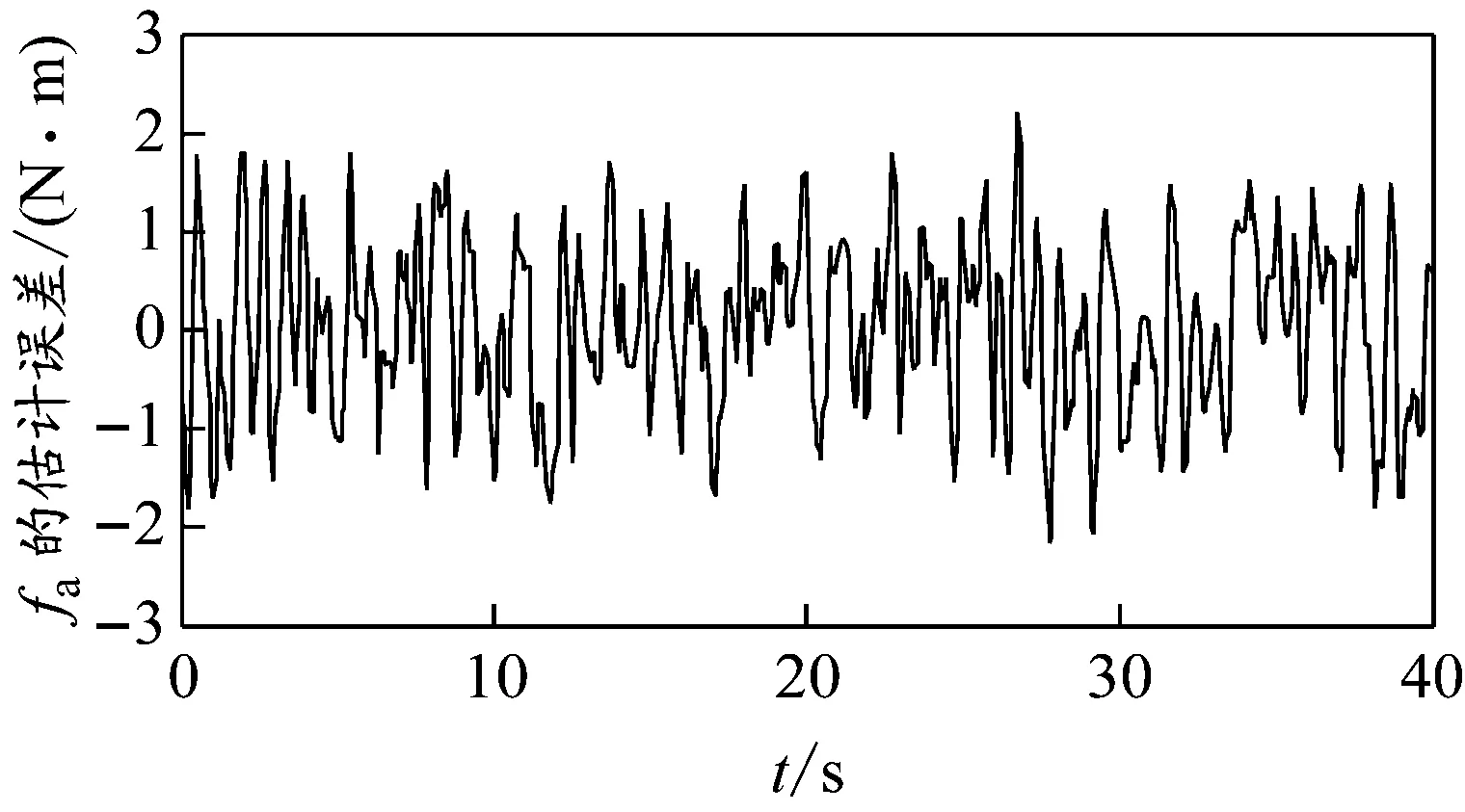
圖4 基于自適應觀測器的齒輪箱漂移故障估計誤差

通過仿真圖3和圖5可以看出，兩者均能大致地估計出故障的狀態，從而說明所設計的故障估計算法的有效性。從圖4和圖6可以看出，基于自適應滑模觀測器的故障估計精度要高，說明針對存在擾動和齒輪箱故障的傳動系統，利用自適應滑模觀測器實現齒輪箱故障估計的魯棒性更好。

圖5 基于自適應滑模觀測器的齒輪箱漂移故障估計

圖6 基于自適應滑模觀測器的齒輪箱漂移故障估計誤差

4 結 語

本文針對有擾動和齒輪箱故障的風電機組傳動系統，提出了一種基于自適應滑模觀測器的故障估計方法。首先建立了傳動系統的數學模型，由于建模誤差及未知輸入的影響，因此系統受到未知輸入擾動的干擾。然后針對含有擾動和齒輪箱故障的系統模型，設計一類自適應滑模觀測器用來實現齒輪箱的故障估計，利用李雅普諾夫穩定性原理證明了故障估計方法的正確性。最后分別對基于自適應觀測器和自適應滑模觀測器的兩種故障估計方法進行仿真，仿真結果表明，針對有擾動的傳動系統，本文提出的故障估計方法的魯棒性更好。

參考文獻

[1] JAUCH C, SORENSEN P, NORHEIM I, et al. Simulation of the impact of wind power on the transient fault behavior of the Nordic power system[J].Electric Power Systems Research,2007,77(2):135-144.

[2] RIBRANT J, BERTLING L M. Survey of failures in wind power systems with focus on swedish wind power plants during 1997—2005[J].IEEE Transactions on Energy Conversion, 2007,22(1):167-173.

[3] 張鎮,關書強.風電機組故障統計分析研究[J].風能,2013(8):74-77.

[4] HU Zhenggao,ZHAO Guorong,ZHANG Lei,et al. Fault estimation for nonlinear dynamic system based on the second-order sliding mode observer[J]. Circuits Systems and Signal Processing,2016,35(1):101-115.

[5] YANG Junqi,ZHU Fanglai,WANG Xin,et al. Robust sliding-mode observer-based sensor fault estimation, actuator fault detection and isolation for uncertain nonlinear systems[J]. International Journal of Control, Automation and Systems,2015,13(5):1037-1046.

[6] BOULAABI I,SELLAMI A.Robust delay-derivative-dependent sliding mode observer for fault reconstruction: a diesel engine system application[J]. Birkhauser Boston Inc.,2016,35(7):2351-2372.

[7] 劉聰,李穎暉,吳辰,等.基于魯棒自適應滑模觀測器的多故障重構[J].控制與決策,2016,31(7):1219-1224.

[8] 穆凌霞,余翔,李平,等.自適應廣義滑模觀測器之狀態估計和故障重構[J].控制理論與應用,2017,34(4):483-490.

[9] 沈艷霞,賀慶楠,楊雄飛,等.風能轉換系統執行器故障重構與容錯控制[J].控制理論與應用,2015,32(12):1698-1704.

[10] TAN C P, EDWARDS C. Sliding mode observers for detection and reconstruction of sensor faults[J].Automatica,2002, 38(10):1815-1821.

[11] 李卓,盧子廣.基于滑模觀測器的異步電機無速度傳感器控制[J].電氣傳動,2016,46(7):12-15.

[12] 高峰,徐大平,呂躍剛.基于葉素理論的風力發電機組風輪建模[J].現代電力,2007,24(6):52-57.

[13] MUYEEN S M，ALI M H，TAKAHASHI R，et al. Comparative study on transient stability analysis of wind turbine generator system using different drive train models[J].Renewable Power Generation Let,2007,1(2):131-141.

[14] UTKIN V I. Sliding modes in control and optimization[J].Springer Berlin Heidelberg, 1992,189(3):1372-1379.

[15] 劉豹.風力發電機傳動裝置建模分析[D].沈陽:東北大學, 2012.