用對數(shù)函數(shù)描述收斂因子的改進(jìn)灰狼優(yōu)化算法及其應(yīng)用

伍鐵斌，桂衛(wèi)華，陽春華，龍文，李勇剛，朱紅求

?

用對數(shù)函數(shù)描述收斂因子的改進(jìn)灰狼優(yōu)化算法及其應(yīng)用

伍鐵斌1, 2，桂衛(wèi)華1，陽春華1，龍文3，李勇剛1，朱紅求1

(1. 中南大學(xué) 信息科學(xué)與工程學(xué)院，湖南 長沙，410083；2. 湖南人文科技學(xué)院 能源與機(jī)電工程學(xué)院，湖南 婁底，417000；3. 貴州財(cái)經(jīng)大學(xué) 貴州省經(jīng)濟(jì)系統(tǒng)仿真重點(diǎn)實(shí)驗(yàn)室，貴州 貴陽，550025)

針對灰狼優(yōu)化(grey wolf optimization, GWO)算法在求解復(fù)雜高維優(yōu)化問題時(shí)存在解精度低、易陷入局部最優(yōu)等缺點(diǎn)，提出一種基于對數(shù)函數(shù)描述收斂因子的改進(jìn)GWO算法。采用佳點(diǎn)集方法初始化種群以保證個(gè)體盡可能均勻地分布在搜索空間中；提出一種基于對數(shù)函數(shù)描述的非線性收斂因子替代線性遞減收斂因子，以協(xié)調(diào)算法的勘探和開采能力；對當(dāng)前最優(yōu)的3個(gè)個(gè)體執(zhí)行改進(jìn)的精英反向?qū)W習(xí)策略產(chǎn)生精英反向個(gè)體，以避免算法出現(xiàn)早熟收斂。研究結(jié)果表明改進(jìn)算法具有較好的尋優(yōu)性能。

灰狼優(yōu)化算法；對數(shù)函數(shù)；收斂因子

群體智能算法可以求解目標(biāo)函數(shù)(或約束)不連續(xù)或不可微的優(yōu)化問題，得到了越來越多的研究與應(yīng) 用[1]。典型的群體智能算法主要有微粒群算法[2]、遺傳算法[3]、差分進(jìn)化算法(differential evolution, DE)[4]，近年來一些學(xué)者又提出了布谷鳥算法[5]、蝙蝠算法[6]和灰狼優(yōu)化算法(grey wolf optimization, GWO)[7]等新的智能算法。GWO是受灰狼群體等級制度和狼群跟蹤、包圍、追捕與攻擊獵物的捕食行為啟發(fā)而提出的智能算法，求解精度和收斂速度均優(yōu)于微粒群算法、差分進(jìn)化算法和引力搜索算法[7]。GWO算法已經(jīng)應(yīng)用于多級閾值圖像分割[8]、電力潮流優(yōu)化[9]、水量分配[10]、PID控制參數(shù)優(yōu)化[11]、無人機(jī)路徑規(guī)劃[12]等眾多領(lǐng)域。然而，GWO算法與其他群體智能優(yōu)化算法一樣，存在求解精度低、易出現(xiàn)早熟收斂等缺點(diǎn)，因此，許多研究者對GWO算法進(jìn)行了改進(jìn)，如SAREMI等[13]將動(dòng)態(tài)進(jìn)化種群技術(shù)與GWO相結(jié)合，仿真結(jié)果表明改進(jìn)后的GWO算法的全局尋優(yōu)能力得到提高；龍文 等[14]利用混沌的方法產(chǎn)生GWO的初始種群以保持個(gè)體多樣性，并引入反向?qū)W習(xí)策略，將改進(jìn)的GWO算法用于求解高維優(yōu)化問題；徐松金等[15]提出了一種融合遺傳算子的改進(jìn)GWO算法，仿真驗(yàn)證了算法的有效性；徐達(dá)宇等[16]構(gòu)建基于自組織臨界優(yōu)化的改進(jìn) GWO 算法，利用標(biāo)準(zhǔn)測試函數(shù)驗(yàn)證了算法的全局尋優(yōu)能力。針對基本GWO算法的缺點(diǎn)，本文作者提出一種改進(jìn)GWO算法，采用佳點(diǎn)集方法初始化種群個(gè)體；基于對數(shù)函數(shù)對收斂因子公式進(jìn)行改進(jìn)，提出一種非線性收斂因子以平衡算法的探索和開發(fā)能力，并對當(dāng)前最好的3個(gè)個(gè)體狼、狼和狼執(zhí)行改進(jìn)的精英反向?qū)W習(xí)策略產(chǎn)生新個(gè)體。利用標(biāo)準(zhǔn)測試函數(shù)和針鐵礦沉鐵過程的參數(shù)優(yōu)化驗(yàn)證改進(jìn)的GWO算法的有效性。

1 基本灰狼優(yōu)化算法

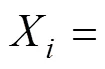
對第只灰狼第維位置，通過下式描述灰狼逐漸接近并包圍獵物的行為：

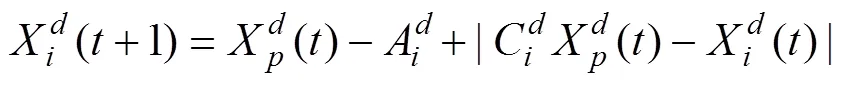
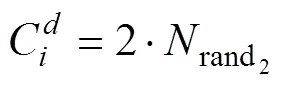
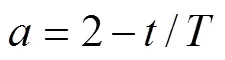
式中：為最大迭代次數(shù)。

由2線性遞減至0，該參數(shù)起到調(diào)節(jié)算法的全局搜索與局部搜索的作用。

群體中的各個(gè)狼根據(jù)與，和的位置即，和的距離進(jìn)行更新：

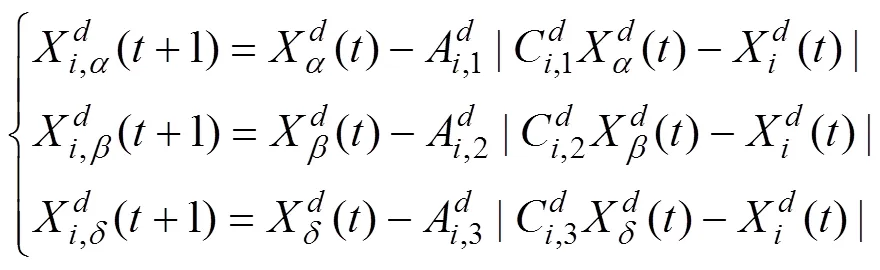
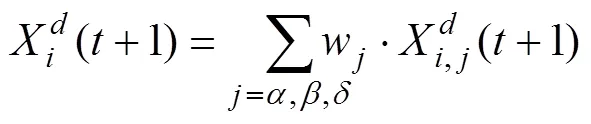
式中：w=(=，，)為，，的權(quán)重系數(shù)；=1，2，…，。

式中：(X())為第只灰狼在第代的適應(yīng)度；(())，(())和(())分別為第代首領(lǐng)狼、副首領(lǐng)狼和普通狼的適應(yīng)度。GWO算法的偽代碼見文獻(xiàn)[7]。

2 改進(jìn)的灰狼優(yōu)化算法

2.1 佳點(diǎn)集種群初始化

初始種群多樣性會影響群體智能算法的全局收斂速度和解的質(zhì)量，多樣性較好的初始種群對提高算法的尋優(yōu)性能有幫助[17]。然而，標(biāo)準(zhǔn)GWO算法采用隨機(jī)的方法產(chǎn)生初始種群個(gè)體，難以保證初始群體的多樣性，會造成算法的尋優(yōu)效率降低。本文利用佳點(diǎn)集方法[18]產(chǎn)生初始種群，該方法能保證初始種群更均勻地分布在解空間中，實(shí)現(xiàn)方法如下。

2.2 基于對數(shù)函數(shù)的非線性收斂因子

對群體智能優(yōu)化算法來說，如何協(xié)調(diào)其勘探能力和開采能力至關(guān)重要。勘探意味著群體需要探測更廣泛的搜索區(qū)域，避免算法陷入局部最優(yōu)。開采則強(qiáng)調(diào)充分利用已有的信息對群體的某些鄰域進(jìn)行密集搜索，對算法的收斂速度具有決定性的影響。勘探和開采類似于全局搜索和局部搜索。毫無疑問，只有當(dāng)群體智能優(yōu)化算法能夠較好地協(xié)調(diào)勘探能力和開采能力時(shí)，才能具備較強(qiáng)的魯棒性和較快的收斂速度。

由式(2)可知：當(dāng)||＜1時(shí)，灰狼群體將包圍圈縮小，攻擊并捕獲獵物，對應(yīng)于算法的局部開發(fā)能力；當(dāng)||＞1時(shí)，灰狼群體將包圍圈擴(kuò)大，探索更好的獵物；在很大程度上取決于收斂因子，即會影響算法的勘探能力和開采能力。由式(4)可知：在進(jìn)化過程中由2線性遞減到0。然而，GWO算法在搜索過程中卻是需要非線性變化的，收斂因子線性遞減策略不能滿足實(shí)際的優(yōu)化搜索過程。受PSO算法中慣性權(quán)重設(shè)置的啟發(fā)[19]，本文提出一種基于對數(shù)函數(shù)的非線性收斂因子更新公式，收斂因子在前期選取較大的值以加強(qiáng)算法的全局搜索能力。由于在尋優(yōu)初期的種群多樣性很好，故在尋優(yōu)前期以較快的速度減小，而在尋優(yōu)中期以較慢的速度減小，平衡算法的勘探與開采能力。的更新策略為

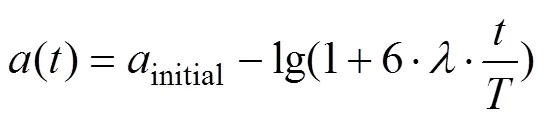
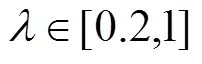
2.3 改進(jìn)的精英反向?qū)W習(xí)策略

在GWO算法的進(jìn)化后期，所有灰狼個(gè)體均向狼逼近(每次迭代保留最優(yōu)個(gè)體)，群體多樣性變差，收斂速度明顯變慢或早熟收斂，這也是群體智能優(yōu)化算法的固有缺點(diǎn)。由文獻(xiàn)[20]可知：精英反向?qū)W習(xí)策略能較好地?cái)U(kuò)大群體的搜索范圍，探索出新的搜索區(qū)域，增強(qiáng)群體的多樣性，將其與群體智能優(yōu)化算法混合，可提高混合算法的全局搜索能力和避免算法陷入局部最優(yōu)。由GWO算法機(jī)理可知：狼為當(dāng)前群體中的最優(yōu)個(gè)體，群體中其他個(gè)體均向其所在區(qū)域靠攏，若其為局部最優(yōu)解，則算法陷入局部最優(yōu)。因此，本文對當(dāng)前群體中的最優(yōu)的3個(gè)個(gè)體(狼、狼和狼)執(zhí)行改進(jìn)的精英反向?qū)W習(xí)策略以維持群體的多樣性，從而加強(qiáng)算法的全局探索能力和避免算法陷入局部最優(yōu)。

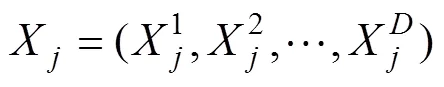
狼群的活性值為

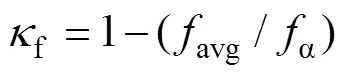
式中：avg為所有狼對應(yīng)的適應(yīng)度的平均值(假定適應(yīng)度都大于0，適應(yīng)度越大，則個(gè)體最優(yōu))；α為頭狼對應(yīng)的適應(yīng)度。顯然，f越小，即avg與α越接近，表明其他狼都非常接近頭狼，反映出狼群的多樣性已經(jīng)很差，也即群體的活性很差，此時(shí)，必須取1個(gè)較大的值，提高狼群的多樣性，保證狼群能有效的跳出局部最優(yōu)；反之，取1個(gè)較小的值。對最優(yōu)的3個(gè)個(gè)體(狼、狼和狼)都執(zhí)行次精英反向?qū)W習(xí)(為小于等于4的正整數(shù)，本文取=2)。

2.4 算法流程圖

改進(jìn)灰狼優(yōu)化算法(LFGWO)流程圖如圖1所示。

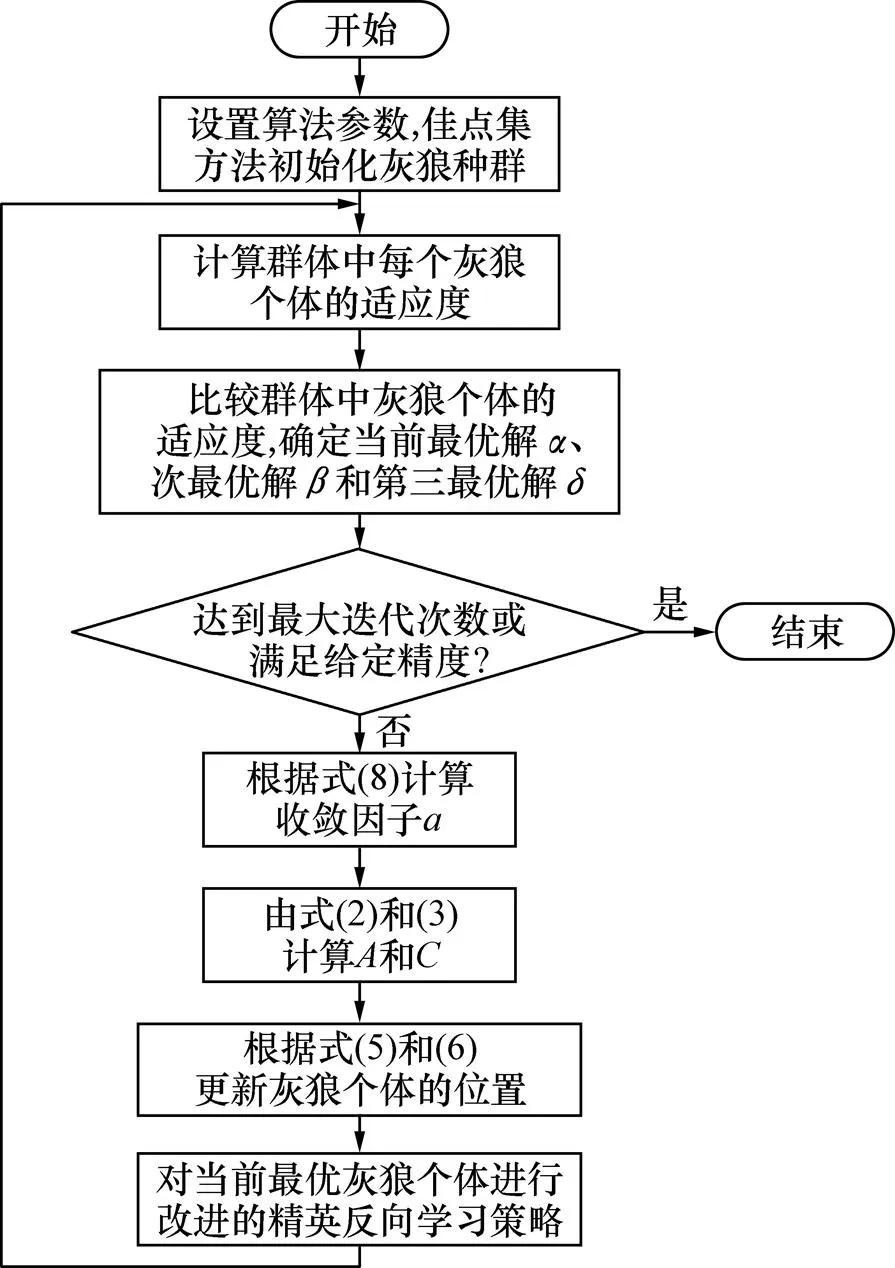
圖1 LFGWO算法流程圖

3 實(shí)驗(yàn)分析

3.1 測試函數(shù)

為了驗(yàn)證本文提出的基于對數(shù)函數(shù)的改進(jìn)灰狼優(yōu)化算法(記為LFGWO)的有效性，從文獻(xiàn)[7]中選取8個(gè)國際上通用的標(biāo)準(zhǔn)測試函數(shù)進(jìn)行數(shù)值實(shí)驗(yàn)，8個(gè)測試函數(shù)的函數(shù)名、具體表達(dá)式、搜索區(qū)間以及收斂精度如表1所示。在8個(gè)標(biāo)準(zhǔn)測試函數(shù)中，1~5為復(fù)雜單峰函數(shù)，6~8為復(fù)雜多峰函數(shù)，8個(gè)測試函數(shù)的維數(shù)均設(shè)置為30，8個(gè)函數(shù)的理論全局最優(yōu)值均為0。

3.2 與GWO和HGWO算法的比較

利用本文提出的LFGWO算法對上述8個(gè)標(biāo)準(zhǔn)測試函數(shù)進(jìn)行求解，并與標(biāo)準(zhǔn)GWO算法、hybrid GWO with differential evolution (記為HGWO)[20]算法進(jìn)行比較。為了比較的公平性，3種算法的參數(shù)設(shè)置如下：種群規(guī)模均設(shè)置為=30，最大迭代次數(shù)均設(shè)置為500，每個(gè)函數(shù)在上述參數(shù)設(shè)置下均獨(dú)立運(yùn)行30次，并記錄其最優(yōu)值、平均值、最差值和標(biāo)準(zhǔn)差，比較結(jié)果如表2所示，其中，HGWO算法的結(jié)果直接來源于參考文獻(xiàn)[20]。

從表2可以看出：除了Rosenbrock函數(shù)以外，LFGWO算法對其他7個(gè)標(biāo)準(zhǔn)測試函數(shù)30次實(shí)驗(yàn)一致地收斂到全局最優(yōu)解(當(dāng)收斂精度達(dá)到1×10?10時(shí)認(rèn)為算法收斂)，與基本GWO算法相比，LFGWO算法尋優(yōu)性能得到了顯著提高。與HGWO算法相比，LFGWO算法在5個(gè)函數(shù)即Sphere，Schwefel2.22，Schwefel1.2，Schwefel2.21和Ackley函數(shù)上取得了較好的尋優(yōu)結(jié)果；對于Rosenbrock函數(shù)，LFGWO算法獲得了較好的最差值和標(biāo)準(zhǔn)差，而HGWO算法取得了較好的最優(yōu)值和平均值；對于函數(shù)Rastrigin和Griewank，2種算法得到了相似的最優(yōu)值。

圖2所示為基本GWO算法和LFGWO算法對5個(gè)函數(shù)的尋優(yōu)收斂曲線。從圖2可以看出：與基本GWO算法相比，LFGWO算法具有更快的收斂速度和更高的收斂精度。

3.3 與其他改進(jìn)群體智能優(yōu)化算法的比較

為了進(jìn)一步說明LFGWO算法的有效性，將其與文獻(xiàn)[1]中的9種改進(jìn)群體智能優(yōu)化算法進(jìn)行比較，這9種算法為：SADE，jDE，JADE，CLPSO，HPSO，OLPSO，GABC，CABC和OCABC。為了比較的公平性，LFGWO算法的最大適應(yīng)度計(jì)算次數(shù)設(shè)置為 50 000次；SADE、jDE和JADE 3種算法的對每個(gè)函數(shù)設(shè)置了不同的適應(yīng)度計(jì)算次數(shù)，最少為50 000次，最多為300 000次；CLPSO，HPSO和OCPSO這3種算法的適應(yīng)度計(jì)算次數(shù)均設(shè)置為150 000次；GABC，CABC和OCABC 3種算法的適應(yīng)度計(jì)算次數(shù)均設(shè)置為200 000次。LFGWO算法與其他9種算法對6個(gè)測試函數(shù)(1，2，5，6，7，8)的尋優(yōu)結(jié)果比較如表3所示。為了增加可信度，其他9種算法的結(jié)果直接來源于文獻(xiàn)[1]。

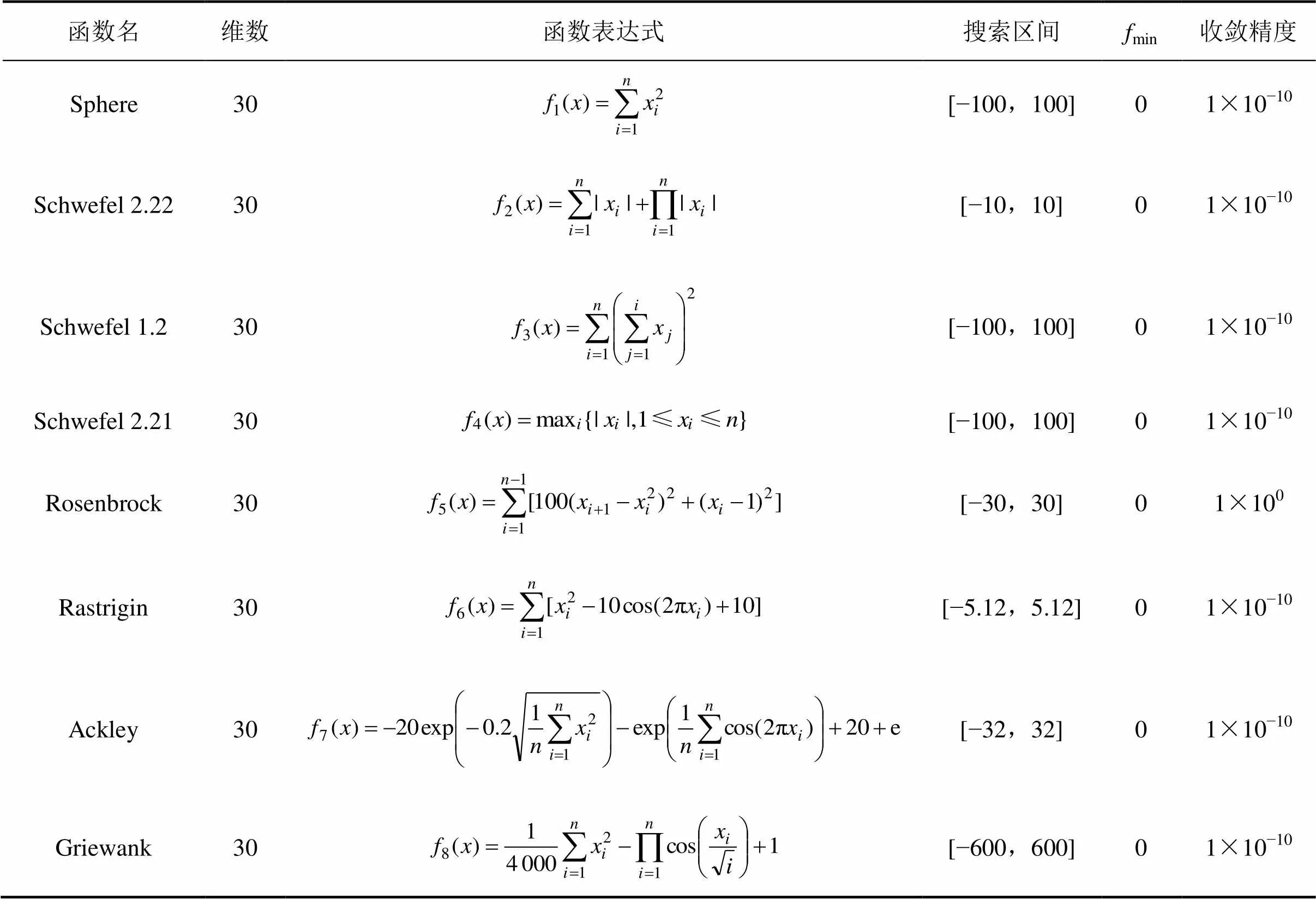
表1 8個(gè)標(biāo)準(zhǔn)測試函數(shù)

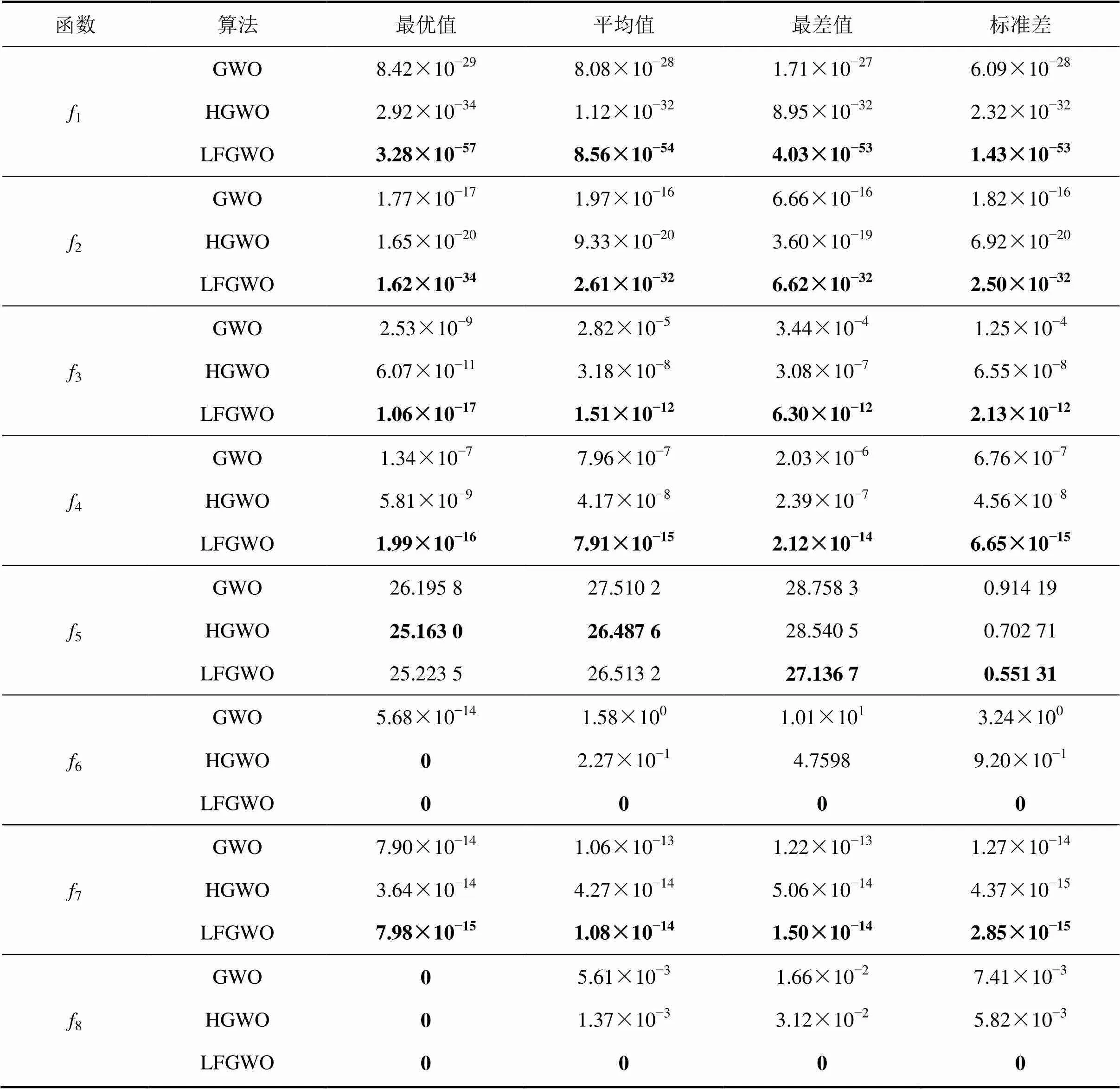
表2 3種算法對8個(gè)函數(shù)的尋優(yōu)結(jié)果比較

注：表中黑粗體表示比較算法中的最好結(jié)果。

從表3可知：與SaDE，jDE，JADE，CLPSO，HPSO，OLPSO和GABC算法相比，除了Rosenbrock(5)函數(shù)外，LFGWO算法在其他5個(gè)測試函數(shù)上均獲得了較好的平均值和標(biāo)準(zhǔn)差。與CABC算法相比，LFGWO算法在4個(gè)函數(shù)(1，2，7，8)上獲得了較好的結(jié)果，在函數(shù)5上得到了較差的結(jié)果，在函數(shù)6上取得了相似的結(jié)果。與OCABC算法相比，LFGWO算法在2個(gè)函數(shù)(1，2)上獲得了較好的結(jié)果，在3個(gè)函數(shù)(6，7，8)上取得了相似的結(jié)果。

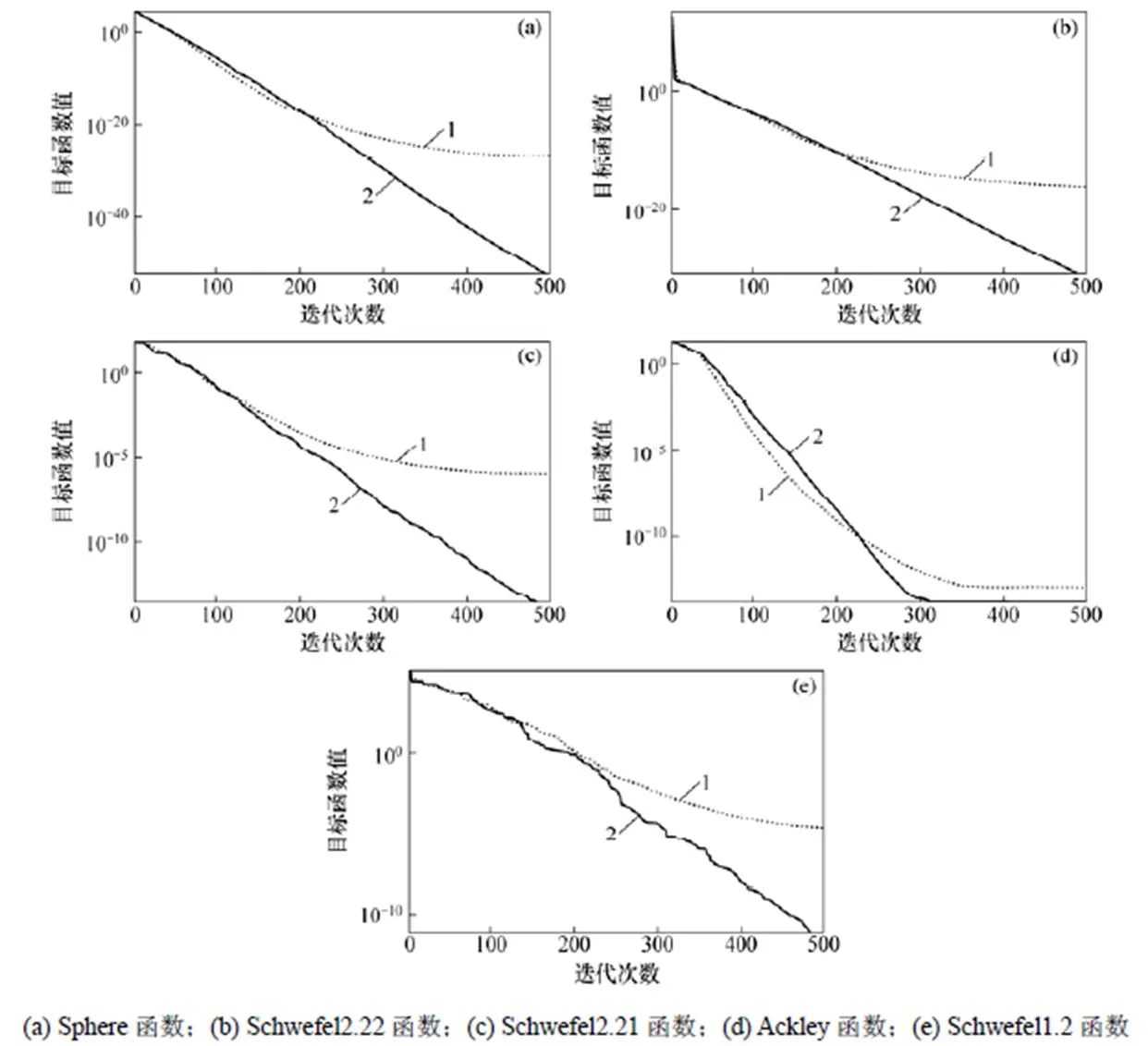
圖2 GWO和LFGWO對5個(gè)函數(shù)的尋優(yōu)收斂曲線

表3 LFGWO算法與其他9種算法對6個(gè)函數(shù)的結(jié)果比較

注：表中黑粗體表示比較算法中的最好結(jié)果。

4 工業(yè)優(yōu)化應(yīng)用

在濕法煉鋅生產(chǎn)過程中，必須將浸出的硫酸鋅溶液中的鐵離子降低至合適范圍，針鐵礦沉鐵法是通過向5個(gè)連續(xù)的反應(yīng)器中加入氧氣，使溶液中的二價(jià)鐵離子逐漸氧化為三價(jià)鐵離子；氧氣添加量過多，不容易生成針鐵礦的沉淀物。而若氧化速率過慢，則會導(dǎo)致沉鐵后的溶液中鐵離子濃度超標(biāo)。為保證良好的針鐵礦沉鐵環(huán)境，通過向各反應(yīng)器中添加成本低的鋅焙砂控制各反應(yīng)器的pH。文獻(xiàn)[21]建立了針鐵礦沉鐵過程的優(yōu)化模型：

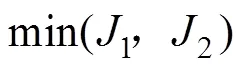
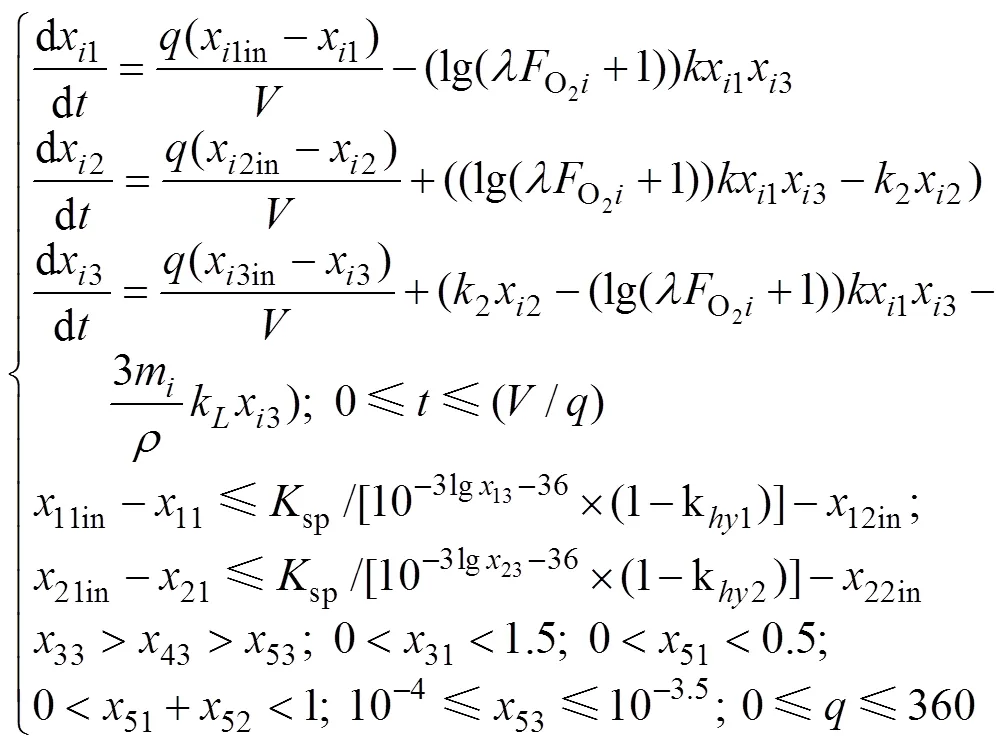
由于1和2的量綱不一樣，故對1進(jìn)行歸一化處理：

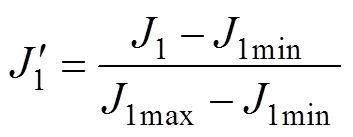
對目標(biāo)函數(shù)進(jìn)行加權(quán)處理[21]，即轉(zhuǎn)換為

式中：1+2=1，在這里取1=0.5，2=0.5。

利用本文提出的改進(jìn)灰狼算法對文獻(xiàn)[21]提出的4種典型工況進(jìn)行尋優(yōu)，結(jié)果如表4所示，氧氣添加量的優(yōu)化值如表5和表6所示。

從表6可知：在4種典型針鐵礦沉鐵工況下，本文提出的改進(jìn)灰狼算法優(yōu)化的氧氣添加量比實(shí)際工業(yè)過程的氧氣添加量分別減少了19.82%，19.99%，22.12%和21.13%，比文獻(xiàn)[21]提出的雙種群協(xié)同進(jìn)化算法分別減少氧氣1.82%，1.59%，0.22%和1.93%。

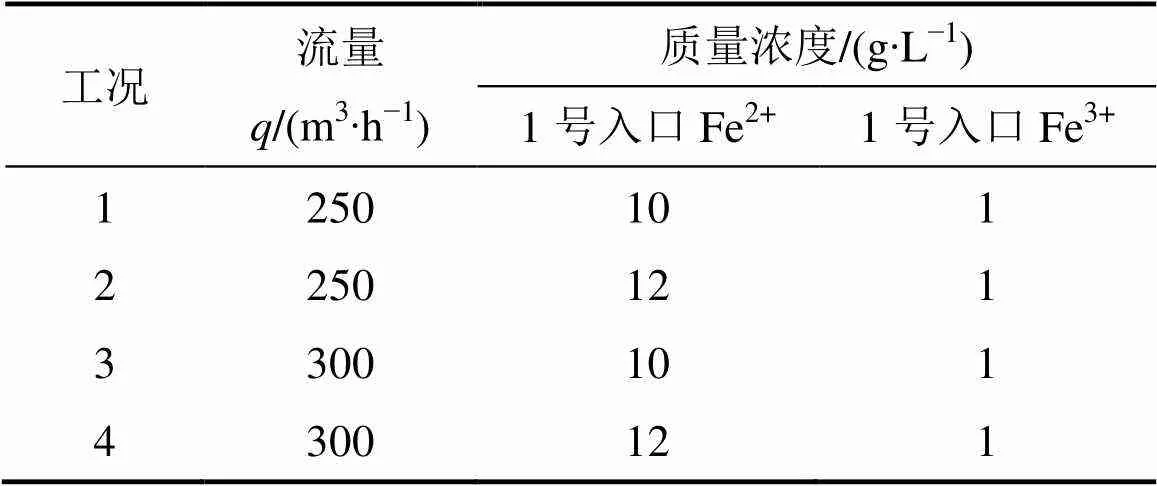
表4 針鐵礦法沉鐵過程典型工況分類表[21]

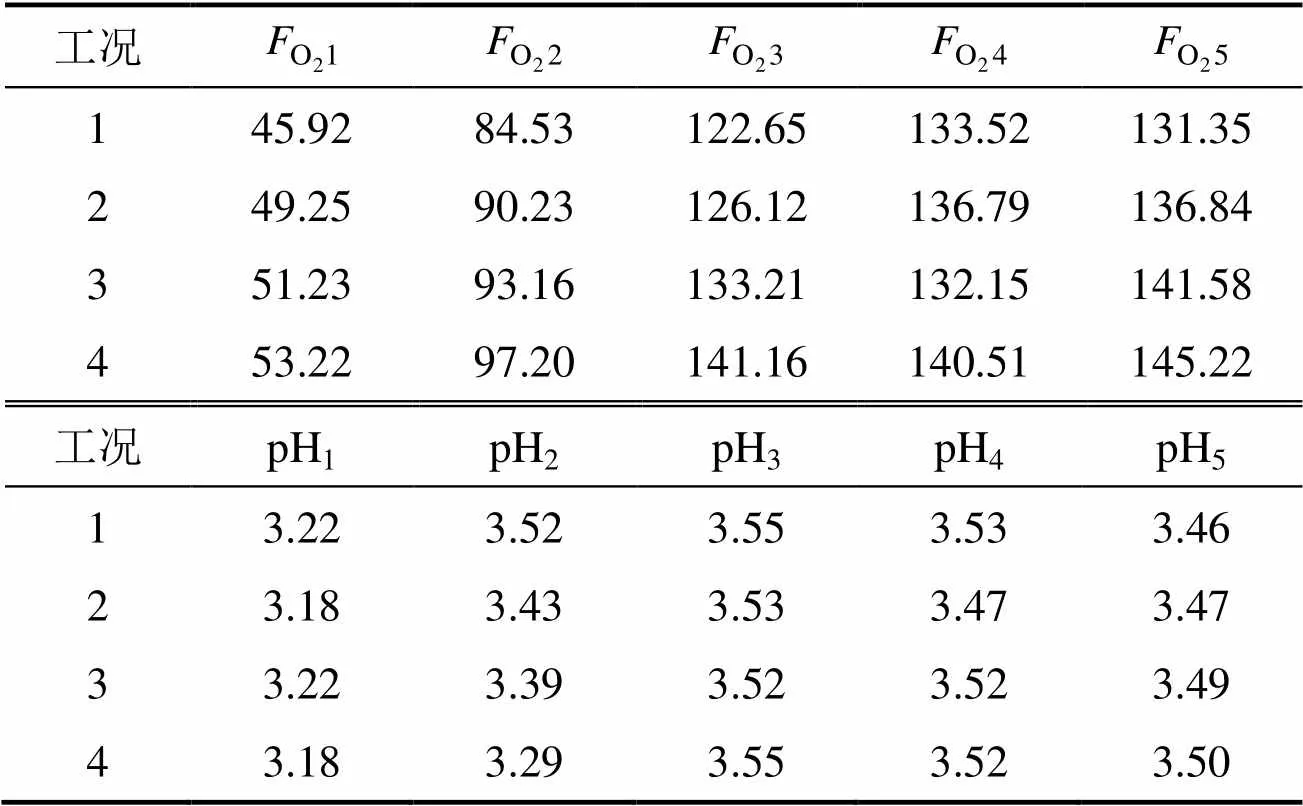
表5 基于改進(jìn)灰狼算法的氧氣添加量優(yōu)化結(jié)果(10次優(yōu)化結(jié)果的平均值)

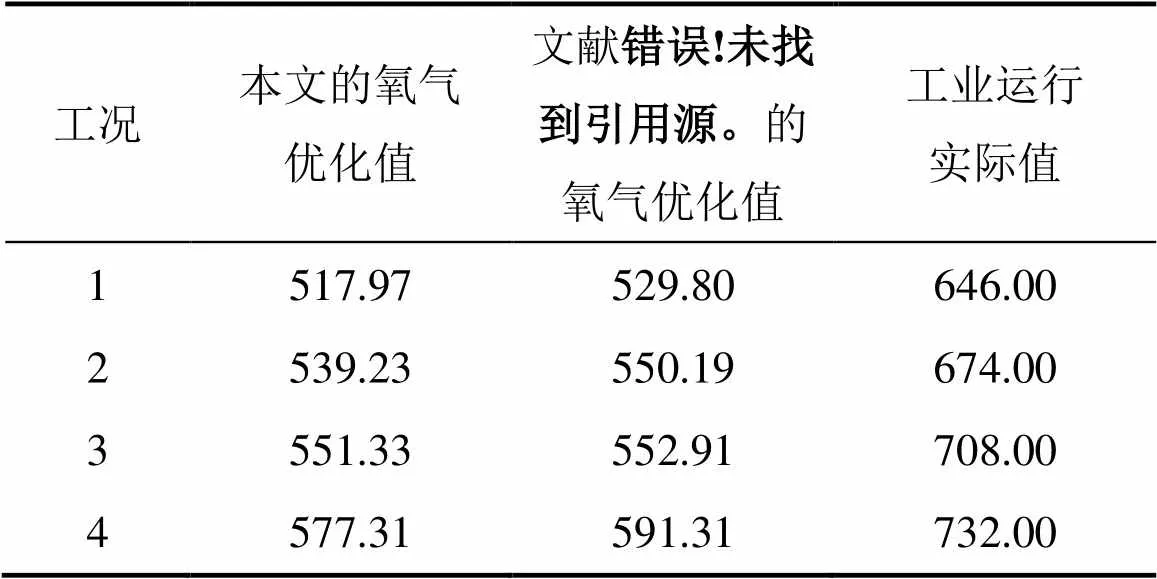
表6 氧氣消耗量比較

5 結(jié)論

1) 利用佳點(diǎn)集方法產(chǎn)生初始狼群個(gè)體，采用對數(shù)函數(shù)描述收斂因子以平衡灰狼算法的探索和開發(fā)能力，對當(dāng)前最好的3個(gè)灰狼個(gè)體執(zhí)行改進(jìn)的精英反向?qū)W習(xí)策略產(chǎn)生反向精英個(gè)體，以避免算法出現(xiàn)早熟 收斂。

2) 與其他群體智能優(yōu)化算法相比，改進(jìn)的GWO算法更具有競爭力。針鐵礦沉鐵工業(yè)過程參數(shù)優(yōu)化仿真結(jié)果表明，改進(jìn)的灰狼算法能適應(yīng)復(fù)雜工業(yè)過程的參數(shù)優(yōu)化。

[1] GAO W, LIU S, HUANG L. A novel artificial bee colony algorithm based on modified search equation and orthogonal learning[J]. IEEE Transactions on Cybernetics, 2013, 43(3): 1011?1024.

[2] DANESHYARI M, YEN G G. Constrained multiple-swarm particle swarm optimization within a cultural framework[J]. IEEE Transactions on Systems, Man, and Cybernetics: Part A, 2012, 42(2): 475?490.

[3] SURRY P D, RADCLIFFE N J. The COMOGA method: constrained optimization by multiobjective genetic algorithm[J]. Control and Cybernetics, 1997, 26(3): 391?412.

[4] SARKER R, ELSAYED S, RAY T. Differential evolution with dynamic parameters selection for optimization problems[J]. IEEE Trans Evol Comput, 2014, 18(5): 689?707.

[5] YANG Xinshe, DEB S. Cuckoo search via lévy flights[C]//Proceeding of World Congress on Nature and Biologically Inspired Computing. New York, American; IEEE Press, 2009: 210?214.

[6] YANG X S. Nature inspired meta-heuristic algorithms[M]. 2nd ed. Frome, UK: Luniver Press, 2010: 97?104.

[7] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(7): 46?61.

[8] 王鈦, 許斌, 李林國, 等. 基于離散灰狼算法的多級閾值圖像分割[J]. 計(jì)算機(jī)技術(shù)與發(fā)展, 2016, 26(7): 30?35. WANG Tai, XU Bin, LI Linguo, et al. A multi-threshold image segmentation algorithm based on discrete grey wolf optimization[J]. Computer Technology and Development, 2016, 26(7): 30?35.

[9] EL-FERGANY A, HASANIEN H. Single and multi-objective optimal power flow using grey wolf optimizer and differential evolution algorithms[J]. Electric Power Components and Systems, 2015, 43(13): 1548?1559.

[10] 陳金紅, 程剛. 灰狼優(yōu)化算法?投影尋蹤模型在云南省水量分配中的應(yīng)用[J]. 三峽大學(xué)學(xué)報(bào)(自然科學(xué)版), 2016, 17(3): 68?72. CHEN Jinhong, CHENG Gang. Application of grey wolf optimization algorithm?projection pursuit model to water allocation for Yunnan province[J]. Journal of China Three Gorges University (Natural Sciences), 2016, 17(3): 68?72.

[11] MOURA OLIVEIRA P B, FREIRE H, SOLTEIRO PIRES E J. Grey wolf optimization for PID controller design with prescribed robustness margins[J]. Soft Computing, 2016, 20(11): 4243?4255.

[12] 姚鵬, 王宏倫. 基于改進(jìn)流體擾動(dòng)算法與灰狼優(yōu)化的無人機(jī)三維航路規(guī)劃[J]. 控制與決策, 2016, 31(4): 701?708. YAO Peng, WANG Honglun. Three-dimensional path planning for UAV based on improved interfered fluid dynamical system and grey wolf optimizer[J]. Control and Decision, 2016, 31(4): 701?708.

[13] SAREMI S, MIRJALILI S Z, MIRJALILI S M. Evolutionary population dynamics and grey wolf optimizer[J]. Neural Computing and Applications, 2015, 26(5): 1257?1263.

[14] 龍文, 蔡紹洪, 焦建軍, 等. 求解高維優(yōu)化問題的混合灰狼優(yōu)化算法[J]. 控制與決策, 2016, 31(11): 1991?1997. LONG Wen, CAI Shaohong, JIAO Jianjun. Hybrid grey wolf optimization algorithm for high-dimensional optimization[J]. Control and Decision, 2016, 31(11): 1991?1997.

[15] 徐松金, 龍文. 嵌入遺傳算子的改進(jìn)灰狼優(yōu)化算法[J]. 蘭州理工大學(xué)學(xué)報(bào), 2016, 42(4): 102?108. XU Songjin, LONG Wen. Improved grey wolf optimization algorithm embedded with genetic operators[J]. Journal of Lanzhou University of Technology, 2016, 42(4): 102?108.

[16] 徐達(dá)宇, LIU Renping. 基于改進(jìn)自組織臨界優(yōu)化的元啟發(fā)式灰狼優(yōu)化算法[J]. 計(jì)算機(jī)應(yīng)用, 2016, 36(6): 1588?1593. XU Dayu, LIU Renping. Improved self-organized criticality optimized gray wolf optimizer metaheuristic algorithm[J]. Journal of Computer Applications, 2016, 36(6): 1588?1593.

[17] HAUPT R, HAUPT S. Practical genetic algorithm[M]. New York: John Wiley & Sons, 2004: 339?350.

[18] 張鈴, 張鈸. 佳點(diǎn)集遺傳算法[J]. 計(jì)算機(jī)學(xué)報(bào), 2001, 24(9): 917?922. ZHANG Ling, ZHANG Bo. Good point set based genetic algorithm[J]. Chinese Journal of Computers, 2001, 24(9): 917?922.

[19] 戴文樂, 楊新智. 基于慣性權(quán)重對數(shù)遞減的粒子群優(yōu)化算法[J]. 計(jì)算機(jī)工程與應(yīng)用, 2015, 51(17): 14?19. DAI Wenle, YANG Xinzhi. Particle swarm optimization algorithm based on inertia weight logarithmic decreasing[J]. Computer Engineering and Applications, 2015, 51(17): 14?19.

[20] ZHU Aijun, XU Chuangpei, LI Zhi, et al. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC[J]. Journal of Systems Engineering and Electronics, 2015, 26(2): 317?328.

[21] 熊富強(qiáng), 桂衛(wèi)華, 陽春華, 等. 一種雙種群協(xié)同進(jìn)化算法在濕法煉鋅過程中的應(yīng)用[J].控制與決策, 2013, 28(4): 590?594. XIONG Fuqiang, GUI Weihua, YANG Chunhua, et al. A double population co-evolution algorithm for process of zinc hydrometallurgy[J]. Control and Decision, 2013, 28(4): 590?594.

(編輯 楊幼平)

Improved grey wolf optimization algorithm with logarithm function describing convergence factor and its application

WU Tiebin1, 2, GUI Weihua1, YANG Chunhua1, LONG Wen3, LI Yonggang1, ZHU Hongqiu1

(1. School of Information Science and Engineering, Central South University, Changsha 410083, China; 2. College of Energy and Electrical Engineering, Hunan University of Humanities, Science and Technology, Loudi 417000, China; 3. Key Laboratory of Economics System Simulation, Guizhou University of Finance and Economics, Guiyang 550025, China)

The grey wolf optimization (GWO) algorithm has a few disadvantages such as low precision and high possibility of being trapped in local optimum, an improved GWO algorithm was proposed for solving high-dimensional optimization problem based on the convergence factor about logarithmic function. An initial population was generated based on good point set method to assure that the individuals were distributed in the search space as uniformly as possible. A nonlinear convergence factor was proposed based on logarithm function to balance the exploration ability and exploitation ability. Improved elite opposition-based learning strategy was used to avoid premature convergence of GWO algorithm. Benchmark functions and parameters optimization of real application were employed to verify the performance of the improved GWO algorithm. The results show that the proposed algorithm has better performance.

grey wolf optimization algorithm; logarithm function; convergence factor

TP273.1

A

1672?7207(2018)04?0857?08

10.11817/j.issn.1672?7207.2018.04.012

2017?04?29；

2017?06?22

國家自然科學(xué)基金資助項(xiàng)目(61621062，61463009，61673400)；湖南省自然科學(xué)基金青年基金資助項(xiàng)目(2016JJ3079)；貴州省科學(xué)技術(shù)基金資助項(xiàng)目(黔科合基礎(chǔ)[2016]1022)；婁底市科技計(jì)劃項(xiàng)目(2017)(Projects(61621062, 61463009, 61673400) supported by the National Natural Science Foundation of China; Project(2016JJ3079) supported by the Youth Fund of the Natural Science Foundation of Hunan Province; Project([2016]1022) supported by the Fund of Guizhou Science and Technology; Project(2017) supported by the Fund of Loudi Science and Technology)

龍文，博士，教授，從事系統(tǒng)建模與智能優(yōu)化研究；E-mail：lw227@mail.gufe.edu.cn