基于標準雙邊控制的改進力反饋遙操作方法

鄭義東，于勁松，唐荻音，陳小奇

基于標準雙邊控制的改進力反饋遙操作方法

鄭義東1，于勁松1，唐荻音1，陳小奇2

(1. 北京航空航天大學 自動化科學與電氣工程學院，北京，100191； 2. 坎特伯雷大學 工程學院，新西蘭 基督城，8042)

針對空間機器人遙操作過程中的通訊時延問題，提出一種改進的PD雙邊力反饋遙操作控制系統。首先從理論上推導該控制系統絕對穩定的條件。在保證系統穩定的前提下，進一步研究提高系統透明性的方法并給出控制參數的約束條件。通過與標準PD雙邊控制方法的對比實驗以及固定時延與變時延2種不同條件下的仿真實驗，驗證該改進方法具有顯著提高遙操作系統透明性和跟蹤性能的作用。研究結果表明：所推導的穩定性條件和透明性分析結論進一步完善了該PD雙邊控制方法，可對復雜遙操作系統中應用該方法提供參考。

遙操作系統；PD雙邊控制；力反饋；穩定性分析；透明性分析

隨著科技的進步與發展，人類的活動空間在不斷擴展，各國對遙操作空間機器人應用的重視程度逐年增加[1?2]。近年來，美國、日本等一些國家對大時延遙操作技術進行了大規模的研究和實驗，如歐洲航天局(ESA)研制了世界上第1個可從地面進行遙操作控制的空間機器人ROTEX[3?4]；日本前宇宙開發事業集團(NASDA)研制了第1個能實現艙外自由飛行的空間機器人ETS-VII[5]，它具有地面遙操作以及在軌自主控制的能力；美國國防部先進研究項目局(DARPA)研制了能夠自主完成在軌服務的Orbital Express機器人[6]；此外，還有我國于2013年底成功發射的“嫦娥三號”，將首個著陸器和“玉兔號”巡視器送抵月球，首次實現地外天體表面的無人自動巡視和月面就位科學探測。遙操作機器人能夠在遠距離或危險環境下執行未知或復雜任務，因此，在航空航天、深海勘探領域[7?8]，核輻射、高壓輸電、易燃易爆等危險領域以及醫療手術、建筑施工等領域均取得了廣泛應用[9?11]。遙操作系統的控制方法多種多樣：監督控制主要采取遙編程的方式對從機械臂進行控制[12]；基于事件的控制方法以與時間無關的參考變量(事件)代替時間作為信號的參考變量，能有效解決時延問題；線性二次最優控制理論將遙操作系統看成是一個具有狀態或輸出時延的反饋系統，通過設計相應的LQ控制器進行控制[13]；基于∞理論的控制方法可以將系統的擾動或者模型的不確定因素對系統的影響降低到期望的程度；基于滑模控制的方法可以保證基于互聯網通信的遙操作系統具有較好的魯棒性；基于虛擬現實的控制方法利用計算機圖形及相關技術，生成一種虛擬環境并給用戶提供逼真的視、聽、觸、力等多維感覺，是解決時延問題的重要手段[14]；PID控制方法根據被控制變量的實際輸出值與參考值之間的誤差來調節控制器的輸出，從而實現使被控制量的實際輸出跟蹤參考值。通訊時延問題是遙操作技術面臨的主要難點之一，也是研究的一個熱點方向[15?16]。目前，解決這一問題的主要方法有圖形預測仿真技術和雙邊力反饋技 術[17?19]。與圖形預測仿真技術相比，雙邊力反饋技術具有如下優勢：不要求遠端操作環境為結構化或已知的環境；在通信線路中傳送數據，降低了對通信帶寬的要求；把從手與環境的作用力直接作用于操作者，將人的智能直接加入控制回路，具有較高的可靠性和安全性[20]。目前，雙邊遙操作控制結構主要有3種：位置?位置型、力?位置型以及力反饋?位置型。與前2種控制結構相比，力反饋?位置型控制結構可以顯著提高遙操作系統力覺臨場感的效果，改善主?從遙操作機器人系統的動態特性，使系統透明性提高。但是，在大時延情況下，這些控制方法都很難保證遙操作系統的穩定性及透明性[21?22]。本文作者提出一種改進的PD雙邊控制方法。與其他雙邊力反饋控制方法相比，該方法簡單易行，便于設計，并且在保證系統穩定的前提下，能夠極大提高系統的透明性。在此基礎上，結合仿真實驗進行驗證，從而達到進一步完善PD雙邊控制方法的目的。

1 改進的PD雙邊控制方法

本文提出的PD雙邊控制方法是在標準二通道雙邊控制方法的基礎上改進優化得來的。標準PD雙邊控制結構是一種典型的力反饋?位置型控制結構，其原理如圖1所示。主從端分別用獨立的PD控制器進行控制，前向傳遞和反向反饋的分別是主從手的位置信息。圖中u和e分別為操作者施加的力和從手與環境的相互作用力；h和c分別為主從手的位置；1和2分別為由主端到從端的時延和由從端到主端的時延。

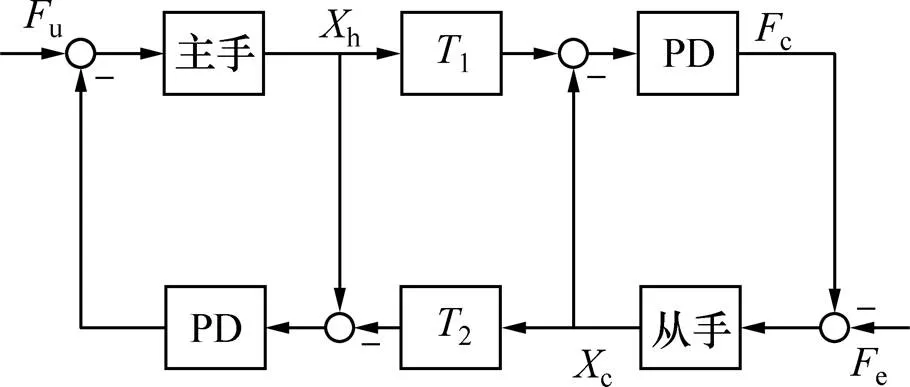
圖1 標準PD雙邊控制原理圖

實驗表明，當時延在2 s以上時，采用標準PD雙邊控制的遙操作系統雖然能夠保持穩定，但是它的透明性卻并不理想。在此基礎上本文提出了一種改進的PD雙邊方法。

改進的PD控制器模型為

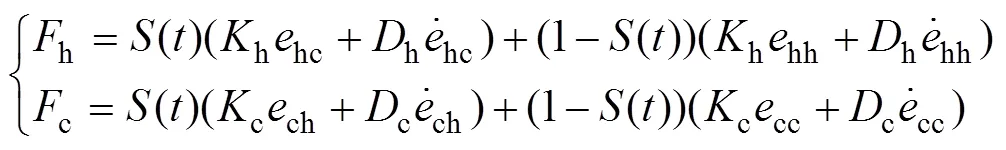
式中：h和c分別為主端控制器和從端控制器的比例系數；h和c分別為主端控制器和從端控制器的微分系數。式(1)中的各項位置誤差定義如下：

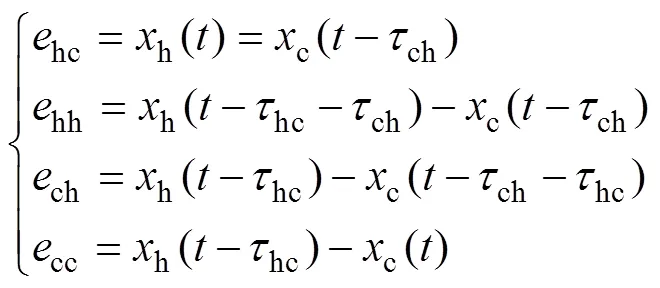
式中：hh和cc分別為信息在主端和從端之間傳輸的往返時延；hc和ch分別為信息由主端到從端和由從端到主端傳輸的單向時延。

當主手受到操作者的控制而向前運動時，會在從手坐標系中產生相對誤差cc，從手控制器會根據式(1)產生力c驅動從手運動。另一方面，從手將此誤差cc傳遞給主端，反饋回主端的位置誤差為hh，主端控制器根據此誤差產生力h來感受從端的控制力，從而產生了臨場感，提高了控制系統的透明性。

式(1)中的函數()的取值被限定為0或1，它的作用是決定使用哪一個控制器來進行反饋，其計算公式如下：

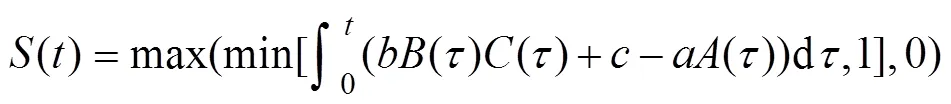
其中：

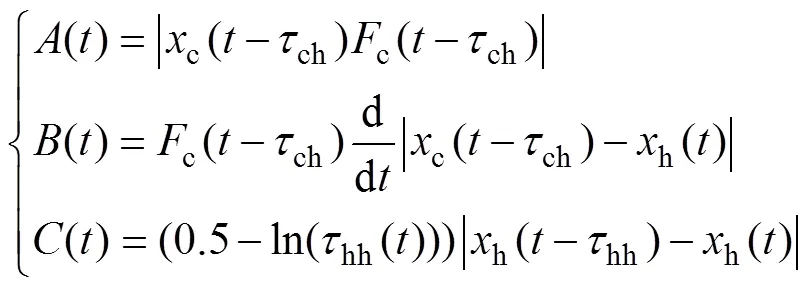
式(3)中，增益和反映了控制器拾取外力的敏感度。越大，控制器透明性就越好；越大，控制器對外力就越敏感。常數的作用是當控制器未激活時將系統逐漸變為完全透明的雙邊遙操作系統。

當從手產生位移并從系統中帶走能量時，函數()的存在使得()減小，進而使得系統無源。主從端位置誤差的產生主要有2個原因：一是當主手運動時，從手還未到達相應位置，二是當從端有障礙存在時，在障礙處從手會停止運動。函數()的作用便是通過微分函數來辨別這2種情況。函數()的主要作用是通過觀測主手在傳輸時延內的運動量從而將時延因素考慮進去。例如，在大時延存在的情況下，當主手迅速移動時，會有1個顯著的力反饋給主端操作者，函數()可以通過預測此位移量來減小反饋力，以此來保持系統的穩定性。

2 方法的穩定性分析

遙操作系統的性能主要包括穩定性和透明性2個方面。穩定性是控制系統發揮作用的基本前提，是所有的控制系統必須滿足的條件。系統穩定可以簡單地理解為包括操作者和從端環境在內的整個控制系統的狀態變量始終有界。本節就改進PD雙邊控制系統的穩定性進行分析，并推導出控制系統的絕對穩定性 條件。

2.1 穩定性判據

常用的穩定性判據有無源性判據和絕對穩定性判據，理論上可以證明無源穩定性是絕對穩定性的充分不必要條件[23]，因此絕對穩定性判據可以降低系統的保守性，應用更加廣泛。Llewellyn絕對穩定判據是其中較為常見的一種[24]。

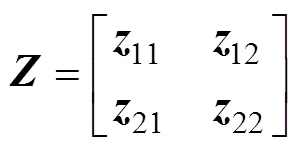
2.2 穩定性分析

函數()的取值被限定為0或1，下面分別對()取不同值時的控制系統進行分析。

當()=1時，遙操作系統的二端口網絡模型為

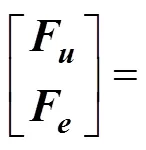
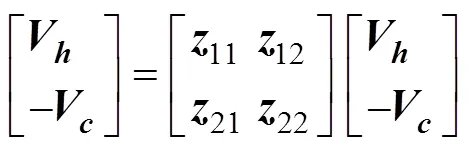
根據Llewellyn準則，可以推導出系統絕對穩定的條件：

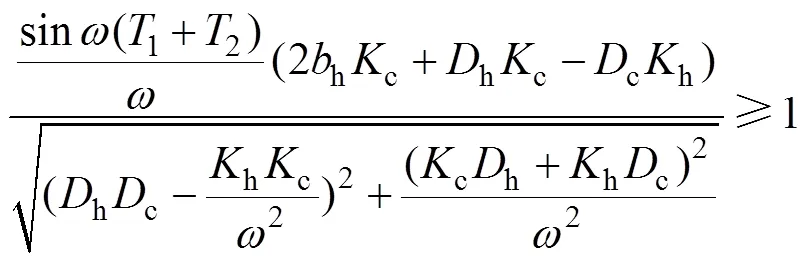
從圖2可以看出：對于固定的c和c，1是有界的，因此，只要選擇的c和c合適，不等式(7)總是可以滿足的。

圖2 y1關于頻率ω的變化曲線

式(8)可以表示為

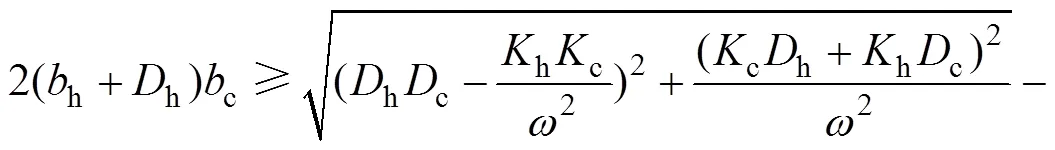
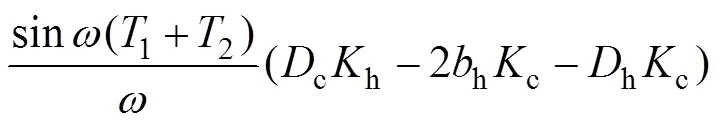
令

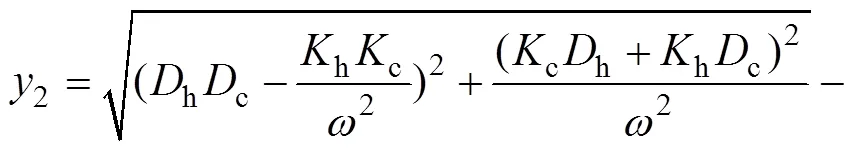
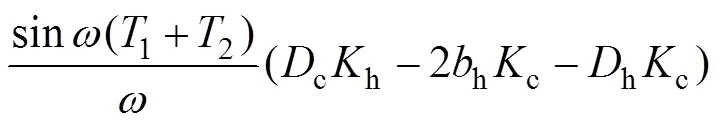
設c=h=1，1=2=3 s，c=h=0.5，h=1，可以得到2關于頻率的變化情況，如圖3所示。

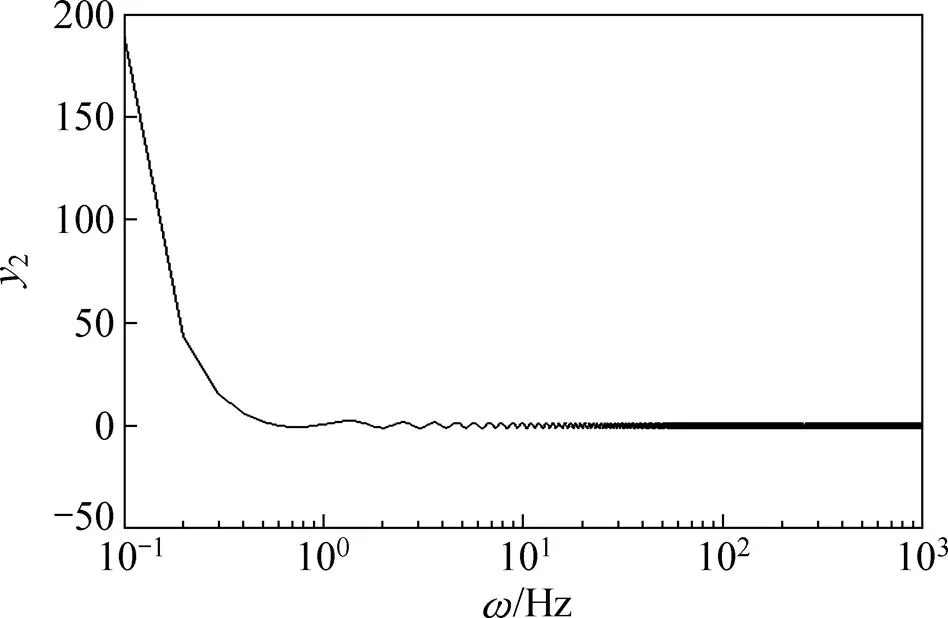
圖3 y2關于ω的變化曲線

當c，h，c和h固定時，函數2的取值在整個頻率范圍內是有界的，因此，只要選擇合適的參數c，h，c和h，就可使得不等式(9)得到滿足。

當() =0時，遙操作系統的二端口網絡模型為

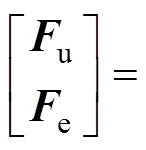
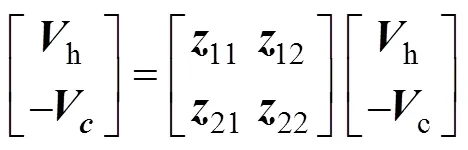
式中：h和c分別為主手和從手的質量；h和c分別為主手和從手的阻尼。

根據Llewellyn準則，可以推導出系統絕對穩定的條件為：

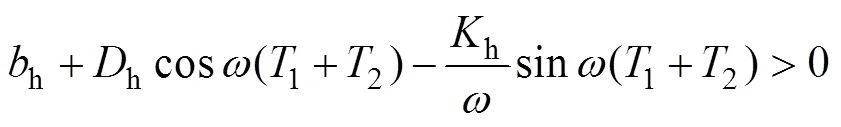
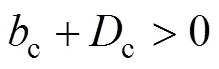
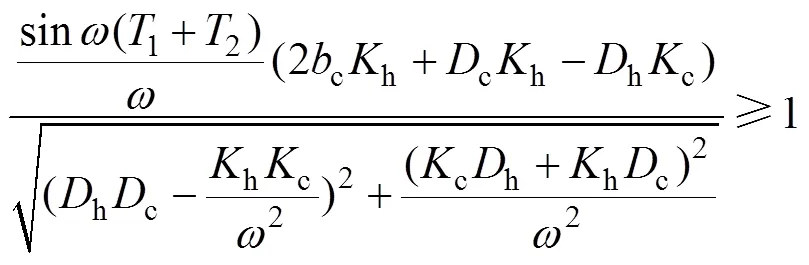
同理，只要選擇合適的參數c，h，c和h，就可使得上述不等式(12)，(13)和(14)成立，從而保證遙操作系統的絕對穩定。

3 方法的透明性分析

透明性是評價遙操作系統性能的另一重要指標。雙邊力反饋控制系統中，從端將其與環境相互作用的力信息反饋給主端，操作者便可以根據此反饋力感受到從端環境的狀態，這就是遙操作系統的臨場感。系統的透明性是用來衡量系統臨場感質量的，透明性越好，系統的臨場感就越好。通常用主端操作者感受到的阻抗和環境阻抗之間的關系來衡量。定義操作者感受到的阻抗為h=h/h，環境的實際阻抗為e=e/c，因此，可以用h和e之間的相似程度來衡量透明性。它們的相似度越高，系統的透明性越好，在理想情況下有h=e。本節從透明性方面對改進PD雙邊控制系統進行分析，并與前文穩定性條件進行對比，推導出在保證穩定性的前提下使系統獲得最佳透明性的參數條件。

當()=1時，系統主從手運動學模型及PD控制模型為

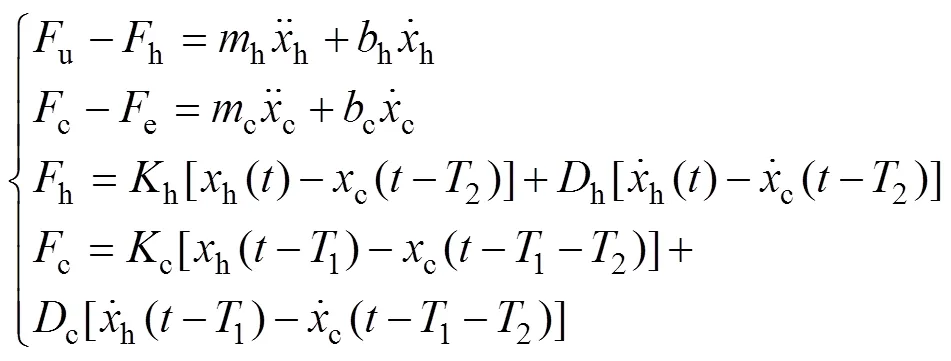
此時的主端阻抗為

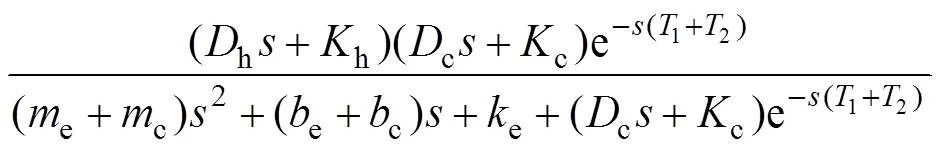
通過冪級數展開將其化為如下形式：

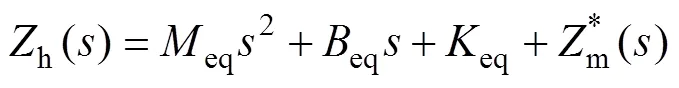
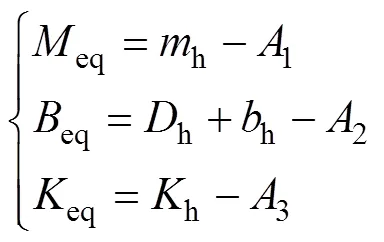
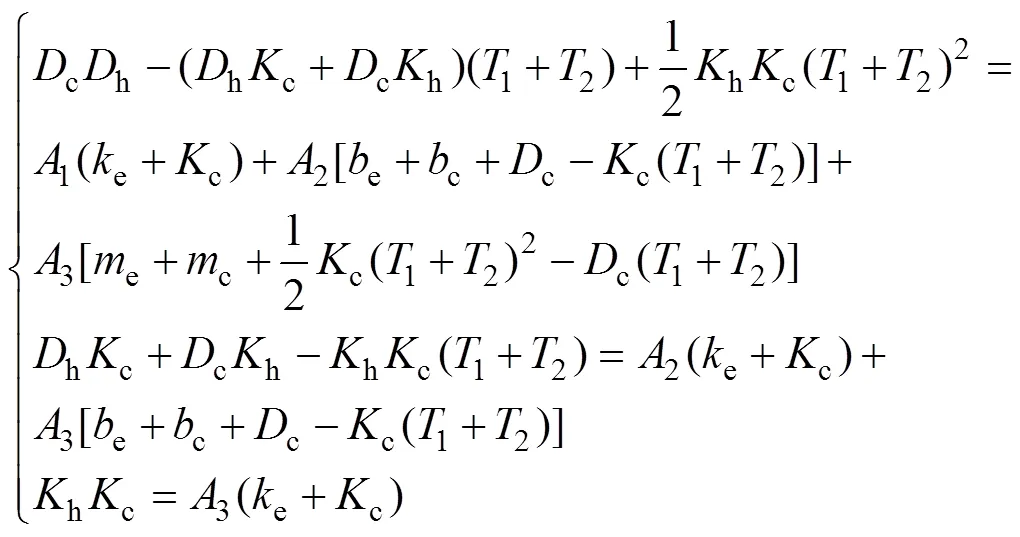
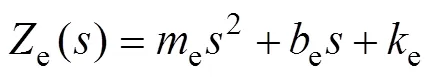
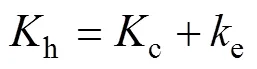
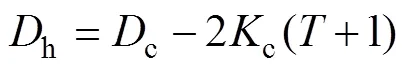
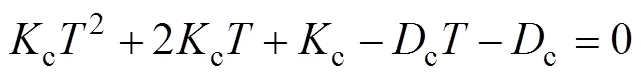
為簡化計算，假設信息在主從端傳遞的單向時延相等，即1=2=。不失一般性，將主從端及環境模型的各參數設為：h=c=e=0.5 kg，h=c=e=0.5 kg/s，e=0.5 N/m。其中和分別表示質量和阻尼；為彈性系數。將式(20)，(21)和(22)與系統穩定條件(6)，(7)和(8)聯立，以c，c和為自變量利用MATLAB畫出其三維空間圖。

由圖4可見：透明性最優約束與系統穩定域是有交集的，說明可以在該穩定域內找到使系統透明性最佳的參數取值。當() =0時，可以相同的方法得到最佳參數取值的約束條件。

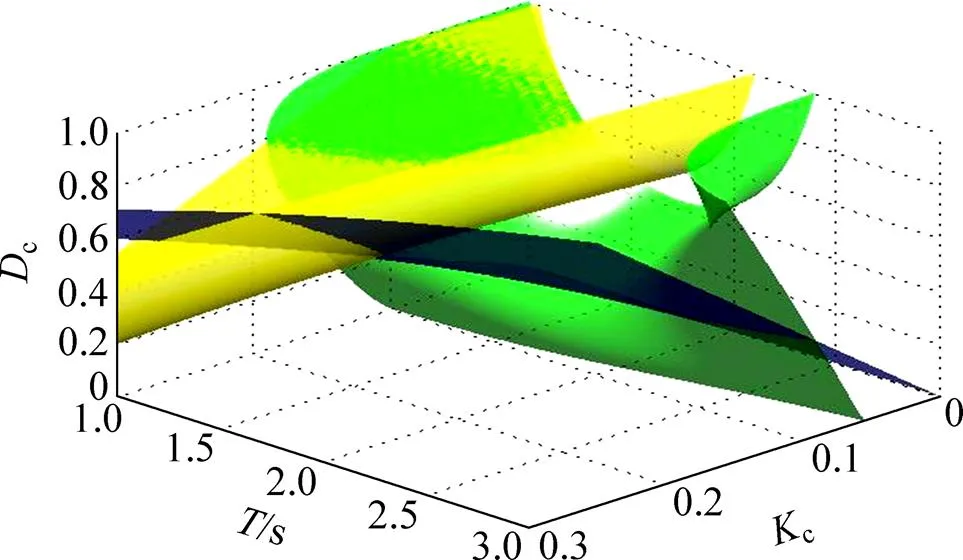
圖4 系統穩定性與透明性的參數約束關系

4 仿真實驗

為了更直觀地表現改進PD雙邊控制方法的控制效果以及驗證前兩節理論推導結果的正確性，本節對大時延下采用改進PD雙邊控制方法控制的遙操作系統進行仿真。由于在實際工程中，時延并不是一個固定不變的常數，而是隨著時間動態變化的，因此，本節除了固定時延的情況外，還將對變時延情況下的遙操作系統進行仿真。

4.1 固定時延仿真結果

利用simulink工具對改進PD雙邊控制系統進行仿真。其中，主從手的質量和阻尼分別設置為h=0.5 kg，h=0.2 kg/s，c=0.5 kg，c=0.2 kg/s。為簡單起見，將環境模型設為二階質量?彈簧?阻尼系統：

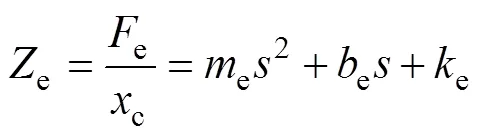
其中：e=0.05 kg，e=0.025 kg/s，e=0.125 N/m。系統單邊時延設為1=2=2 s。

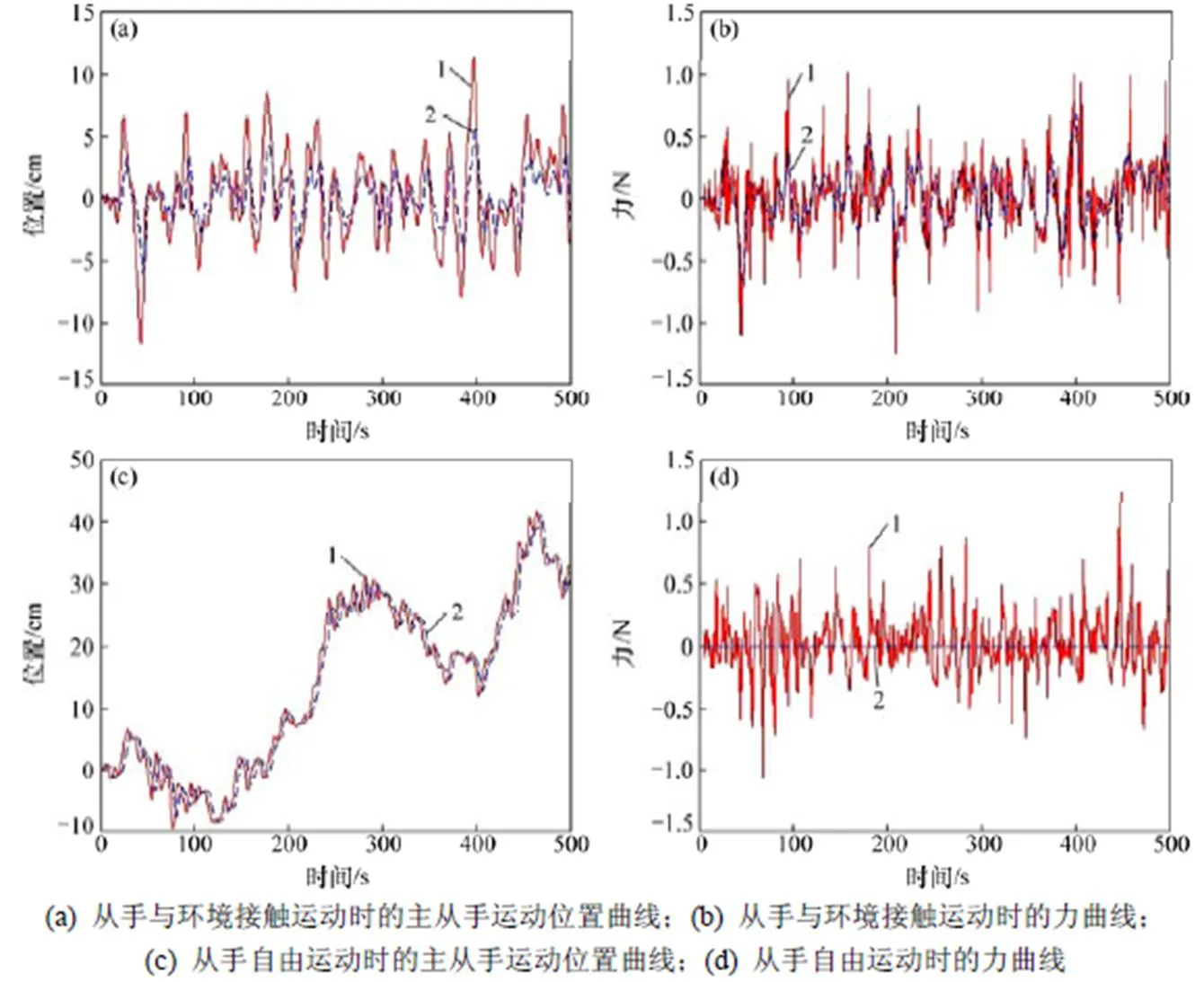
仿真結果如圖5所示。圖5(a)和(b)所示分別為從手與環境接觸運動時主從手的運動位置曲線和力曲線，圖5(c)和(d)所示分別為從手自由運動時主從手的運動位置曲線和力曲線。從圖5(a)和(c)可以看出：無論從手是自由運動還是與環境接觸運動，主從手的運動位置曲線均是有界的，并未發生振蕩發散現象，這表明遙操作系統是穩定的，而主從手運動位置曲線的擬合程度則表征著系統的跟蹤性能。當從手基本能夠跟蹤主手進行位移運動時，可近似用主端感受到的反饋力h和從端與環境之間的作用力e來衡量系統的透明性。從圖5(b)可以看出：h與e十分接近，相似度極高，系統的臨場感非常好。當從手自由運動時，從圖5(d)可以看出主端感受力h并不雜亂，這也表明了系統的透明性較好。可見，當按照上文推出的參數約束條件選取控制參數時，改進PD雙邊控制方法的控制效果比較理想。

圖6所示為標準PD雙邊控制與改進PD雙邊控制方法的透明性對比。從圖6可以看出：圖6(b)中主從端阻抗的擬合度更好，這表明改進的PD雙邊控制系統的透明性更好，優于標準PD雙邊控制系統。

4.2 變時延仿真結果

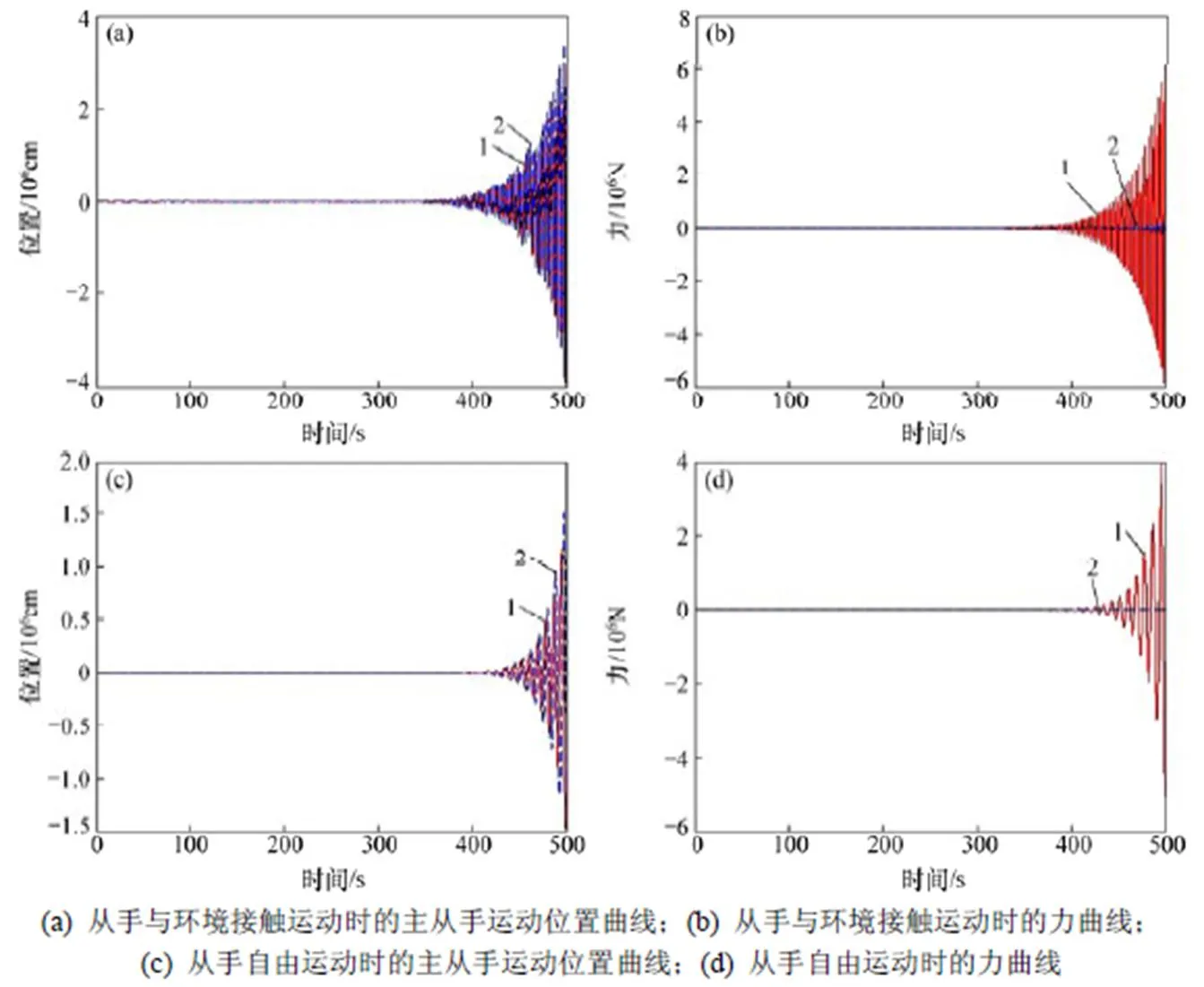
為了驗證前文推導的穩定性與透明性條件對于一些復雜情況下系統控制參數的選取是否適用，在以上實驗基礎上，將固定時延改為在1.5~2.5 s之間隨機變化的時變時延，圖7所示為其仿真結果。

從圖7可以看到：在變時延情況下，系統的穩定性依舊能夠得到保證；透明性雖然有所下降，但仍然保持在較高的水平。

為驗證系統控制參數對遙操作系統性能的影響，本文進行了另一組控制參數不滿足穩定條件時的仿真實驗，仿真結果如圖8所示。

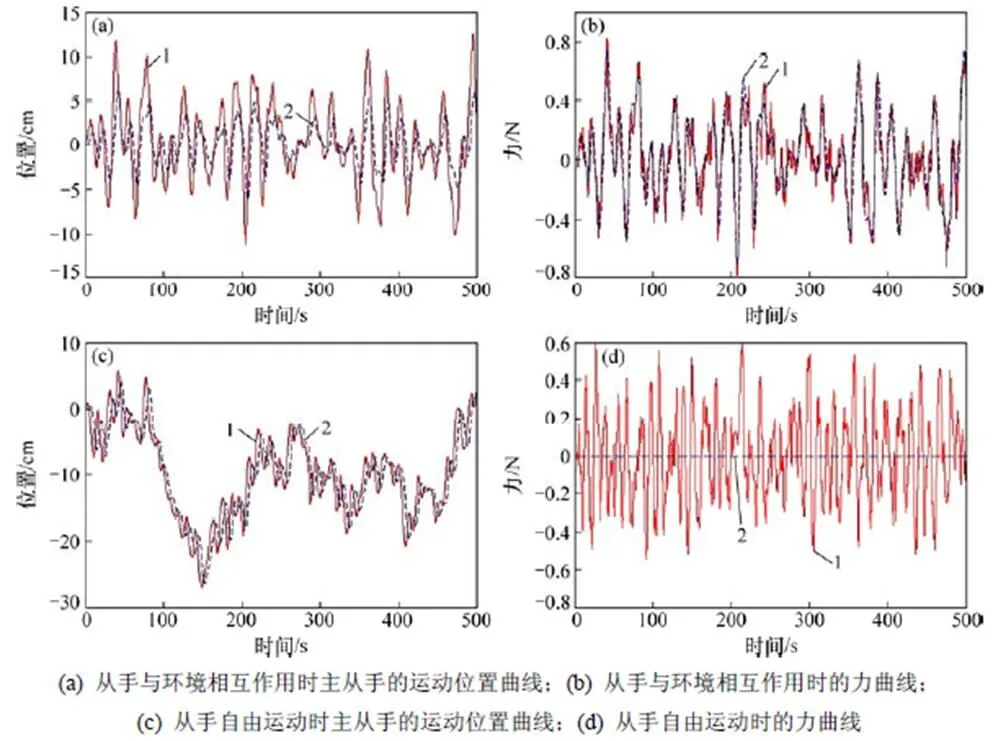
1—主手；2—從手。

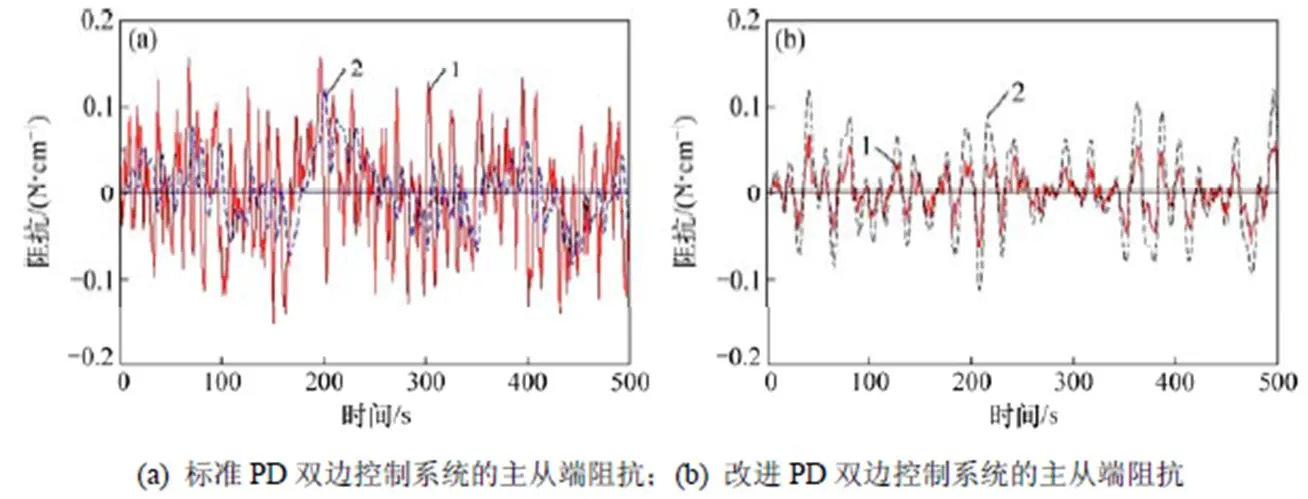
1—主端阻抗；2—從端阻抗。

1—主手；2—從手。

1—主手；2—從手。

由圖8可見：主從手的運動位置曲線隨著仿真時間的推進出現了振蕩發散現象，說明此時系統是極其不穩定的，從而驗證了系統穩定性分析結果的正確性。

4.3 跟蹤性能對比仿真結果

圖9和圖10所示分別為標準PD控制方法和改進PD控制方法在相同條件下主從手的運動情況對比。

雙邊控制系統的跟蹤性定義為從手跟蹤1時刻前主手運動的精度(其中1表示由主端到從端的時延)，在仿真曲線上則表現為從手位置跟蹤主手位置的誤差，誤差越小，則系統的跟蹤性能越好。

從圖9和圖10可以看出：無論從手處于自由運動還是與環境接觸運動，改進PD控制方法下從手跟蹤主手運動的能力均比標準PD控制方法時的好，說明改進PD控制方法的系統跟蹤性能相比于標準PD控制得到提高。

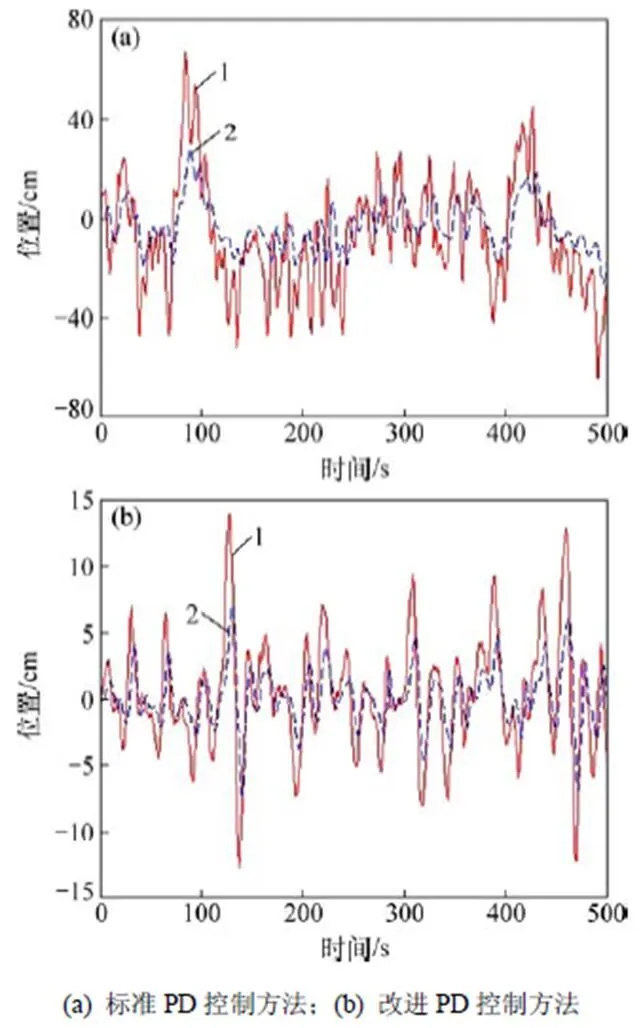
1—主手；2—從手。

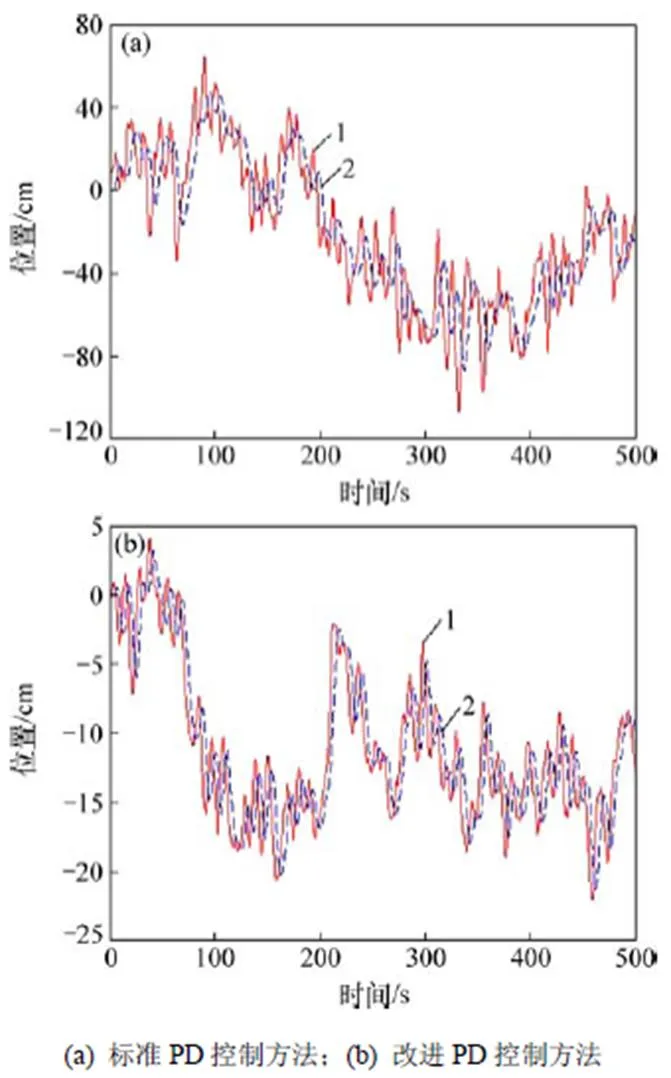
1—主手；2—從手。

5 結論

1) 根據Llewellyn絕對穩定判據推導出系統絕對穩定的條件，在此基礎上根據系統透明性定義推導出了在保證穩定的前提下，系統獲得最佳透明性應滿足的條件。

2) 仿真實驗驗證了推導的參數約束方程的正確性。改進的PD雙邊控制方法對于固定時延和時變時延均具有很好的適應性，能夠在保證遙操作系統穩定的同時使得系統的透明性顯著提高。

3) 改進的PD雙邊控制方法相比于標準PD控制方法能夠使遙操作系統的跟蹤性能進一步提高。

[1] MERSHA A Y, STRAMIGIOLI S, CARLONI R. On bilateral teleoperation of aerial robots[J]. IEEE Transactions on Robotics, 2014, 30(1): 258?274.

[2] REBELO J, SEDNAOUI T, DEN EXTER E B, et al. Bilateral robot teleoperation: A wearable arm exoskeleton featuring an intuitive user interface[J]. IEEE Robotics & Automation Magazine, 2014, 4(21): 62?69.

[3] BRUNNER B, HIRZINGER G, LANDZETTEL K, et al. Multisensory shared autonomy and tele-sensor- programming-key issues in the space robot technology experiment ROTEX[C]//Proceedings of the 1993 IEEE/RSJ International Conference on Intelligent Robots and Systems. New York: IEEE, 1993: 2123?2139.

[4] HIRZINGER G, BRUNNER B, DIETRICH J, et al. Sensor-based space robotics-ROTEX and its telerobotic features[J]. IEEE Transaction on Robotics and Automation, 1993, 9(5): 649?663.

[5] IMAIDA T, YOKOKOHJI Y, DOI T, et al. Ground-space bilateral teleoperation of ETS-VII robot arm by direct bilateral coupling under 7s time delay condition[J]. IEEE Transactions on Robotics and Automation, 2004, 20(3): 499?511.

[6] 劉進軍. 軌道快車—衛星拯救者[J]. 衛星電視與寬帶多媒體, 2007, 21(4): 40?42. LIU Jinjun. Orbital express-the savior of satellites[J]. Satellite TV & IP Multimedia, 2007, 21(4): 40?42.

[7] VOZAR S, LEONARD S, KAZANZIDES P, et al. Experimental evaluation of force control for virtual-fixture-assisted teleoperation for on-orbit manipulation of satellite thermal blanket insulation[C]//2015 IEEE International Conference on Robotics and Automation(ICRA). Seattle: IEEE, 2015: 4424?4431.

[8] WILDE M, CHUA Z K, FLEISCHNER A. Effects of multivantage point systems on the teleoperation of spacecraft docking[J]. IEEE Transactions on Human-Machine Systems, 2014, 44(2): 200?210.

[9] MUKHERJEE J K. Fast visualization technique for view constrained teleoperation in nuclear industry[C]//2014 International Conference on Information Science and Applications(ICISA). Seoal: IEEE, 2014: 1?4.

[10] NISKY I, HSIEH M H, OKAMURA A M. Uncontrolled manifold analysis of arm joint angle variability during robotic teleoperation and freehand movement of surgeons and novices[J]. IEEE Transactions on Biomedical Engineering, 2014, 61(12): 2869?2881.

[11] PACCHIEROTTI C, ABAYAZID M, MISRA S, et al. Teleoperation of steerable flexible needles by combining kinesthetic and vibratory feedback[J]. IEEE Transactions on Haptics, 2014, 7(4): 551?556.

[12] AI-MOUHAMED M, NAZEERUDDIN M, MERAH N. Design and instrumentation of force feedback in telerobotics[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(6): 1949?1957.

[13] BACOCCO R, MELCHIORRI C. LQ control design of cooperative teleoperation system[C]//Proceedings 2009 14th International Conference on Advanced Robotics. Tokyo: IEEE, 2009: 490?495.

[14] 胡凌燕. 時延力反饋遙操作系統的跟蹤性能及穩定性研究[D]. 江西: 南昌大學機電工程學院, 2011: 4?9. HU Lingyan. Trajectory tracking and stability of teleoperator with time delay and force feedback[D]. Jiangxi: Nanchang University. School of Mechanical and Electrical Engineering, 2011: 4?9.

[15] 陳俊杰. 空間機器人遙操作克服時延影響的研究進展[J]. 測控技術, 2007, 26(2): 1?5. CHEN Junjie. Research headway of overcoming time-delay infection for teleoperation of space robot[J]. Measurement and Control Technology, 2007, 26(2): 1?5.

[16] NIEMEYER G, SLOTINE J E. Telemanipulation with time delays[J]. The International Journal of Robotics Research, 2004, 23(9): 873?890.

[17] 賈慶軒, 高欣, 孫漢旭, 等. 面向機器人遙操作的預測圖形仿真技術[J]. 航空制造技術, 2011(7): 60?63. JIA Qingxuan, GAO Xin, SUN Hanxu, et al. Predictive graphical simulation technology for robot teleoperation[J]. Aeronautical Manufacturing Technology, 2011(7): 60?63.

[18] 王學謙, 梁斌, 李成, 等. 自由飛行空間機器人遙操作三維仿真系統研究[J]. 宇航學報, 2009, 30(1): 402?408. WANG Xueqian, LIANG Bin, LI Cheng, et al. Study on three dimensional predictive simulation system of teleoperation for free flying space robot[J]. Journal of Astronautics, 2009, 30(1): 402?408.

[19] 鄧啟文, 韋慶, 李澤湘. 大時延力反饋雙邊控制系統[J]. 機器人, 2005, 27(5): 410?413. DENG Qiwen, WEI Qing, LI Zexiang. Force-reflection bilateral control system with large time delay[J]. Robot, 2005, 27(5): 410?413.

[20] 張濤, 陳章, 王學謙, 等. 空間機器人遙操作關鍵技術綜述與展望[J]. 空間控制技術與應用, 2014, 40(6): 1?9. ZHANG Tao, CHEN Zhang, WANG Xueqian, et al. Overview and prospect of key technologies of teleoperation of space robot[J]. Aerospace Control and Application, 2014, 40(6): 1?9.

[21] 鄧啟文, 韋慶, 李澤湘. 力反饋時延遙操作系統的時延相關穩定性分析[J]. 控制理論與應用, 2007, 24(5): 815?818. DENG Qiwen, WEI Qing, LI Zexiang. Analysis of delay-dependent stability for time-delay teleoperating systems with force-reflection[J]. Control Theory and Applications, 2007, 24(5): 815?818.

[22] DENG Qiwen, WEI Qing, LI Zexiang. Improving the transparency of teleoperating system[C]//Proceedings of the 25thChinese Control Conference. Harbin: IEEE Press, 2006: 861?866.

[23] 李寬. 基于絕對穩定性的空間機器人遙操作算法研究[D]. 湖南: 國防科學技術大學控制科學與工程學院, 2007: 21?22. LI Kuan. Research on control algorithms of space robot teleoperation based on the absolute stability[D]. Hunan: National University of Defense Technology. School of Control Science and Control Engineering, 2007: 21?22.

[24] 劉威, 宋愛國. 基于虛擬現實的力覺臨場感系統及其穩定性分析[J]. 儀器儀表學報, 2006, 27(z2): 1090?1093. LIU Wei, SONG Aiguo. Force-reflecting teleoperation system based on virtual reality and its stability analyse[J]. Chinese Journal of Scientific Instrument, 2006, 27(z2): 1090?1093.

(編輯 楊幼平)

An improved force feedback method for teleoperation control system based on standard PD bilateral control

ZHENG Yidong1, YU Jinsong1, TANG Diyin1, CHEN Xiaoqi2

(1. School of Automation and Electrical Engineering, Beihang University, Beijing 100191, China; 2. College of Engineering, University of Canterbury, ChristChurch8042, New Zealand)

In order to handle communication time delay problem in space robot teleoperation, an improved proportion and differentiation (PD) bilateral force feedback method for teleoperation control system was proposed. The absolute stability condition was theoretically deduced at first. On the premise of stable conditions, the transparency was further studied and the constraint conditions of control parameters that guarantee the best transparency were derived. Two simulation experiments were conducted to verify the significant effect of the proposed method that improved the teleoperation system’s transparency and tracking performance. One was a comparison experiment between standard PD bilateral control method and the improved PD bilateral control method, and the other was performance analysis of stability and transparency during fixed time delay and variable time delay. The derived stability and transparency conditions were supported by the simulation results. They are able to improve the PD bilateral force feedback control method and provide reference to its application in complex teleoperation systems.

teleoperation technology; PD bilateral control; force feedback; stability analysis; transparency analysis

V412；TP242

A

1672?7207(2018)04?0865?09

10.11817/j.issn.1672?7207.2018.04.013

2017?05?15；

2017?07?16

國家自然科學基金資助項目(71701008)(Project(71701008) supported by the National Natural Science Foundation of China)

于勁松，博士，副教授，從事虛擬儀器及自動測試系統、智能診斷技術、預測與健康管理技術研究；E-mail：yujs@buaa.edu.cn