繩、桿牽連模型中的加速度關系剖析
李志強
(濟寧市任城區教育體育局教研中心 山東 濟寧 272000)
繩、桿牽連模型是高中物理中常見力學模型,也是高考、自主招生和物理競賽的熱點.解決這類問題的關鍵,是要搞清用繩或桿相連的兩物體的運動關系.高中物理中一般地只涉及到兩物體的速度關系,對此人們已總結出了一些可行的方法.一種簡單且易接受的方法是,利用繩或桿不可伸縮的特點,根據兩物體在繩或桿長方向的速度分量相等,建立起兩物體間的速度關系.但加速度關系就不是那么簡單了.這里就此問題略作探討,希望對讀者能有所幫助.
下面用一個實例來具體說明.
如圖1所示,長為L的均勻直桿兩端固定著兩個小球A和B,A球在豎直墻壁上運動,B球在水平地面上運動.當桿與豎直墻壁的夾角為α,B球向右的速度為vB時,A球的速度和加速度分別為多少?
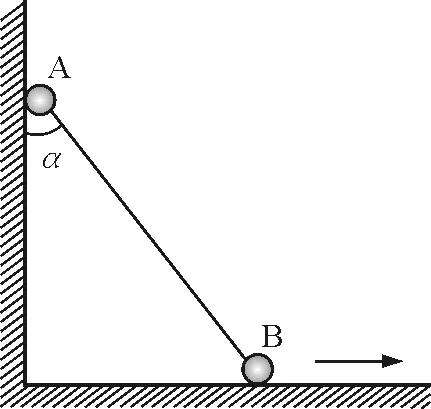
圖1 題圖
解析:如圖2所示,B球速度沿桿長方向的分量為

vA=vBtanα

圖2 A球、B球速度分解
假如B球有向右的加速度aB,那么A球的加速度為多少呢?
不少人認為:因繩、桿不可伸長,當其受到彈力作用時,繩和桿上各點的加速度在繩和桿方向上的投影相等.故常常這樣得出A球的加速度.
將B球的加速度沿桿方向投影,則
設A球的實際加速度為aA,其方向豎直向下,將它沿桿方向投影,則有
考慮到沿桿方向的加速度大小相等,所以
aBcos(90°-α)=aAcosα
解得
aA=aBtanα
其實上述兩球的加速度關系是錯誤的.正確的分析思路如下.
以B球為參考系,桿做逆時針轉動,A球的速度是B球的速度vB與A球隨桿轉動速度的矢量和,如圖3所示.由矢量關系得到
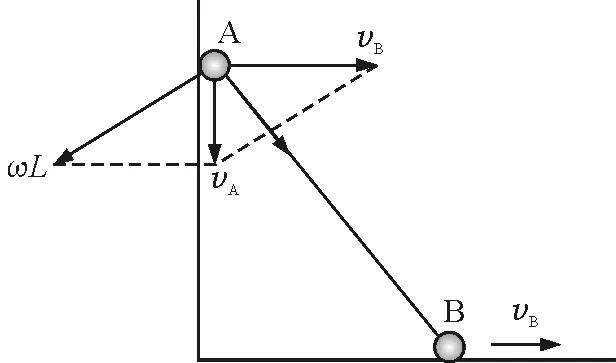
圖3 以B球為參考系
A球的運動可以看作是B球平動與繞B球逆時針轉動的合運動.B球有向右運動的加速度aB,它沿桿長方向的加速度分量
那么A球也具有這個加速度分量
另外由于轉動,A球還有沿桿的加速度分量
A球實際加速度aA豎直向下,所以有

通過討論我們認為:繩、桿牽連模型中的加速度關系超出了高中物理課本的知識范圍(但不超出高中學生的智力范圍,不超出高中物理競賽要求的能力范圍),一般地不要求學生掌握.但作為教師應正確理解繩、桿牽連模型中的加速度關系,以免“以其昏昏,使人昭昭”,把錯誤傳給學生,謬論流傳,誤人子弟.
參 考 文 獻
1 舒幼生.物理學難題集萃(增訂本).北京:高等教育出版社,1999.1 108~1 111
2 周衍柏.理論力學教程(第2版).北京:高等教育出版社,1986
3 王春勝.繩桿兩端物體速度的幾種處理方法.物理通報,2015(4):56~57

