肥皂水超疏水特性研究*
馮艦銳 張梓欽 吳秀文 董愛國 郝會穎
[中國地質大學(北京)數理學院 北京 100083]
1 引言
超疏水材料的基礎原理蓮花效應是20世紀70年代由波恩大學的植物學家巴特洛特在研究植物葉子表面時發現的,即蓮花表面因具有粗糙的微納米結構而產生的超疏水性,滴落在蓮葉表面的水滴與蓮葉形成的接觸角大于150°,于是液滴會因為表面張力的作用形成類似于球體的水珠. 自超疏水材料的誕生以來,人們已經將其應用到電子產業,醫療衛生,建筑業等各種領域.近年來,超疏水材料在防污、防腐和防凍等方面的應用使該類材料的研究成為國內外研究的熱點問題之一[1].
常見的超疏水材料通常都是固體材料[1,2],但是在特殊條件下,某些液體也可以具有超疏水特點. 例如,粘稠的液體在豎直振動時,其表面表現出超疏水特點,使其同成分液滴能夠在液體表面停留很長時間[3]. 目前,基于該方面的超疏水機理的研究已有幾十年,但基于液體表面在振動條件下的超疏水性能的實驗研究并不多[4].
本研究以肥皂水為例,以揚聲器為振源,從實驗角度對肥皂水表面在振動狀態下的超疏水性能進行了較為詳細的研究,并對實驗現象進行了分析.
2 實驗部分
本實驗裝置包括SG1646A信號發生器,揚聲器(振源),培養皿,肥皂水.
具體實驗過程為:配置不同濃度的肥皂水,并取20 ml移入培養皿中.調節信號發生器,記錄所示頻率,測量并記錄肥皂水的表面張力.而后,用針管汲取同濃度肥皂水并滴入至培養皿中的肥皂水表面,觀察并記錄液滴在液面上所形成的穩定水珠最大停留時間.本研究對處于振動狀態的肥皂水超疏水性質是通過其上所形成的穩定水珠最大停留時間來評價.
表面張力系數的測量采用扭秤測量法[5],如圖1所示.

圖1 扭秤
用游標卡尺測量П型絲的長度L,升高托盤,將П型絲浸入水中,轉動旋鈕將水膜拉起,在水膜即將被拉斷的瞬間記下h和β,重復該過程8~10次,取平均值. 通過對數據的擬合,得到表面張力與β的關系
F(β)=0.617β-27.76
(1)
3 結果與討論
3.1 肥皂水濃度對其臨界超疏水振動頻率的影響
圖2給出在肥皂水表面能夠形成穩定水珠所需的最小振動頻率與肥皂水濃度關系曲線.由圖2(a)可見,當肥皂水濃度由0.025 mol/L增加到0.25 mol/L時,形成穩定水珠所需的最小振動頻率約在30.7~31.6 Hz范圍內變化,但未發現明顯的變化規律;而當肥皂水濃度由0.0增加到0.025 mol/L時,形成穩定水珠所需的最小振動頻率由38.0 Hz下降至30.8 Hz,并且在低濃度(0.0~0.005 mol/L)情況下隨肥皂水濃度增加,在其表面形成穩定水珠所需最小振動頻率急劇下降,而當肥皂水濃度高于0.005 mol/L后,在其表面形成穩定水珠所需最小振動頻率變化趨于平緩.

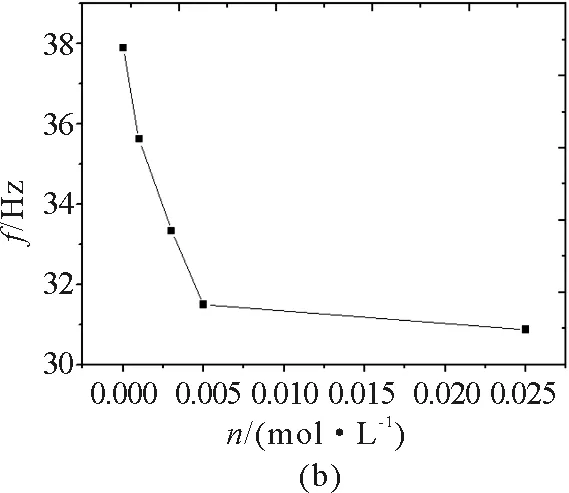
圖2 產生穩定水珠的最小振動頻率與肥皂水濃度關系曲線
3.2 振動頻率對肥皂水表面超疏水規律的影響
圖3是在肥皂水表面穩定水珠最大停留時間對振動頻率關系曲線. 該過程肥皂水濃度為0.03 mol/L. 在振動頻率f≤60 Hz時,在肥皂水表面穩定水珠最大停留時間很短,且隨著振動頻率的增大沒有明顯變化;但當振動頻率由60 Hz增加至85 Hz時,在肥皂水表面穩定水珠最大停留時間由5 s激增至84 s.

圖3 穩定水珠最大停留時間對振動頻率關系曲線
為了進一步研究產生該現象的原因,測量了肥皂水表面張力系數隨振動頻率的變化規律(圖4). 當振動頻率從零增加到50 Hz時,表面張力系數從147.6 N/m增加到227.2 N/m. 這表明隨著振動頻率增加,水珠在液面上最大停留時間變長是因為振動頻率增加使得液面張力增大所致. 對肥皂水表面張力系數隨振動頻率變化的實驗數據進行二次方擬合得到如下關系方程
α=152.95+0.036f2
(2)

圖4 肥皂水表面張力系數隨振動頻率的變化曲線
4 結論
肥皂水在振動條件下,具有超疏水特性. 當肥皂水濃度由0.025 mol/L增加到0.25 mol/L時,形成穩定水珠所需的最小振動頻率約在30.7 Hz~31.6 Hz范圍內變化,但未發現明顯的變化規律. 在振動頻率f≤60 Hz時,在肥皂水表面穩定水珠最大停留時間很短,且隨著振動頻率的增大沒有明顯變化;但當振動頻率由60 Hz增加至85 Hz時,在肥皂水表面穩定水珠最大停留時間由5 s激增至84 s.
參 考 文 獻
1 Zhang M,Feng S,Wang L,et al.Lotus effect in wetting and self cleaning.Biotribology,2016(5):31~43
2 范細秋,趙曉棟,張鴻海. 具有“荷葉效應”的硅基仿生表面的制備及微摩擦性能. 納米技術與精密工程,2010,8(4):300~306
3 Couder Y,Fort E,Gautier C-H,et al.From bouncing to floating:noncoalescence of drops on a fluid bath.Physical Review Letters,2005,94(17):0031~9007
4 Gilet T,Bush J W M.The fluid trampoline:droplets bouncing on a soap film.Journal of Fluid Mechanics,2009,625:167~203
5 周惟公,等.大學物理實驗(第二版). 北京:高等教育出版社,2014

