一元函數積分計算錯誤類型與錯因分析研究
王瑞聲
(寧德職業技術學院,福建 福安 355000)
對于高等數學而言,我們已然知曉,無論是一元函數還是多元函數.對其積分的正確求解已經成為了解決各種難題的前提,正因為如此,使得微積分成為了數學的一門重要的分支課程與理論基礎.對于積分而言,我們可以簡單地將其理解為是一種分析連續過程累積的方法,連續累積則映射出微積分的真實靈魂,不過在實際的解題過程中,人們也常常忽略其本質,繼而出現了不同種類的計算偏差.
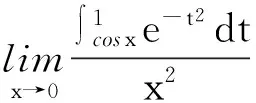
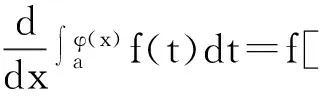
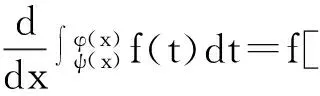
但求解過程中,由于不細心,就會得到一些錯誤的答案.
基于此現象,我們不難知道.對于數學計算來說,它始終貫穿于高等數學的始終,培養大學生準確而迅速的積分計算能力是高等數學教學的一項重要任務.然而在高等數學教學中也存在的不同種類的問題,也就是學生在計算時常常出現這樣或那樣的錯誤,繼而影響解題的正確率[2].學生在學習的過程中,計算方法、解題技巧、基本理論等等的掌握程度,都是解題正確與否的因素.因此有必要對高校大學生在學習微積分時所容易出現的錯誤進行透析,研究其錯誤的原因,提出相關的對策,這樣一來,才能為我們今后的學習或教學保駕護航.
1 一元函數積分計算出錯的類型分析
在高等數學領域中,由于其解題過程的復雜性,錯誤率相對較高,這些錯誤類型也不止局限在解一元函數積分上,在其他學習領域上也同樣存在,下面我們將來分析在解題中容易出現的錯誤類型.
1.1 知識性錯誤
在學習過程中,有時會因為概念不清,出現知識性錯誤.
如f(x) 在[a,b]上有界,在[a,b]中任意插入若干個分點
a=x0 把區間[a,b]分成n個小區間 [x0,x1],[x1,x2],…,[xn-1,xn], 各個小區間的長度依次為 Δx1=x1-x0,Δx2=x2-x1,…,Δxn=xn-1-xn, 在每個小區間[xi-1,xi]上任取一點ξi(xi-1ξixi),作函數值f(ξi)與小區間長度Δxi的乘積f(ξi)Δxi(i=1,2,…,n)并作出和ξi)Δxi,記λ=max{Δx1,Δx2,…,Δxn},如果不論對[a,b]怎樣分法,也不論在小區間[xi-1,xi]上點ξi怎樣取法,只要當λ→0時,和S總趨于確定的極限I,這時我們稱這個極限I為函數f(x)在區間[a,b]上的定積分f(x)dx,即 ξi)Δxi,如果我們不去研究或理解此定義,那么在解題中一定會出現錯誤[3]. 知識性錯誤主要是因為對于某知識點的認識或理解不夠而產生的,而對于數學思維的短板與方法技巧的使用不當,也是產生計算錯誤的一大誘因.或者在解題中思路不對或思維堵塞也會產生計算錯誤. 一般地,對于積分 如果思路堵塞,構建中間因子出錯,那么得到的結果也會不一樣,從而計算錯誤. 除了思維錯誤之外,還有一種在求解過程中導致錯誤的誘因,它就是邏輯性錯誤.所謂的邏輯性錯誤,其實質就是在計算過程中違反正常邏輯從而導致的錯誤[4]. 如果不加以思考,容易得到這樣的錯誤答案.即 根據上述例子,在求解定積分時,如果出現開平方運算時,一般情況下都是根據積分的上下限求解出根式中的函數結果.如果出現邏輯錯誤,就容易忽略被積函數在被積區間中出現正負值的情況,從而導致計算錯誤. 除了心態問題導致的錯誤率之外,不良的學習習慣也是導致計算錯誤率上升的因素.比如在講解積分求解時,在課堂上走神,在注意解題實踐上只在意基本的理論知識.沒有過多的練習,動手與動腦都達不到標準,自己會的題型也不愿意動手,繼而出現眼高手低的尷尬場面.在學習上也不主動,不懂的也不會自動去求問他人,最終導致會做的題做錯,不會做的題無法入手. 只要熟悉相關定義,便可得到解值: 畢竟在求解過程中,無論是什么樣的題型,其變化規律都是根據基本概念向外發散的,其解題的出發點也是建立在基本概念與相關定理上.而高等數學常被運用于科學計算與計算機領域,它需要較高的計算能力.簡言之,著重理解基本概念,是預防或糾正計算錯誤的一大利器,這一點需要我們高度重視. 對于高等數學而言,它不僅有很強的邏輯性,還有一定的復雜性.這也是人們對其青睞與害怕的根源.不過無論多么復雜的知識點,只要有著良好的學習習慣,依次漸進,許多問題都會迎刃而解.不過由于不少學生在平時的學習中,或多或少有著一些不好的習慣,因此在平時的學習或者研究過程中,我們應該培養良好的學習習慣,這不僅是在一元函數積分學中有效,對于其他領域或其他學科都是有效的[5].這需要我們在日常的學習中嚴格要求自己,滲透正確的學習方法,在解題時才能提高正確率. 由此可見,在高等數學中,導致計算的錯誤類型多種多樣,不只是知識性錯誤、數學思維錯誤、心態問題這幾種,還有心理因素、知識點掌握不全面等方面的原因.針對于不同的原因,我們應該采取不同的手段,具體情況具體分析.總的來說,在學習高等數學時,我們需要全面掌握相關的知識理論、基本性質與定理.在理解基本知識的情況下培養解題思維,加大自身的練習量,建立各種題型的反射弧,在解題時切勿粗心大意. 參考文獻: [1]洪小輝.一元函數積分計算錯誤的主要類型及錯因分析——以本院06級學生為例的個案研究[D].北京:首都師范大學碩士學位論文,2008. [2]張軍學,陳香蓮.一元函數求極限常用方法及錯誤分析[J].西安教育學院學報,2002,(3):16-18. [3]董云.淺談可積分一元函數的不定積分的解法[J].華夏星火,2005,(Z1):67-68. [4]王寧,劉生.淺談高等數學不定積分方法的簡單歸類[J].科技創新導報,2011,(4):150. [5]賀皖松,吳娟.高等數學一元函數不定積分求法研究[J].昭通學院學報,2017,(5):12-15.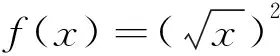
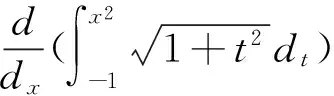
1.2 數學思維錯誤
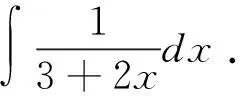
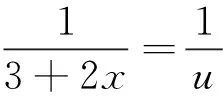
1.3 心態問題
1.4 不良的學習習慣
2 糾正或預防計算錯誤的方法
2.1 加強基礎知識的記憶
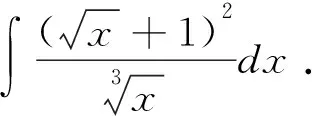
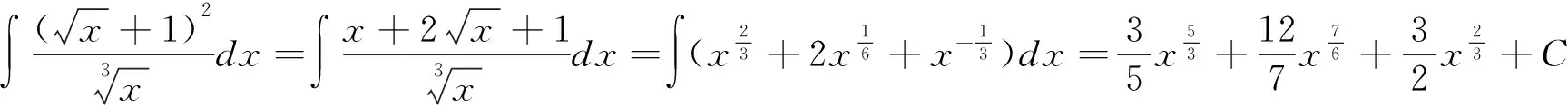
2.2 加強計算訓練
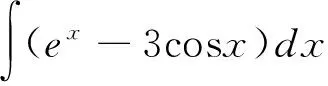
2.3 培養良好的學習習慣
3 小結

