基于極線幾何的統計優化特征匹配算法

2018-05-21 01:24:46趙春暉樊斌田利民胡勁文潘泉

航空學報 2018年5期

趙春暉，樊斌，田利民，胡勁文，潘泉

西北工業大學自動化學院，西安 710072

視覺同時定位與構圖(SLAM)的初始化階段需要利用特征匹配進行三角化得到3D點云[1-2]，特征匹配的準確率和召回率的高低直接影響著3D點云的數量和3D坐標的準確性，進而影響相機位姿的估計精度。

BF(Brute Force)算法[3]通過計算2幅圖像特征點描述子之間的歐式距離，找到最接近的特征點作為候選匹配。但是，由于虛假的檢測，最接近的特征點可能不是真正匹配的特征點。為解決該問題，FLANN(Fast Library for Approximate Nearest Neighbors)算法[4-5]被提出。它利用比率測試來驗證候選匹配特征點對，以剔除虛假匹配。但存在2個主要問題：① 高分辨率圖像的特征點成千上萬，對數千個特征點進行描述是一項艱巨的任務；② 特征點隨機分布的假設并不適用于具有重復結構的圖像，如窗戶、農田等。由于相似的外觀，比率測試拒絕了許多重復結構的特征點。為解決該問題現已提出了一些解決方案，但需要重復結構共面或特征仿射不變等額外的假設和處理步驟[6-8]。RANSAC (RANdom SAmple Consensus)算法[9-11]可以緩解這些問題,但RANSAC本身要求大多數誤匹配應被預先排除,并且當最近距離匹配集合中的誤匹配數量較多時會失效。

羅楠等[12]在研究具有重復結構的圖像匹配方法時，針對基于局部特征的匹配方法容易出現誤匹配以及全局特征點主方向依然通過計算局部特征點相關信息得到等問題，提出了一種基于成對特征點的匹配方法。該方法通過修正特征點的方向信息來提高匹配準確率，啟示了本文特征點主方向的研究。劉威等[13]對ORB(Oriented FAST and Rotated BRIEF)特征采用K近鄰搜索策略來減少誤匹配，利用雙向匹配得到初匹配，對初匹配采用比率法，按照比率升序排列，選擇前若干個匹配對計算RANSAC的模型參數，再計算所有匹配對的誤差和內點數量。該算法利用ORB特征提高計算效率的同時利用最近鄰和次近鄰的比值作為匹配對質量好壞的判斷標準進行篩選，對本文特征點匹配算法的研究提供了很大的參考。Shah等[14-15]選取部分特征點估計基本矩陣，利用對極約束計算每個特征點在目標圖中的極線，利用二維圖像網格化劃分搜索區域以確定候選匹配，最后利用RANSAC去除誤匹配。該算法利用部分特征點計算基本矩陣的思想值得借鑒。

許多特征匹配方法首先使用全局比率測試，然后采用對極約束驗證[16-19]，這樣會先發地拒絕許多重復結構的特征。本文認為，如果在比率測試之前使用對極約束，那么在重復結構上可以保留較多真實的匹配。此外，Sampson距離用于基本矩陣的估計時更為簡單，且對極約束模型的高階項相對一階項較小的時候近似效果會更好[1,20-21]。因此，本文提出了一種基于極線幾何的統計優化特征匹配算法。正確匹配的特征點之間滿足對極約束，它同樣適用于具有重復結構的圖像，而不需要任何假設或復雜的處理。由于基本矩陣的估計需要正確的特征匹配，首先,通過可靠地匹配2幅圖像的特征點子集，利用基于Sampson距離的RANSAC算法來估計2幅圖像之間的基本矩陣；然后，利用對極約束模型優化正確匹配點的大致區域，從而避免由于重復結構增加的誤匹配對，減小特征點搜索區域；最后，利用基于特征點主方向和尺度信息的統計優化算法，得到最終匹配結果。

1 本文所提算法

本文算法首先通過可靠地匹配2幅圖像的尺度不變特征轉換(Scale Invariant Feature Transform,SIFT)特征子集，估計2幅圖像之間的基本矩陣并作為先驗信息。然后對原圖中每一個特征點，利用對極約束優化正確匹配點的大致區域，采用KD(K-Dimension)樹搜索出對應匹配點，并利用雙向匹配反向驗證得到初匹配。對于初匹配，再進一步利用基于特征點尺度和主方向信息的統計優化方法消除誤匹配，得到更精確的匹配結果。算法流程圖如圖1所示。

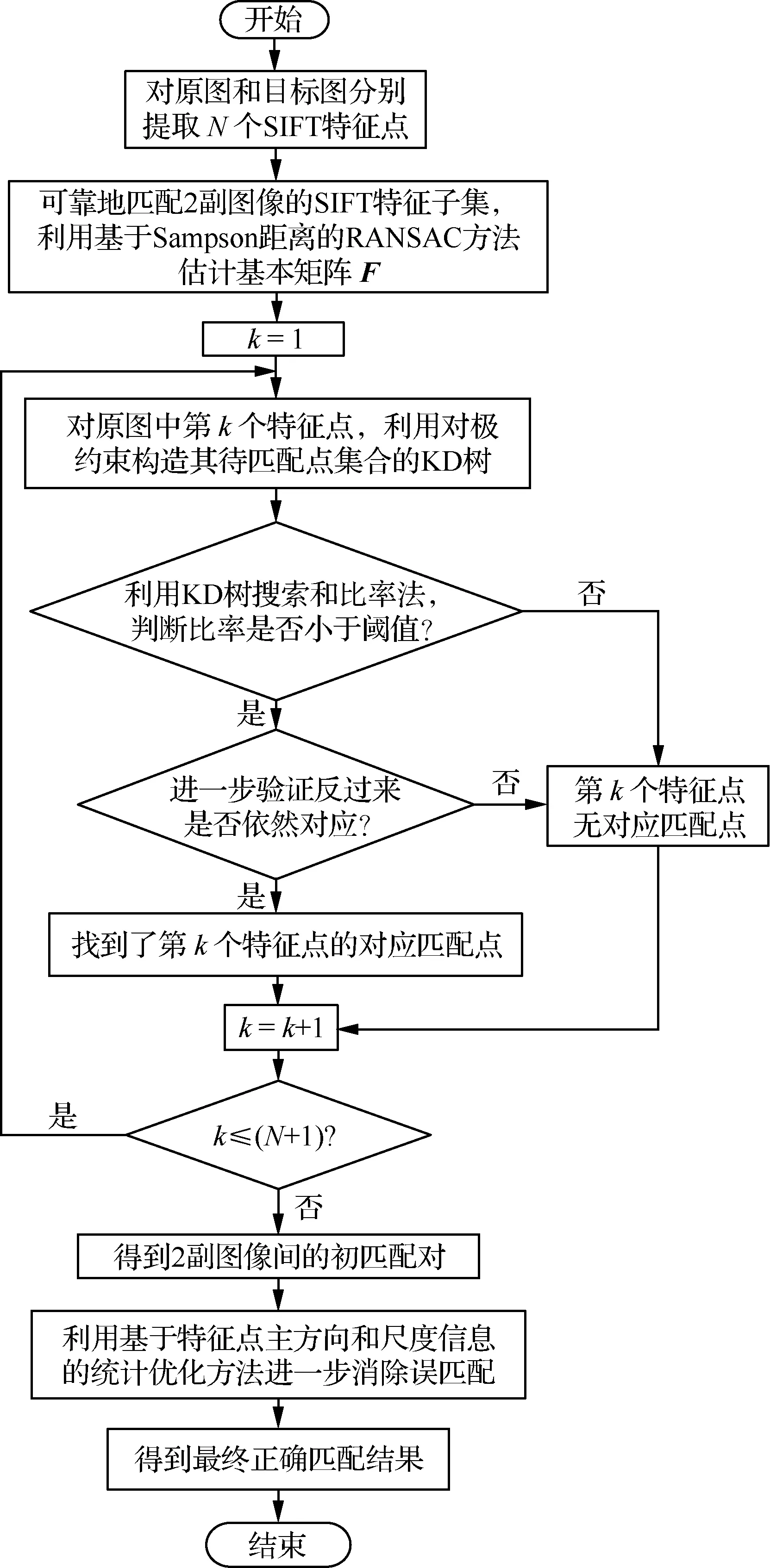
圖1 提出的算法流程圖Fig. 1 Flow chart of proposed algorithm

1.1 算法步驟及原理

步驟1基本矩陣的估計。首先，提取SIFT特征點，利用雙向FLANN匹配方法得到可靠匹配對；然后，利用基于Sampson距離的RANSAC算法估計基本矩陣F。

基于Sampson距離的RANSAC算法為：每次隨機不重復地選擇8組匹配對，利用歸一化8點算法[1]計算基本矩陣F，并分別計算所有的匹配對與對極約束模型之間的Sampson距離，如式(7)所示，若小于閾值，則加入內點集合。經過多次迭代，選擇內點數量最多的集合為最終內點集合，并利用該內點集合結合RANSAC算法估計基本矩陣F。

基本矩陣F是一個3×3的矩陣，有8個自由度，每對匹配點只能得到一個方程，因此計算F至少需要8個匹配對。

構造極線約束的代價函數:

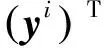
(1)

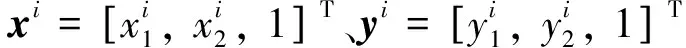
利用泰勒展開式作一階逼近：

(2)

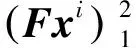
(3)

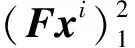
JΔX=-CF(X)

(4)

f(ΔX)=ΔXTΔX-2λ(JΔX+CF(X))

(5)

求解可得

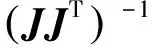
(6)

結合式(3)，可得Sampson距離為

(7)

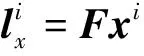
(8)

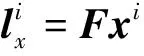
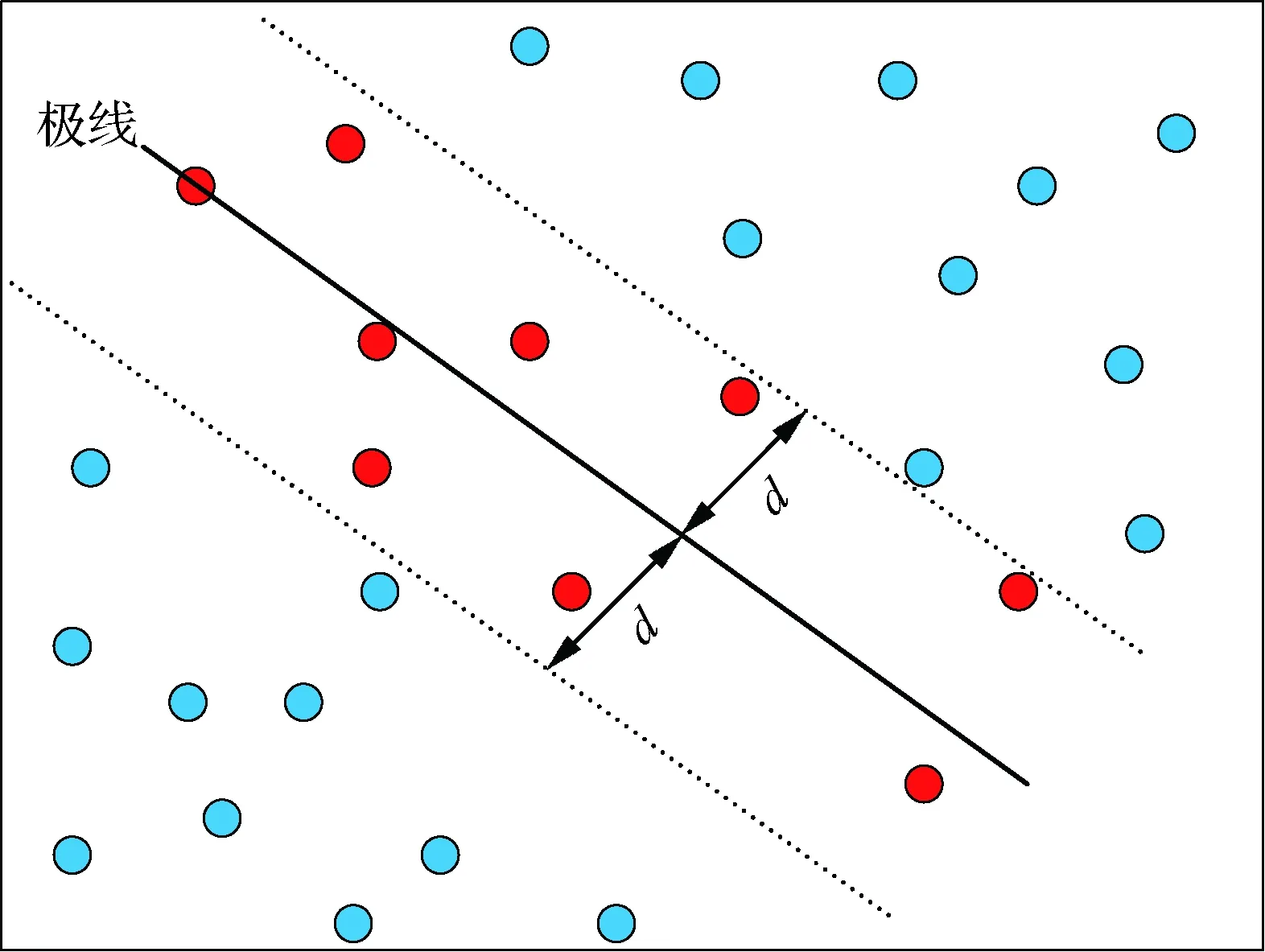
圖2 極線搜索示意圖Fig.2 Schematic diagram of epipolar search

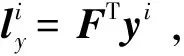
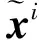
步驟4為了得到更為精確的匹配結果，本文利用基于特征點主方向和尺度信息的統計優化方法進一步消除誤匹配。對于步驟1～步驟3得到的初匹配結果，每次隨機選取一定比例的初匹配結果計算匹配主方向差和尺度比的標準差，若匹配主方向差的標準差大于某閾值，則去除其中的離群值對應的匹配對；若匹配尺度比的標準差大于某閾值，則去除其中的離群值對應的匹配對，不斷迭代，最終得到更加精確的匹配結果。

綜上，本文算法利用對極約束為每個特征點構造了一個較小的待匹配特征點集合，并基于特征點主方向和尺度信息進一步優化匹配結果。而對于原圖某一特征點，傳統特征匹配方法中的待匹配特征點集合是目標圖的所有特征點，此時當在極線外存在與其結構重復的特征點時，傳統方法可能會匹配錯誤。因此本文算法可以減少搜索范圍和重復結構的錯誤拒絕，而且基于特征點主方向和尺度信息可以對初匹配結果進一步優化。

1.2 基于特征點主方向和尺度信息的統計優化

假設提取的某SIFT特征點位置為(x,y)，尺度為σ，如圖3(a)所示，則該特征點所在的尺度圖像為

L(x,y)=G(x,y,σ)*I(x,y)

(9)

式中：*表示卷積；I(x,y)為圖像區域；G(x,y,σ)為高斯核函數，滿足:

(10)

使用有限差分計算以(x,y)為中心、3×1.5σ為半徑的鄰域內每個像素L(x,y)對應梯度的幅值和幅角，即

(11)

利用梯度直方圖統計該鄰域內所有像素的梯度分布特性，其橫軸是梯度幅角(將0°～360°的范圍分為36個柱，每10°一個柱，共36個柱)，縱軸是梯度幅角對應的梯度幅角個數，如圖3(b)所示。最后，通過對直方圖中主峰值和距離它最近的2個柱值進行拋物線插值得到該特征點的主方向θ。

圖4為匹配主方向差的定義示意圖。圖4中：θL為原圖中的特征點fL(實線箭頭)的主方向；σL為原圖對應尺度；θR為目標圖中匹配特征點fR(虛線箭頭)的主方向；σR為目標圖對應尺度。即

θ1=θL

(12)

θ2=(θL+180°)%360°

(13)

定義1匹配主方向差為2個已匹配特征點的主方向之間的夾角α。若目標圖中匹配特征點的主方向位于區域A，則α>0；若目標圖中匹配特征點的主方向位于區域B，則α<0。如圖4所示，即

1) 0°≤θL<180°

(14)

2) 180°≤θL<360°

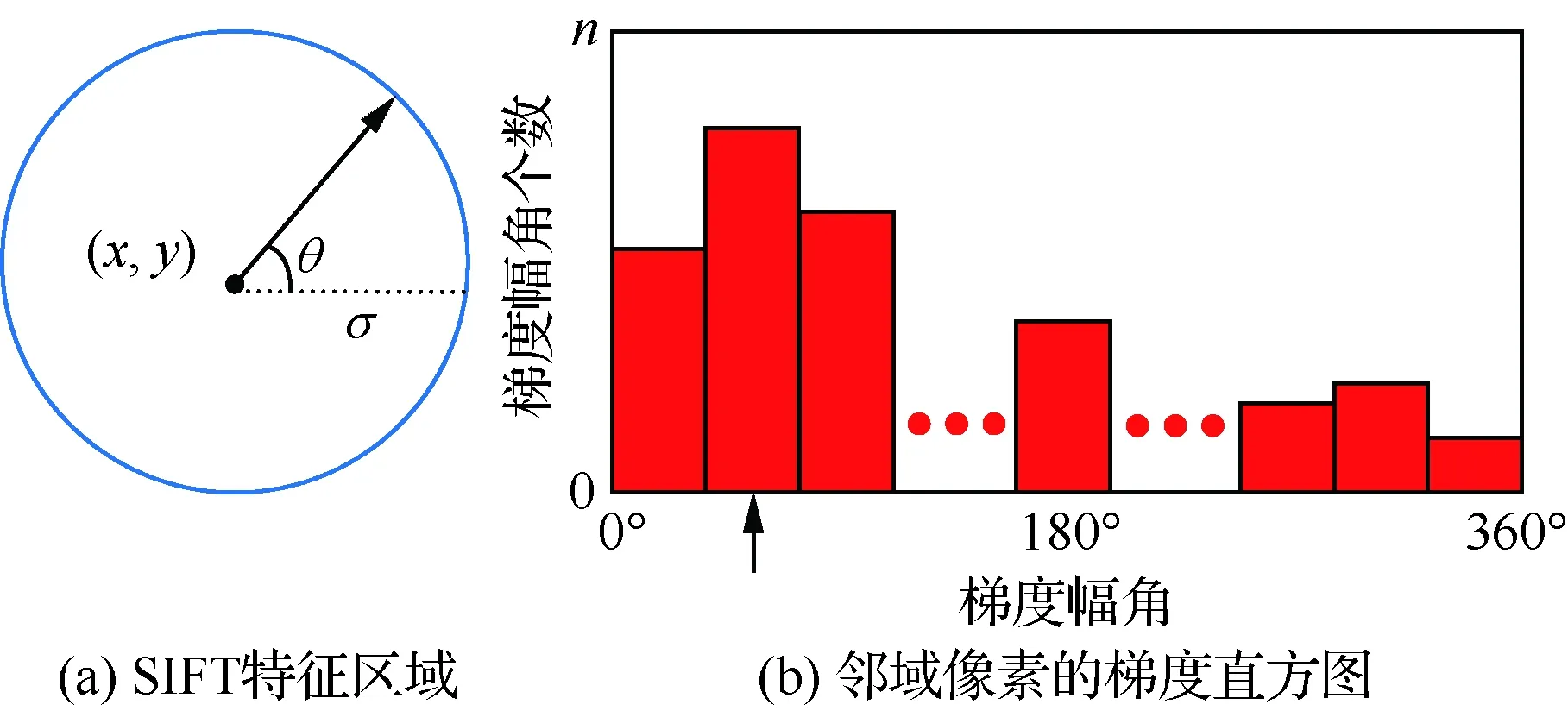
圖3 SIFT主方向的定義示意圖Fig.3 Schematic diagram of definition of SIFT main direction

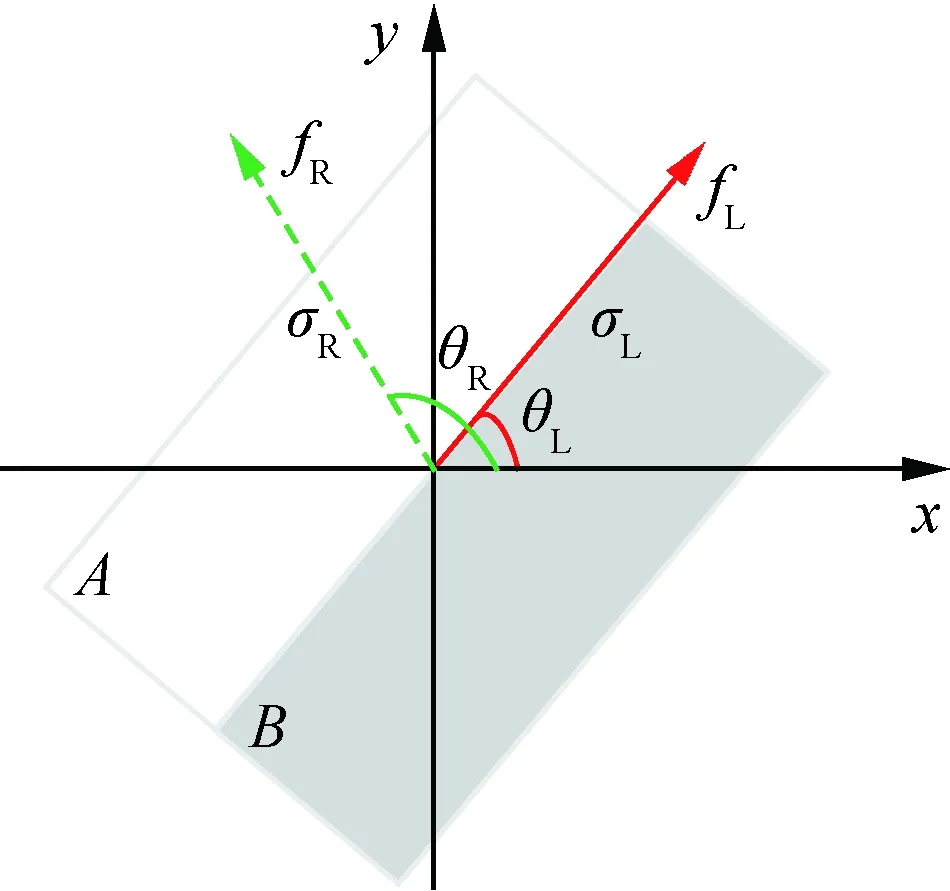
圖4 匹配主方向差的定義示意圖Fig.4 Schematic diagram of definition of main direction difference

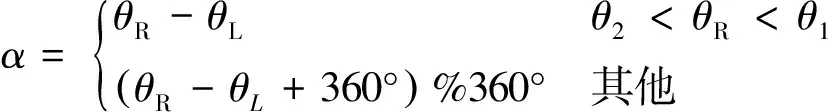
(15)

定義2匹配尺度比為原圖中的特征點的尺度與目標圖中匹配特征點尺度的比值,即

(16)

由定義1可知，匹配主方向差的范圍為-180°～180°。本文采用TUM數據集[22]的freiburg3_long_office_household中的視頻序列圖片，通過大量實驗分析匹配主方向差和尺度比在已匹配特征點對上的分布情況。

分別將目標圖逆時針旋轉90°和縮放0.5倍后與原圖匹配，對匹配點對的尺度比和主方向差進行測試，如圖5所示，其中紅色為無旋轉和縮放變換，藍色為旋轉變換，綠色為縮放變換。

分別將數據集中第0幀與第0,1,…,99幀用BF、FLANN、ROBUST算法進行匹配，統計匹配主方向差和尺度比的標準差的分布，如圖6和圖7所示。

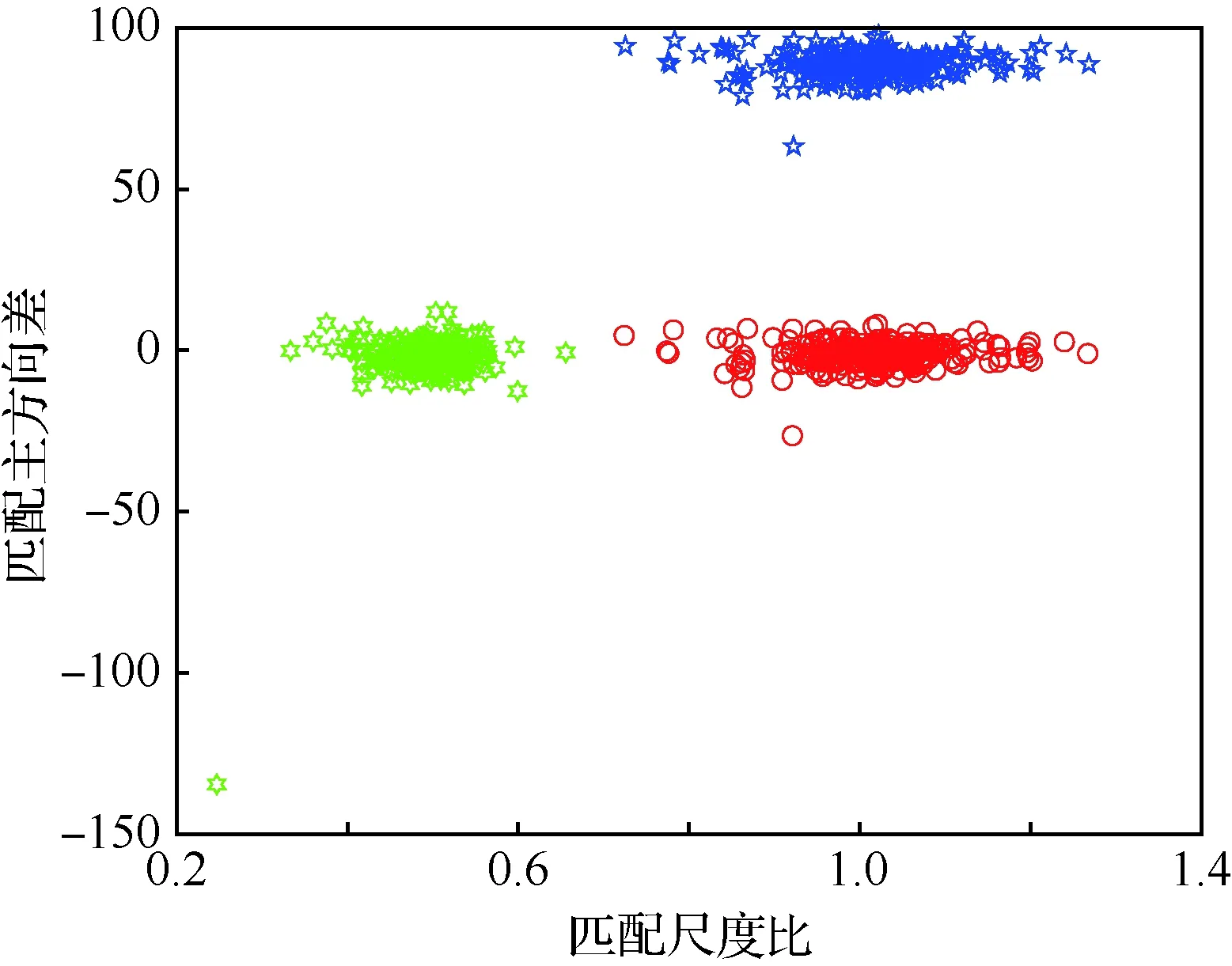
圖5 匹配點對的尺度比和主方向差的分布Fig.5 Distribution of scale ratio and main direction difference of matching features

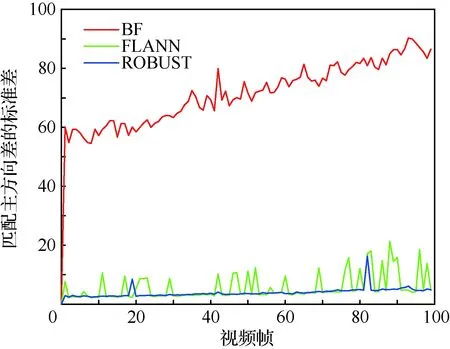
圖6 匹配主方向差的標準差的分布Fig.6 Distribution of standard deviation of main direction difference of matching

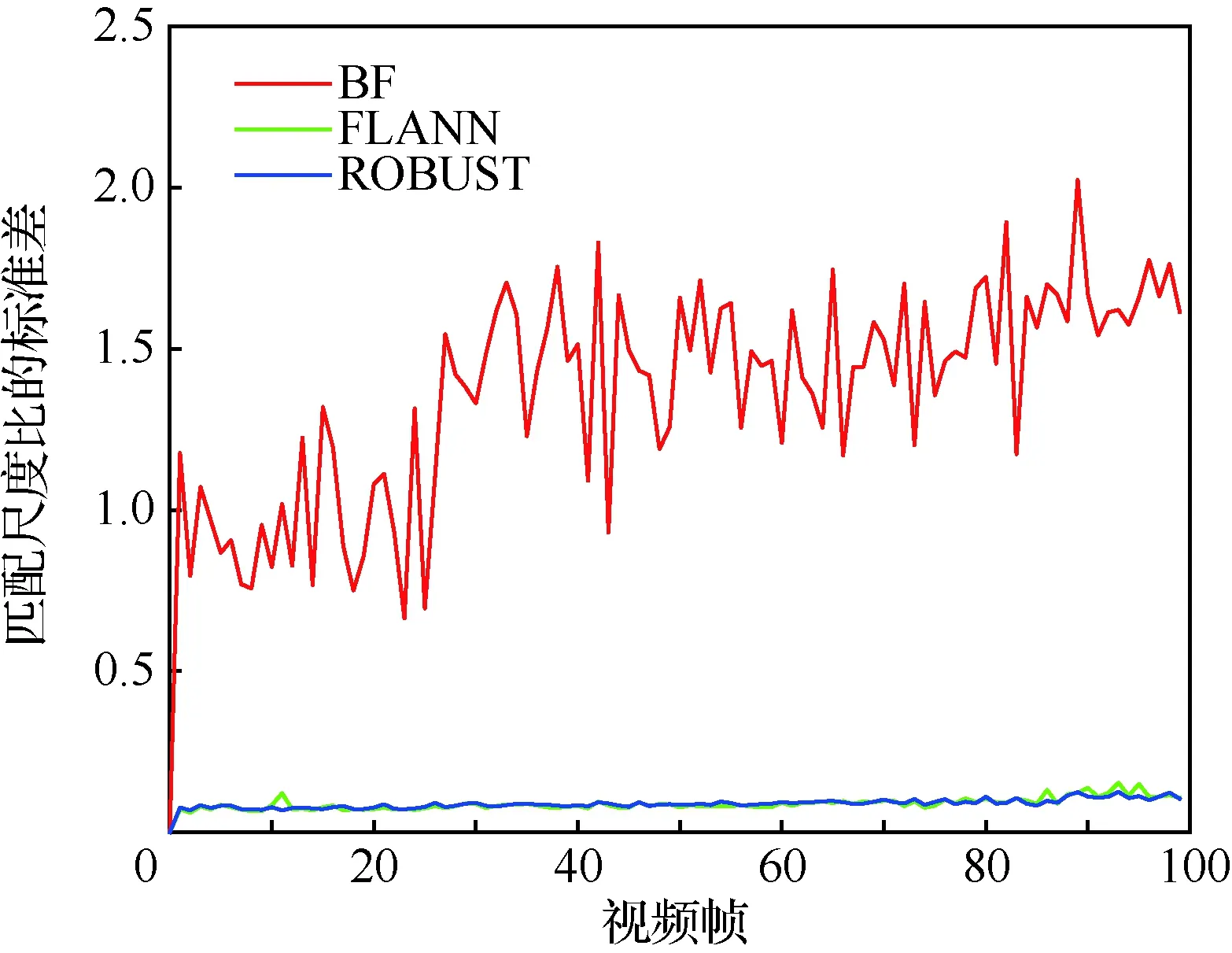
圖7 匹配尺度比的標準差的分布Fig.7 Distribution of standard deviation of scale ratio of matching

由圖5可知，匹配主方向差和尺度比的分布較為集中，但同時也存在少量的孤立點和離群值，這是因為存在誤匹配。

由于BF匹配結果中存在大量誤匹配，即BF匹配主方向差和匹配尺度比中存在大量離群值； FLANN和ROBUST匹配結果中誤匹配較少，其中的離群值相對較少。結合圖6和圖7可知，正確匹配對的匹配主方向差和尺度比的標準差較小，分布較為集中，因此可以利用匹配主方向差和匹配尺度比的標準差判斷初匹配結果是否正確。即，每次從初匹配結果中隨機選取部分匹配結果，計算其匹配主方向差和尺度比的標準差，若匹配主方向差的標準差大于某閾值，可以去除其中的離群值對應的匹配以消除誤匹配；若匹配尺度比的標準差大于某閾值，可以去除其中的離群值對應的匹配以消除誤匹配。

2 實驗和結果

本實驗采用Ubuntu 14.04平臺，基于OpenCV搭建Cmake工程。實驗選取TUM[22]和DTU[23]數據集，如表1所示。實驗閾值設置如表2所示。實驗原圖和目標圖如圖8所示，分別包含模糊、視角變化、光照變化和低紋理等噪聲。

每組實驗的實驗環境分為3部分：原圖像分別與目標圖像(場景1)、目標圖像順時針旋轉90°(場景2)、目標圖像縮放0.5倍(場景3)進行匹配測試，實驗結果如表3所示。

表1 數據集簡介Table 1 Introduction of data sets

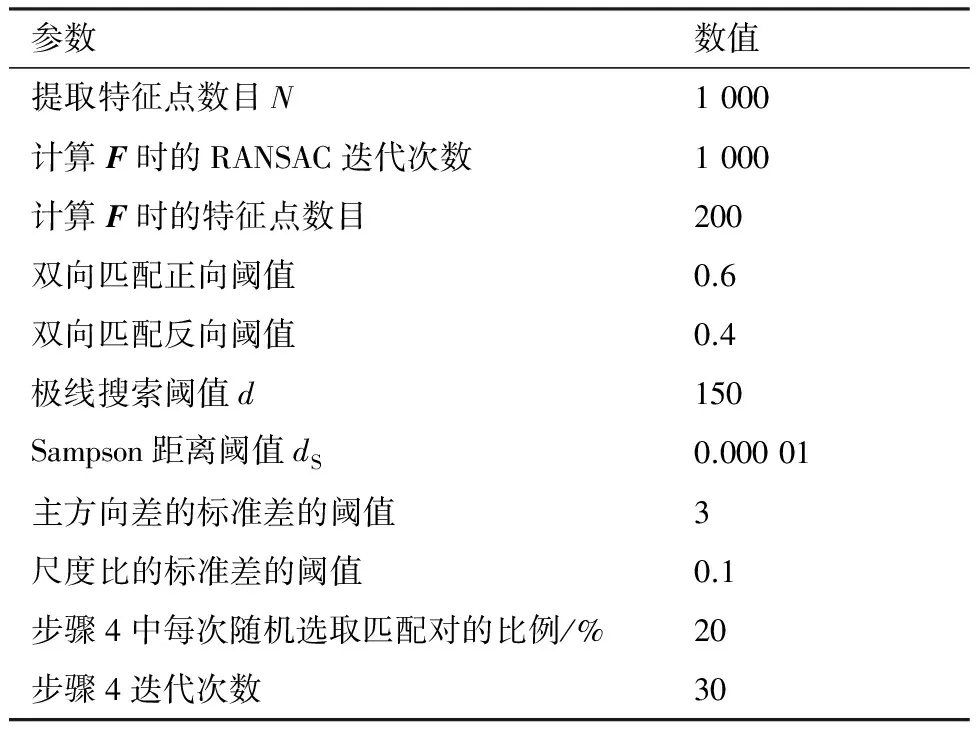
表2 實驗閾值設置Table 2 Experimental threshold setting

圖8 實驗圖像Fig. 8 Images for experiment

結合表3，從圖9可以看出對于重復結構下的匹配，本文算法匹配數量更多。圖10和圖11的匹配結果表明本文方法對圖像的旋轉和縮放變換具有良好的魯棒性。由表3中各種實驗環境下的算法比較可知，本文算法的匹配數量約是FLANN和ROBUST算法的1.2倍，匹配準確率平均提高了1%左右；實驗5的結果也表明對于具有重復結構的圖像間的匹配，本文算法的匹配數量和準確率都有很大的提升。

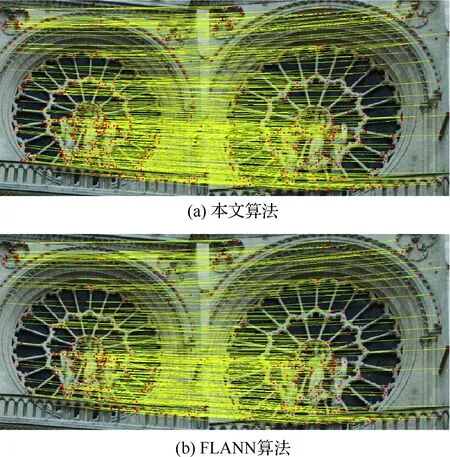
圖9 實驗5重復結構下的匹配結果Fig.9 Experiment 5 matching result in repetitive structure

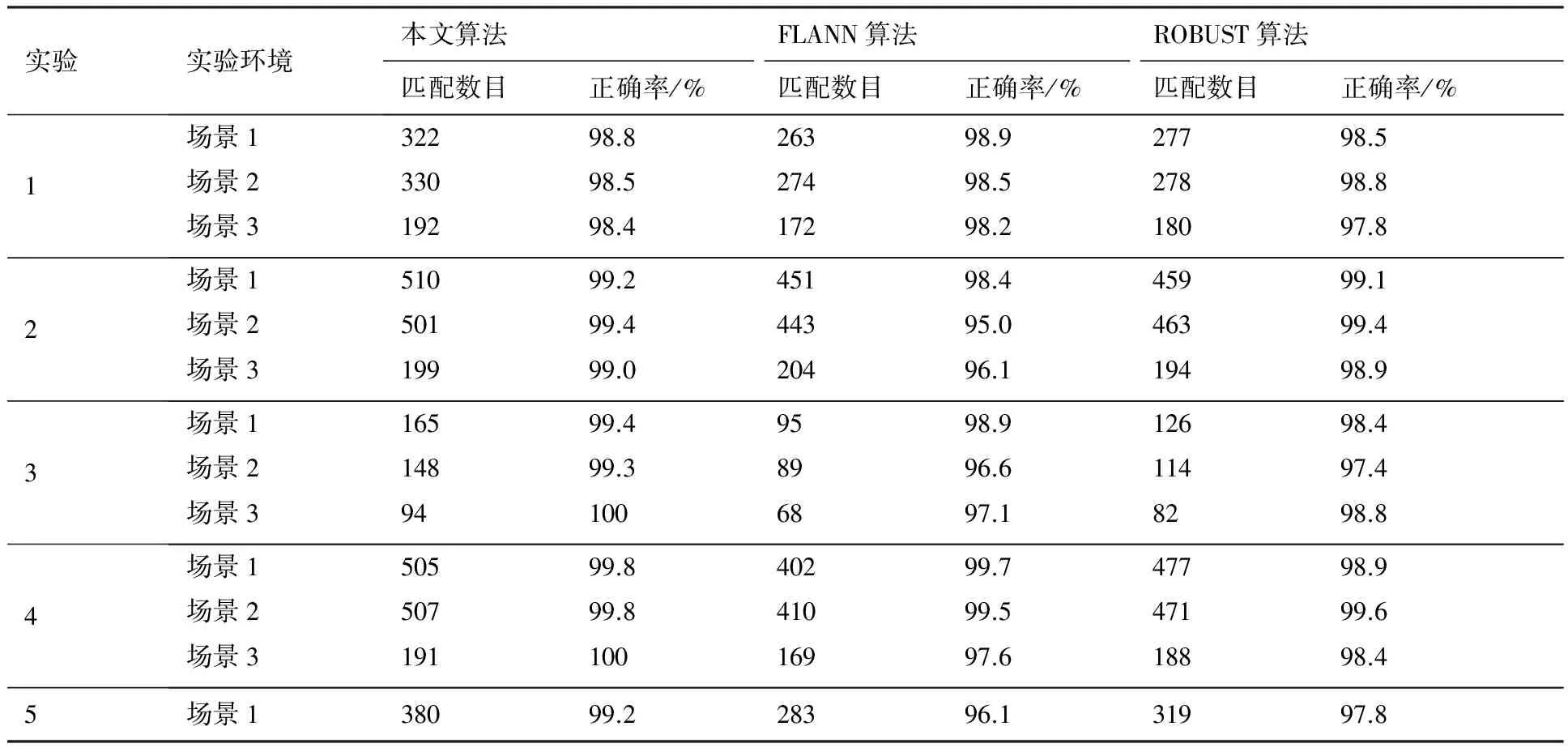
表3 本文算法與FLANN和ROBUST匹配算法的性能比較Table 3 Comparison of performance of proposed algorithm, FLANN and ROBUST matching algorithms

圖10 實驗2匹配結果Fig.10 Mathing results of Experiment 2

圖11 實驗4匹配結果Fig.11 Matching results of Experiment 4

3 結論

1) 本文算法對圖像的旋轉和縮放變換具有良好的魯棒性，匹配數量達到了FLANN和ROBUST算法的1.2倍左右，匹配準確率平均提高了1%左右，并且也能較好地處理具有重復結構的圖像間的匹配。

2) 本文算法的時間復雜度為O(kn2)，計算量相對較大，如何提高本文算法的運行效率和處理嚴重重復結構的能力將是接下來的研究目標。

參考文獻

[1] HARTLEY R, ZISSERMAN A. Multiple view geometry in computer vision[M]. Cambridge: Cambridge University Press, 2003: 191-215.

[2] MUR-ARTAL R, MONTIEL J M M, TARDOS J D. ORB-SLAM: A versatile and accurate monocular SLAM system[J]. IEEE Transactions on Robotics, 2015, 31(5): 1147-1163.

[3] ARYA S, MOUNT D M. Approximate nearest neighbor queries in fixed dimensions[C]∥SODA’93: Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1993: 271-280.

[4] LOWE D G. Distinctive image features from scale-invariant key points[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.

[5] MUJA M, LOWE D G. Fast approximate nearest neighbors with automatic algorithm configuration[J]. International Conference on Computer Vision Theory and Applications (VISAPP), 2009, 2(1): 331-340.

[6] KUSHNIR M, SHIMSHONI I. Epipolar geometry estimation for urban scenes with repetitive structures[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(12): 2381-2395.

[7] ZHANG W, KOSECKA J. Generalized RANSAC framework for relaxed correspondence problems[C]∥Third International Symposium on 3D Data Processing, Visualization, and Transmission. Piscataway, NJ: IEEE Press, 2006: 854-860.

[8] SUR F, NOURY N, BERGER M O. Image point correspondences and repeated patterns[J]. Computer Vision & Pattern Recognition, 2011, 8(2): 216-243.

[9] FISCHLER M A, BOLLES R C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395.

[10] CHIN T J, YU J, SUTER D. Accelerated hypothesis generation for multi-structure data via preference analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(4): 625-638.

[11] 王云麗, 張鑫, 高超, 等. 航拍視頻拼圖中基于特征匹配的全局運動估計方法[J]. 航空學報, 2008, 29(5): 1218-1225.

WANG Y L, ZHANG X, GAO C, et al. The global motion estimation method based on feature matching in video[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1218-1225 (in Chinese).

[12] 羅楠, 孫權森, 陳強, 等. 針對重復模式圖像的成對特征點匹配[J]. 中國圖象圖形學報, 2015, 20(1): 113-124.

LUO N, SUN Q S, CHEN Q, et al. Pair-wise feature points based matching algorithm for repetitive patterns images[J]. Journal of Image and Graphics, 2015, 20(1): 113-124 (in Chinese).

[13] 劉威, 趙文杰, 李德軍, 等. 一種基于ORB檢測的特征點匹配算法[J]. 激光與紅外, 2015, 45(11): 1380-1384.

LIU W, ZHAO W J, LI D J, et al. Feature points matching algorithm based on ORB detection[J]. Laser and Infrared, 2015, 45(11): 1380-1384 (in Chinese).

[14] SHAH R, SRIVASTAVA V, NARAYANAN P J. Geometry-aware feature matching for structure from motion applications[C]∥2015 IEEE Winter Conference on Applications of Computer Vision (WACV). Piscataway, NJ: IEEE Press, 2015: 278-285.

[15] SHAH R, DESHPANDE A, NARAYANAN P J. Multistage SFM: Revisiting incremental structure from motion[C]∥2014 2nd International Conference on 3D Vision (3DV). Piscataway, NJ: IEEE Press, 2014: 417-424.

[16] ZHANG Z, DERICHE R, FAUGERAS O, et al. A robust technique for matching two uncalibrated images through the recovery of the unknown epipolar geometry[J]. Artificial Intelligence, 1995, 78(1-2): 87-119.

[17] 陳潔, 高志強, 密保秀, 等. 引入極線約束的SURF特征匹配算法[J]. 中國圖象圖形學報, 2016, 21(8): 1048-1056.

CHEN J, GAO Z Q, MI B X, et al. SURF feature matching based on epipolar constraint[J]. Journal of Image and Graphics, 2016, 21(8): 1048-1056 (in Chinese).

[18] 李立春, 張小虎, 傅丹, 等. 基于極線局部校正的特征匹配方法[J]. 光學技術, 2008, 34(2): 285-288.

LI L C, ZH X H, FU D, et al. Feature matching algorithm based on rectification of epipolar-line region[J]. Optical Technique, 2008, 34(2): 285-288 (in Chinese).

[19] 張培耘, 華希俊, 夏樂春, 等. 基于 RANSAC 算法的極線約束立體視覺匹配方法研究[J]. 組合機床與自動化加工技術, 2013(11): 20-22.

ZHANG P G, HUA X J, XIA L C, et al. Stereo matching with epipolar line constraints based on RANSAC algorithm[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2013(11): 20-22 (in Chinese).

[20] 單欣, 王耀明, 董建萍. 基于RANSAC算法的基本矩陣估計的匹配方法[J]. 上海電機學院學報, 2006, 9(4): 66-69.

SHAN X, WANG Y M, DONG J P. The matching method based on RANSAC algorithm for estimation of the fundamental matrix[J]. Journal of Shanghai Dianji University, 2006, 9(4): 66-69 (in Chinese).

[21] 田謹思, 蘇劍波. 基于Sampson誤差計算單應的立體匹配[J]. 計算機工程與應用, 2005, 41(3): 7-9.

TIAN J S, SU J P. Stereo matching with epipolar line constraints based on RANSAC algorithm[J]. Computer Engineering and Applications, 2005, 41(3): 7-9 (in Chinese).

[22] STURM J, ENGELHARD N, ENDRES F, et al. A benchmark for the evaluation of RGB-D SLAM systems[C]∥2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Piscataway, NJ: IEEE Press, 2012: 573-580.