混合動力汽車輔助動力單元效率優化控制研究?

羅 勇，劉 莉，譚 偉，葉 明，尹燕麗，劉俊龍

(1.重慶理工大學，汽車零部件先進制造技術教育部重點實驗室，重慶， 400054；2.中國汽車工程研究院股份有限公司，汽車噪聲振動和安全技術國家重點實驗室，重慶 400054；3.重慶交通大學機電與車輛工程學院，重慶 400054； 4.重慶大學，機械傳動國家重點實驗室，重慶 400054)

前言

續駛里程過短導致的“里程焦慮”是制約電動汽車普及的重要因素之一，在電動汽車中加入輔助動力單元(auxiliary power unit，APU)構成增程式電動汽車(extended-range electric vehicle，EREV)是一種可行的解決方案[1-2]。當動力電池SOC下降到一定程度時，APU工作發電，從而提高電動車續駛里程。增程式電動汽車兼備純電動汽車和傳統內燃機汽車的優點，解決了純電動汽車續航里程不足的問題，被公認為傳統汽車向純電動汽車平穩過渡的理想車型，具有廣泛的發展與應用前景[3-4]。

典型的EREV中，APU和驅動電機之間只有電力連接，増程器工作時經歷機械能-電能-機械能之間多次能量轉換，降低了系統效率[5]。本文中提出如圖1所示的EREV結構，APU與驅動電機之間通過離合器L0，L1和齒輪機構連接，可在必要時實現増程器與驅動電機通過機械耦合輸出動力，避免了因多次能量轉換而降低系統效率的問題。該系統還裝備有超大速比變化范圍的回流式無級變速器，可在一定車速范圍內由APU直接驅動車輛，使車輛在電池組故障或斷電時也可行駛到維修點，在緩解里程焦慮的同時大大提高了驅動系統的可靠性。

圖1 增程式電動汽車結構示意圖

在圖1所示的系統中，APU可工作在固定工作點或功率跟隨模式，對APU的控制決定著系統的燃油消耗水平。傳統的APU控制策略只關注在使發動機工作在其高效率區域[6]，實際上，APU效率不但與發動機效率有關，還受發電機效率的影響。發電機效率隨其工況不同而在70%到超過95%之間變化[7]，對APU效率的影響不可忽視。為實現APU效率最佳的控制目標，必須考慮包括發動機和發電機在內的綜合效率。

在分析APU中發動機和發電機效率耦合關系的基礎上，提出發動機與發電機聯合高效工作的APU控制策略。設計優化算法，對不同發電功率需求下發動機與發電機聯合高效工作的目標轉速和轉矩進行計算。建立仿真模型，對發動機與發電機聯合高效工作的策略與傳統控制策略進行仿真對比分析，并進行固定發電功率需求下的臺架試驗驗證。

1 APU發動機與發電機效率耦合分析

要實現任意發電功率需求下APU中發動機與發電機聯合工作效率最優的控制，首先需要分析發動機與發電機效率之間的耦合關系，找出影響二者效率的共同因素作為優化和控制參數。

1.1 發動機效率特性

發動機工作過程復雜，其效率特性難以理論建模，研究顯示發動機效率是其輸出轉速和轉矩的函數[8]。通過試驗測試出不同轉速和轉矩下發動機燃油消耗量be，進而計算出不同轉速和轉矩下發動機效率。根據發動機燃油消耗試驗數據得到發動機效率數值模型，如圖2所示，可表示為

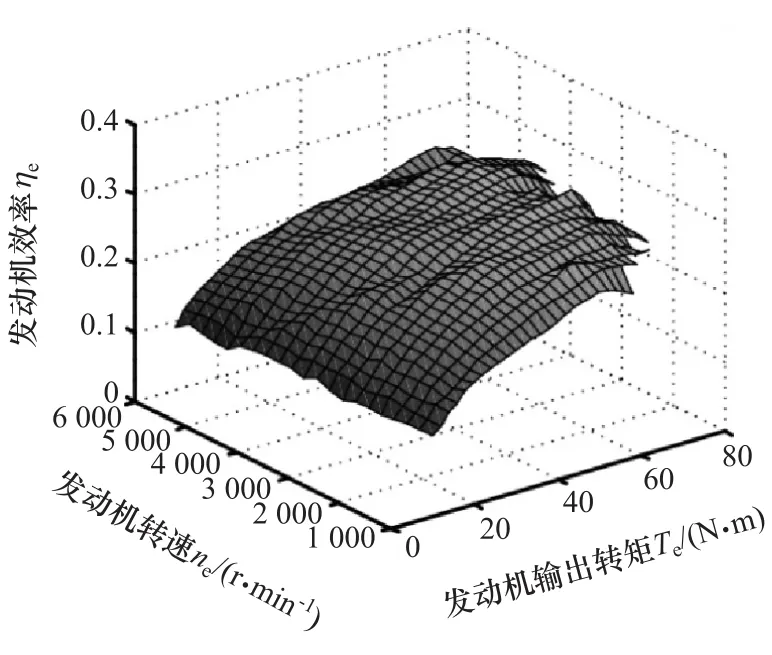
圖2 發動機效率特性

1.2 發電機效率特性

研究顯示，發電機效率是其輸入轉矩和轉速的函數[9]，可表示為ηgc＝f(ngc，Tgc)，通過試驗建立發電機效率數值模型，見圖3。發動機與發電機同軸連接有ngc＝ne，Tgc＝Te，發電機效率可表示為

1.3 APU中發動機與發電機效率耦合關系分析

為實現APU中發動機與發電機聯合工作效率最優控制，須對兩者效率耦合關系進行分析，確定系統狀態參數和影響系統效率的耦合參數，并對效率優化問題進行定義。

APU能量流動與轉化關系如圖4所示，其中Qf為汽油消耗率，Pin為輸入發動機燃油所包含的功率，Pe為發動機輸出功率，Pi為APU輸出的電功率。APU效率最優控制的目標是使汽油消耗率Qf最小，因1W＝1J/s，汽油質量熱值常數R＝46000J/g，故Qf可表示為

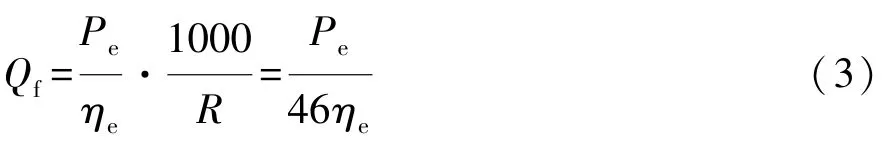
當需求發電功率為Pi，發電機效率為ηgc時，有

將式(4)代入式(3)可得

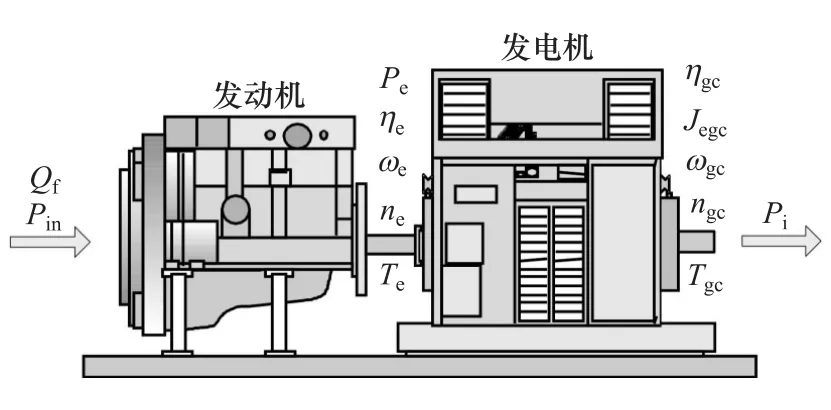
圖4 APU能量流動與轉化關系

設 APU 效率ηsys＝ηeηgc，根據式(5)，要使Qf最小，則要使ηsys最大。ηsys由ηe和ηgc共同決定，傳統策略以發動機效率ηe最大為目標，并不能保證燃油消耗率Qf最小。要實現燃油消耗率最佳的控制，需要以燃油消耗率Qf最小或者系統效率最大為目標對APU控制參數進行優化。

2 APU最佳效率控制優化算法

2.1 優化問題定義

將ηe＝fe(ne，Te)與ηgc＝fgc(ne，Te)代入式(5)可得

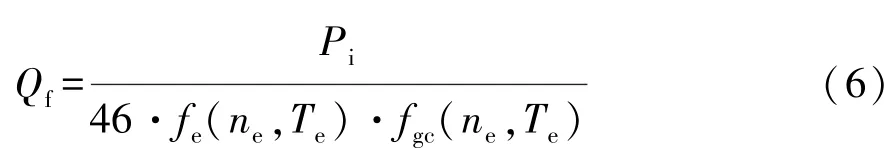
式(6)中需求發電功率Pi由控制器根據車輛狀況由不同控制策略決定，可作為APU系統的狀態參數。ne和Te共同影響著發動機和電機效率，可通過對發動機和發電機的控制實現，看做系統控制參數。APU系統燃油消耗率Qf最小的優化控制問題可描述為：在給定的需求發電功率Pi下，尋找一組最佳的ne和Te目標值，使APU燃油消耗率Qf最小或系統效率ηsys最大。

目標函數：maxηsys

約束條件：

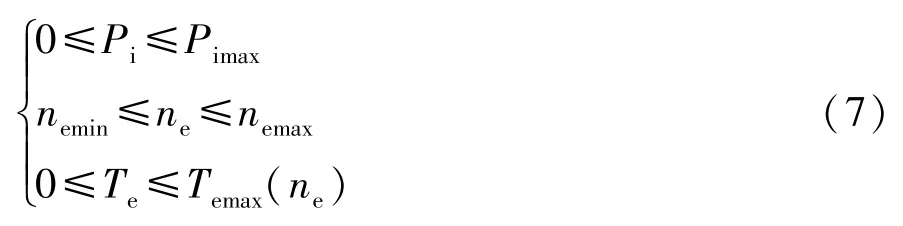
式中：Pimax為最大需求發電功率；nemin，nemax分別為發動機最低轉速和最高轉速；Temax(ne)為轉速ne時發動機最大輸出轉矩。

2.2 優化問題求解

上述優化問題的求解計算量較大，應選用一種效率較高的算法進行求解。與神經網絡等其它優化算法相比，粒子群優化算法具有計算效率高、收斂快和容易編程等優點。選用粒子群優化算法對上述優化問題進行求解，優化流程如圖5所示。

從圖5看出，優化過程總體思路為：對象車輛發電功率范圍為0～45kW，將其以ΔPi為步長等分；在每一發電功率下，采用粒子群優化算法計算出該發電功率下系統效率最高的轉速和轉矩點作為目標工作點；將所有發電功率下系統效率最高的目標轉速和轉矩點存入數表，供控制模塊使用。

在某一發電功率Pij下，采用粒子群優化算法求取系統效率最高的目標轉速和轉矩點的具體步驟如下：

(1)設置粒子初始位置：根據問題規模選取初始粒子數為 10，表示為xi＝(nei，Tei)，i＝0 ∶1 ∶9；在發動機轉速范圍內隨機產生這10個粒子的轉速1000≤nei≤6000；初始轉矩Tei＝neiPi/9550；

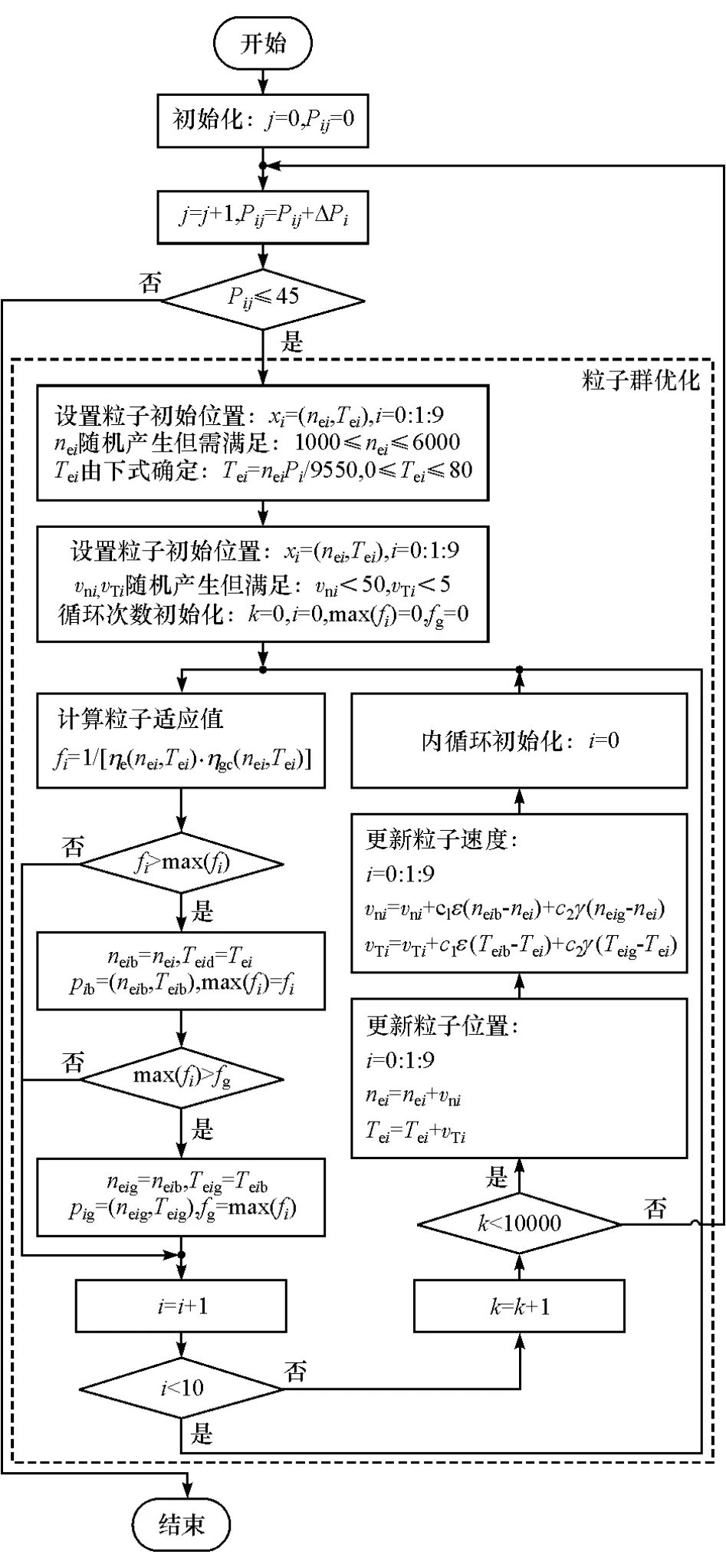
圖5 優化流程圖

(2)設置粒子初始速度：隨機產生所有粒子初始速度vi＝(vni，vTi)，i＝0 ∶1 ∶9，其中vni表示轉速坐標運動速度，vTi表示轉矩坐標運動速度；對優化循環進行初始化k＝0，i＝0，max(fi)＝ 0，fg＝0，其中k為優化循環迭代次數，i為內循環次數，用于處理每一個粒子；max(fi)用于存儲10個粒子各自的歷史最優值，fg用于存儲所有粒子在某發電功率下的歷史最優值；

(3)計算當前粒子適應值，以系統效率作為適應值，計算公式為

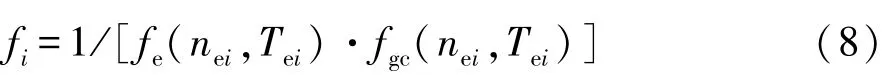
(4)比較當前粒子適應值fi與歷史最優適應值max(fi)，若fi＞max(fi)，則存儲當前位置作為粒子歷史最優位置；

(5)比較粒子歷史最優適應值max(fi)與所有粒子歷史最優值fg，若max(fi)＞fg，則存儲該粒子位置作為所有粒子歷史最優位置；

(6)i＝i+1計算下一個粒子，重復步驟(3)～(5)直到所有粒子計算完畢；

(7)k＝k+1，若k小于設定的優化循環次數則進入下一次循環；

(8) 更新粒子位置nei＝nei+vni，Tei＝Tei+vTi，i＝0 ∶1 ∶9；

(9)更新離子速度：

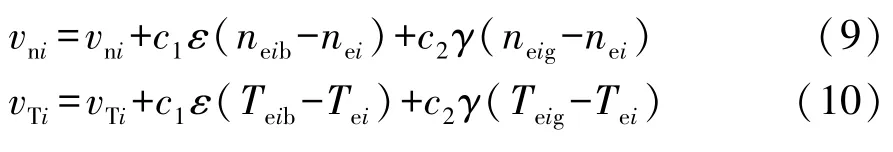
式中c1，c2，ε，γ為常數[10]，更新粒子速度后初始化內循環，進入下一次內循環。

按照上述步驟計算所有發電功率下系統整體效率最佳的目標轉速和轉矩，存入數表。

根據上述算法，采用matlab編寫程序進行優化，圖6為某需求功率下優化過程適應值變化曲線。從圖中可以看出，當循環次數在約600次時算法完成收斂，但為保證算法收斂效果，應適當增加循環次數。不同需求功率下算法收斂的循環次數稍有不同，通過對不同需求功率下適應值變化曲線的分析，當循環次數取1 000時能保證各需求功率下都取得滿意的收斂效果。

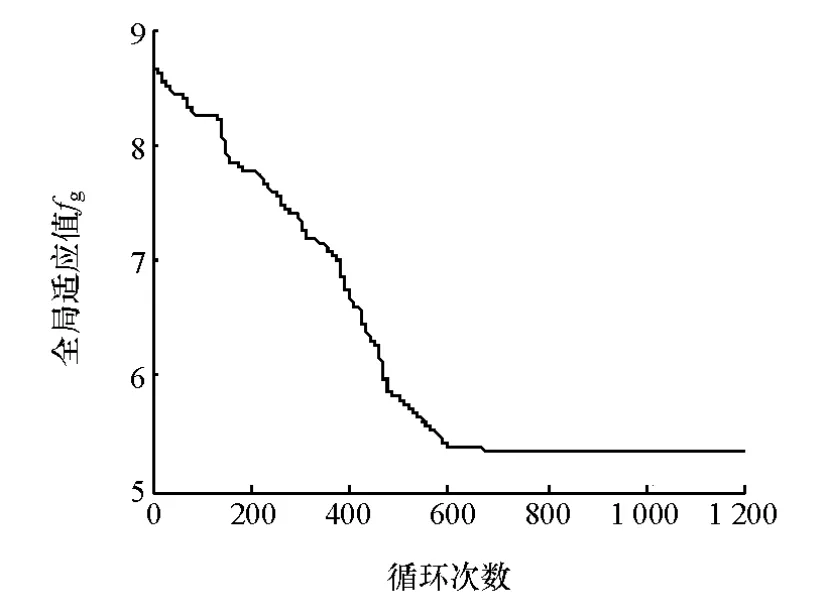
圖6 某需求功率下優化過程適應值變化曲線

2.3 優化結果

取ΔPi＝1進行計算，優化結果如圖7和圖8所示。圖7為優化前后APU目標轉速和轉矩對比圖，根據圖7確定APU目標轉速和轉矩，進而對發動機節氣門開度和發電機變流器實施綜合控制，可實現APU在任意發電功率下均工作在系統效率最高的工作點，達到系統燃油消耗量最小的控制目標。圖7(c)為優化前后系統效率對比，可以看出，在相同電功率需求下，優化后系統整體效率得到提升。

圖7 優化前后APU目標轉速和轉矩

圖8(a)和圖8(b)分別為發動機和發電機的萬有特性圖，圖中曲線a為發動機外特性，b為電機外特性，c為等功率線，d為發動機效率等高線，d1為發電機效率等高線。以功率需求20kW為例，當發動機工作點為圖8(a)中A點時，發動機效率ηeA為該功率下的最高值；由于發動機與發電機同軸連接，發電機工作點的轉速和轉矩與發動機相同，如圖8(b)中 A點，此時發電機效率為ηgcA，系統效率ηsysA＝ηeAηgcA。

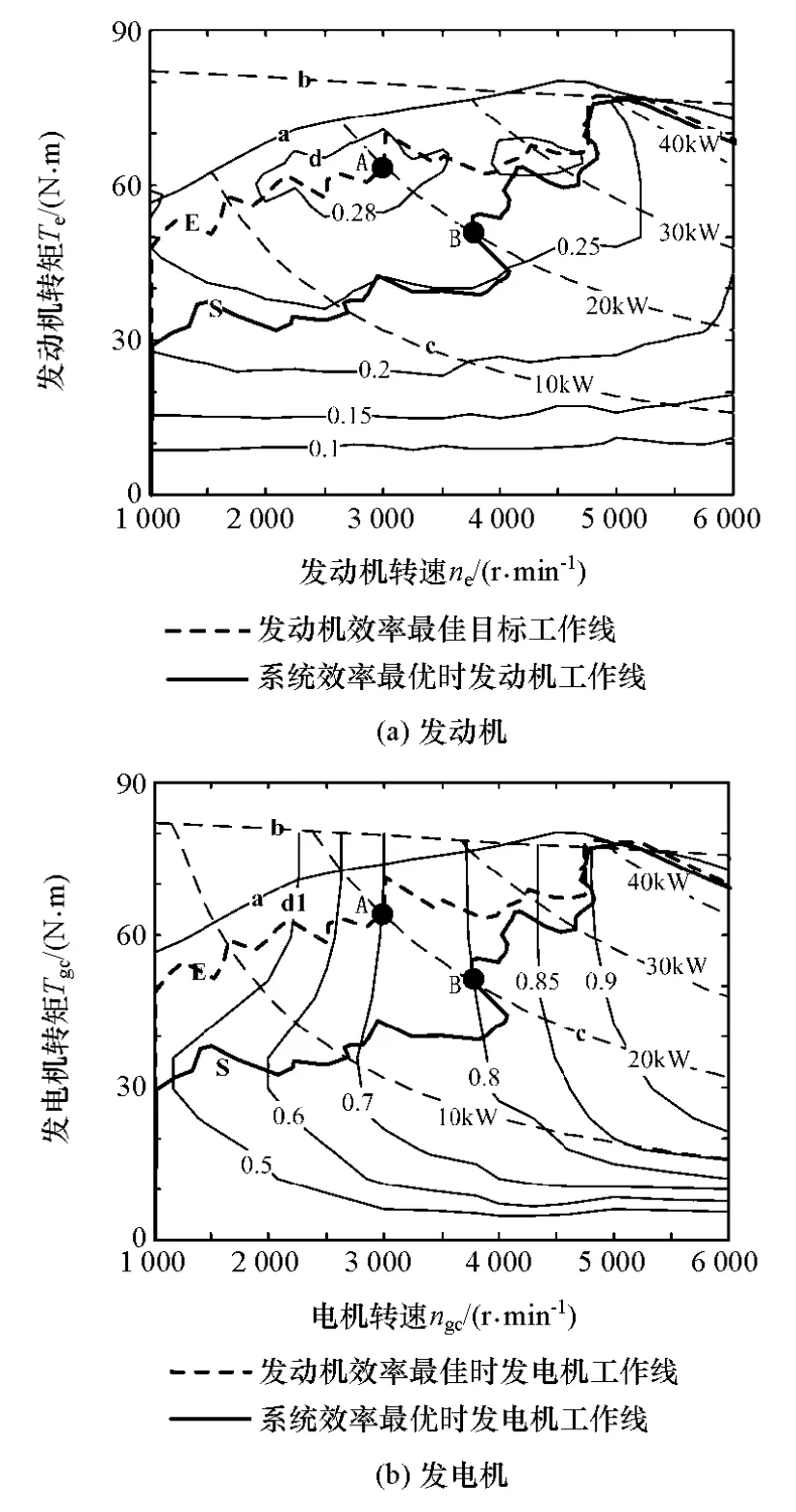
圖8 發動機和發電機萬有特性圖

在20kW等功率線上可能存在這樣的工作點B：雖然工作在點B時發動機效率ηeB小于A點效率ηeA，但工作點B的發電機效率ηgcB大于A點效率ηgcA，且使工作點B的系統效率ηsysB＝ηeBηgcB比 A 點的系統效率ηsysA更大。本文就是要找出各汽車需求功率下這樣的點作為發動機的目標工作點，以真正實現系統燃油消耗量最小的控制目標。

3 系統建模與仿真分析

3.1 控制系統整體結構

要控制APU工作點按照優化的目標工作線運行，須對APU轉速和轉矩實施綜合控制，控制系統結構如圖9所示。整車控制模塊根據當前電池SOC等信息決定APU是否啟動，并決定APU目標發電功率Pi。通常采用的控制策略是APU工作在恒功率發電工況，以利于減小動態工況，提高其經濟性，使APU多工作在穩態工況。APU控制模塊根據輸入的發電功率Pi查優化后的目標轉速表和目標轉矩表，得出APU目標轉速和轉矩；通過控制發動機節氣門開度α實現對轉速的控制，通過控制發電機變流器實現對工作轉矩的控制，通過以上控制使APU工作在優化工作線上。

圖9 控制系統整體結構

3.2 系統建模

APU系統模型如圖10所示，整個系統由發動機、發電機、變流器和動力電池等幾大部分組成。發動機與發電機轉子之間是機械連接，發電機、變流器和動力電池之間是電氣連接。圖中Pe為發動機輸出功率；Jegc為發動機和電機轉動部分轉動慣量；ua，ub，uc為發電機三相定子電壓；ia，ib，ic為發電機三相定子電流；L為發電機定子相電感；R為發電機定子相電阻；Ta1，Ta2，Tb1，Tb2，Tc1，Tc2為變流器 IGBT 功率開關；c為變流器直流側濾波電容；Uc為濾波電容電壓；Ebat為動力電池電壓；rbat為動力電池內阻；ibat為動力電池充電電流。

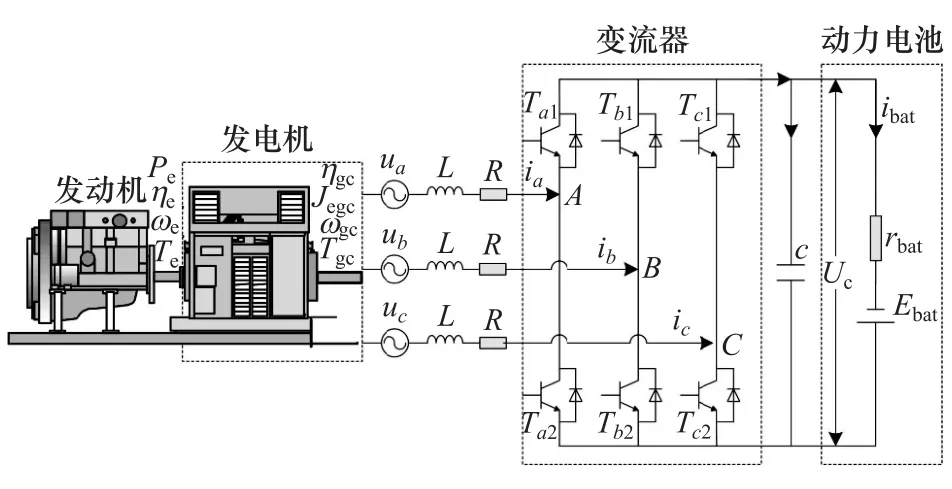
圖10 APU系統模型

采用三相電壓型SVPWM變流器，其6個IGBT功率開關可通過PWM信號控制，實現多種控制目標[11]。IGBT的開關狀態用開關函數表示，開關函數定義如下：

發電機、變流器和動力電池組成的電氣系統采用兩相旋轉坐標系d，q進行描述，從三相靜止坐標系變換到d，q坐標系的變換矩陣為

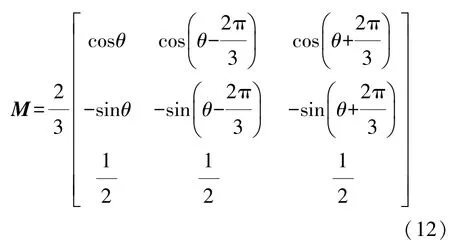
式中：θ為d軸與a軸的夾角，θ＝ωgcpt+θ0；ωgc為發電機機械角速度；p為電機極對數；θ0為t＝0時的夾角。則在d，q坐標系中變流器開關函數為

d，q坐標系下發電機、變流器、動力電池系統電壓方程為

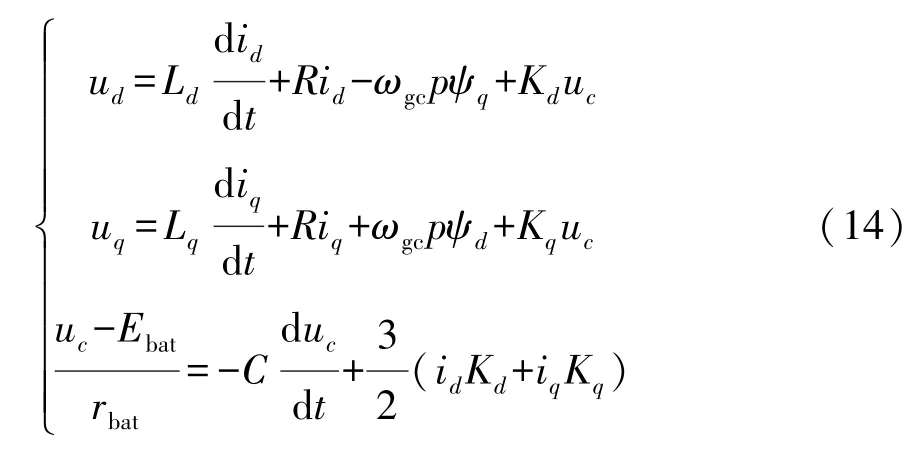
式中：ud，uq為d，q軸電壓；id，iq為d，q軸電流；ψd，ψq為d，q軸磁鏈。d，q軸磁鏈方程為

式中e0為空載反電動勢。發電機電磁轉矩和APU機械方程分別為

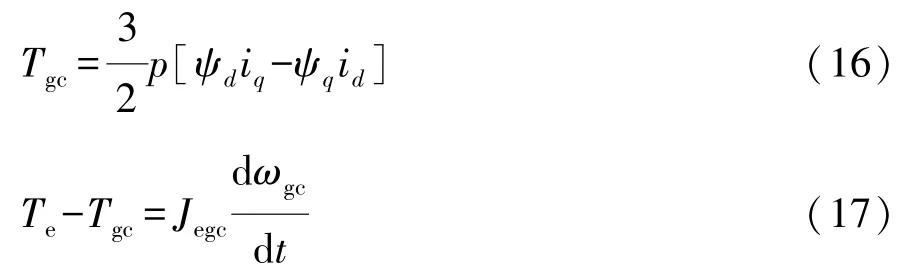
d，q坐標系下電壓電流與固定坐標系下電壓電流的關系為

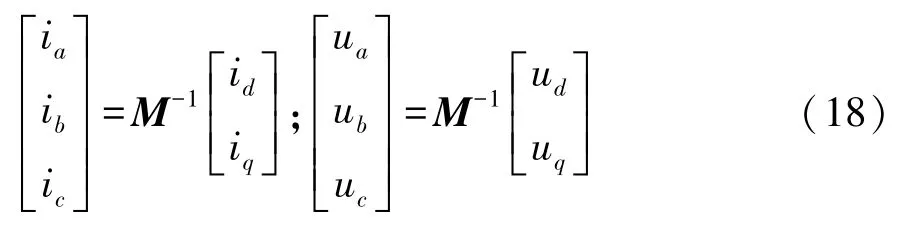
3.3 仿真結果分析

根據理論分析，在matlab/simulink中建立系統仿真和控制模型，對優化前后的APU控制規律進行仿真對比。為驗證優化算法在動態工況下的控制效果，將美國城市循環工況(urban dynamometer drivingschedule，UDDS)下車輛需求功率作為APU發電功率需求輸入系統進行仿真。實際情況下，對APU的功率需求未必按此方法確定，此處由UDDS轉化的功率需求只作為驗證APU控制算法而假定的發電需求曲線。連續2個UDDS工況及其轉化而來的功率需求如圖11所示，仿真結果如圖12和圖13所示。

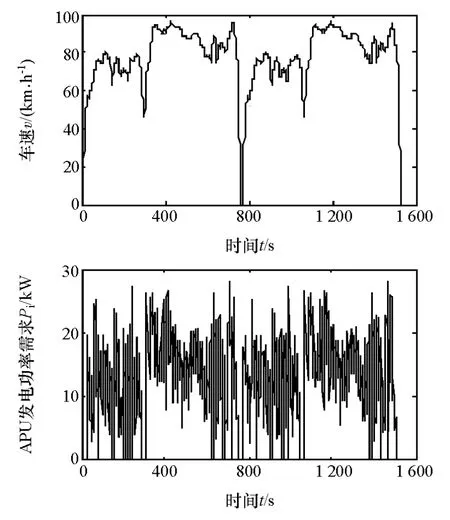
圖11 UDDS工況轉化為模擬發電功率需求

圖12為優化前后發動機和發電機工作點的仿真結果。可以看出，發動機和發電機實際工作點在目標工作線附近波動。圖13為優化前后系統效率的仿真結果。可以看出，與優化前的控制策略相比，當采用優化后的控制策略時發動機效率有所降低，發電機效率有所升高，系統整體效率有所升高，升高幅度在1%～4%左右。

4 試驗研究

為驗證優化控制算法的有效性，在增程式混合動力系統試驗臺上進行試驗研究。試驗臺按照實車配置進行布置，采用電力測功機作為吸能和加載裝置，系統由dspace控制，結構原理如圖14所示，圖15為試驗臺照片。

圖12 發動機和發電機萬有特性及其優化前后工作點

在實車控制中，APU與車輛驅動系統之間只有電氣連接，因而通常使APU工作在發電功率恒定的穩態工況[12]。據此，發電功率分別取為5，10，15，20，25和 30kW，進行穩態工況試驗。 試驗過程為：系統開機并連續運行一段時間進行預熱，使發電機和電池等達到正常工作溫度；控制系統在選定發電功率下連續運行一段時間，記錄系統輸入輸出轉矩、發動機油耗等各種參數；試驗結果分析與對比。

圖16為定發電功率下采用優化控制算法與傳統控制方法時試驗結果對比。圖中發電機效率和發動機效率由實測的轉速和轉矩數據查發動機和發電機效率數值模型得到，由于發動機和發電機效率模型均為試驗獲取的數值模型，故可保證測試數據的可靠性。由圖16可以看出，與傳統發動機效率最高的控制策略相比，采用發動機與發電機聯合高效工作的控制策略后發動機效率有所降低，但發電機效率提高更加明顯，使系統綜合效率在各發電功率下都有不同程度的提高，驗證了優化算法的有效性。

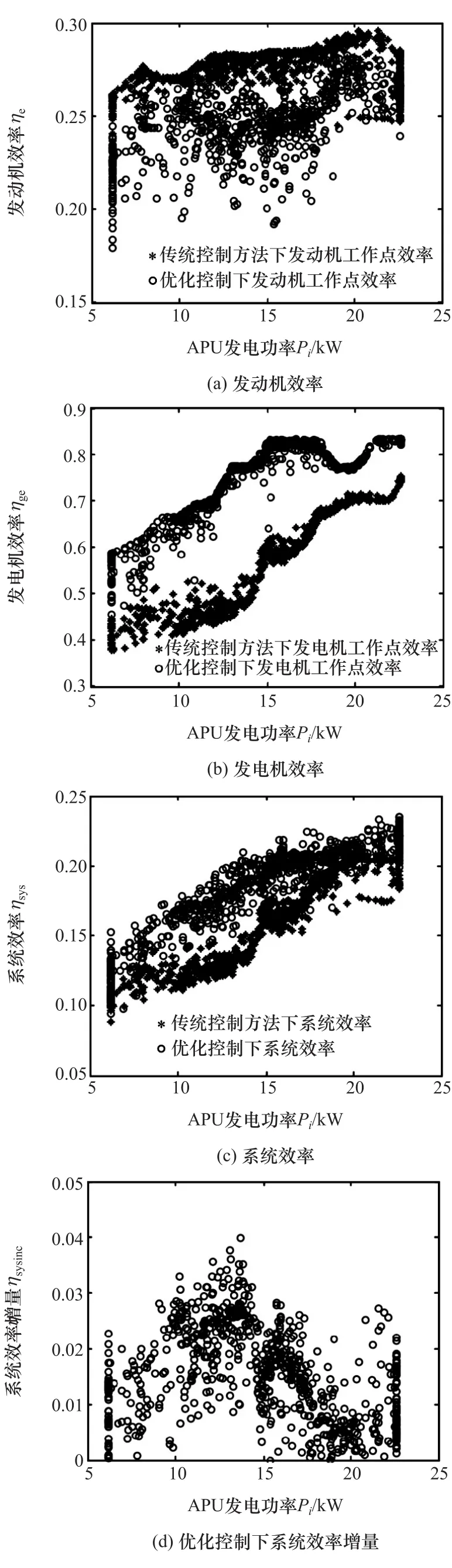
圖13 優化前后系統效率仿真結果

圖14 試驗系統結構原理

圖15 試驗臺

5 結論

(1)針對傳統APU控制只考慮發動機效率的不足，分析了發電機效率對系統燃油消耗量的影響，提出了發動機與發電機聯合高效運行的APU控制思想。

(2)根據優化問題特點，設計基于粒子群算法的優化求解方法，求取不同發電功率下實現發動機與發電機聯合高效工作的APU目標工作轉速和轉矩。

(3)仿真和試驗結果表明，與傳統控制方法相比，優化后發動機效率有所降低，但發電機效率普遍提高，系統整體效率高于優化前。優化后的控制規律在不增加硬件成本的情況下比傳統控制方法可以提高系統效率1%～4%左右。

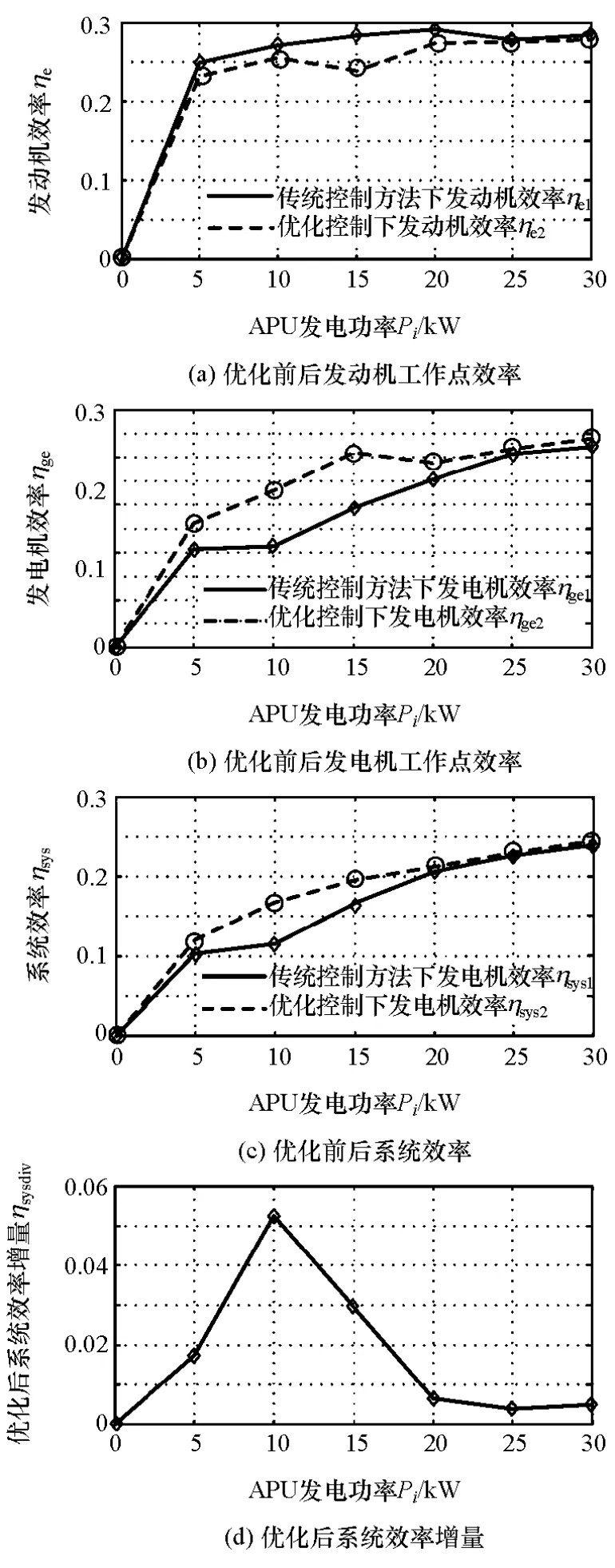
圖16 試驗結果

參考文獻

[1]RHODESK，KOK D，SOHONI P，et al.Estimation of the effects of auxiliary electrical loads on hybrid electric vehicle fuel economy[C].SAE Paper 2017-01-1155.

[2]王斌，徐宏昌，許敏，等.增程型電動汽車的增程器系統控制優化與實驗研究[J].汽車工程，2015，37(4)：402-406.

[3]SHEN Daliang，BENSCH V，MMELLER S.Model predictive energy management for a range extender hybrid vehicle using map information[J].IFAC-PapersOnLine，2016，28(15)：263-270.

[4]LU Liting， MüLLER Steffen.Model predictive speed and headway control with energy optimization for a series hybrid vehicle with range extender[C].4th International Conference on Mechanics and Control Engineering.Lisbon： MATEC Web of Conferences，2015.

[5]謝秀磊.增程式電動車輔助動力單元動態建模及協調控制研究[D].長春：吉林大學，2016.

[6]申永鵬，王耀南，孟步敏，等.增程式電動汽車增程器轉速切換/功率跟隨協調控制[J].中國機械工程，2015，26(12)：1690-1696.

[7]王磊.增程式電動車參數匹配與綜合控制研究[D].重慶：重慶大學，2014.

[8]梁金廣，洪韜汶，宋傳學.混合動力車用汽油機效率模型研究[J].農業機械學報，2012，43(9)：1-10.

[9]CHEN Xueping， ZHANG Hailiang， ZHONG Zaimin， et al.Simulation and user factors analysisof energy consumption of plug-in hybrid electric vehicles[J].Journal of Tongji University，2016，44(11)：1749-1754.

[10]汪定偉，等.智能優化方法[M].北京：高等教育出版社，2007.

[11]丁衛忠.永磁直驅風電變流系統的直接功率控制及通訊功能研究[D].杭州：浙江大學，2015.

[12]MOURA OLIVIRA A，ELVISB，JONY JE，et al.Evaluation of energy recovery potential through regenerative braking for a hybrid electric vehicle in a real urban drive scenario[C].SAE Paper 2016-36-0348.