免疫粒子群優(yōu)化的DV-Hop定位算法

吳珍珍，方旺盛

(江西理工大學(xué) 信息工程學(xué)院，江西 贛州 341000)

0 引言

WSN節(jié)點(diǎn)定位技術(shù)是WSN應(yīng)用于目標(biāo)監(jiān)測、目標(biāo)識別和目標(biāo)跟蹤的支撐技術(shù)，其算法可分為基于非測距(Range- free)的算法和基于測距(Range-based)的算法[1]，其中非測距DV-Hop算法因具有成本低、能耗小、算法實(shí)現(xiàn)簡單等特點(diǎn)而被廣泛應(yīng)用，但該算法也存在定位誤差較大的不足。

為了提高DV-Hop算法的定位精度，國內(nèi)學(xué)者對此引入群體智能算法進(jìn)行優(yōu)化。文獻(xiàn)[2]提出了一種改進(jìn)的粒子群優(yōu)化DV-Hop算法，從慣性權(quán)重的計(jì)算、粒子速度的更新等方面對粒子群算法進(jìn)行改進(jìn)，提高算法的搜索速度，再采用改進(jìn)粒子群算法優(yōu)化節(jié)點(diǎn)的定位結(jié)果，降低了定位誤差。文獻(xiàn)[3]利用免疫系統(tǒng)里的調(diào)節(jié)機(jī)制來提高種群的多樣性，避免了過早陷入局部最優(yōu)解，優(yōu)化的DV-Hop算法提高了定位效果，但該算法未考慮粒子群算法的收斂速度問題。文獻(xiàn)[4]使用遺傳機(jī)制中的前攝估計(jì)縮小粒子搜索范圍，再用改進(jìn)粒子群算法以代替最小二乘法優(yōu)化了DV-Hop算法定位精度。本文根據(jù)免疫粒子群算法的特點(diǎn)，利用該算法來優(yōu)化DV-Hop定位算法求解未知節(jié)點(diǎn)的坐標(biāo)。

1 DV-Hop定位算法

1.1 基本原理

DV-Hop(Distance Vector-Hop)是一種非測距定位算法。該算法依賴于節(jié)點(diǎn)間的互相通信，具體定位算法由3個(gè)階段組成[5]：

第一階段：信標(biāo)節(jié)點(diǎn)通過全網(wǎng)泛洪廣播數(shù)據(jù)包，所有節(jié)點(diǎn)可以記錄下到每個(gè)信標(biāo)節(jié)點(diǎn)的最小跳數(shù)。

第二階段：估算從未知節(jié)點(diǎn)到信標(biāo)節(jié)點(diǎn)的跳距。

第三階段：利用三邊測量法或最小二乘法等計(jì)算未知節(jié)點(diǎn)坐標(biāo)[6]。

1.2 定位誤差的分析

從DV-Hop的工作原理可知，其產(chǎn)生定位誤差的主要原因有跳數(shù)、平均每跳距離、定位的計(jì)算方法等。

(1)跳數(shù)信息不合理

WSN在定位時(shí)通過使用跳數(shù)信息計(jì)算節(jié)點(diǎn)之間的距離，而無線傳感器網(wǎng)絡(luò)中的節(jié)點(diǎn)大都是隨機(jī)分布，未知節(jié)點(diǎn)與錨節(jié)點(diǎn)之間并非都是直線距離，所以節(jié)點(diǎn)之間存在彎曲路徑，將會(huì)導(dǎo)致較大誤差。

(2)平均跳距的估計(jì)值不準(zhǔn)確

在DV-Hop定位算法中，節(jié)點(diǎn)間的距離計(jì)算是采用同一個(gè)平均距離的估計(jì)值乘以對應(yīng)的跳數(shù)來計(jì)算的，存在一定的定位誤差。

(3)定位的計(jì)算方法累計(jì)誤差

計(jì)算未知節(jié)點(diǎn)的坐標(biāo)時(shí)經(jīng)常采用三邊測量和極大似然估計(jì)法。三邊測量方法雖然降低了計(jì)算量，但其受限于第二階段的跳距估計(jì)。而在最大似然估計(jì)法求解過程中需要較多的浮點(diǎn)預(yù)算，計(jì)算開銷帶來的功耗不容忽視。

2 免疫粒子群優(yōu)化的DV-Hop定位算法

鑒于上述誤差分析，針對經(jīng)典DV-Hop定位算法在計(jì)算未知點(diǎn)坐標(biāo)上存在較大誤差，本文提出了一種免疫粒子群優(yōu)化的DV-Hop定位算法。

2.1 粒子群算法進(jìn)化模型

粒子群優(yōu)化(Particle Swarm Optimization,PSO)算法是1995年由Kennedy和Eberhart提出的一種新型的隨機(jī)群體智能的進(jìn)化算法[7]。其原理為：在D維空間里有很多“粒子”，這些“粒子”通過“位置+速度”模型來更新自身的位置與速度，每個(gè)粒子不斷地搜索迭代，向最優(yōu)值位置不斷地靠近[8]。該算法存在以下缺點(diǎn)：(1)容易陷入局部極小值，導(dǎo)致得不到全局最優(yōu)解；(2)沒有充分的優(yōu)選機(jī)制，收斂速度較慢。本文為了提高粒子群算法的全局搜索能力，借鑒免疫算法的思想改進(jìn)PSO算法，當(dāng)PSO算法陷入局部最優(yōu)解時(shí)，通過免疫抗體的選擇、促進(jìn)和抑制機(jī)制產(chǎn)生新的粒子空間，使該算法跳出局部最優(yōu)值，避免“早熟”；另外生成的免疫記憶細(xì)胞可以加快收斂速度，確保快速收斂于全局最優(yōu)解。

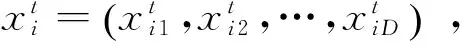
(1)

(2)

式中，c1表示個(gè)體學(xué)習(xí)因子，c2表示全局學(xué)習(xí)因子，而r1和r2為(0,1)上均勻分布的隨機(jī)數(shù)；ω為慣性權(quán)重，表示粒子運(yùn)動(dòng)的趨勢，對全局搜索和局部搜索起到平衡作用[9]。該系數(shù)按照公式(3)進(jìn)行更新。

(3)

2.2 免疫機(jī)制

免疫機(jī)制源于生物免疫系統(tǒng)，其具體思路為將待優(yōu)化適應(yīng)度函數(shù)最優(yōu)解看作入侵生命體的抗原，而免疫系統(tǒng)產(chǎn)生的抗體即為候選解，將個(gè)體最優(yōu)解以免疫記憶形式保存于記憶細(xì)胞，提高收斂速度；根據(jù)免疫調(diào)節(jié)機(jī)制，選擇具有親和度高且濃度低的抗體進(jìn)化，而親和度低濃度高的抗體加以抑制[10]；通過抗原抗體相互促進(jìn)抑制來維持抗體的多樣性，克服了粒子群算法在實(shí)際工程優(yōu)化計(jì)算中的早熟收斂現(xiàn)象，提高了算法的全局搜索效率。

(1)親和度

親和度[11]用來衡量抗原與抗體間的匹配程度，即所求的解與最優(yōu)解的接近程度，記為aff，計(jì)算公式如下：

(4)

其中，f(xi)為xi的適應(yīng)度函數(shù)，η為(0,1)上的常數(shù)。由上式可以看出，當(dāng)f(xi)越小時(shí)，抗體的親和度越大，所求的解與最優(yōu)解就越逼近。

(2)濃度

濃度表示抗體與其相似的粒子在群體中所占的比例，反映種群多樣性的程度。假設(shè)存在i個(gè)抗體x1,x2…,xi，每個(gè)抗體按照親和度從小到大排序并分成m個(gè)等份區(qū)間，其中m=1,2,…，m。計(jì)算每個(gè)區(qū)間的抗體數(shù)，記為sum(m)，得到每個(gè)區(qū)間的濃度為sum(m)/m，將每個(gè)抗體的濃度定義為該抗體所在區(qū)間的濃度，記為D，則有：

(5)

由上式可知，同一個(gè)區(qū)間上的抗體濃度是相同的，這使得抗體濃度越高反而越受到抑制，而抗體濃度越低反而得到進(jìn)化的機(jī)會(huì)。

(3)選擇概率

選擇概率是指抗體在進(jìn)化過程中得到促進(jìn)發(fā)展的概率。假設(shè)基于親和度的選擇概率為Pa，而基于濃度的選擇概率為Pd，計(jì)算公式如下：

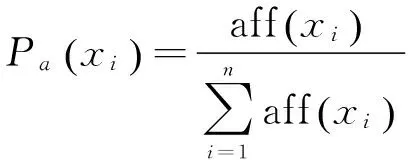
(6)

(7)

則抗體被選中的選擇概率P為：

P(xi)=αPa(xi)+(1-α)Pd(xi)

0<α,Pa,Pd<1

(8)

式中i=1,2,…,n；α為免疫協(xié)調(diào)因子，用來協(xié)調(diào)概率Pd和Pa的權(quán)重。從式(8)可以得知，濃度越高、親和力越低的抗體被選擇的概率越小；而濃度越低、親和力越高的抗體獲得進(jìn)化的概率越大。這樣既提高了抗體的親和度，又保證了粒子的多樣性，從而得到較大的解空間。

(4)適應(yīng)度函數(shù)

適應(yīng)度函數(shù)即目標(biāo)函數(shù)，用來評價(jià)給出的候選解(抗體)的優(yōu)劣。計(jì)算公式如下：

(9)

其中，M(M≥3)為未知節(jié)點(diǎn)接收到的信標(biāo)節(jié)點(diǎn)的個(gè)數(shù)；(x,y)和(xi,yi)分別表示粒子位置和第i個(gè)信標(biāo)節(jié)點(diǎn)的坐標(biāo)；di為未知節(jié)點(diǎn)到信標(biāo)節(jié)點(diǎn)i的歐式距離。適應(yīng)度函數(shù)f(i)的極小值點(diǎn)則為最優(yōu)的定位坐標(biāo)。

3 免疫粒子群優(yōu)化的DV-Hop定位算法步驟

本文算法優(yōu)化的DV-Hop算法步驟如下：

(1)初始化網(wǎng)絡(luò)區(qū)域、節(jié)點(diǎn)總數(shù)、粒子群相關(guān)參數(shù)。

(2)根據(jù)經(jīng)典DV-Hop算法的第一和第二階段獲得每個(gè)信標(biāo)節(jié)點(diǎn)和未知節(jié)點(diǎn)的最小跳數(shù)以及信標(biāo)節(jié)點(diǎn)i的平均跳距，計(jì)算跳段距離。

(3)初始化粒子群。初始化粒子位置X、粒子速度V、歷史局部最優(yōu)位置pbesti=Xi，計(jì)算種群的適應(yīng)度函數(shù)值，取該值的最小值為粒子群的全局最優(yōu)位置gbesti的初始值。

(4)免疫記憶。將粒子按親和度從小到大排序,取親和度較大的粒子存入免疫記憶細(xì)胞中。

(5)利用式(1)、式(2)分別更新粒子的飛行速度和位置，產(chǎn)生n個(gè)新的抗體，然后從免疫記憶細(xì)胞中抽取q個(gè)抗體，組成規(guī)模為n+q的抗體群。

(6)免疫替換，丟棄位置較差的粒子(抗體)。利用式(4)～(8)計(jì)算抗體的選擇概率，依據(jù)選擇概率從n+q個(gè)抗體中選擇出n個(gè)抗體，則選擇概率大的抗體將被選中，組成新的抗體群，從而實(shí)現(xiàn)抗體的多樣性，避免出現(xiàn)“早熟”。

(7)根據(jù)式(9)計(jì)算抗體的適應(yīng)度大小，比較所有粒子當(dāng)前的適應(yīng)度值F(Xi)和局部最優(yōu)位置適應(yīng)度值F(pbesti)，若F(pbesti)>F(Xi)，則更新pbest值;再用更新后局部最優(yōu)適應(yīng)函數(shù)值F(pbesti)與全局最優(yōu)位置的適應(yīng)函數(shù)F(gbesti)比較，若F(gbesti)>F(pbesti)，則更新gbest值。

(8)若滿足終止條件，則輸出全局最優(yōu)解gbesti，適應(yīng)度函數(shù)F(gbesti)的極小值點(diǎn)即為未知節(jié)點(diǎn)的最終定位坐標(biāo)。否則返回步驟(4)。

4 實(shí)驗(yàn)與仿真

4.1 實(shí)驗(yàn)環(huán)境和參數(shù)設(shè)置

為驗(yàn)證本文算法的有效性，本文基于Windows 10操作系統(tǒng)的MATLAB 2014平臺進(jìn)行仿真實(shí)驗(yàn)。本文試驗(yàn)場景設(shè)置為100 m×100 m的二維正方形區(qū)域，假設(shè)所有WSN網(wǎng)絡(luò)節(jié)點(diǎn)的通信半徑都為R。

免疫粒子群算法的初始化參數(shù)如表1所示。

表1 仿真參數(shù)

4.2 仿真分析

(1)信標(biāo)節(jié)點(diǎn)比例對定位精度的影響

假設(shè)通信半徑為30 m、節(jié)點(diǎn)總數(shù)為100，圖1給出信標(biāo)節(jié)點(diǎn)比例對定位精度的影響關(guān)系圖。從圖中可以看出，3種定位算法的平均定位誤差都隨著信標(biāo)節(jié)點(diǎn)的比例增加而減小。當(dāng)信標(biāo)節(jié)點(diǎn)比例相同時(shí)，本文算法的平均定位誤差與DV-Hop以及PSO-DV-Hop定位算法比較降低了15.03%、4.86%。另外，本文算法平均定位誤差曲線更平滑，表明其穩(wěn)定性更好。

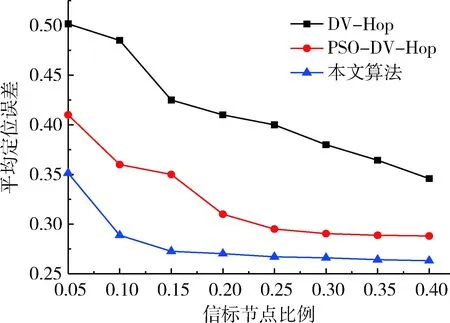
圖1 信標(biāo)節(jié)點(diǎn)比例與定位誤差關(guān)系圖

(2)通信半徑對定位精度的影響

假設(shè)節(jié)點(diǎn)總數(shù)為100時(shí)，信標(biāo)節(jié)點(diǎn)比例為10%，改變通信半徑進(jìn)行仿真，結(jié)果如圖2所示。從圖中可以看出，在通信半徑小于30 m時(shí)，3種定位算法的平均定位誤差都隨著通信半徑的增大而明顯減小，這是因?yàn)橥ㄐ虐霃降脑龃筇岣吡宋粗?jié)點(diǎn)與信標(biāo)節(jié)點(diǎn)的連通性，從而可以獲得更大范圍的信息交換來提高定位精度。但在通信半徑大于30 m時(shí)，平均定位誤差緩慢減小，趨于平滑，因此通信半徑并不是越大越好，通信半徑的增大也將提高通信開銷。另外，從3種算法對比可以看出，本文算法的定位誤差與經(jīng)典DV-Hop、PSO-DV-Hop定位算法相比，定位精度提高了13.27%、8.27%。

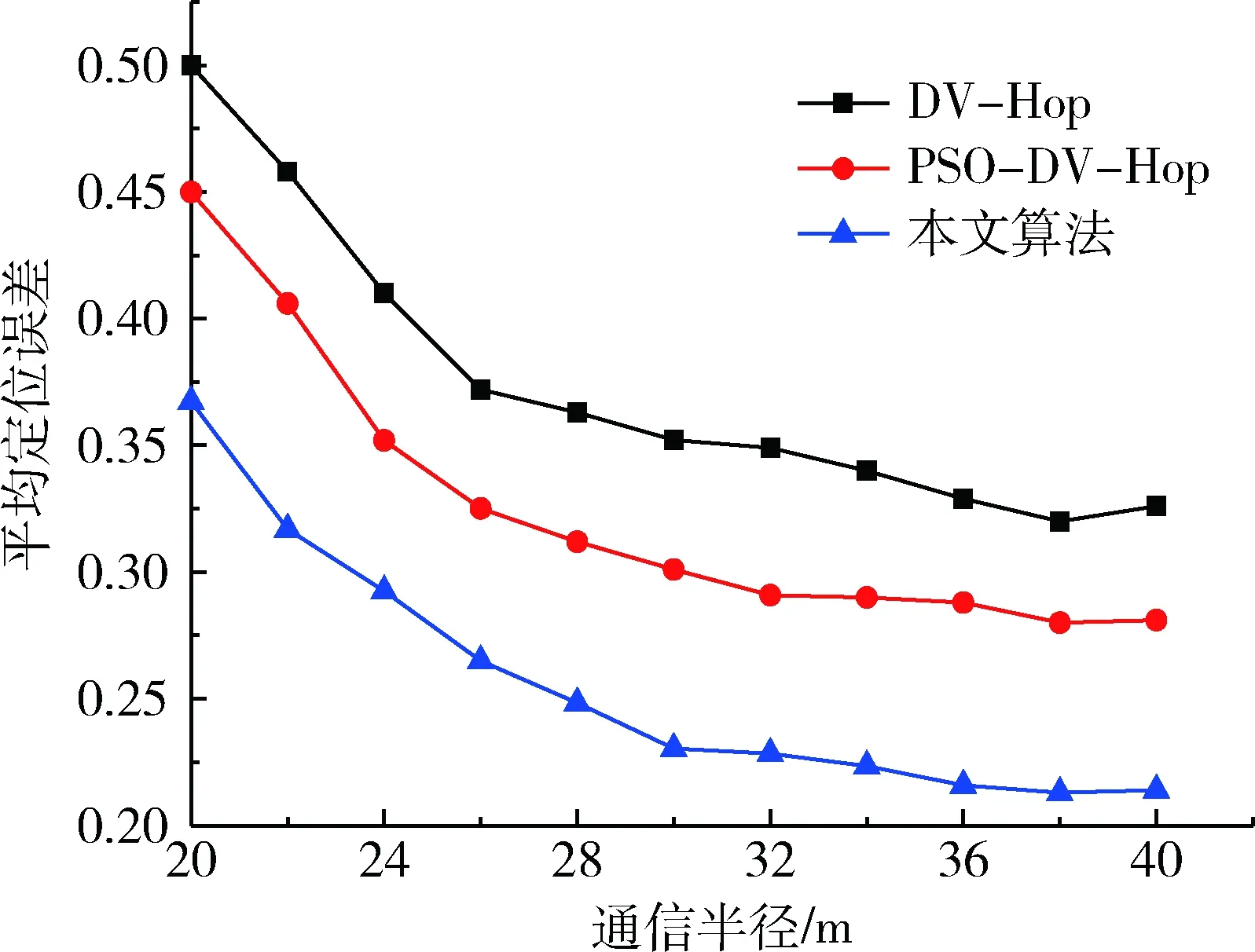
圖2 通信半徑與定位誤差關(guān)系圖

(3)節(jié)點(diǎn)總數(shù)對定位精度的影響

假設(shè)網(wǎng)絡(luò)節(jié)點(diǎn)的通信半徑為30 m時(shí)，信標(biāo)節(jié)點(diǎn)比例為10%，節(jié)點(diǎn)總數(shù)變化的仿真結(jié)果如圖3所示。從圖中可以看出，在通信半徑和信標(biāo)節(jié)點(diǎn)比例相同的情況下，節(jié)點(diǎn)的平均誤差隨著節(jié)點(diǎn)總數(shù)的增加而下降。隨著節(jié)點(diǎn)總數(shù)的變化，平均定位算法的變化幅度相對較大，這也反映了該算法的可擴(kuò)展性有待進(jìn)一步提高。但是，本文算法定位精度明顯優(yōu)于傳統(tǒng)的DV-Hop算法和PSO-DV-Hop算法，平均定位誤差分別降低了10.85%、5.89%。

圖3 節(jié)點(diǎn)總數(shù)與定位誤差關(guān)系圖

5 結(jié)論

本文闡述了典型DV-Hop定位算法的基本原理，分析了DV-Hop定位算法的誤差來源，并結(jié)合免疫粒子群優(yōu)化算法的特點(diǎn)，提出了一種免疫粒子群算法優(yōu)化的DV-Hop定位算法。在免疫粒子群算法中，通過調(diào)節(jié)機(jī)制使各適應(yīng)度的粒子維持一定濃度，保證群體的多樣性，克服粒子早熟，使得粒子快速收斂于全局最優(yōu)點(diǎn)，優(yōu)化待測節(jié)點(diǎn)位置坐標(biāo)。該算法在無需增加額外硬件設(shè)備的情況下，有效降低了定位誤差。但免疫粒子群算法的引入增加了算法復(fù)雜度，這將是下一步研究的重點(diǎn)。

參考文獻(xiàn)

[1] 錢志鴻, 孫大洋. 無線網(wǎng)絡(luò)定位綜述[J]. 計(jì)算機(jī)學(xué)報(bào), 2016, 39(6): 1237-1256.

[2] 于泉, 孫順遠(yuǎn), 徐保國, 等. 基于改進(jìn)粒子群算法的無線傳感器網(wǎng)絡(luò)節(jié)點(diǎn)定位[J].計(jì)算機(jī)應(yīng)用, 2015, 35(6): 1519-1522.

[3] FEI J.Optimization of immune particleswarm algorithmand application on wireless sensornetworks[J]. Computer Modeling & New Technologies,2014,18(11):1443-15448.

[4] 高美鳳, 李鳳超. 遺傳粒子群優(yōu)化的 DV-Hop 定位算法[J]. 傳感技術(shù)學(xué)報(bào), 2017, 30(7): 1083-1088.

[5] 王林,趙錦.一種基于誤差修正的改進(jìn)DV-Hop算法[J].計(jì)算機(jī)工程與應(yīng)用,2014,50(24): 109-112.

[6] TAO Q, ZHANG L. Enhancement of DV-Hop by weightedhopdistance[C]//Advanced Information Management, Communicates, Electronic and Automation Control Conference(IMCEC),2016 IEEE, 2016:1577-1580.

[7] 邴曉瑛,徐保國.基于改進(jìn)粒子群優(yōu)化的WSN定位算法[J]. 電子設(shè)計(jì)工程,2015，23(22): 143-146.

[8] 張超, 李擎, 王偉乾, 等. 基于自適應(yīng)搜索的免疫粒子群算法[J]. 工程科學(xué)學(xué)報(bào), 2017, 39(1): 125-132.

[9] 張曉, 范虹, 張莉, 等. 融入免疫思想的改進(jìn)型粒子群優(yōu)化算法[J].陜西師范大學(xué)學(xué)報(bào)(自然科學(xué)版),2017,45(3): 17-23.

[10] Jiao Wei,Cheng Weimin,Zhang Mei,et al. A simpleand effective immune particle swarm optimization algorithm[C]// International Conference in Swarm Intelligence. Springer, Berlin,Heidelberg, 2012: 489-496.

[11] He Xingshi, Han Lin. A novel binary differential evolution algorithm based on artificial immune system [C]// Evolutionary Computation,IEEE,2007: 2267-2272.