基于模糊PID的電動汽車用永磁同步電機(jī)矢量控制仿真研究

袁亞登，孟輝磊，馮乾隆，劉新亮

（長安大學(xué)汽車學(xué)院，陜西 西安 710064）

前言

近幾年，隨著環(huán)境污染的加重以及能源危機(jī)的出現(xiàn)，發(fā)展電動汽車成為了汽車工業(yè)的轉(zhuǎn)型方向。因此，對電動汽車驅(qū)動控制系統(tǒng)研究具有重大的理論和實際意義。永磁同步電機(jī)具有結(jié)構(gòu)簡單、功率密度高、制造成本低、過載能力強(qiáng)，低損耗、快響應(yīng)等優(yōu)點(diǎn)，在新能源汽車等領(lǐng)域得到了廣泛的應(yīng)用。目前存在許多永磁同步電機(jī)的控制算法，有PID控制、BP控制等，PID控制策略作為傳統(tǒng)控制領(lǐng)域最具代表性的一種控制策略，因其結(jié)構(gòu)簡單、控制精度高、控制性能穩(wěn)定等優(yōu)點(diǎn)，在各領(lǐng)域內(nèi)得到了應(yīng)用[1]。而對PMSM伺服控制系統(tǒng)，具有非線性的特性，特別是新能源汽車工況復(fù)雜，電機(jī)啟動頻繁，運(yùn)行環(huán)境多變，傳統(tǒng)的固定增益的PID控制器是一種線性控制策略，無法很好地滿足的永磁同步電機(jī)高精度、快響應(yīng)的控制要求，因此應(yīng)選取滿足其特點(diǎn)的控制策略。

目前，人們采用較多的是PID控制與其他控制策略結(jié)合，形成智能的復(fù)合控制策略，實現(xiàn)了對增益參數(shù)的智能校正，使電機(jī)伺服系統(tǒng)的魯棒性得到增強(qiáng)，從而獲得較好的控制效果，使電動汽車的穩(wěn)定響應(yīng)特性大大加強(qiáng)。模糊控制是一種典型的智能控制方法，對于參數(shù)的非線性變化有著較強(qiáng)的自適應(yīng)性。他的控制并不依賴于被控對象，同時也具有較高的控制精度本文對 PMSM 采取空間矢量的控制策略以及模糊控制與傳統(tǒng)PID控制相結(jié)合的控制算法，通過模糊控制對傳統(tǒng)PID控制的參數(shù)進(jìn)行自整定，并采用MATLAB 分別構(gòu)建傳統(tǒng)PID 控制模型與模糊PID閉環(huán)模型，通過對比兩種控制模式下永磁體同步電機(jī)的仿真結(jié)果，可知模糊PID控制模式下的永磁同步電機(jī)的性能得到了提升[2]。為實際控制系統(tǒng)的設(shè)計和實現(xiàn)提供了理論基礎(chǔ)和參考。

1 永磁同步電機(jī)d-q軸數(shù)學(xué)模型

在建立坐標(biāo)軸數(shù)學(xué)模型前，先做以下假設(shè)：①磁路為線性，忽略鐵心飽和；②忽略渦流和磁滯損耗；③磁場近似呈正弦分布，忽略邊端效應(yīng)；④氣隙分布均勻，磁回路與轉(zhuǎn)子位置無關(guān)，即各相繞組的電感與轉(zhuǎn)子的位置無關(guān)；⑤三相線圈繞組完全對稱，且各個參數(shù)均相同[3]。根據(jù)上述假設(shè)，以及永磁同步電機(jī)的物理模型，選取wm和iq（wm為轉(zhuǎn)子機(jī)械角速度）為狀態(tài)變量，并且采用id=0（iq，id分別為q，d軸電流）的矢量控制策略，這樣就得到簡化的三相永磁同步電機(jī)的動態(tài)數(shù)學(xué)模型如式（1）所示。

式中：P為微分算子；iq為q軸電流；wm為轉(zhuǎn)子機(jī)械角速度；R為定子電阻；Lq為電機(jī)q軸電感；φf為永磁體磁鏈；pn為電機(jī)極對數(shù)；B為摩擦系數(shù)；J為折算到電機(jī)主軸上的等效轉(zhuǎn)動慣量；uq為q軸電壓；TL為折算到電機(jī)主軸上的等效負(fù)載轉(zhuǎn)矩。因此，進(jìn)一步得到電機(jī)簡化模型的結(jié)構(gòu)，如圖1所示。

圖1 電機(jī)簡化模型結(jié)構(gòu)圖

2 PMSM矢量控制系統(tǒng)

在分析永磁同步電機(jī)d-q軸數(shù)學(xué)模型的基礎(chǔ)上，采用矢量控制策略，建立PMSM矢量控制系統(tǒng)如圖2所示。其中，SVPWM 為空間矢量脈寬調(diào)制。iq為轉(zhuǎn)矩電流、id=0為實際勵磁電流，該控制系統(tǒng)包含1個速度外環(huán)和2個電流內(nèi)環(huán)，電流環(huán)采用傳統(tǒng)的PID控制方式，為了增強(qiáng)系統(tǒng)的魯棒性及抗干擾能力，速度環(huán)則采用基于模糊PID 的控制器。從圖中可以看出，速度環(huán)經(jīng)過模糊自整定的PID控制器進(jìn)入電流環(huán)，電流環(huán)通過對直軸電流id和交軸電流iq的解耦控制，實現(xiàn)了電流分量的單獨(dú)控制，并最終實現(xiàn)轉(zhuǎn)矩控制的目的。

圖2 PMSM矢量控制系統(tǒng)

3 模糊PID控制器參數(shù)自整定

3.1 模糊PID控制器的基本原理

由于常規(guī)的PID控制器不具有在線調(diào)節(jié)參數(shù)的功能，無法滿足控制器參數(shù)在線自整定的要求。為了提高轉(zhuǎn)速外環(huán)的性能，本文將常規(guī)控制器與模糊PID控制理論相結(jié)合，將不同時刻輸出轉(zhuǎn)速與給定轉(zhuǎn)速的誤差e及誤差變化率ec為輸入變量，通過模糊處理器處理后，產(chǎn)生修正量△Kp、△Ki、△Kd通過式（2）對PID 的比例、積分、微分系數(shù)進(jìn)行修正，實時調(diào)節(jié)PID參數(shù)Kp，Ki，Kd，以適應(yīng)不同時刻的控制需求，其原理如圖4所示。

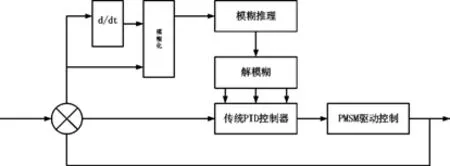
圖3 模糊PID控制器原理圖

其中Kp0，Ki0，Kd0為最初調(diào)整好的PID控制器參數(shù)。

3.2 輸入?yún)?shù)的模糊化及模糊集合的建立

設(shè)控制器的輸入量為x，范圍為，將該取值范圍稱為物理論域[4]。為了控制器設(shè)計以及后期修改的方便，通常將物理論域量化為離散論域進(jìn)行處理。如何選擇模糊控制器的輸入變量的量化因子和輸出控制量的比例因子非常重要。現(xiàn)將輸入誤差e和誤差變化率ec以及輸出量△Kp、△Ki、△Kd，都定義在離散論域（-3，3）上，則實際輸入值x與離散論域值b之間的換算關(guān)系可通過式（3）得出。

其中k為量化因子，這里k的取值為：

如果b不為整數(shù)，則按四舍五入取整，然后便可以將離散論域模糊化，將離散論域的每個值設(shè)置模糊集合，各模糊集合可設(shè)置為正大（PB）、正中(PM)、正小(PS)、零(ZE)、負(fù)小(NS)、負(fù)中(NM)、負(fù)大(NB)。設(shè)各輸入輸出均服從三角形隸屬度函數(shù)曲線，如圖4所示。

圖4 三角形隸屬度函數(shù)曲線圖

3.3 模糊控制規(guī)則的建立

在實際控制中，為了保證不同的偏差e和偏差變化率ec，系統(tǒng)會有較好的性能，需要根據(jù)一定的規(guī)則來調(diào)整PID的三個參數(shù)，基本規(guī)則如下：

（1）當(dāng)e很大時，系統(tǒng)應(yīng)取較大的比例系數(shù)Kp和較小的Kd加快系統(tǒng)的響應(yīng)。

（2）當(dāng)e中等大時，此時會有兩種情況出現(xiàn)：①若e和ec同號，被控量朝著偏離給定量的方向變化，為了使系統(tǒng)響應(yīng)具有較小的超調(diào)，Kp和Kd應(yīng)取得大一些，Ki應(yīng)取得適當(dāng)大；②若e和ec異號，被控量朝著接近給定值的方向變化，此時應(yīng)逐漸減小Kp，Ki和Kd。

表1 △Kp參數(shù)的模糊規(guī)則表

表2 △Ki參數(shù)的模糊規(guī)則表

表3 △Kd參數(shù)的模糊規(guī)則表

（3）當(dāng)e較小時，為了使系統(tǒng)有良好的穩(wěn)態(tài)性能，此時應(yīng)適當(dāng)弱化比例和微分的作用。并加強(qiáng)積分的作用，可以將Ki設(shè)為最大值。

根據(jù)上述規(guī)則，并進(jìn)行大量的實驗調(diào)試后，可以得到調(diào)整量△Kp，△Ki和△Kd的控制規(guī)則表，分別如表 1、表 2、表3所示。

3.4 模糊推理與輸出變量的解模糊化

根據(jù)量化后的e和ec，得到相應(yīng)的模糊變量[5]。再利用面積中心法則解模糊運(yùn)算得到相應(yīng)的PID的修正量△Kp、△Ki和△Kd，再根據(jù)式（2）計算出不同時刻系統(tǒng)需要的 PID參數(shù)需求，進(jìn)而使被控制的 PMSM 具有更好的動態(tài)與靜態(tài)性能[6]。

根據(jù)以上分析，在 MATLAB/Simulink仿真模型中，利用fuzzylogic工具箱建立模糊控制器如下圖所示。

圖5 模糊控制器設(shè)計圖

利用建好的模糊控制器，在 MATLAB/Simulink中建立模糊PID控制器，具體結(jié)構(gòu)圖如圖6所示。

圖6 模糊PID控制器模型

4 系統(tǒng)仿真及結(jié)果分析

4.1 仿真模型的建立

為了檢驗設(shè)計的合理性，根據(jù)建立的模糊PID控制器模型，在 MATLAB/Simulink環(huán)境下建立永磁同步電機(jī)空間矢量控制系統(tǒng)仿真模型如圖7所示。其中A、B、C分別為永磁同步電機(jī)的電源接口，g為逆變器信號控制端，m為電機(jī)的轉(zhuǎn)速轉(zhuǎn)矩等信號的輸出。ia，ib，

圖7 永磁同步電機(jī)空間矢量控制系統(tǒng)仿真圖

ic分別為永磁同步電機(jī)的定子電流[7]。

4.2 參數(shù)的設(shè)定

圖8 突加負(fù)載時轉(zhuǎn)速仿真實驗圖

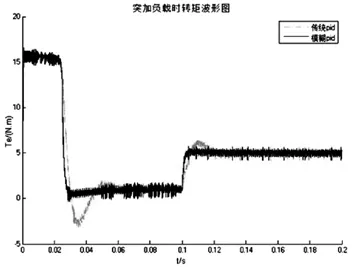
圖9 突加負(fù)載時轉(zhuǎn)距仿真實驗圖

系統(tǒng)中所用的電機(jī)額定功率P=10kW，額定轉(zhuǎn)矩T=50N.m，定子電阻R=0.22Ω，永磁體磁鏈，定子軸電感，定子轉(zhuǎn)動慣量J=0.006，電機(jī)極對數(shù)Pn=2，采樣周期TS=0.0000002s，逆變器直流母線電壓 Ud=380V，仿真時間設(shè)定為 0.2s，最大仿真步長設(shè)置為0.000001s，負(fù)載轉(zhuǎn)矩TL在0.1s時從1N·m突變到額定轉(zhuǎn)矩5N·m。得到電機(jī)轉(zhuǎn)速、轉(zhuǎn)矩與傳統(tǒng)PID控制對比如圖7、圖8所示。

對比圖8、圖9可知，與傳統(tǒng)PID相比，空載啟動時，模糊PID控制的調(diào)整時間從0.022s降低到0.018s，并且轉(zhuǎn)速無超調(diào)，轉(zhuǎn)矩幾乎無脈動，突加負(fù)載時，模糊PID控制的調(diào)整時間更短，轉(zhuǎn)速無超調(diào)且轉(zhuǎn)矩脈動很快衰減。

5 結(jié)論

本文針對永磁同步電機(jī)，提出了模糊控制與PID控制相結(jié)合的控制算法，并對其采用空間矢量控制策略分別建立了傳統(tǒng)PID和模糊PID的空間矢量的仿真模型，并對永磁同步電機(jī)突加負(fù)載時的響應(yīng)特性進(jìn)行了仿真研究，實驗結(jié)果表明，對于永磁同步電機(jī)，與PID控制相比，模糊自整定PID控制啟動平穩(wěn)、無太大的超調(diào)，有快的響應(yīng)特性，在突加負(fù)載時運(yùn)行較平穩(wěn)，幾乎沒有波動，魯棒性較強(qiáng)。表明基于模糊PID控制的永磁同步電機(jī)的矢量控制具有很好的動態(tài)特性。論文的研究為實際純電動汽車與電機(jī)驅(qū)動控制系統(tǒng)的分析與設(shè)計提供了新的思路，對我國電動汽車及驅(qū)動控制系統(tǒng)的開發(fā)具有很好的參考價值。

參考文獻(xiàn)

[1] 齊亮.基于滑模變結(jié)構(gòu)方法的永磁同步電機(jī)控制問題研究及應(yīng)用[D].上海:華東理工學(xué),2013.

[2] 姚振明,胡霞.基于MATLAB的永磁體同步電機(jī)模糊PID控制仿真[J].安徽理工大學(xué)學(xué)報,2016（6）.

[3] 袁登科,徐延?xùn)|,李秀濤.永磁同步電機(jī)變頻調(diào)速系統(tǒng)及其控制[M].機(jī)械工業(yè)出版社,2015:21-33.

[4] 劉杰,李允工,劉宇等.智能控制與 MATLAB 實用技術(shù)[M].科學(xué)出版社,2016:34-45.

[5] 李愛平,鄧海洋,徐立云等基于模糊的 PMSM 控制仿真研究[J].中國工程機(jī)械學(xué)報,2013(11).

[6] M.Abroshan,J.Milimonfared, and et al.An Optimal Control for Saturated Interior Permanent Magnet Linear Synchronous Motors Incorporating Field Weakening [C], 13th Power Electronics and Motion Control Conference, EPE-PEMC 008:1117-1122.

[7] 鮑建成.永磁同步電機(jī)PID參數(shù)優(yōu)化研究[J].計算機(jī)仿真,2012(04).