設計輔助齒抑制永磁同步直線電機端部效應

□ 張 弛 □ 湯廷孝 □ 鄧益民

寧波大學機械工程與力學學院 浙江寧波315211

1 概述

直線電機可以直接將電能轉化為機械能并輸出直線運動。直線電機的使用，簡化了機械傳動結構，由于其可靠性好、系統維護簡單，故在交通運輸、數控加工、物流傳送等領域都有應用［1］。永磁同步直線電機具有推力密度大、效率高、控制精度高、響應速度快等特點，在超精度加工領域前景廣闊。

然而，永磁同步直線電機也具有一定的局限性，由于直線電機鐵心前后端部和永磁體磁場相互作用產生磁阻力，磁阻力帶來端部推力和端部法向力，統稱為端部效應力。直線電機運動過程中，變化的端部效應力造成直線電機的機械振動，影響電機的工作精度和使用壽命。

針對這種情況，沈陽工業大學的彭斌等［2-3］提出采用端部V型結構的方法，減少磁阻力波動，并取得了較好的效果。一些學者［4-6］提出增加輔助極的方法，減少端部法向力波動，采用有限元法討論了不同尺寸端部輔助齒的影響，但沒有定量的分析。通過計算，推導出端部定位力最小值時，輔助極相關尺寸表達式。漢諾威大學的Jastrzembski等［7］提到在直線電機端齒部制造倒角的方法抑制推力波動。Kim等［8］提出電機端部采用弧形齒的方案，并且通過田口方法進行優化。然而，若此結構應用在初級鐵心上，過長的端部弧形齒顯然增加了電機的尺寸。朝鮮大學的Kim等［9］分析了階梯狀分布的端部輔助齒結構對端部效應力波動的影響。Jang等［10］從減少直線電機循環電流的角度出發，對電機端部進行結構優化。國內外許多學者通過圖解和公式計算對端部力進行了詳細的分析，得出端部推力波動可以分解為多個正弦或余弦波，并通過實驗進行驗證［11-13］。Wu Xiaoyan等［14］通過計算，對電機的整體尺寸進行優化，以減小推力波動、增加電機推力密度為目標，提出一種新型永磁同步電機。

目前，大多數關于直線電機端部效應力波動抑制的研究將端部力產生的波動簡化為正弦或余弦波，在此基礎上進行初級諧波或多級諧波的削弱［6，12］。但是，這樣的方法只能消除端部力波動中所占比例較大的波動，簡化的本身也會帶來誤差。

筆者提出的端部效應力削弱方案，考慮到在永磁同步直線電機實際工作時，由于永磁材料的非線性、鐵心磁導的變化等原因［15］，端部效應力表現為類正弦（余弦）形式［13，16-17］，提出端部添加多齒結構輔助齒來抑制力的波動。該方案具有很強的實用性，適用于多種永磁同步直線電機，且避免了大量的理論計算，結構簡單，便于加工。

2 端部效應力的數學建模

2.1 端部推力的分析

永磁同步直線電機的永磁體按照一定規律排列，在不同位置磁場分布存在差異，磁感線以極距τ為直徑或長軸，在平面上圍成圓或橢圓，如圖1所示，永磁體上的箭頭表示永磁體的充磁方向，動子鐵心在運動過程中，其端部所受磁阻力呈現周期性波動，且鐵心前后端推力的周期、振幅相同，方向相反。按照動子鐵心的移動方向，鐵心前端受力為正方向，后端為負方向，鐵心后端的推力總是阻礙電機的移動。

▲圖1 直線電機磁通示意圖

沿著電機移動方向，直線電機前端所受端部推力可以用傅里葉級數表示為［11］：

式中：F0為基準力；Fsn為sin函數表達的曲線波動力；Fcn為cos函數表達的曲線波動力；x為位移；Ft+為前端端部推力；Ft-為后端端部推力。

Δ=L-kτ，L為永磁同步直線電機的軸向長度，即動子鐵心的長度，k為整數，τ為極距。

將式（1）代入式（2），得直線電機后端端部推力：

從以上分析可知，永磁同步直線電機的前、后端端部推力波動均以極距τ為周期，波形為類正弦（余弦）波。通過改變直線電機軸向長度L，控制Δ的大小，使前后端部力在一定程度上相互抵消，達到抑制推力波動的目的。但是，為了確定Δ的值，需要進行大量的計算。

2.2 端部法向力的分析

直線電機端部法向力的波動不僅會給直線電機帶來振動和噪聲，還會在電機上產生力矩，給電機帶來俯仰運動的趨勢，在電機導軌產生附加的非線性摩擦力，影響電機穩定運行。因此，對于端部法向力的研究非常重要，下面通過對電機永磁體磁通的研究建立端部法向力相關力學公式。

由于永磁體產生的磁場在空間中按照一定規律分布，動子鐵心在變化的磁場中運動，產生變化的端部力。假設空氣和永磁體的磁導率相同，排列的永磁體產生穩定的磁場，磁感線以τ為周期呈圓形分布，如圖1所示。動子鐵心移動時，穿過法向端面的磁通可由磁通曲線 Φ（x）近似表示，將其傅里葉展開［13］：

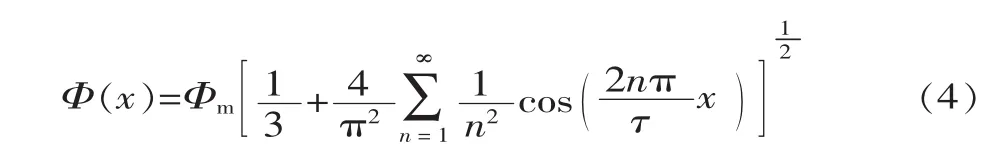
式中：Φm為經過動子鐵心邊緣磁通量的最大值。

在空間里，單位體積的磁場儲能wm可以表示為：

式中：B為磁感應強度；H為磁場強度；μ0為真空條件下的磁導率；Φ為經過動子鐵心縱向邊緣的磁通；S為磁感線在鐵心縱向表面所圍面積。

當動子鐵心經過一個極距長度τ時，氣隙磁場儲能發生了變化，儲能變化量為Wm：

式中：le為動子鐵心疊壓厚度；δ′為氣隙長度；V為氣隙體積；l1為經過鐵心縱向邊緣又返回永磁體的那部分磁感線在永磁體橫向所占的長度，l1=K1τ，K1為磁通壓縮系數。

聯立式（4）和式（6），氣隙儲能變化量Wm可表示為：

沿著動子鐵心運動的方向，動子鐵心前端所受端部法向力Ff+可表示為：

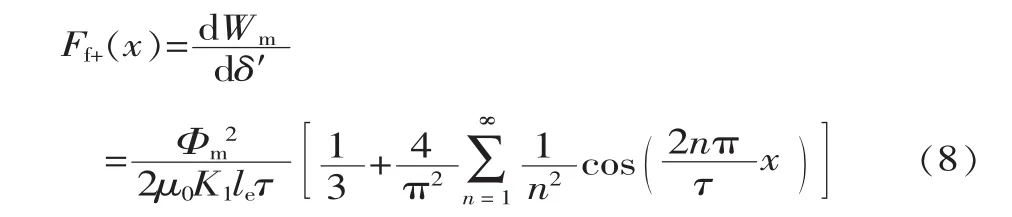
動子鐵心后端面的受力Ff-與之類似，可表示為：

通過分析可知，永磁同步直線電機前后端法向力波動僅初相位不同，波動同樣以極距τ為周期。對端部法向力和推力波動進行抑制時，若使Δ=τ/2，直線電機的前后端法向力大小相等、方向相反，可在最大程度上相互抵消；然而，方向相反的法向力位于電機前后端，產生力矩，會給電機運行帶來了新的問題。若使Δ=τ，則Ff+（x）=Ff-（x），直線電機前后端端部法向力同向，不會為電機帶來額外力矩，但同向端部力相互疊加后，合力的大小達到單邊力的兩倍，波動增加。

可見，通過調整電機橫向尺寸L來削弱端部法向力，存在著一定的局限性。

3 新型輔助齒抑制端部效應力

對于不同的永磁同步直線電機，在電機空載運行時，其力的波動波形不盡相同，但其端部法向力和端部推力都以極距τ作為周期，且波形規則。通過實際測試和仿真，永磁同步直線電機單端的端部推力和端部法向力波形圖近似如圖2和圖3所示［13］。

▲圖2 單端端部推力波動圖

▲圖3 單端端部法向力波動圖

永磁同步直線電機動子鐵心在移動時，在永磁體產生的磁場中受到磁阻力，這是端部力產生的根本原因。根據以上分析，可以確定端部推力和法向力的波動都遵循以極距τ為周期的規律，根據這一規律，結合端部效應力類似正弦（余弦）波的形式，如果永磁同步直線電機在移動過程中能產生多個僅初相位不同的波動力，且將這些波動力按照一定規律相互疊加，則可以相互抵消，從而有效抑制力的波動。

以圖2和圖3所示電機單端的端部推力和端部法向力波動為例，分析在一個極距τ內，初相位不同的力相互疊加對端部效應力波動的影響。

端部力波動疊加效應情況如表1所示。其中，n1條力的波動相互疊加時，相鄰波動之間的初相位差為τ/n1。為了更好地研究波動相互疊加后的情況，以波動因子KF為衡量標準進行研究：

式中：Fmax為波動力的最大值；Fmin為波動力的最小值；ΔF為n1=1時波動力的最大值與最小值差的絕對值。

表1 端部力波動疊加表

由表1可知，將端部波動力按照一定的方式進行疊加，可以有效抑制端部推力和端部法向力的波動，且在一個極距內，隨著端部力疊加的越多，力的波動越小。理論上，當端部效應力波動疊加到一定數量時，力的波動可以完全忽略不計。

對于端部推力波動，由于左右端的推力方向相反，電機前后端推力波動相互疊加后可以在一定程度上相互抵消。對于端部法向力波動，經過疊加后左右端部法向力波動減少，由于左右端力的方向相同，產生的力矩可忽略不計。經過疊加，力的恒定分量增大，端部法向力的恒定分量和電機導軌的支撐力能夠相互抵消。

基于以上分析，為了得到初相位不同的波動力，采用端部多齒結構，在直線電機端部制造多個平面，如圖4所示。為了避免齒與齒、齒與初級鐵心內部磁場相互耦合，齒與齒之間采用非鐵磁性材料連接。在運動過程中，每個輔助齒上產生的波動相互抵消，達到削弱端部力波動的效果。

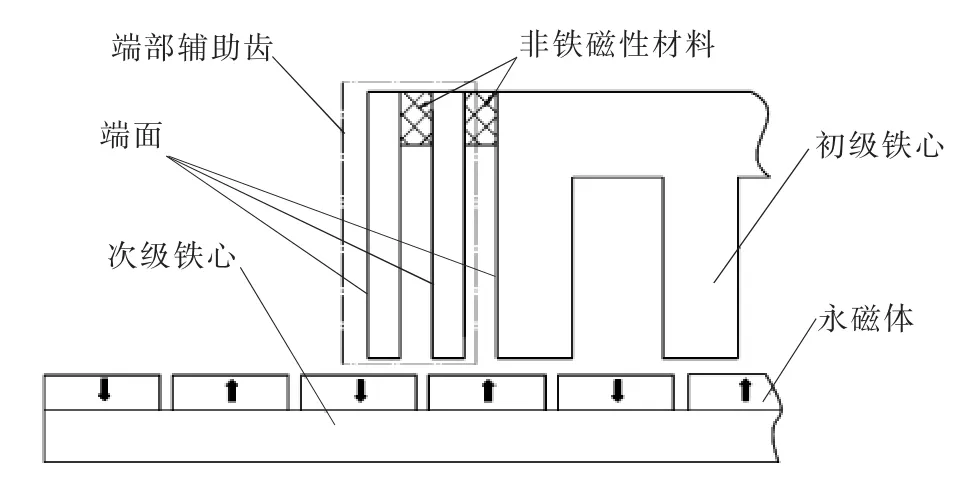
▲圖4 端部輔助齒示意圖

4 有限元驗證與分析

選擇12槽10極永磁同步直線電機進行有限元分析，為了研究直線電機端部效應力，并探究輔助齒的齒數和齒寬對端部力波動的影響，采用Maxwell仿真軟件。圖5為不帶輔助齒的直線電機，其相關參數見表2。

4.1 輔助齒數對端部效應力波動影響的仿真分析

▲圖5 永磁同步直線電機筒化結構

表2 不帶輔助齒的直線電機參數mm

利用有限元法，對輔助齒齒數由一到兩齒的永磁同步直線電機進行仿真，不帶輔助齒的直線電機作為對照。當齒數為N時，輔助齒和電機端部共產生N+1（n1=N+1）個端部平面，N+1個端部平面分布在長度為一個極距τ的范圍內，相鄰齒平面相距τ/（2+N），本次仿真中，輔助齒厚hf為6 mm。輔助齒材料與動子鐵心相同。

在永磁同步直線電機的瞬態仿真中，電機運行距離為2τ，端部效應力仿真結果如圖6和圖7所示（對于端部法向力波動，為了研究方便，仿真結果減去了一個恒定分量，每個波動中，最小值點相同）。

從圖6和圖7中可以看出，在無輔助齒時，端部推力和端部法向力波動均呈周期性變化，在兩個極距內波動了兩次，說明電機的推力波動的確以極距τ為周期。

當輔助齒齒數由零增加至二時，電機波動幅值隨著齒數的增加，即端部平面的增加而下降，一齒和兩齒時永磁同步直線電機的端部推力波動因子KF1分別為59.3%和22.4%，和上文波動力疊加后波動因子變化結果基本相同。此外，在端部一齒時，端部推力波動的波峰和波谷下凹和上凸，表現出疊加的特征。在端部兩齒時，周期由τ變為近似的τ/3，符合力的波動相互疊加后的結果。可見，通過使用多齒結構制造端部平面的方法，可以使多組波動力相互疊加并相互抵消，有效抑制永磁同步直線電機的端部推力波動。

然而，值得注意的是，一齒和兩齒時永磁同步直線電機的端部法向力波動因子KF2分別為82.46%和73.6%，且端部法向力的周期基本不變。采用端部多齒結構，可以在一定程度上抑制端部法向力，但端部輔助齒齒數的變化，不改變法向力的周期。

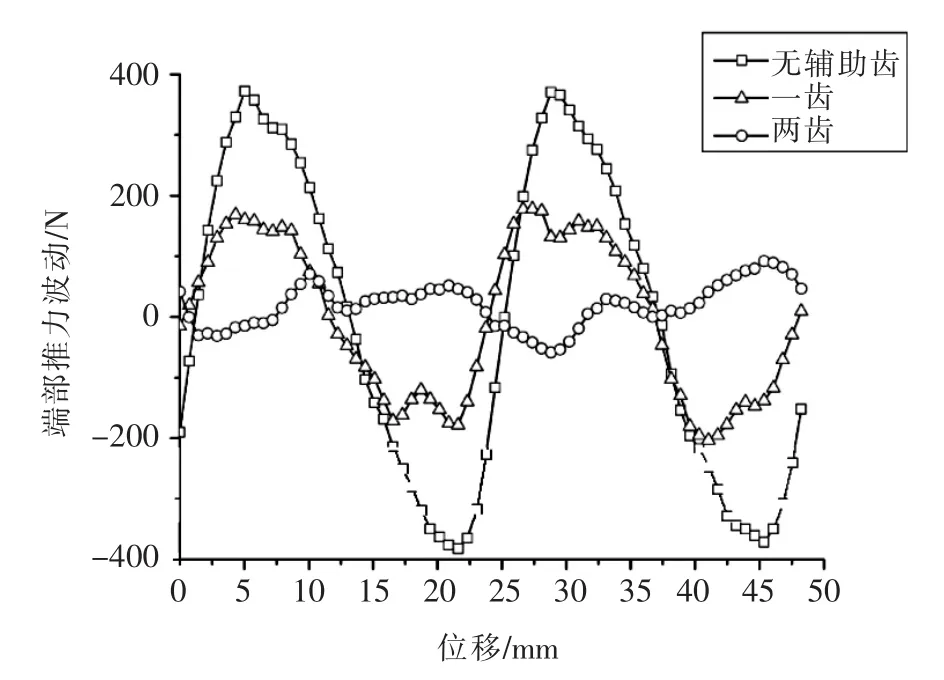
▲圖6 直線電機端部推力波動圖

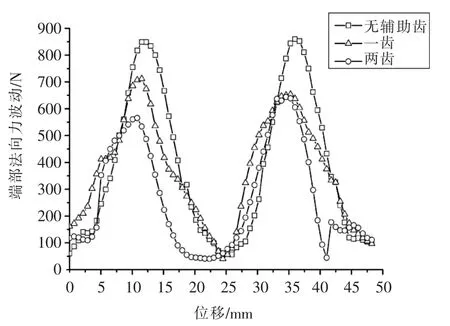
▲圖7 直線電機端部法向力波動圖

本次仿真中僅僅考慮一齒、兩齒時電機的端部效應力，因為在一個極距范圍內，隨著齒數的增加，齒與齒之間的距離減少，彼此之間磁場相互干擾，導致輔助齒磁場的分布發生變化。圖8為輔助齒厚為4 mm時，不同輔助齒的磁通密度分布圖，當電機在如圖所示的位置時，相比于端部輔助齒齒數為一和二，在齒數為三的情況下，最內側輔助齒周圍磁場幾乎被隔絕，導致其無法產生產生足夠的磁阻力，影響輔助齒對波動力的抑制。

▲圖8 端部輔助齒磁通密度分布圖

在本例中，為了防止輔助齒之間相互干擾，當端部輔助齒齒數為二時，對永磁同步直線電機端部效應力波動的抑制最佳。

4.2 輔助齒厚度對端部效應力波動影響的仿真分析

探究輔助齒厚hf對端部效應力波動的影響，在端部輔助齒齒數為二的基礎上，進一步優化分析。圖9和圖10為輔助齒齒厚hf由3 mm變化到7 mm時，永磁同步直線電機的端部推力和端部法向力波動情況。

由圖9和圖10可知，當電機輔助齒厚度改變時，端部推力波動周期和振幅變化，端部法向力波動的周期基本不變，振幅改變，這說明輔助齒的厚度對推力波動的周期和振幅影響較大，但僅對法向力波動的振幅產生影響。

由圖9和圖10還可以看出，從輔助齒齒厚4 mm開始，隨著齒厚的增加，端部推力波動和端部法向力波動的幅值逐漸減小；當輔助齒厚度在5～6 mm時，端部效應力波動最小。其中，當齒厚為6 mm時，端部推力波動正反向峰值最小；當齒厚為5 mm時，端部法向力波動正反向峰值最小，之后，隨著齒厚的增加，力的波動增加。

對仿真結果進行分析，當齒厚較小時，端部輔助齒極易發生磁飽和，其對端部力的抑制作用較弱。當齒厚較大時，由于齒與齒之間的間隔太小，彼此之間磁場相互影響，如圖11所示。隨著輔助齒齒厚的增大，相鄰齒之間的磁力線明顯增加。輔助齒周圍磁場分布發生較大的變化，導致端部力波動增加。

根據以上分析，在本例中，當輔助齒厚度在5～6 mm，對永磁同步直線電機端部法向力波動的抑制達到最佳。

5 結束語

通過理論分析和有限元仿真，提出了一種抑制永磁同步直線電機端部效應力波動的方法，并得到了如下的結論。

（1）通過理論分析，建立端部推力和端部法向力的數學模型，進一步得出永磁同步直線電機端部力的波動均以極距τ為周期。結合分析計算，提出采用端部多齒結構，制造多個端部平面，產生多組波動力，其相互疊加能夠有效抑制力的波動。

（2）通過有限元仿真分析，證明了多齒結構對端部效應力波動的抑制能力。得出輔助齒厚度影響端部推力波動幅值和周期，僅影響端部法向力波動幅值的結論，并對輔助齒厚進行優化。

▲圖9 不同齒厚端部推力波動比較圖

▲圖10 不同齒厚端部法向力波動比較圖

▲圖11 端部輔助齒磁力線分布圖