平均間隙法的一種改進算法

滕煥樂 聶虎嘯 劉成龍

(1.中鐵第四勘察設計院集團有限公司，湖北武漢 430063；2.中國鐵路設計集團有限公司，天津 300142；3.西南交通大學地球科學與環境工程學院，四川成都 610031)

變形監測網穩定性分析的基準點一般應遠離變形體且地質情況穩定[1，4]，這樣可以保證每次測量都能得到監測點相對于同一個位置基準的位移量。理論上，根據基準點提供的固定位置基準解算監測點的變形量是可靠的，然而由于多種原因，基準點也有可能發生位移，如果仍然采用發生位移的基準點進行測量與平差，則不能準確地反映形變發生的實際情況，從而得出錯誤的變形分析結果和結論。因此，在變形監測網平差計算之前，對變形監測基準點進行穩定性分析至關重要。

目前，對變形監測網進行穩定性分析的主要方法有t檢驗法、平均間隙法等。t檢驗法適用于圖形簡單、點數較少的監測網[2]。平均間隙法的應用則更廣，常用于監測網穩定性的顯著性檢驗。

1 平均間隙法的傳統算法

1.1 整體檢驗

平均間隙法是變形監測網穩定性分析的一種常用方法。首先通過整體檢驗，對變形監測網的穩定情況進行判斷，若判斷結果顯示網中無動點，則穩定性分析結束；反之，則應通過后續的不穩定點搜索找出網中的動點。

1.2 不穩定點搜索

若整體檢驗沒有通過，則意味著網中存在不穩定點，需要找出這些不穩定點。首先將網中所有點分為穩定點F組和不穩定點M組，同時將坐標間隙ΔX以及間隙的權陣PΔX分組，具體分組方法如下[6]

(1)

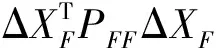
(2)

由此獲得

(3)

令

(4)

則F組點穩定性檢驗的統計量為

(5)

式中，μ2為兩期觀測的聯合單位權方差，其自由度為f。

若F1F(fF，f)，則F組中含有不穩定點。

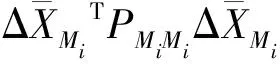
1.3 傳統算法的不足

(1)過程復雜計算量大

在進行過一次搜索后，之后的每次搜索計算，需要提取至少兩個點的間隙權陣信息，該項工作較提取一個點的間隙權陣復雜，且計算量較大，影響穩定性分析的效率。

(2)數據重復使用

傳統做法是將已搜索出的不穩定點再次納入不穩定點組，進行其他不穩定點的搜索，數據重復使用。

(3)循環性不強編程計算較為復雜

平均間隙法的傳統算法循環性不強，按照其算法原理進行編程計算較為復雜，影響算法效率。

2 平均間隙法的改進算法

2.1 不穩定點的搜索

利用傳統算法進行第一次搜索后，確定監測網的t個點中第i點為可能的不穩定點，改進后的方法是不再將i點納入第二次及之后搜索的不穩定點組中，而是剔除i點，將剩余的t-1個點視為整體。依次將t-1個點作為不穩定點組，計算其不穩定性指標，將其中最大的點視為不穩定點，然后再檢驗其余點所構成網的圖形一致性。若第二次搜索后其余點的圖形一致性通過檢驗，則穩定性檢驗結束。若未通過檢驗，則需要進行第三次甚至更多次的搜索。第三次及之后的搜索與第二次搜索一樣，亦不考慮已搜索出的不穩定點，其搜索過程與傳統算法的第一次搜索一致，每搜索出一個動點后就對剩余的點進行圖形一致性的檢驗。重復上述過程，直到剩余的點均穩定為止。

2.2 改進算法的優勢

從上述改進算法中可以看出，改進后的算法較傳統算法簡單、計算量小、循環性強，有利于提高編程和計算的效率，更適用于監測網的穩定性分析。

3 設計與算例分析

共選取了8個點，構成一個高鐵的沉降監測網。網中有3個基準點(BM1、BM2、BM3)和5個監測點(1～5號點)，對該網進行兩個周期的沉降監測。在第二期測量時，將基準點中的BM3點抬升2 mm左右，將監測點中的3號點下降3 mm左右，以達到驗證穩定性分析結果的目的。具體網形設計如圖1所示。

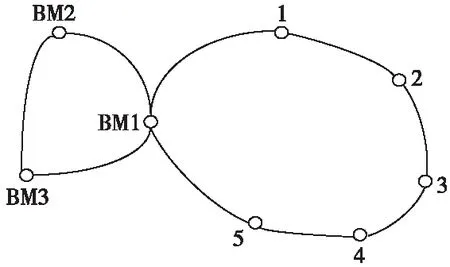
圖1 計算實驗設計的沉降監測網

3.1 第一部分實驗

仿真設計監測網兩期觀測資料如表1所示。

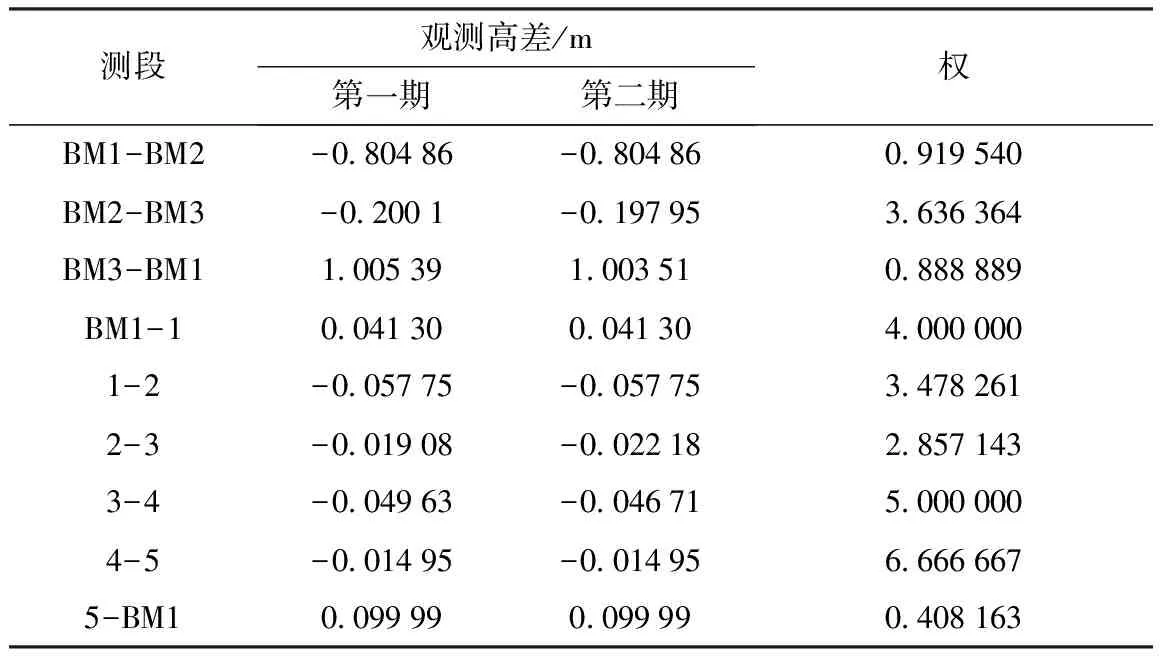
表1 沉降監測網的兩期觀測資料

(1)平均間隙法傳統算法

兩期監測網經自由網平差后，結果如表2所示。

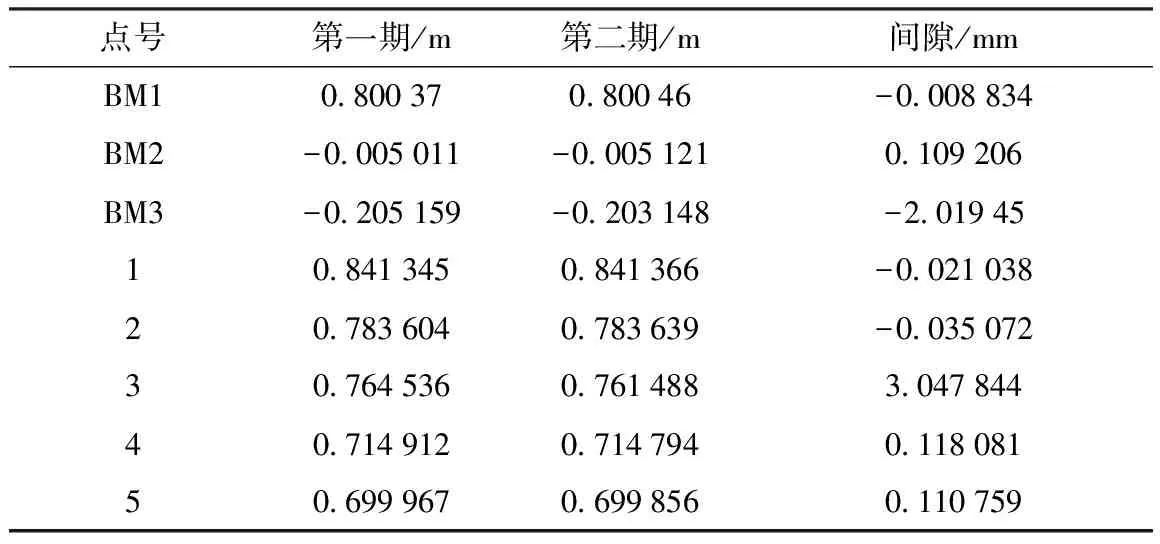
表2 兩期監測網自由網平差結果

①整體檢驗

根據兩周期觀測資料秩虧自由網平差結果，求得的間隙及其權陣如下

ΔX=(-0.008 834，0.109 206，-2.010 945，-0.021 038，-0.035 072,3.047 844,0.118 081,0.110 759)T

(6)

兩期觀測平差后，聯合方差估值為

(7)

假設兩次觀測監測點沒有變動，則可計算聯合方差估值

(8)

構造F檢驗統計量

(9)

檢驗沒有通過，故應認為網中存在不穩定點。

②不穩定點的搜索

分別將網中的點看做動點，計算8個點的圖形不一致性指標，結果如表3所示。

表3 各點圖形不一致性指標

注：若點的圖形不一致性指標<10-5，取0。

對剩余的點重新構成統計量，進行穩定性整體檢驗

(10)

F檢驗沒有通過，需繼續進行不穩定點搜索。將剩余的7個點與不穩定點3組成不穩定點組，計算7個不穩定點組的圖形不一致性指標，計算結果見表4。

經比較發現，BM3點和3號點構成的不穩定點組的圖形不一致性指標最大，故懷疑BM3點發生變動。同時剔除3號點和BM3點，計算剩余點的圖形一致性指標，并做整體檢驗

表4 各點組圖形不一致性指標

(11)

剩余點通過檢驗，由此認為網中除了3號點和BM3點外，其余的點均為穩定點。

③穩定性分析結果

網中3號點和BM3點發生變動，其余點均未發生變動，與實驗設計結果一致。

(2)平均間隙法的改進算法

①不穩定點搜索

在確定3號點為不穩定后，將剩余7個點重復第一次搜索過程。過程如下：

將剩余7個點依次看做動點，作為不穩定點組，分別計算7個點圖形不一致性指標，結果如表5所示。

表5 各點的圖形不一致性指標

經比較發現，BM3點的圖形不一致性指標最大，故懷疑BM3點發生變動。剔除BM3點，對剩余6個點做整體檢驗

(12)

剩余6個點通過檢驗，由此認為網中除了3號點和BM3點，其余的點均未發生變動。

②穩定性分析結果

經過檢驗，認為網中3號點和BM3點發生變動，其余點均未發生變動，與實驗設計結果一致。

(3)兩種方法的穩定性分析結果比較

上述兩種不同穩定性分析方法的檢驗結果均顯示，整個沉降監測網中BM3點和3號點發生變動，與試驗設計相符。

3.2 第二部分實驗

(1)對基準點進行穩定性分析

根據兩周期觀測資料，首先對基準網進行秩虧自由網平差，求得各點間隙及其權陣

(13)

經整體檢驗，網中存在不穩定點。

分別將網中的點看做動點，計算3個點的圖形不一致性指標，結果如表6所示。

表6 各基準點的圖形不一致性指標

(14)

通過檢驗，由此認為，基準點中只有BM3點為不穩定點。

(2)對監測點進行經典自由網平差及穩定性分析

通過上述計算確定基準點中BM3點為不穩定點，剔除BM3點，將兩次基準點秩虧自由網平差得到的BM1點高程的均值作為經典自由網平差的起算數據，對兩期觀測數據進行經典自由網平差。平差后，各監測點的間隙及其權陣如下

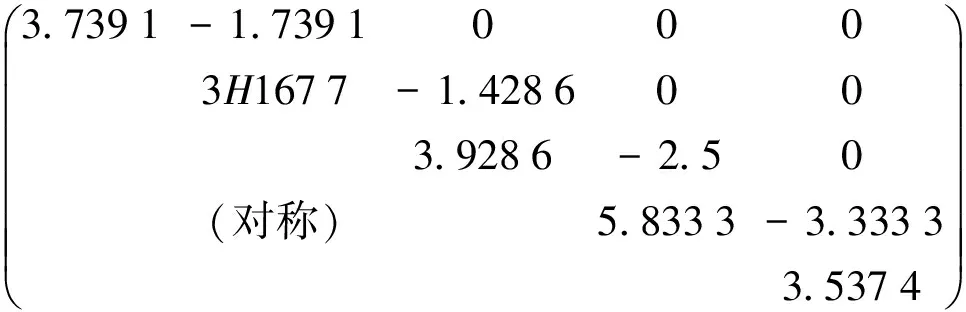
(15)

經整體檢驗，網中存在不穩定點。

分別將網中的點看做動點，計算5個點的圖形不一致性指標，結果如表7所示。

表7 各監測點的圖形不一致性指標

對剩余的點重新構成統計量，做整體檢驗

(16)

通過F檢驗，證明只有3號點不穩定。

(3)穩定性分析結果

結合上述(1)、(2)步的計算，檢驗出全網中BM3點和3號點為不穩定點，其余點均未發生變動，與試驗設計一致。

4 結論

(1)無論是采用平均間隙法的傳統算法，還是采用本文提出的改進算法，均可以對沉降監測網進行穩定性分析。改進算法的計算過程更為簡單，條理更清晰。

(2)計算試驗的第一部分中，將基準點與監測點一起進行穩定性分析，并且得到了與實驗設計一致的結果，由此說明，平均間隙法可同時對基準點和監測點進行穩定性分析。

(3)計算試驗的第二部分中，在對基準點進行穩定性分析后，利用穩定的基準點對監測點進行經典自由網平差，并利用平差結果進行監測點的穩定性分析，得到的結果與試驗設計相符。由此說明，當監測網中有穩定的基準點時，可以對精測網進行經典自由網平差，再利用平均間隙法對監測網進行穩定性分析，算法更為簡單。

[1] 楊學超，楊彩平.平均間隙法和單點檢驗在變形監測網中的應用[J].蘭州交通大學學報，2011，30(6):30-32

[2] 韓易，黃騰，沈月千，等.基于改進平均間隙法的狹長區域平面控制網穩定性檢驗[J].水利與工程技術學報，2013(4):164-167

[3] 尹暉，楊睿，陳鵬云.監測網基準點穩定性檢驗方法與應用[J].武漢理工大學學報，2012，32(6):861-864

[4] 黃聲享，尹暉，蔣征.變形監測數據處理[M].武漢:武漢大學出版社，2010

[5] 陶本藻.自由網平差與變形分析[M].北京:測繪出版社，1984

[6] 黃立人.用于相對穩定點組判別的QUAD法[J].大地測量與地球動力學，2002(2):10-15

[7] 滕松，張鐸強，周照明，等.網形不一致的工程控制網穩定性分析[J].測繪工程，2009，18(2):59-62

[8] 陳剛，張軍，等.地鐵沉降監測網穩定性分析與探討[J].測繪通報，2012(12):25-29

[9] 吳杰，余騰，潘慶林.工程控制網的穩定性研究[J].測繪科學，2011，36(5):31-33