極限狀態法與容許應力法鐵路大跨連續梁設計對比分析

閆 巖

(中鐵第一勘察設計院集團有限公司，西安 710043)

1 概述

當前，我國鐵路橋涵規范的計算理論采用的是容許應力法，而工民建、公路、市政等行業，乃至國外的橋涵結構領域均采用以可靠度理論為基礎的極限狀態法，為適應鐵路橋涵技術的不斷發展，實現與國際接軌，進一步提高設計水平，規范的計算理論從容許應力法向極限狀態法轉軌是十分必要的[1]。

中國鐵路總公司于2014年發布了《鐵路橋涵極限狀態法設計暫行規范》(Q/CR9300—2014)[2](以下簡稱為“《暫規》”)，并于2016年開展了鐵路橋涵極限狀態法試設計工作[1]，筆者通過參與本次試設計工作，以黔張常鐵路某主跨100 m連續梁為例，采用《暫規》和鐵路橋涵設計系列規范[3-4](以下簡稱為“《現規》”)進行計算對比分析，驗證《暫規》的合理、可行性。

2 設計資料

2.1 主要技術標準

(1)鐵路等級：Ⅰ級。

(2)正線數目：雙線。

(3)設計速度：200 km/h。

(4)軌道類型：有砟軌道。

(5)線間距：5.0 m。

(6)設計活載：中-活載。

(7)直曲線：曲線半徑4 504.6 m。

2.2 結構尺寸及單元劃分

本次計算采用的梁體為變高度變截面箱梁，一聯總長221.5 m，邊支座中心至梁端距離0.75 m，計算跨度為(60+100+60) m，箱梁截面采用單箱單室直腹板，邊支點及跨中梁高為4.3 m，中支點梁高7.3 m，梁底變化段曲線采用二次拋物線。箱梁頂寬為12 m，底寬6.7 m。頂板厚0.4 m，底板厚0.5～1.0 m，腹板厚0.5～0.9 m，中支座中心橫向間距為5.7 m，邊支座橫向間距為5.5 m,,中支點處橫隔梁厚3.0 m，邊支點橫隔梁厚1.6 m。

本連續梁為對稱結構，以下結果分析時選取其一半結構的計算分析，半跨結構劃分為34個節點，極限狀態法進行手算，容許應力法計算采用有限元軟件進行分析，為便于比較，兩種方法采用相同的結構尺寸及配束，梁體半跨立面見圖1，單元劃分見圖2，橋梁典型斷面見圖3、圖4。

圖1 (60+100+60) m連續梁半跨立面(單位： cm)

圖2 半跨連續梁節點單元劃分

圖3 中跨支點橫截面(單位：cm)

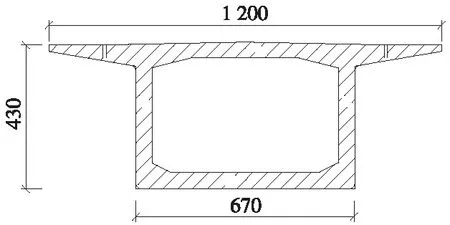
圖4 中跨跨中橫截面(單位：cm)

2.3 設計荷載

(1)結構自重G1：材料容重按《暫規》[2]第4.2.1條采用，預應力混凝土結構取26.5 kN/m3。

(2)結構附加恒載G2(線路設備及人行道等)：采用有砟橋面，包括鋼軌、道砟、軌枕、防水層、保護層、人行道、擋砟墻、聲屏障、電纜等附屬設施自重。二期恒載總計201 kN/m。

(3)沉降：考慮支座沉降0.01 m。

(4)列車活載及其動力效應：《暫規》的動力系數

《現規》的動力系數

(5)溫度荷載：考慮升溫20 ℃，降溫25 ℃，溫差考慮頂板升溫5 ℃。

2.4 建筑材料及配束情況

混凝土強度等級C55，預應力鋼束為外徑15.7 mm標準型鋼絞線，中支點配置48根頂板束和34根腹板束，中跨跨中配置36根底板束，邊跨跨中配置16根底板束，計算考慮1根φ32 mm豎向預應力鋼筋。

3 對比分析

3.1 正截面抗彎強度對比

抗彎強度是判定梁式結構是否安全的重要指標之一，對于連續梁，通常以外荷載引起的跨中正彎矩和支點處的負彎矩作為控制因素，用以查看梁體是否能夠承受彎矩而不發生彎曲破壞。

3.1.1 兩種方法計算采用的方法

《暫規》[2]和《現規》[4]在計算正截面抗彎強度時的公式原理是一樣的，不同的是兩套理論的材料強度取值不同，且極限狀態法采用荷載分項系數的方法表達荷載效應，見式(1)，而容許應力法采用安全系數的方法評價強度，見式(2)

Sd≤Md

(1)

K·M≤Md

(2)

式(1)中，公式左邊為荷載效應，公式右邊為結構抗力；式(2)中，K為安全系數，主力時，K=2.2，主力+附加力時，K=1.98。

可以看出，由于荷載組合的計算方法和材料強度的取值不同，極限狀態法和容許應力法對于正截面抗彎強度安全系數的計算結果是有差異的，兩種方法計算出來的安全系數無法直接進行比較，故采用安全儲備“(安全系數-限值)/限值”來進行評定。

3.1.2 兩種方法對比分析

為對應容許應力法的主力組合和主+附組合，極限狀態法采用作用效應的基本組合1和基本組合4。

正截面抗彎強度的對比結果如圖5和圖6所示。

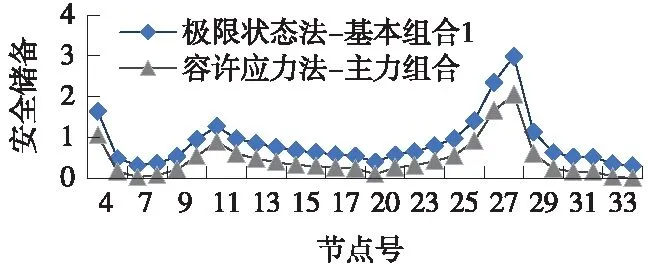
圖5 正截面抗彎強度安全儲備對比(主力組合)

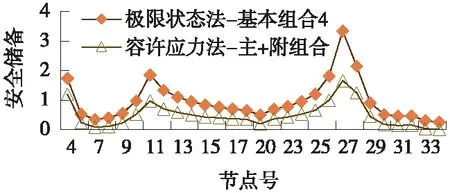
圖6 正截面抗彎強度安全儲備對比(主+附組合)

由圖5、圖6可以看出，兩種方法計算得到的安全儲備，在連續梁上各截面的趨勢是一致的，邊跨支點附近、中跨支點、中跨跨中均為控制截面，安全儲備較低，但滿足規范要求。

無論是主力組合還是主+附組合，極限狀態法的正截面抗彎強度安全儲備都要稍大于容許應力法，原因也在于兩者在材料強度的取值上有所不同。

3.2 正截面抗裂性對比

結構的抗裂性是評價結構安全性能重要指標之一，梁式結構往往通過正截面的抗裂性能來掌握結構抵抗開裂的能力。

3.2.1 兩種方法計算采用的方法

計算抗裂性，極限狀態法采用的荷載組合是正常使用極限狀態的頻遇組合和準永久組合，《暫規》[2]中規定了這兩種組合中荷載的組合值系數均為1，也就說明對于荷載效應來講，極限狀態法和容許應力法計算的結果應當是一樣的，不同之處在于兩者的結構抗力表達公式，即評價抗裂性的方式不一樣。

《暫規》[2]7.5.17-1條，對不容許出現拉應力的預應力混凝土構件，由預加力引起的受拉區邊緣混凝土的預壓應力應大于或等于由荷載效應頻遇、準永久組合作用下受拉區邊緣混凝土的拉應力。即

σct≤σcp

《現規》[4]6.3.9-1條對于受彎構件抗裂性由下列公式計算

Kf·σ≤σc+γfct

式中，Kf為抗裂安全系數，主力和主+附組合時，Kf=1.2。

由于抗裂安全系數的表達方式不同，無法直接進行比較，還是采用安全儲備的方式進行評定。

3.2.2 兩種方法對比分析

為對應容許應力法的主力組合和主+附組合，極限狀態法采用作用效應的頻遇組合4和頻遇組合7。

由圖7、圖8可以看出，主力組合時，對于中跨支點兩側的截面，兩種方法的安全儲備基本一致，在靠近中跨支點1/4處和邊跨支點1/4處，極限狀態法的安全儲備明顯高于容許應力法，但是在節點9處，極限狀態法的安全儲備為0。對于主+附組合，安全儲備曲線的趨勢與主力組合剛好相反，中跨支點兩側的截面極限狀態法明顯高于容許應力法。

出現以上趨勢的原因在于兩種方法判定正截面抗裂性的方式不一樣，但兩種方法計算得到的正截面抗裂性安全儲備曲線的總體趨勢大致是一樣的。

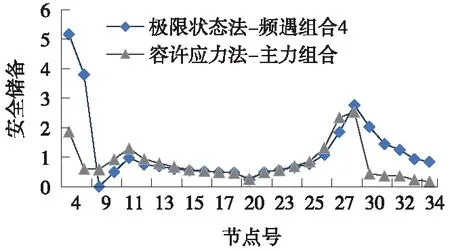
圖7 正截面抗裂性安全儲備對比(主力組合)

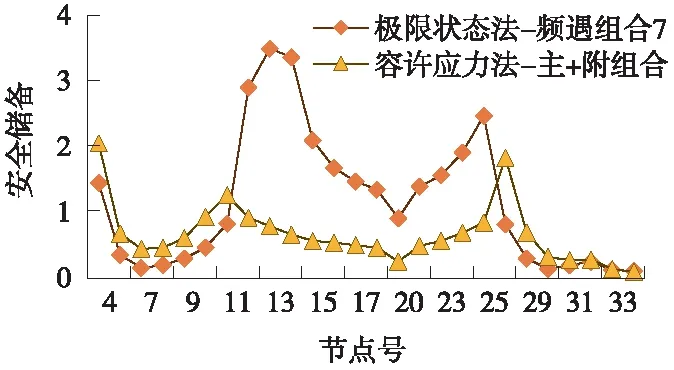
圖8 正截面抗裂性安全儲備對比(主+附組合)

3.3 斜截面主拉應力對比

同正截面抗裂性一樣，主拉應力作為評價結構斜截面抗裂性的控制因素，也是評價結構安全性能重要指標之一。

3.3.1 兩種方法計算采用的方法

《暫規》[2]和《現規》[4]計算主拉應力時的公式原理是一樣的，不同之處在于容許應力法計算法向壓應力和剪應力時考慮了1.2的安全系數。

《暫規》[2]7.5.19條計算主拉應力公式

τ0=τ-τpv

而《現規》[4]中計算公式

τ0=Kf1τ-τpv

式中對不允許出現拉應力的結構Kf1=1.2

3.3.2 兩種方法對比分析

為對應容許應力法的主力組合和主+附組合，極限狀態法采用作用效應的頻遇組合5和頻遇組合9，并摘取換算截面重心處的主應力，負號代表截面受拉。

從圖9、圖10可以看出，計算主拉應力時，無論是主力組合還是主+附組合，曲線趨勢是一致的，最大主拉應力出現在邊跨支點和中跨支點的位置，而由于容許應力法在計算中考慮了1.2的安全系數，導致主拉應力計算結果偏大。

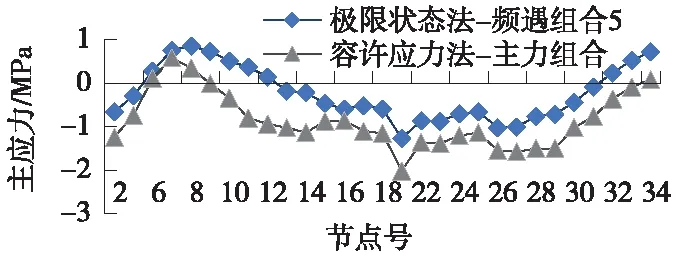
圖9 斜截面主拉應力對比(主力組合)

圖10 斜截面主拉應力對比(主+附組合)

對于兩種方法判定斜截面抗裂性的公式也不一樣，《暫規》[2]7.5.18條檢算斜截面抗裂性的公式

γcd·σtp≤fctk

其中對于分項系數γcd取1.5。而《現規》中檢算斜截面抗裂性是沒有分項系數的，即主拉應力不能超過材料極限抗拉強度

τtp≤fct

由于本次計算的連續梁采用懸灌法施工，對于分段施工結構，《現規》[4]中已說明應考慮拼接縫處抗裂性的降低，降低值應根據試驗確定。而《暫規》[2]中未對因施工方法不同需考慮拼接縫抗裂性降低的說明或規定，故而兩種方法判定斜截面抗裂性的基準和原則不一樣，關于此點，建議《暫規》[2]在修訂的過程中增加因施工方法不同而導致拼接縫處抗裂性降低的說明。

4 結論

采用極限狀態法和容許應力法，對主跨100 m連續梁的正截面抗彎強度、正截面抗裂性和斜截面抗裂性進行了對比分析，得出以下結論。

(1)對于主跨100 m的連續梁的抗彎強度，極限狀態法的安全儲備較容許應力法富余量稍大，采用容許應力法設計較為保守。

(2)對于連續梁的正截面抗裂性，極限狀態法的安全儲備較容許應力法富余量大，采用容許應力法設計較為保守，但對于關鍵截面，極限狀態法更為控制。

(3)對于連續梁的斜截面抗裂性，由于容許應力法計算中采用了1.2的安全系數，主拉應力值相較極限狀態法要高，且由于極限狀態法未考慮現澆施工的接縫對混凝土抗拉性能的降低，采用容許應力法設計時更為控制。

(4)總體上看，《暫規》[2]極限狀態法的設計參數取值是合理適用的，與《現規》[4]容許應力法的設計水準相當。

(5)結合檢算結果來看，《暫規》[2]中有部分公式的設計參數和限值需要進行修正和完善。

《現規》[4]中，對于制造工藝不符合工廠制造條件的結構，主力及主+附作用下的各項強度安全系數均應增大10%，而《暫規》[2]中并未考慮預制構件和現澆構件的差異，使得現澆構件的安全儲備相對降低較多，建議《暫規》[2]區分預制構件和現澆構件的強度檢算容許值。

《暫規》[2]4.1.2條給出作用效應的基本組合設計值表達式

Qk1為主導的可變作用，而《暫規》[2]4.1.1條又規定了列車活載、列車豎向動力效應及離心力為不同的基本可變作用，當列車活載為Qk1時，列車豎向動力效應及離心力就計算在Qkj當中了，顯然這樣是偏于不保守的，故建議《暫規》[2]應說明當列車活載為主導可變作用時，Qk1還應包含列車豎向動力效應及離心力。同樣，《暫規》[2]4.1.3條給出作用效應頻遇組合的設計值表達式中應說明當列車活載為主導可變作用時，不考慮沖擊影響。

《暫規》[2]7.3.8條規定，“對于預應力混凝土連續梁，……在檢算破壞階段的截面強度時，可不計預加力產生的二次力的影響”。而超靜定結構在承載能力極限狀態塑性鉸尚未完全形成[5]，所以在該狀態時由預加力引起的次效應，應予以考慮。

[1] 中國鐵路總公司.鐵路橋涵典型結構極限狀態法試設計設計細則[S].天津：鐵道第三勘察設計院集團有限公司，2015.

[2] 中國鐵路總公司.Q/CR9300—2014 鐵路橋涵極限狀態法設計暫行規范[S].北京：中國鐵道出版社，2014.

[3] 中華人民共和國鐵道部.TB 10002.1—2005 鐵路橋涵設計基本規范[S].北京：中國鐵道出版社，2005.

[4] 中華人民共和國鐵道部.TB 10002.3—2005 鐵路橋涵鋼筋混凝土和預應力混凝土結構設計規范[S].北京：中國鐵道出版社，2005.

[5] 中華人民共和國交通部.JTG D62—2004 公路鋼筋混凝土及預應力混凝土橋涵設計規范[S].北京：人民交通出版社，2004.

[6] 周津斌.容許應力法與極限狀態法鐵路橋墩設計對比分析[J].鐵道標準設計，2016(9)：74-78.

[7] 朱志營，齊成龍.鐵路橋梁正常使用極限狀態可靠度校準研究[J].鐵道標準設計，2015(1)：80-83.

[8] 徐升橋，彭嵐平，侯建軍，等.鐵路橋梁承載能力可靠性分析[J].鐵道標準設計，2013(1)：45-52.

[9] 高策，薛吉崗.鐵路橋涵結構極限狀態法設計檢算分析[J].鐵道經濟研究，2013(5)：23-39.

[10] 中國鐵路總公司.Q/CR9007—2014 鐵路工程結構可靠性設計統一標準(試行)[S].北京：中國鐵道出版社，2014.

[11] 中華人民共和國交通部.JTG D60—2015 公路橋涵設計通用規范[S].北京：人民交通出版社，2015.

[12] 趙建昌.混凝土結構設計原理[M].北京：中國鐵道出版社，2004.

[13] 鐵道部第三勘測設計院.鐵路工程設計技術手冊·橋梁設計通用資料[M].北京：中國鐵道出版社，1994.

[14] 中華人民共和國鐵道部.鐵建設函[2005]285號 新建時速200 km客貨共線鐵路設計暫行規定[S].北京：中國鐵道出版社，2010.

[15] 鐵道部經濟規劃研究院.TZ203—2008 客貨共線鐵路橋涵工程施工技術指南[S].北京：中國鐵道出版社，2008.