基于改進(jìn)Mayr模型的弓網(wǎng)離線電弧仿真分析

喬 凱，劉文正，張 堅(jiān)，王天宇，龔兆豐

(1.北京交通大學(xué)電氣工程學(xué)院，北京 100044；2.中車青島四方機(jī)車車輛股份有限公司，青島 266111；3.北京地鐵運(yùn)營(yíng)有限公司供電分公司，北京 100044)

弓網(wǎng)離線電弧是弓網(wǎng)關(guān)系中的核心問題，嚴(yán)重影響了列車的運(yùn)行安全[1]。因此，有必要對(duì)弓網(wǎng)離線電弧的特性進(jìn)行深入的研究。

電弧模型作為研究電弧的重要手段之一，電弧的模型可分為兩種：一種為物理數(shù)學(xué)模型，它以電弧存在的整個(gè)過程中出現(xiàn)的物理現(xiàn)象為基礎(chǔ)進(jìn)行深入研究，雖然可以從電弧內(nèi)部的物理過程研究電弧，但電弧模型的建立依賴于大量假設(shè)，并且求解過程比較復(fù)雜；而另外一種為黑盒模型，只研究電弧的外部特性，即電弧電壓和電弧電流關(guān)系的宏觀研究。本文主要研究弓網(wǎng)離線電弧電壓和電流的特性，因此，采用黑盒模型建立弓網(wǎng)離線電弧的動(dòng)態(tài)模型。

從電弧外部物理過程著手研究最早的是Cassie電弧模型[2]和Mayr電弧模型[3]。文獻(xiàn)[4]對(duì)低壓交流電線故障電弧模型進(jìn)行了研究。文獻(xiàn)[5]基于Mayr電弧模型和Cassie電弧模型提出了一種用于大功率電弧加熱器的等離子電弧模型。文獻(xiàn)[6]基于Mayr和Cassie電弧微分方程建立了輸電線路單端測(cè)距用的高阻接地故障電弧模型。文獻(xiàn)[7]對(duì)弓網(wǎng)離線電弧產(chǎn)生的離線過電壓進(jìn)行了仿真分析。文獻(xiàn)[8]基于Mayr電弧模型模擬仿真氣吹滅弧，得到了如下結(jié)果：高速氣體對(duì)間隙電弧的快速熄滅有明顯效果。文獻(xiàn)[9]基于Mayr電弧模型對(duì)氣流與電弧熄弧特性進(jìn)行了深入討論。文獻(xiàn)[10]將Mayr和Cassie電弧方程聯(lián)合起來建立了水中電弧的數(shù)學(xué)模型。文獻(xiàn)[11]基于Mayr方程建立參數(shù)化的PSCAD電弧電阻模型。

本文分析了高速氣流和氣象環(huán)境因素(例如：氣壓、空氣濕度、溫度等)對(duì)弓網(wǎng)離線電弧特性的影響。由文獻(xiàn)[12]知，氣象環(huán)境因素對(duì)擊穿電弧的放電過程影響較大，而對(duì)拉弧的放電過程影響較小，而弓網(wǎng)離線電弧屬于拉弧，所以氣象環(huán)境因素對(duì)弓網(wǎng)離線電弧的特性影響較小；高速氣流對(duì)弓網(wǎng)離線電弧特性的影響較大。本文主要研究了高速氣流對(duì)弓網(wǎng)離線電弧耗散功率的影響，并基于此對(duì)Mayr電弧模型進(jìn)行了優(yōu)化改進(jìn)，建立了弓網(wǎng)離線電弧動(dòng)態(tài)模型。并利用建立的弓網(wǎng)離線電弧動(dòng)態(tài)模型研究了列車運(yùn)行速度和離線間距對(duì)弓網(wǎng)離線電弧燃弧尖峰電壓和熄弧尖峰電壓的影響。

1 弓網(wǎng)離線電弧動(dòng)態(tài)模型的建立

1.1 Mayr電弧模型

由文獻(xiàn)[3]知，Mayr認(rèn)為電弧的形狀是圓柱形的，其直徑是不變的；從電弧弧柱散出的能量是不發(fā)生變化的，能量的耗散是依靠傳導(dǎo)作用和輻射作用。

Mayr假定：

(1)電弧為一直徑不變的圓柱體，在圓柱體中心的溫度最高，圓柱體外圍的溫度逐漸降低；

(2)電弧的能量耗散主要因?yàn)榕c周圍氣體的熱傳導(dǎo)及熱輻射作用，不考慮熱對(duì)流以及電極散熱的耗散，其耗散功率為一常數(shù)值；

(3)弧柱中氣體的物理性質(zhì)保持不變，不考慮溫度變化的影響。其帶電粒子的熱游離情況由沙哈方程確定。

Mayr電弧模型的方程式為

(1)

式中，g、u、i、θ和Ploss分別為電弧電導(dǎo)、電弧電壓、電弧電流、電弧時(shí)間常數(shù)和電弧耗散功率。

1.2 改進(jìn)Mayr電弧模型

實(shí)際的弓網(wǎng)離線電弧都會(huì)受到由列車運(yùn)行速度引起的高速氣流的影響，因此有必要研究高速氣流對(duì)弓網(wǎng)離線電弧特性的影響。但在實(shí)驗(yàn)過程中模擬高速氣流比較困難，所以仿真手段就顯得異常重要。國(guó)內(nèi)外學(xué)者對(duì)Mayr電弧模型進(jìn)行不同的修正與完善，主要是通過確定電弧耗散功率Ploss和電弧時(shí)間常數(shù)θ受哪些影響因素影響及它們之間的函數(shù)關(guān)系。本文基于能量平衡理論和橫向吹弧理論，對(duì)弓網(wǎng)離線電弧弧柱的能量過程進(jìn)行了數(shù)學(xué)分析，研究了高速氣流對(duì)弓網(wǎng)離線電弧耗散功率的影響，確立了電弧耗散功率Ploss和列車運(yùn)行速度v、電流I和離線間距l(xiāng)之間的函數(shù)關(guān)系。由文獻(xiàn)[12]知，在空氣中自由燃熾的電弧或者是受縱向或橫向氣流作用的電弧，對(duì)流散熱PK占到總能量耗散的80%以上。因此對(duì)流散熱在弓網(wǎng)離線電弧中起著重要作用，占弧柱散出功率的極大部分。

首先，電弧能量的耗散功率包含3個(gè)部分，傳導(dǎo)功率PT、對(duì)流功率PK、輻射功率PS，他們之間的關(guān)系如式(2)所示

Ploss=PT+PK+PS

(2)

由文獻(xiàn)[12]知，輻射功率一般占總功率的10%左右，受縱向或橫向氣流吹的電弧基本上是對(duì)流散熱，完全可以忽略傳導(dǎo)散熱，所以

Ploss=PK+PS=PK+10%Ploss

(3)

按吹弧方向的不同，吹弧可分為以下兩種：吹弧的氣流沿電弧方向的吹拂稱為縱吹，如圖1(a)所示。橫吹時(shí)氣流的方向與電弧的軸線方向垂直，如圖1(b)所示。在弓網(wǎng)離線電弧中，弧柱的方向是垂直于列車運(yùn)動(dòng)方向，如圖1(c)所示。氣流場(chǎng)橫向吹弧對(duì)弓網(wǎng)離線電弧的作用要遠(yuǎn)遠(yuǎn)大于縱向吹弧。所以本文只考慮橫向吹弧對(duì)弓網(wǎng)離線電弧特性的影響。

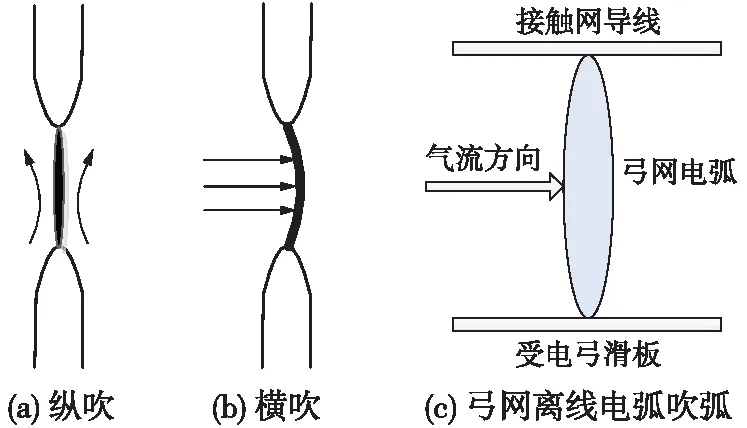
圖1 吹弧示意

由文獻(xiàn)[12]知，當(dāng)列車運(yùn)行速度為v時(shí)，電弧的直徑為d，空氣從溫度T0被加熱到電弧的平均溫度Tc，需要的單位長(zhǎng)度的熱量

(4)

式中，c為氣體的熱容系數(shù)，對(duì)于空氣，在一個(gè)大氣壓下，c可簡(jiǎn)單的表示為

(5)

將式(5)代入式(4)中，可得

(6)

(7)

在橫向吹弧的作用下，電弧的體積被壓縮，直徑減小，電流密度增大，電弧直徑是電弧電流和電弧運(yùn)動(dòng)速度的函數(shù)[13]

(8)

把式(8)帶入式(7)中得長(zhǎng)度為l(cm)的弓網(wǎng)離線電弧對(duì)流散熱的功率

(9)

將式(9)代入式(3)，得到電弧耗散功率的計(jì)算公式

(10)

其次，電弧時(shí)間常數(shù)的計(jì)算公式為[14]

(11)

其中，α為比例系數(shù)2.85×10-5；I為電弧電流,A；l為電弧長(zhǎng)度，cm，以弓網(wǎng)離線間距近似代替；θ的單位為s。

2 弓網(wǎng)離線電弧動(dòng)態(tài)模型的搭建

首先，根據(jù)公式(1)在Simulink中搭建的電弧仿真電路如圖2所示。

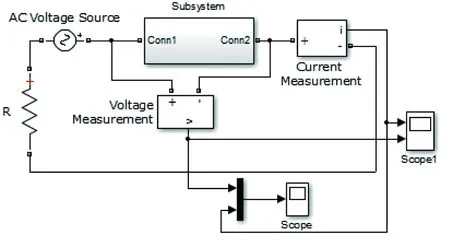
圖2 電弧模型外部電路

此電路由交流電壓源，電阻，電弧模塊，電弧電壓和電流測(cè)量模塊和示波器模塊組成。Subsystem模塊即為電弧模塊，它是一個(gè)可自由編輯的封裝子模塊，其內(nèi)部結(jié)構(gòu)如圖3所示。

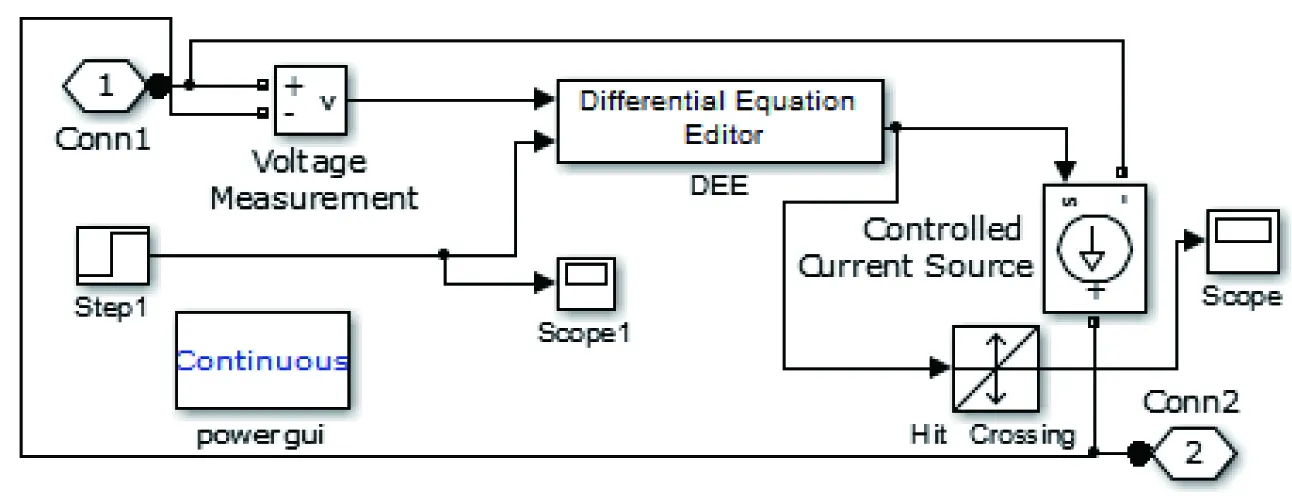
圖3 改進(jìn)的Mayr模型

該電弧子模塊主要由DEE模塊，階躍信號(hào)模塊和受控電流源模塊組成。DEE模塊是對(duì)電弧模型公式的微分實(shí)現(xiàn)；階躍信號(hào)模塊控制電弧產(chǎn)生的時(shí)刻；受控電流源接受DEE模塊的輸出信號(hào)，從而產(chǎn)生相應(yīng)的電弧電流值。

其中，DEE模塊是實(shí)現(xiàn)電弧模型的最重要環(huán)節(jié)。其實(shí)現(xiàn)原理是將式(1)進(jìn)行變化得到，如式(12)所示。

(12)

式中，x(1)為微分方程狀態(tài)變量，即電弧電導(dǎo)的自然對(duì)數(shù)lg(g)；x(0)為電弧電導(dǎo)的初始值；u(1)為電弧電壓，也是DEE的第一個(gè)輸入量；u(2)為弓網(wǎng)離線的狀態(tài)，弓網(wǎng)離線前u(2)=0，弓網(wǎng)離線后u(2)=1，這也是DEE的第二個(gè)輸入量；y為電弧電流，也是DEE的輸出量；θ為電弧時(shí)間常數(shù)；P為電弧散熱功率。

3 弓網(wǎng)離線電弧模型的驗(yàn)證與仿真結(jié)果分析

3.1 弓網(wǎng)離線電弧模型的驗(yàn)證

本文采用仿真與實(shí)驗(yàn)相結(jié)合的方法對(duì)搭建的弓網(wǎng)離線電弧模型進(jìn)行驗(yàn)證。如果弓網(wǎng)離線電弧模型仿真得到的波形和實(shí)驗(yàn)得到的波形在定性分析上一致，則可以說明搭建的弓網(wǎng)離線電弧模型及其參數(shù)的設(shè)置合理，結(jié)果可信。

在前期的研究中，根據(jù)弓網(wǎng)離線電弧產(chǎn)生機(jī)理，課題組研制了一套弓網(wǎng)離線電弧實(shí)驗(yàn)系統(tǒng)。文獻(xiàn)[17]介紹了弓網(wǎng)離線電弧實(shí)驗(yàn)系統(tǒng)及電弧電壓、電弧電流和電弧光強(qiáng)等實(shí)驗(yàn)波形，在仿真條件和實(shí)驗(yàn)條件完全相同的情況下，弓網(wǎng)離線電弧電壓仿真波形和弓網(wǎng)離線電弧電壓實(shí)驗(yàn)波形如圖4所示。

圖4 仿真與實(shí)驗(yàn)電弧電壓波形對(duì)比

由圖4可以看出，弓網(wǎng)離線電弧電壓仿真波形與實(shí)驗(yàn)波形在整體趨勢(shì)上較一致。即均有1個(gè)35 V左右的燃弧尖峰電壓與1個(gè)15 V左右的熄弧尖峰電壓，且在非尖峰階段電弧電壓保持穩(wěn)定在10 V左右。值得注意的是，由于弧柱氣體具有熱慣性的作用，相同電流時(shí)熄弧階段的電弧電阻要比起弧階段小，所以熄弧尖峰電壓小于燃弧尖峰電壓。

弓網(wǎng)離線電弧的伏安特性曲線如圖5所示，對(duì)比圖5(a)和圖5(b)可知，由仿真得到的曲線圖和實(shí)驗(yàn)得到的曲線圖具有相同的變化規(guī)律。由圖5可知，弓網(wǎng)離線電弧的伏安特性由2條線曲線組成，一條曲線是電流增加時(shí)的特性，另一條屬于電流減小時(shí)的特性。后一條曲線低于前一條，這是由于電極和弧柱氣體的熱慣性所致。值得注意的是，實(shí)測(cè)的弓網(wǎng)離線電弧伏安特性曲線并不關(guān)于原點(diǎn)對(duì)稱，其主要原因是弓網(wǎng)離線電弧2個(gè)極的形狀和電極材料均不同。

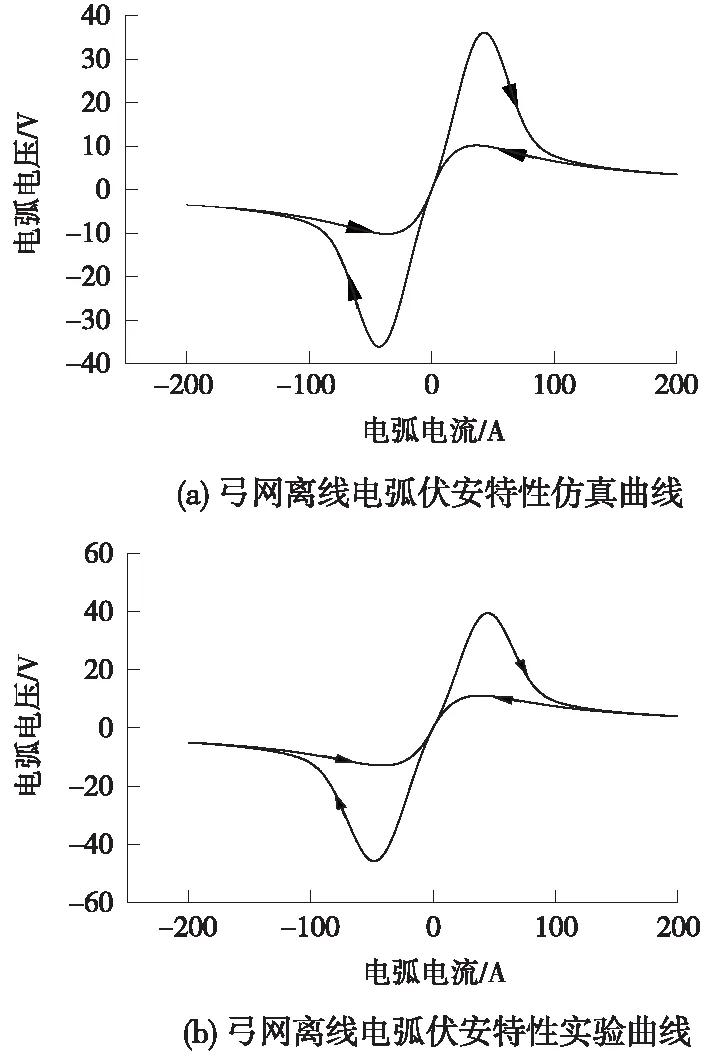
圖5 弓網(wǎng)離線電弧伏安特性

綜上所述，本文改進(jìn)的Mayr電弧模型及其設(shè)置的參數(shù)適合描述弓網(wǎng)離線電弧現(xiàn)象。

3.2 仿真結(jié)果分析

由式(10)分析可知，電弧耗散功率隨著列車運(yùn)行速度提高和離線間距的增大而增大，所以本文接下來研究列車運(yùn)行速度和離線間距對(duì)弓網(wǎng)離線電弧電壓特性的影響。

首先設(shè)置列車的運(yùn)行速度分別為100、200、300 km/h，電流有效值I=300 A，離線間距為0.3 cm。根據(jù)公式(10)計(jì)算電弧耗散功率如表1所示，由式(11)計(jì)算電弧時(shí)間常數(shù)θ=2.85×10-2s。不同運(yùn)行速度條件下電弧電壓的仿真波形如圖6(a)所示。設(shè)置列車的運(yùn)行速度為300 km/h，電流有效值I=300 A，離線間距分別為0.1、0.3、0.5 cm。根據(jù)式(10)和式(11)計(jì)算得到電弧耗散功率和電弧時(shí)間常數(shù)如表2所示。不同離線間距條件下電弧電壓的仿真波形如圖6(b)所示。

表1 運(yùn)行速度對(duì)電弧耗散功率的影響

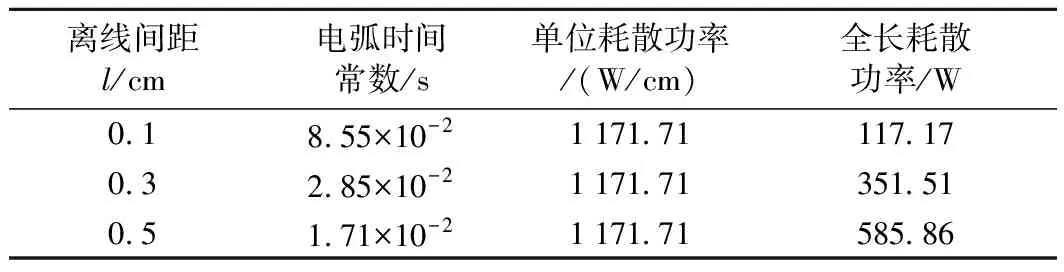
表2 離線間距對(duì)電弧耗散功率和電弧時(shí)間常數(shù)的影響

圖6 不同運(yùn)行速度和離線間距下的電弧電壓仿真波形

由圖6可以看出，隨著運(yùn)行速度的提高和離線間距的增大，電弧電壓的變化規(guī)律相同，即電弧電壓波形均呈馬鞍形，有一個(gè)較大的燃弧尖峰電壓和一個(gè)較小的熄弧尖峰電壓。隨著列車運(yùn)行速度的提高和離線間距的增大，電弧電壓的燃弧尖峰電壓和熄弧尖峰電壓均增大。這是由于隨著列車運(yùn)行速度的提高和離線間距的增大，電弧的耗散功率增加。根據(jù)弧隙能量平衡理論[14]可知，隨著能量散出的增加，電弧溫度下降，弧隙電阻增加，電弧重燃會(huì)更加困難，相應(yīng)的電弧燃弧尖峰電壓會(huì)增大。隨著耗散功率的增加，電極和弧柱氣體的熱慣性減小，相應(yīng)的電弧熄弧尖峰電壓增大。

4 結(jié)論

(1)基于能量平衡理論和橫向吹弧理論，對(duì)弓網(wǎng)離線電弧弧柱的能量過程進(jìn)行了分析，建立了電弧耗散功率Ploss和車速v、電流I和離線間距l(xiāng)之間的函數(shù)關(guān)系。并基于此對(duì)Mayr電弧模型進(jìn)行了改進(jìn)，確立了弓網(wǎng)離線電弧的動(dòng)態(tài)模型。

(2)通過對(duì)比分析弓網(wǎng)離線電弧仿真波形與實(shí)驗(yàn)波形可知，電弧的燃弧尖峰電壓為35 V左右，熄弧尖峰電壓為15 V左右；由仿真得到的伏安特性曲線和實(shí)驗(yàn)得到的伏安特性曲線具有相同的變化規(guī)律；從而驗(yàn)證了改進(jìn)的Mayr電弧模型適合分析弓網(wǎng)離線電弧現(xiàn)象。

(3)隨著列車運(yùn)行速度的提高和離線間距的增大，氣流對(duì)電弧的吹弧作用更加顯著，電弧耗散功率增加，燃弧尖峰電壓和熄弧尖峰電壓均增大。

[1] 王萬崗.高速鐵路弓網(wǎng)電弧動(dòng)態(tài)特性研究[D].成都：西南交通大學(xué)，2013：2-3.

[2] 丁濤.電氣化鐵路受電弓/接觸線摩擦磨損性能及電特性研究[D].成都：西南交通大學(xué)，2011：30-31.

[3] 蔣幸昌.升降弓過程中弓網(wǎng)電弧研究[D].成都：西南交通大學(xué)，2011：1-2.

[4] Cassie A M. The orienovelle des arcs derupture etdela ririgidite des Circuit[C]∥CIGRE. Ohio， US:1939.

[5] Mayr O. Contribution to the theory of static and dynamic arcs[J]. Arch， Elec， 1943，37(1):589-608.

[6] 姜斌峰，王莉.低壓交流電線故障電弧模型研究[J].電力系統(tǒng)及其自動(dòng)化學(xué)報(bào)，2009，21(4):20-24.

[7] 戴雋文，郝瑞祥，游小杰.一種用于大功率電弧加熱器的等離子電弧模型[J].電工技術(shù)學(xué)報(bào)，2011，26(1):129-134.

[8] 孫月琴，倪江，王賓，等.應(yīng)用于輸電線路單端測(cè)距的高阻接地故障電弧模型分析[J].電力系統(tǒng)自動(dòng)化，2016，40(22):86-92.

[9] 范福強(qiáng).基于改進(jìn)Habedank電弧模型的弓網(wǎng)離線過電壓研究[D].成都：西南交通大學(xué)，2014：5-6.

[10] 譚社平，覃毅藩，莫小向.新型滅弧防雷間隙的研究與應(yīng)用分析[J].高壓電器，2012，48(6):89-93.

[11] Midya S， Bormann D， Schutte T， et al. Pantograph Arcing in Electrified Railways—Mechanism and Influence of Various Parameters—Part I: With DC Traction Power Supply[J]. IEEE Transactions on Power Delivery， 2009，24(4):1931-1939.

[12] Midya S， Bormann D， Schutte T， et al. Pantograph Arcing in Electrified Railways—Mechanism and Influence of Various Parameters—Part II: With AC Traction Power Supply[J]. IEEE Transactions on Power Delivery， 2009，24(4):1940-1950.

[13] Yu-jen Liu， Gary W. Chang， Huang M Huang. Mayr’s equation-based model for Pantograph Arc of high-speed railway traction system[J]. Power Delivery IEEE Transactions on， 2010，25(3):2025-2027.

[14] 王其平.電器電弧理論[M].北京：機(jī)械工業(yè)出版社，1991：101-143.

[15] 龍夢(mèng)妮.高速氣流作用的動(dòng)態(tài)電弧模型及實(shí)際線路雷擊特性分析[D].南寧：廣西大學(xué)，2012：12-13.

[16] 張節(jié)容.高壓電器原理和應(yīng)用[M].北京：清華大學(xué)出版社，1989：106-136.

[17] 劉文正，王溢斐，王天宇，等.離線時(shí)刻對(duì)弓網(wǎng)電弧特性的影響[J].高電壓技術(shù)，2016，42(11)：3524-3532.