以深化高職數(shù)學改革提高課堂教學效率

李海英 毛亞娟

（唐山職業(yè)技術(shù)學院基礎(chǔ)部，河北 唐山 063004）

高職數(shù)學課程要以能力培養(yǎng)為重點，根據(jù)不同專業(yè)不同的特點，以為專業(yè)服務(wù)這條主線貫穿整個課程的理論與實踐教學。在“理論夠用，突出工具性，服務(wù)專業(yè)，提高能力”的教改理念指導(dǎo)下有效改進高等數(shù)學的教學，使高等數(shù)學在教學內(nèi)容、課程體系等方面有新的突破；在教學方式和方法、教學過程和手段上反映時代的水平；內(nèi)容體系既要考慮數(shù)學知識的前后銜接又考慮專業(yè)要求，教學設(shè)計立足于學生的親身經(jīng)歷和動手實驗，面向每一名學生的個性發(fā)展，通過靈活開放的教學方法與手段，使不同水平、不同需求的學生都能有所收獲。

一、根據(jù)學生的基礎(chǔ)和專業(yè)需要，探索先進的教學模式、轉(zhuǎn)變教學理念

通過對我院近幾年學生的高考數(shù)學的成績進行調(diào)查，發(fā)現(xiàn)我院大部分學生的數(shù)學成績不高，學生基礎(chǔ)較差，初等數(shù)學知識掌握得不扎實，不喜歡數(shù)學，這就給高等數(shù)學的學習帶來一定的困難。由于不同專業(yè)對高等數(shù)學知識的需求有所差異，針對這種情況，教師一定要從各專業(yè)對數(shù)學知識的具體需求出發(fā)，有的放矢、針對不同專業(yè)制定合理的教學方案，教學內(nèi)容要為專業(yè)服務(wù)，遵從循序漸進的原則。課程以能力培養(yǎng)為重點，根據(jù)不同專業(yè)的特點，使為專業(yè)服務(wù)這條主線貫穿整個課程的理論與實踐教學。

通過與機電工程系、農(nóng)林工程系、信息工程系、財經(jīng)系開展課程建設(shè)研討及專業(yè)認知的研討活動，對不同專業(yè)對數(shù)學課的要求與機電工程系的部分專業(yè)教師探討了《高等數(shù)學》課程與專業(yè)的接口的模塊化教學模式，并達成了共識。動車，機電一體化、生產(chǎn)過程自動化、汽車修理以及汽車營銷等專業(yè)對高等數(shù)學的需求不盡相同，兩個汽車專業(yè)64個學時基本就可以，汽車檢測與維修專業(yè)對函數(shù)的要求較高，學生要想進一步的學習，數(shù)學知識是必要的，建議極限、導(dǎo)數(shù)和微積分都要學習，一般到二重積分就可以。模塊化的教學方式符合大多數(shù)數(shù)學教師的想法和學生的需求，既能滿足數(shù)學基礎(chǔ)知識的需要又能培養(yǎng)學生素質(zhì)、提高學生的能力，促進基礎(chǔ)學科與專業(yè)的結(jié)合，自動化專業(yè)對數(shù)學內(nèi)容要求較多，學生能學習到離散數(shù)學、線性代數(shù)、復(fù)變函數(shù)的一些內(nèi)容。結(jié)合高等數(shù)學課程建設(shè)的現(xiàn)狀，達成了預(yù)開設(shè)選修課程的想法，一方面可以學習數(shù)學軟件，另一方面加強了應(yīng)用性的訓練，對學生參加數(shù)學建模競賽起到積極的促進作用，達到提高能力的目的。

二、堅持理論聯(lián)系實際，把數(shù)學建模思想融入課堂教學

在課堂教學中，加強實踐性教學環(huán)節(jié)與應(yīng)用性環(huán)節(jié)，將數(shù)學實驗和數(shù)學建模的思想精神融入高等數(shù)學課程教學之中，提升學生學習高等數(shù)學的意識,進而培養(yǎng)學生利用數(shù)學思想去解決實際問題的能力。

數(shù)學建模有一個非常重要的思想——分析問題和解決問題。教學過程中把數(shù)學的定義、定理都當作一個數(shù)學模型去講，講數(shù)學的思想、數(shù)學的方法和數(shù)學的應(yīng)用，同時將科研的思想、方法與理論都盡可能地融入到課堂中，真正實現(xiàn)了教學、科研與創(chuàng)新人才培養(yǎng)的一體化。,

例如：我們在求變速直線運動的瞬時速度時，我們就把數(shù)學建模思想貫穿到學生的課堂學習過程之中。

第一步：問題條件假設(shè)

假設(shè)：t為時間，△t為時間的改變量，t+△t為終了時間，s為位移，△s為位移的改變量，v為物體在 時刻的速度，a為加速度，g為自由落體物體的加速度，且g=9.8 。

第二步：問題的提出

設(shè)一物體做變速直線運動，物體的運動位移s與時間t的關(guān)系為s=s(t)（也叫運動方程），求物體在任意時刻的速度.

第三步：解決問題，建立模型

計算物體在任意時刻t時的速度問題，就是計算物體在 時刻的瞬時速度問題，也是計算運動物體函數(shù)在t時刻的極限問題，其實質(zhì)就是在求物體的運動函數(shù)在t時刻的導(dǎo)數(shù).我們把它歸納為變速直線運動的瞬時速度導(dǎo)數(shù)模型.我們把引起速度變化的變量變化情況用下圖1表示出來，如下.

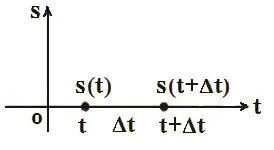
圖1

則t時刻的瞬時速度的導(dǎo)數(shù)模型為：

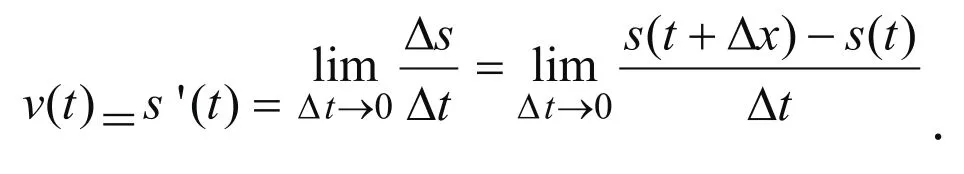
從而得出結(jié)論：變速直線運動的速度是某一時刻的位移關(guān)于時間的變化率，

具體問題： 物體做勻變速直線運動，初速度為10米/秒，加速度米/秒，求物體的運動方程及第30秒的瞬時速度。

解： 由題意得：則由得

得物體的運動方程為s=10t+t2

由瞬時速度的導(dǎo)數(shù)模型得物體的瞬時速度為

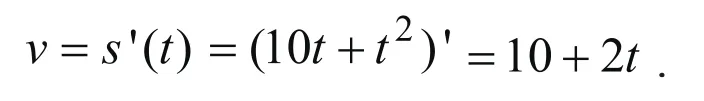
所以第30秒時的瞬時速度為

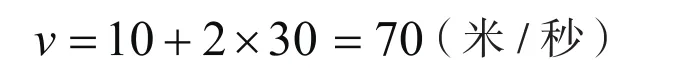
因此，數(shù)學建模思想融入課堂教學之中，可以是學生把學到的數(shù)學知識應(yīng)用到解決實際問題中來，實現(xiàn)理論與實踐一體化。

三、合理利用現(xiàn)代化教學手段，提高課堂教學效率

現(xiàn)代化教學手段能有效地增大每一堂課的教學內(nèi)容還能減輕教師板書的工作量，使教師能把更多的時間和精力投放在引導(dǎo)學生探究重點、難點問題上，提高講解效率。由于使用多媒體課件，使抽象的問題直觀化，容易激發(fā)學生的學習興趣，有利于啟發(fā)學生的形象思維，有利于提高學生的學習主動性，既調(diào)動了學生學習的積極性，又培養(yǎng)了學生分析問題的方法。達到了化難為易的目的，從而提高教學效率。

依托網(wǎng)絡(luò)，利用高等數(shù)學省級精品課程，微課程，鼓勵學生課前在網(wǎng)上學習，隨時與教師進行在線交流，突出了學生的主體地位，達到了預(yù)期的學習效果，實現(xiàn)課內(nèi)外教學一體化。通過建立網(wǎng)上交流平臺，在輔助教學課件、網(wǎng)絡(luò)課程、在線答疑等現(xiàn)代化教學手段的強有力支持，全面、合理地利用多媒體、因特網(wǎng)、校園網(wǎng)和教學資源平臺等現(xiàn)代化的教學手段進行教學，調(diào)動學生的參與性和能動性，達到較好的教學效果。

四、善于通過多渠道獲取反饋信息，優(yōu)化課堂教學過程

過程的可控程度，常取決于信息的交流暢通程度，特別是取決于反饋作用。所以教師要善于充分利用各種反饋方法，隨時收集從各個渠道來的反饋信息，才能針對信息進行有效地調(diào)控。教師應(yīng)充分利用各種反饋方法，及時收集多渠道的反饋信息。教師可以從學生的喜、怒、哀、樂等情緒表現(xiàn)中獲取學生的學習狀態(tài)；從答問、練習、檢測中了解學生課堂中對所學知識的掌握程度；從課上輔導(dǎo)、課下交流中把握學生的個性差異……這是教師可以直接獲取的第一手信息；另外，我們還可以通過學生對教師的評教測評和問卷調(diào)查，獲取第二手信息。對于這些信息教師要認真分析和反思，有針對性地對自己的課堂教學進行及時有效的改進。

總之，要通過高職數(shù)學課堂教學改革讓學生在數(shù)學學習中認識到學好數(shù)學對于本專業(yè)學習的重要性，從而用數(shù)學的眼光去解決本專業(yè)的實際問題。培養(yǎng)學生的基本數(shù)學能力、用數(shù)學知識解決專業(yè)問題的能力，使學生的學習能力得到最大的提高，適應(yīng)專業(yè)、崗位和社會對高技能人才的需求。

[1] 覃思義.徐全智.杜鴻飛.黃廷祝.數(shù)學建模思想融入大學數(shù)學基礎(chǔ)課的探索性思考及實踐[J].中國大學教學，2010(03)：36-39.

[2] 陸鐳.數(shù)學建模思想融入大學數(shù)學基礎(chǔ)課的探索與研究[J].科技展望，2016(03)：183-184.

[3] 杜健.丁士擁.董玉才.大學數(shù)學主干課程融入數(shù)學建模思想的研究與實踐[J].信息系統(tǒng)工程，2016(03)：148-149.