排列、組合、二項式定理的基本題型
■河北省唐山市海港高級中學 曹樹聰
■河北省唐山市海港高級中學 曹樹聰
一、計數原理
例1 如圖1,用6種不同的顏色給圖中的4個格子涂色,每個格子涂一種顏色,要求最多使用3種顏色且相鄰的兩個格子顏色不同,則不同的涂色方法共有____種(用數字作答)。
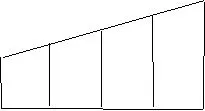
圖1
解析:采用間接法。根據乘法原理,對每一個格子依次涂色,共有6×5×5×5=750(種),再去掉使用4種顏色的涂色方法數A46=360(種),則所求的涂色方法數為750-360=390(種)。
二、排列問題
例2 (2017·天津卷)用數字1,2,3,4,5,6,7,8,9組成沒有重復數字,且至多有一個數字是偶數的四位數,這樣的四位數一共有____個。(用數字作答)
解析:滿足條件的四位數有兩種情況:一是沒有一個數字是偶數的四位數;二是正好有一個數字是偶數的四位數。故共有=1080(個)。
三、組合問題
例3 (2017·浙江卷)從6男2女共8名學生中選出隊長1人,副隊長1人,普通隊員2人組成4人服務隊,要求服務隊中至少有1名女生,共有____種不同的選法。(用數字作答)
解析:(方法一)完成這件事情分兩類:第一類,服務隊中只有1名女生,先從2名女生中選取1名女生,共有種方法,再從6名男生中選取3名男生,共有種方法,然后在這已選取的4名學生中選取1名隊長,1名副隊長,共有種方法,因此第一類共有=480(種)選法;第二類,服務隊中有2名女生,先從2名女生中選取2名女生,只有1種方法,再從6名男生中選取2名男生,共有種方法,然后在這已選取的4名學生中選取1名隊長,1名副隊長,共有種方法,因此第二類共有1×=180(種)選法。所以完成這件事情共有480+180=660(種)選法。
(方法二)考慮間接法:所有可能的情況為,其中不含有女生的情況有,所以=840-180=660(種)選法。
四、求二項式展開式的指定項或常數項

五、求二項式展開式的指定項的系數
例5 (2017全國卷Ⅲ)(x+y)(2xy)5的展開式中x3y3的系數為( )。
A.-80 B.-40 C.40 D.80
解析:(x+y)(2x-y)5=x(2x-y)5+y(2x-y)5,由(2x-y)5展開式·(2x)5-r(-y)r可得,r=3時,x(2x-y)5中x3y3的系數為×(-1)3=-40;r=2時,y(2x-y)5中x3y3的系數為×(-1)2=80。故x3y3的系數為80-40=40,應選C。
六、求二項式展開式中符合要求項的個數
例6的冪的指數是整數的項共有( )
A.3項 B.4項 C.5項 D.6項
解析,故6|(72-5r),即6|r。而r∈[0,24],所以r=0,6,12,18,24。共有5項,應選C。

