計數(shù)問題求解中的常見誤區(qū)

■河南省鄭州市七中 陳紅周

計數(shù)問題類型繁多、方法多變,同學們解題時極易出錯。但同學們求解時若能掌握最基本的原理和方法,按元素的性質(zhì)進行分類、按事件發(fā)生的過程分步,多留心易出錯的誤區(qū),積累常見的方法和模型,就能夠以不變應萬變,準確求解計數(shù)問題。

誤區(qū)一 分類計數(shù)時忽略分類的標準導致重復或遺漏

例1 某學校的特色班有40個人是音樂愛好者,有40個人是繪畫愛好者,其中30人是這兩種愛好兼而有之,現(xiàn)從中選出1人參加競技比賽,有多少種不同選法?

錯解:分兩類:第一類選音樂愛好者,有40種選法;第二類選繪畫愛好者,有40種選法。則不同選法共有40+40=80(種)。

剖析:分類計數(shù)原理要求同一種方法不能歸于不同的類,即分類要清。錯解原因是分類時沒有明確分類標準而導致錯誤。

正解:事件分三類:第一類,選只愛好音樂的人,有10種方法;第二類,選只愛好繪畫的人,有10種方法;第三類,選既是音樂愛好者又是繪畫愛好者,有30種方法。

所有不同選法共有:

10+10+30=50(種)。

例2 某文藝團體有10人,每人至少會唱歌或跳舞中的一種,其中7人會唱歌,5人會跳舞,從會唱歌與會跳舞的人中各選出1人,有多少種選法?

錯解:由題意知,10人中只會唱歌的有5人,只會跳舞的有3人,既會唱歌又會跳舞的有2人。從中選出會唱歌與會跳舞的各1人的選法分為三類:第一類,從只會唱歌的5人中選1人,從只會跳舞的3人中選1人,共有5×3=15(種)不同的選法;第二類從只會唱歌的5人中選1人,從既會唱歌又會跳舞的2人中選1人,共有5×2=10(種)不同的選法;第三類從只會跳舞的3人中選1人,從既會唱歌又會跳舞的2人中選1人,共有3×2=6(種)不同的選法。由分類計數(shù)原理知,不同選法共有15+10+6=31(種)。

剖析:分類計數(shù)原理中的分類,是對所有方法進行分類,此解法的分類有遺漏,主要是忽略分類的標準而出現(xiàn)計數(shù)遺漏,造成少算。

正解:將元素自然分組,從會唱歌又會跳舞的2人入手,確定分類標準,選出會唱歌與會跳舞的各1人的選法分四類:第一、二、三類,同上;第四類,將既會唱歌又會跳舞的2人全部選出只有1種選法。由分類計數(shù)原理知,不同選法共有15+10+6+1=32(種)。

誤區(qū)二 對事件的理解不清,導致對各步的種數(shù)不確定出錯

例3 在3000與8000之間有多少個無重復數(shù)字的奇數(shù)?

錯解:分三步完成,先從數(shù)字3、4、5、6、7中取1個排在首位有5種排法,再從1、3、5、7、9這5個奇數(shù)中選1個排在個位有5種排法,最后排中間的兩位,有8×7種排法。

所以共有5×5×8×7=1400(個)無重復的奇數(shù)。

剖析:由題意知3、5、7這3個數(shù)字既可以排在首位,也可以排在個位,因此,首位排3、5、7還是排4、6影響到第二步填個位的方法種數(shù),使第二步的排法種數(shù)不確定,并且會使3、5、7在首位和個位有重復的情況,造成計算錯誤。遇到此種情形,應分類求解。

正解:事件可分兩類:第一類,3、5、7為首位的奇數(shù),排這樣的四位奇數(shù)可分三步,先排首位,從3、5、7中取1個有3種排法,再排個位,從余下的4個奇數(shù)中取1個排個位,有4種排法,最后排中間兩位有8×7種排法,這一類奇數(shù)共有3×4×8×7=672(個)。第二類:4、6為首位的四位奇數(shù)也分三步,先排首位,從4、6中取1個數(shù)有2種排法,再排個位,從1、3、5、7、9這5個奇數(shù)中取1個排個位,有5種排法,最后排中間兩位有8×7種排法,這一類奇數(shù)共有2×5×8×7=560(個)。

由分類計數(shù)原理知,滿足要求的奇數(shù)共有672+560=1232(個)。

誤區(qū)三 分類與分步混淆或分類與分步不準確

例4 50件產(chǎn)品中有4件次品,從中任意抽出5件,則至少有3件次品的抽法有____種。

錯解1:分兩類情形:“有3件次品”時,可從4件次品中抽取3件,再從剩余產(chǎn)品中抽取2件,有種抽法;“有4件次品”時,可從4件次品中抽取4件,再從剩余產(chǎn)品中抽取1件,有種抽法。

故抽法共有()=48833(種)。

錯解2:先抽次品,至少有3件次品包含“3件次品”、“4件次品”兩種情形,共有+=5(種)抽法;再抽剩余產(chǎn)品,共有+=1081(種)抽法。

則有抽法5×1081=5405(種)。

剖析:分類與分步混淆不清,加法原理與乘法原理混淆,從而引起以上錯誤。

正解:此題可分為兩類:第一類,有3件次品2件正品,分步有(分為兩步,用乘法原理)種抽法;第二類,有4件次品1件正品,分步有種抽法。由加法原理知,不同的抽法共有=4186(種)。

例5 從100到999的三位數(shù)中,含有0的三位數(shù)有多少個?

錯解:將含有0的三位數(shù)分為兩類:個位數(shù)是0的三位數(shù),有9×10=90(個);十位數(shù)是0的三位數(shù),有9×10=90(個)。

故共有90+90=180(個)三位數(shù)滿足題意。

剖析:分類應注意“不重不漏”,上解法中重復計算了個位和十位都是0的情形。

正解:將含有0的三位數(shù)分為兩類:個位數(shù)是0的三位數(shù),有9×10=90(個),十位數(shù)是0的三位數(shù),有9×10=90(個),但個位數(shù)是0且十位數(shù)也是0的9個數(shù)重復了。故滿足題意的三位數(shù)共有90+90-9=171(個)。

誤區(qū)四 未考慮元素的順序而引起失誤

例6 有大小形狀相同的3個紅球和5個白球排成一排,共有____種不同的排法。

錯解:因為是8個小球的全排列,所以共有種方法。

剖析:錯解中沒有考慮3個紅球之間及5個白球之間是完全相同的,而同色球之間互換位置是同一種排法。

正解:8個小球排好后對應著8個位置,題中的排法相當于在8個位置中選出3個位置給紅球,剩余的位置給白球,由于這3個紅球完全相同,所以沒有順序,是組合問題,故共有=56(種)排法。

例7 從1,2,3,…,10中選出3個不同的數(shù),使這3個數(shù)構成等差數(shù)列,則這樣的數(shù)列共有多少個?

錯解:根據(jù)構成的等差數(shù)列,公差可分為為1、2、3、4四類。公差為1時,有8個;公差為2時,首先將數(shù)字分成1,3,5,7,9和2,4,6,8,10兩組,再得到滿足要求的數(shù)列共3+3=6(個);公差為3時,有1,4,7和4,7,10和3,6,9以及2,5,8,共4個;公差為4時,只有1,5,9和2,6,10兩個。由分類計數(shù)原理可知,共構成了8+6+4+2=20(個)不同的等差數(shù)列。

剖析:上述解答忽略了1,2,3與3,2,1它們是不同的數(shù)列,因而導致考慮問題不全面,從而出現(xiàn)漏解。這需要在解題過程中全方位、多角度審視問題。

正解:根據(jù)構成的等差數(shù)列的公差,分為公差為±1、±2、±3、±4四類。公差為±1時,有8×2=16(個);公差為±2時,滿足要求的數(shù)列共6×2=12(個);公差為±3時,有4×2=8(個);公差為±4時,只有2×2=4(個)。由分類計數(shù)原理可知,共構成了不同的等差數(shù)列有16+12+8+4=40(個)。

例8 有甲、乙、丙三項任務,甲需要2人承擔,乙、丙各需要1人承擔,現(xiàn)在從10人中選派4人承擔這三項任務,不同的選法有( )種。

A.1260 B.2025

C.2520 D.5040

錯解1:分三步完成:首先從10人中選出4人,有種方法;再從這4人中選出2人承擔任務甲,有種方法;剩下的2人去承擔任務乙、丙,有種方法。由乘法原理知,不同的選法共有=5040(種),選D。

錯解2:分三步完成,不同的選法共有=1260(種),選A。

剖析:錯解都混淆了承擔任務甲的2人與順序無關,剩下的2人去承擔任務乙、丙,這與順序有關。

正解1:先從10人中選2人承擔任務甲,再從余下8人中選1人承擔任務乙,最后從剩下的7人中選1人去承擔任務丙。則不同的選法有=2520(種),選C。

正解2:從10人中選出2人承擔任務甲,再從余下8人中選出2人承擔任務乙、丙,則不同的選法有=2520(種),選C。

誤區(qū)五 分配、分組概念不清而導致重復計數(shù)

例9 5本不同的書全部分給4個學生,每個學生至少1本,則不同的分法種數(shù)為( )。

A.480 B.240 C.120 D.96

錯解:先從5本書中取4本分給4個人,有種方法,剩下的1本書可以給任意1人有4種分法,共有4×=480(種)不同的分法,選A。

剖析:設5本書a、b、c、d、e分給4人甲、乙、丙、丁。按照上述分法可能出現(xiàn)ae,b,c,d和ea,b,c,d的情形。第一種是甲首先分得a,最后分得e的情形;第二種是甲首先分得e,最后分得a的情形。這兩種情況是完全相同的,故錯解中重復計數(shù)了。

正解:首先把5本書轉(zhuǎn)化成4堆書,然后分給4個人。第一步:從5本書中任意取出2本當成一本書,有C25種方法;第二步:再把4本書分給4個學生,有A44種方法。由乘法原理知,共有C25·A44=240(種)方法,故選B。

誤區(qū)六 忽視題設條件引起失誤

例10 兩人進行乒乓球比賽,先贏三局者獲勝,則所有可能出現(xiàn)的情形(各人輸贏局次的不同視為不同情形)共有( )。

A.10種 B.15種

C.20種 D.30種

錯解:分三類:比分3∶0有1種情況;比分3∶1,即前3局中有2局勝,第四局必勝,共有=3(種)情況;比分是3∶2,即前4局中有2局勝,第五局必勝,共有=6(種)情況。故共有1+3+6=10(種)情況獲勝,故選A。

剖析:以上解法顯然對“各人輸贏局次的不同視為不同情形”理解錯誤,造成僅考慮某一人獲勝的情形而造成漏解。事實上,兩人都有獲勝的可能。

正解:只需把以上結果乘以2即可,選C。

例11 方程ay=b2x2+c中的a,b,c∈{-3,-2,0,1,2,3},且a,b,c互不相同,在所有這些方程所表示的曲線中,不同的拋物線共有( )。

A.60條 B.62條C.71條 D.80條

錯解:顯然a≠0且b≠0,故a,b的選取方法有A25=20(種);c可從剩余的4個數(shù)中任取1個,有4種方法。由乘法原理知共有20×4=80(種)不同方法,故選D。

剖析:錯解中,由于x2的系數(shù)為b2,當b=-2或2和b=-3或3時,方程出現(xiàn)重復。

正解:顯然a≠0,b≠0,方程變形得y=

(1)當b=-3時,若a=-2,c可取0,1,2,3四種情況;同理,a=1,a=2,a=3時,分別有四種情況。

(2)當b=3時,若a=-2,c可取0,1,2,-3四種情況;同理,a=1,a=2,a=-3時,分別有四種情況。

以上兩種情況下有9種重復,故共有16+7=23(條)。

(3)同理當b=-2或b=2時,共有16+7=23(條)。

(4)當b=1時,a=-3,c可取-2,0,2,3四種情況;同理,a=-2,a=2,a=3時,分別有四種情況,共有16條。

共有23+23+16=62(條)。故選B。

誤區(qū)七 間接法求解不相鄰問題分類不完備

例12 現(xiàn)有8個人排成一排照相,其中有甲、乙、丙3人不能相鄰的排法有( )。

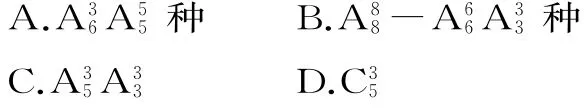
錯解:除甲、乙、丙三人以外的5人先排,有種排法。5人排好后產(chǎn)生6個空當,插入甲、乙、丙3人有種方法,這樣共有種排法,選A。

剖析:上面解法中將“甲、乙、丙3人不能相鄰”的含義誤解為“甲、乙、丙3人互不相鄰”的情形。事實上,“甲、乙、丙3人不能相鄰”是指甲、乙、丙3人不能同時相鄰,但允許其中有兩人相鄰。

正解:(排除法)在8個人全排列的方法數(shù)中減去甲、乙、丙全相鄰的方法數(shù),就得到甲、乙、丙3人不相鄰的方法數(shù),即種,故選B。

練一練:

1.高三年級的3個班到甲、乙、丙、丁4個工廠進行社會實踐,其中工廠甲必須有班級去,每班去何工廠可自由選擇,則不同的分配方案有( )。

A.16種 B.18種

C.37種 D.48種

答案:C

2.【2015年高考陜西卷理科第4題】二項式(x+1)n(n∈N*)的展開式中x2的系數(shù)為15,則n=( )。

A.4 B.5 C.6 D.7

答案:C

A.60 B.120 C.50 D.240

答案:B

提示:(x+1)10的展開式中x7的系數(shù)即可。

(x+1)10的二項展開式通項為Tr+1=,令10-r=7,r=3。x7的系數(shù)為=120,故答案為B。

4.【2015年高考安徽卷理科第11題】(用數(shù)字填寫答案)

提示:由題意知,二項式開式的通項為。令21-4r=5,得r=4,則x5的系數(shù)是=35。

5.【2015年高考新課標Ⅱ卷理科第15題】(a+x)(1+x)4的展開式中x的奇數(shù)次冪項的系數(shù)之和為32,則a=____。

提示:由已知得(1+x)4=1+4x+6x2+4x3+x4,故(a+x)(1+x)4的展開式中x的奇數(shù)次冪項分別為4ax,4ax3,x,6x3,x5,其系數(shù)之和為4a+4a+1+6+1=32,解得a=3。