為數學點贊
——名師例析數學文化（4）從楊輝三角到二項式定理

■北京市第十二中學高中部 高慧明

■北京市教育學院豐臺分院 張 琦

本刊特邀欄目專家簡介:

高慧明 首屆全國十佳班主任,全國著名數學特級教師,國家教育部課程改革“全國先進工作者”,全國著名高考數學命題與考試研究專家,國家教育部“國培計劃”全國中小學教師培訓、班主任培訓、校長培訓特邀主講專家,受邀在全國各地做有關高考科學備考、班級管理等多場專題報告。現任教于北京市第十二中學高中部。

高中數學教材人教A版《選修2—3》中用了較大篇幅介紹“楊輝三角”,并在探究與發現一欄中詳細介紹了“楊輝三角”中的一些秘密。究其原因,主要是“楊輝三角”蘊含了豐富的內容,由它可以直觀看出二項式定理的性質。同時“楊輝三角”又是我國古代數學的研究成果之一,它的發現顯示了我國古代勞動人民的卓越智慧和才能。

在介紹這部分內容之前,我們先來看看另外一部分大家不是很熟悉的內容——筆算開平方。整數,它與3×20的和,再乘以它本身,等于256。

為便于求得a,可用下面的豎式來進行計算:

根號上面的數3是平方根的十位數。將256試除以20×3,得4。由于4與20×3的和64,與4的積等于256,4就是所求的個位數a。豎式中的余數是0,表示開方正好開盡。于是得到1156=342,或 1156=34。

上述求平方根的方法,稱為筆算開平方法,用這個方法可以求出任何正數的算術平方根,它的計算步驟如下:

1.將被開方數的整數部分從個位起向左每隔兩位劃為一段,用撇號分開,分成幾段,表示所求平方根是幾位數。

2.根據左邊第一段里的數,求得平方根的最高位上的數(如上面豎式中的3)。

3.從第一段的數減去最高位上數的平方,在它們的差的右邊寫上第二段數組成第一個余數(如上面豎式中的256)。

4.把求得的最高位數乘以20去試除第一個余數,所得的最大整數作為試商(3×20除256,所得的最大整數是4,即試商是4)。

5.用商的最高位數的20倍加上這個試商再乘以試商。如果所得的積小于或等于余數,試商就是平方根的第二位數;如果所得的積大于余數,就把試商減小再試(如上面豎式中(20×3+4)×4=256,說明試商4就是平

一、筆算開平方

現在我們都知道,要想求某個數的平方根,最簡單的方法就是用計算器。但是在計算器出現之前,古人是怎么求一個數的平方根呢?本文做一簡單介紹。先一起來研究一下,怎樣求 1156,這里1156是四位數,所以它的算術平方根的整數部分是兩位數,且易觀察出其中的十位數是3。于是解決問題的關鍵在于:怎樣求出它的個位數a?為此,我們從a所滿足的關系式來進行分析。

根據兩數和的平方公式,可以得到:

1156=(30+a)2=302+2×30a+a2。

所以1156-302=2×30a+a2,即256=(3×20+a)a,這就是說,a是這樣一個正方根的第二位數)。

6.用同樣的方法,繼續求平方根的其他各位上的數。

按照上面步驟求 85264,可得到下面左邊的豎式。

于是得到

如遇開不盡的情況,可根據所要求的精確度求出它的近似值。例如求的近似值(精確到0.01),可列出上面右邊的豎式,并根據這個豎式得到。

二、楊輝三角

上述求平方根的方法是一個非常有效和高度機械化的算法,可適用于任意高次方。這種隨乘隨加、能反復迭代計算減根變換方程各項系數的方法,不論是在古代還是現代都有深遠的意義,而這也剛好是“開方做法本源”的本質。我們下面就對“開方做法本源”進行簡單的介紹。

楊輝是我國南宋時期的一位杰出的數學家。在他所著的《詳解九章算法》一書中,畫了一張表示二項式展開后的系數構成的三角圖形,稱為“開方做法本源”,現在簡稱為“楊輝三角”,它是世界的一大重要研究成果。根據楊輝的自注,這個三角形并不是楊輝發明的,因為他在《詳解九章算法》中表述其“出《釋鎖算書》,賈憲用此術”。所以,我們也可將其稱為“賈憲三角”。這一三角形的用途主要是開方,或者說解形如xn=A的高次方程。下面以求x3=2018的正根為例加以說明:

由于2018是四位數,可知其立方根在10～100之間,并由于2018大于103且小于203知其立方根的十位數字為1,故可設x=10+a,于是有(10+a)3=2018,按楊輝三角的第4行(1,3,3,1),可知103+3×102a+3×10a2+a3=2018,移項有300a+30a2+a3=1018。之后估計a的值,明顯能估算a大于2小于3,所以設a=2+b,重復上述過程,能夠達到想要的近似值。

為了能夠更好地說明“楊輝三角”的性質,我們暫時借用二項式系數進行說明。按圖1排成的三角形每一行的外側的數都是1,中間的數字等于其兩肩的數字的和。這一三角形最早發現于我國南宋數學家楊輝所著《詳解九章算法》一書(1261年),在我國通常稱為楊輝三角。

圖1

首先,讓我們來看看楊輝三角的某些性質。

1.項數:在楊輝三角的第n行的項數為(n+1)。

2.系數:在楊輝三角的第n行,各項的系數分別為:

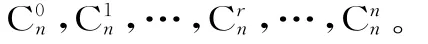
楊輝三角的第n行的系數和為C0n+

3.總項數:在楊輝三角形的n行及以上,

4.通項公式:

令Crn表示第n行第(r+1)個數,則這個

5.最大值:

在楊輝三角的第n行中:

當n=2m(m∈N*)時,二項式系數的最大值為,即中間的一項最大;

當n=2m+1(m∈N*)時,二項式系數的最大值為,即中間的兩項最大。

我們通過一個簡單的例子來體會一下“楊輝三角”的實際應用價值。

例1 如圖2所示,從甲地到乙地共有多少種不同的最近走法?

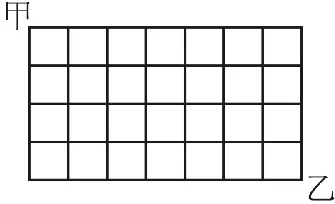
圖2

解析:為了討論方便,我們采取歸納猜想的方法進行求解。首先看最簡單的形式如圖3。可知從甲地到乙1地有2種走的方法。

之后我們可以將甲乙兩地之間的距離加大,到每個交叉點的走法剛好是如圖4所示標記的數字。

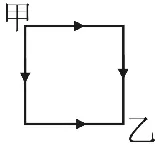
圖3

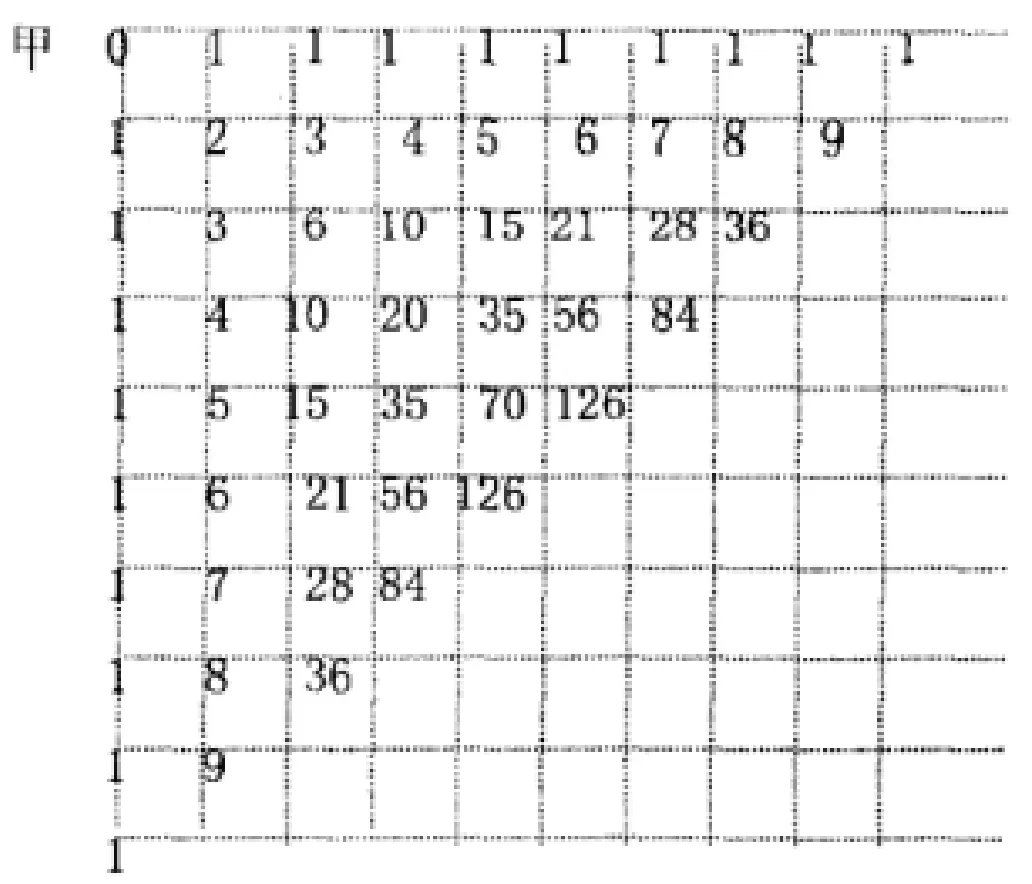
圖4

圖4所示從甲到每一個交叉點的走法與楊輝三角很相似,由此當我們遇到上面所示的路徑的問題時,我們可以根據楊輝三角來確定它到另一端的走法。其實這個圖形在西方數學史上也有記載,它是法國數學家帕斯卡發現的,被稱為“帕斯卡三角形”。

三、帕斯卡三角形

說到“帕斯卡三角形”,一定不能不提的就是概率論。

分賭注問題是概率論歷史上最著名的問題。1654年,職業賭徒德·梅累向法國數學家帕斯卡提出一個使他苦惱很久的分賭本問題:甲、乙兩賭徒賭技相同,各出賭注50法郎,每局中無平局。約定誰先贏滿5局,誰就獲得全部賭金。賭了半天,A贏了4局,B贏了3局,時間很晚了,他們都不想再賭下去了。那么,這個錢應該怎么分?是不是把錢分成7份,贏了4局的就拿4份,贏了3局的就拿3份呢?或者,因為最早說的是滿5局,而誰也沒達到,所以就一人分一半呢?

這個問題難住了帕斯卡,他苦苦思考了兩三年,才算有了點眉目。于是他寫信給自己的好友費馬,兩人討論結果,取得了一致的意見:既不是按4∶3分配,也不是按一人一半分配,而應該是按3∶1進行分配。

帕斯卡給費馬的信中寫道:由于第一人已得4分,另一人只有3分,他們擲下次時,若第一人贏了,他將獲得全部100法郎;若另一人贏了,他們的比分是4∶4,在這種情況下分賭注的話,每人將拿回自己所下的賭金,即50法郎。綜上,第一個人贏了,將獲得100法郎,如果他輸了,50法郎將屬于他。假設他不愿意繼續賭下去而要分賭金的話,第一個人應該說:我一定能得50法郎,即使我下一輪輸了,也應該把它們給我。至于另外的50法郎,也許我得到它們,也許你得到它們,機會是均等的。所以在分給我50法郎后,讓我們均分另外的50法郎吧。這樣,他將得到75法郎,而另外一個人只能得到25法郎。

如果是誰贏滿6局誰就獲得全部賭金,同樣甲贏了4局,乙贏了3局,如何分配賭資呢?費馬的解法是,如果繼續賭局,最多只要再賭4輪便可決出勝負,如果用“甲”表示甲方勝,用“乙”表示乙方勝,那么最后4輪的結果,不外乎以下16種排列:

甲甲甲甲 甲甲乙乙 甲乙乙乙

甲甲甲乙 甲乙甲乙 乙甲乙乙

甲甲乙甲 甲乙乙甲 乙乙甲乙

甲乙甲甲 乙乙甲甲 乙乙乙甲

乙甲甲甲 乙甲乙甲 乙乙乙乙

乙甲甲乙

甲方勝 乙方勝

在這16種排列中,當甲出現2次或2次以上時,甲方獲勝,這種情況共有11種;當乙出現3次或3次以上時,乙方勝出,這種情況共有5種。因此,賭金應當按11∶5的比例分配。

而帕斯卡解決這個問題則利用了他的“算術三角形”的數陣(見圖5,轉個觀察角度可以發現,其實就是一個楊輝三角,每條對角線上數就是二項展開式逐項的系數,帕斯卡還用組合數意義對其進行了解釋),歐洲人常稱之為“帕斯卡三角形”。

圖5

在一般情況下,如果甲需要再贏a局獲勝,乙需要再贏b局獲勝,那么就可以選擇“算術三角形”中第a+b條對角線,并求出這條對角線上前a個元素的和與后b個元素的和,賭注再按所得和之比來分配。由圖5可知,三角形第五行上的數恰好是甲出現次數的組合數,其中1是甲出現4次的組合數,4是甲出現3次的組合數,……因此賭金應按照11∶5的比例分配,這與費馬得到的結果是完全一致的。

后來,數學家雅可布·伯努利將其推廣到兩個水平不同,獲勝機會不均等的情形,而結果與二項式定理又有著結構上的驚人的相似:如果甲獲勝的概率為p,乙獲勝的概率為1-p,則甲在n局中能夠勝r局的概率為Crnpr(1-p)n-r。這就是教材中介紹的“二項分布”。

四、二項式定理

二項式定理,又稱牛頓二項式定理。牛頓于1664年提出之后,歷經幾個世紀的應用與發展,其經典性不言而喻。歷史上的二項式定理,和我們現在教科書中介紹的還是有些區別的,下面進行簡單介紹。

牛頓二項式用現在的式子及記號表示為:

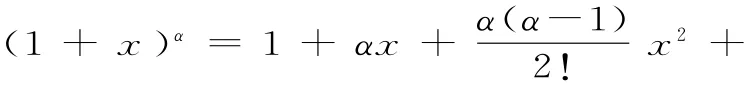
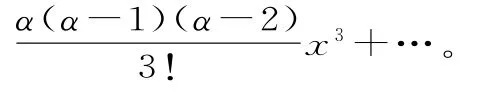
上式對于正整數α顯然成立,這也就是我們高中階段介紹的二項式定理。牛頓猜想對于任意的α∈R,上式都成立。萊布尼茨請牛頓說明是如何得到的,牛頓在信件中詳細說明了其發現過程。

牛頓注意到對n取偶數時,列出了不同次冪的系數:

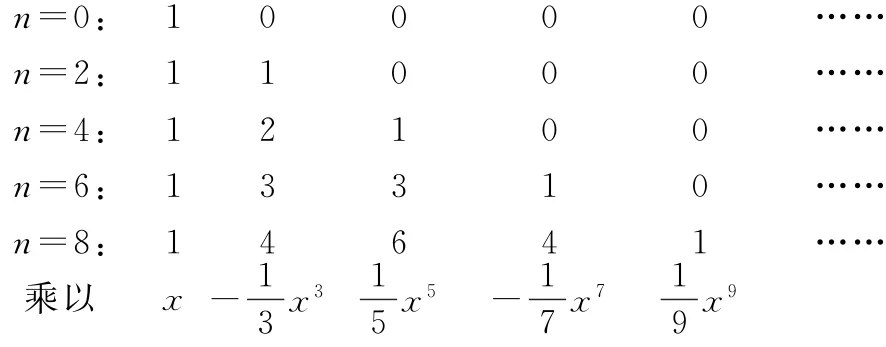
牛頓發現了其中的規律:將每一行中的第i項與第i-1項相加即可得到下一行中的第i項。

接下來,牛頓考慮n為奇數的情況。牛頓仔細研究了其中數字的形式,直到可以讀懂字里行間的意思。牛頓發現了其中規律:

上面“階梯”的第1列是:1;

第2列是:n;

……

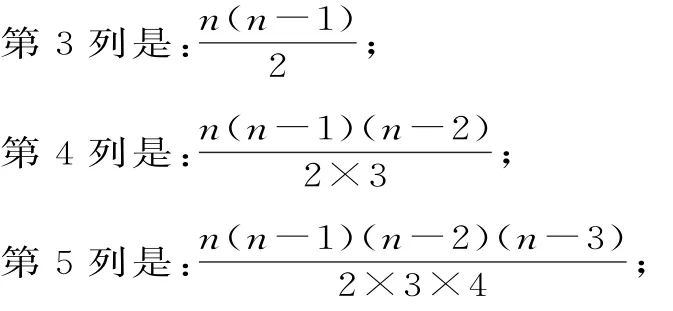
以此類推。

表1

按照上述方法,牛頓得到了:

對上式微分,有:

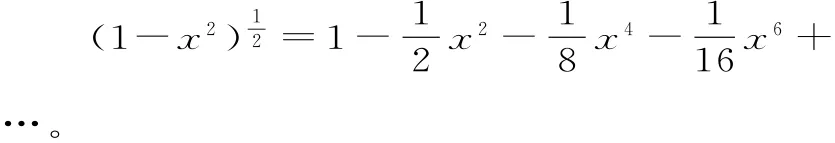
牛頓清楚地知道他是如何得到上述式子的,他還通過其他方法對所得結果進行驗證,發現都是正確的,從而,使他確信所得結果正確。由此,牛頓得到其著名的公式:

牛頓還運用這個“牛頓二項式定理”處理了許多有趣的級數,比如,他由此推出了反正弦函數的冪級數展開式及正弦函數的冪級數展開式。

當α為正整數時,就是我們高中階段介紹的二項式定理。下面我們通過幾個例題體會一下相關知識在試題中是怎么體現其作用的。

例2 (2004年上海春季高考卷)如圖6,在由二項式系數所構成的楊輝三角中,第____行中從左到右第14個與第15個數的比為2∶3。

圖6

解析:本題是關于“楊輝三角”的一道高考題。楊輝三角中蘊含著許多有趣的數量關系,與排列、組合和概率的關系非常密切。因此,理解和掌握楊輝三角的一些性質,對發現某些數學規律是很有幫助的。

由圖6我們能發現,第1行中的數是,;第2行中的數是;第3行中的數是;…;第n行中的數是。設第n行中從左到右第14個與第15個數的比為2∶3,則=2∶3,解得n=34。

例3 觀察下列數表,問此表最后一個數是什么,并說明理由。

解析:本題是一道以“楊輝三角”為背景的一道考題。通過觀察找出每一行數據間的相互聯系以及行與行間數據的相互聯系。然后對數據間的這種聯系用數學式子將它表達出來,使問題得解。因為第一行有100個數,以后每一行都比前一行少一個數,因此共有100行。

通過觀察可以得到:

第1行首尾兩項之和為101;

第2行首尾兩項之和為101×2;

第3行首尾兩項之和為101×22;

第4行首尾兩項之和為101×23;

……

第99行首尾兩項之和為101×298。

因為從第2行開始每一個數字是它肩上兩個數字之和,所以最后一個數字即第100行的數字是它肩上第99行首尾兩個數字之和,即為101×298。