計數原理拔高卷（A卷）

■北京師范大學萬寧附屬中學 劉金泉

編者的話:強化對核心考點的演練、注重對經典題型的歸納,是學好數學的秘訣,基于此,本刊編輯部特開設此欄目,希望同學們能認真練習。

一、選擇題

1.完成某項測試要過兩關,第一關有3種測試方案,第二關有5種測試方案,某人參加該項測試,不同的測試方案種數為( )。

A.3+5 B.3×5 C.35D.53

2.如圖1,從A城到B城有3條路;從B城到D城有4條路;從A城到C城有4條路,從C城到D城有5條路,則某旅客從A城到D城共有n條不同的路線,則n=( )。

A.16 B.24 C.32 D.64

3.甲、乙兩人從4門課程中各選修2門,則甲、乙所選的課程中恰有1門相同的選法有( )。

A.6種 B.12種

C.24種 D.30種

4.三張卡片的正反面分別寫有1和2,3和4,5和6,若將三張卡片并列,可得到不同的三位數(6不能作9用)的個數為( )。

A.8 B.6 C.14 D.48

5.有4位教師在同一年級的4個班中各教1個班的數學,在檢測時要求每位教師不能在本班監考,則不同的監考方法有( )。

A.8種 B.9種

C.10種 D.11種

6.將一個四面體A-BCD的六條棱上涂上紅、黃、白三種顏色,要求共端點的棱不能涂相同顏色,則不同的涂色方案有( )。

A.1種 B.3種 C.6種 D.9種

7.小明有4枚完全相同的硬幣,每個硬幣都分正反兩面,他想把4個硬幣擺成一摞,且滿足相鄰兩枚硬幣的正面不能相對,則不同的擺法有( )。

A.4種 B.5種 C.6種 D.9種

8.25人排成5×5方陣,從中選出3人,要求其中任意2人既不同行也不同列,則不同的選法有( )。

A.60種 B.100種

C.300種 D.600種

9.一個旅游景區的游覽線路如圖2所示,某人從點P處進,點Q處出,沿圖中線路游覽A,B,C三個景點及沿途風景,則不重復(除交匯點O外)的游覽線路有( )。

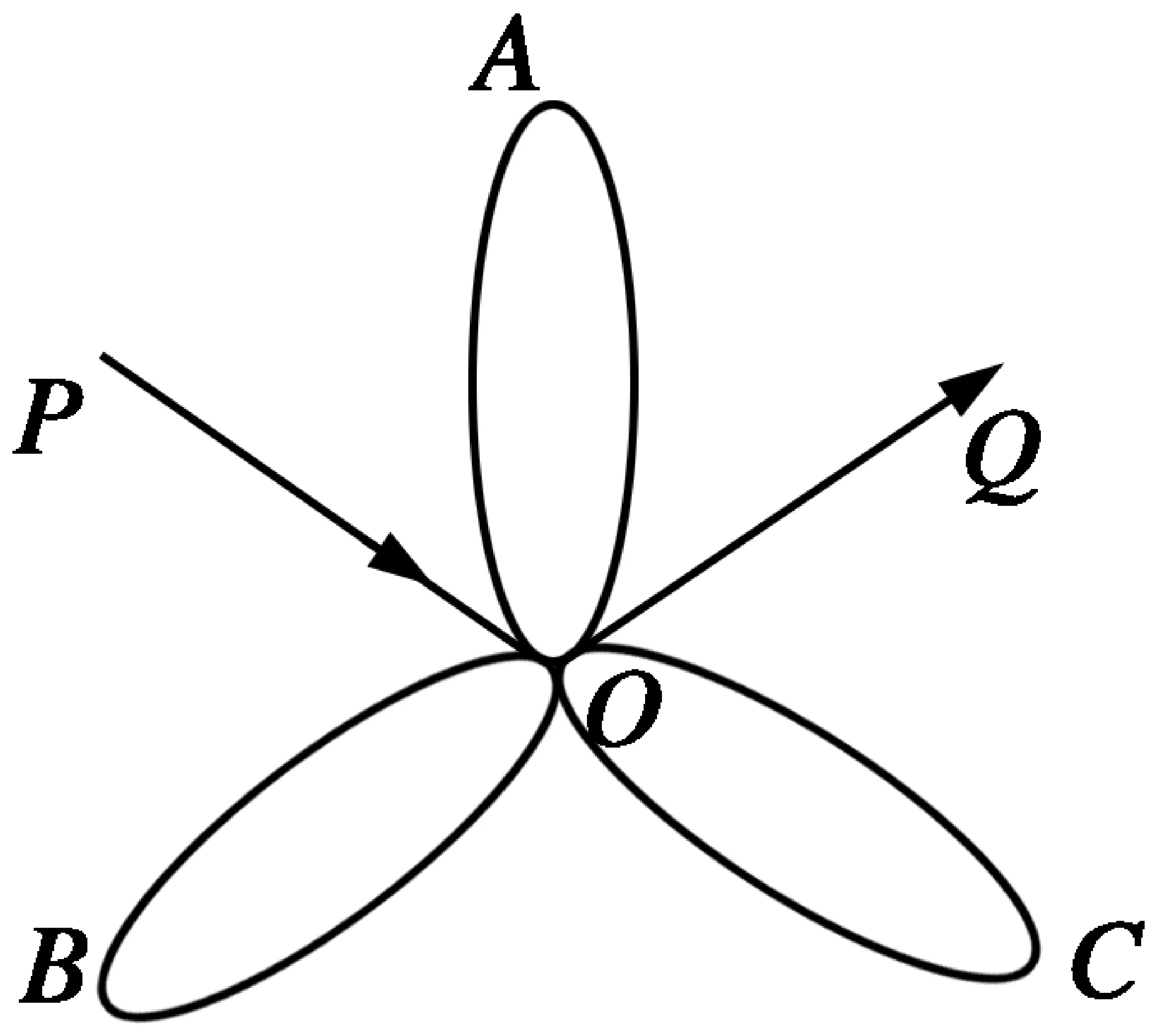
圖2

A.6種 B.8種

C.12種 D.48種

10.現有2門不同的考試要安排在5天之內進行,每天最多進行1門考試,且不能連續2天有考試,那么不同的考試安排方案種數是( )。

A.12 B.6 C.8 D.16

11.一排有6個座位,三位同學隨機就座,任意兩人不相鄰的坐法種數為( )。

A.12 B.36 C.24 D.72

12.安排6名歌手演出順序時,要求歌手乙、丙均排在歌手甲的前面或者后面,則不同排法的種數是( )。

A.180 B.240 C.360 D.480

13.用數字1,2,3,4,5組成沒有重復數字的五位數,其中奇數的個數為( )。

A.24 B.48 C.60 D.72

14.我們把各位數字之和為6的四位數稱為“六合數”(如2013是“六合數”),則首位為2的“六合數”共有( )。

A.18個 B.15個

C.12個 D.9個

15.從1,3,5,7,9這五個數中,每次取出兩個不同的數分別記為a,b,共可得到lga-lgb不同值的個數是( )。

A.9 B.10 C.18 D.20

16.從正方體六個面的對角線中任取兩條作為一對,其中所成的角為60°的共有( )。

A.24對 B.30對

C.48對 D.60對

17.將標號為1,2,3,4的4個籃球分給3位小朋友,每位小朋友至少分到一個籃球,且標號為1,2的2個籃球不能分給同一位小朋友,則不同的分法種數為( )。

A.15 B.20 C.30 D.42

18.現有2名男生,3名女生和1位老師共6人站成一排照相,若兩端站男生,3名女生中有且僅有2名相鄰,則不同的站法種數是( )。

A.12 B.24 C.36 D.48

19.某學校開設“藍天工程博覽課程”,組織6個年級的學生外出參觀包括甲博物館在內的6個博物館,每個年級任選1個博物館參觀,則有且只有2個年級選擇甲博物館的情況有( )。

A.A26×A45種 B.A26×54種

C.C26×A45種 D.C26×54種

20.由1、2、3、4、5、6組成沒有重復數字且1、3都不與5相鄰的六位偶數,則這樣的偶數的個數是( )。

A.72 B.96 C.108 D.144

21.從集合{1,2,3,4,…,10}中選出5個數組成子集,使得這5個數中任意2個數的和都不等于11,則這樣的子集有( )。

A.32個 B.34個

C.36個 D.38個

22.有5名優秀畢業生到母校的3個班級去作學習經驗交流,則每個班至少去1名的不同分派方法種數為( )。

A.150 B.180 C.200 D.280

23.有紅、藍、黃、綠四種顏色的球各6個,每種顏色的6個球分別標有數字1,2,3,4,5,6,從中任取3個標號不同的球,這3個顏色互不相同且所標數字互不相鄰的取法種數為( )。

A.80 B.84 C.96 D.104

24.將甲、乙、丙、丁、戊5位同學分別保送到北大、上海交大和浙大3所大學,若每所大學至少保送1人,且甲不能保送到北大,則不同的保送方案共有( )。

A.150種 B.114種

C.100種 D.72種

25.某微信群中甲、乙、丙、丁、戊5名成員同時搶4個紅包,每人最多搶1個紅包,且紅包全被搶光,4個紅包中有2個2元,2個3元,金額相同視為相同紅包,則甲、乙2人都搶到紅包的情況有( )。

A.36種 B.24種

C.18種 D.9種

26.某學校安排甲、乙、丙、丁4位同學參加數學、物理、化學競賽,要求每位同學僅報1科,每科至少有1位同學參加,且甲、乙不能參加同一學科,則不同的安排方法有( )。

A.36種 B.30種

C.24種 D.6種

27.如圖3所示的陰影部分由方格紙上3個小方格組成,我們稱這樣的圖案為L型(每次旋轉90°仍為L型圖案),那么在由4×5個小方格組成的方格紙上可以畫出不同位置的L型圖案的個數是( )。

A.16 B.32 C.48 D.64

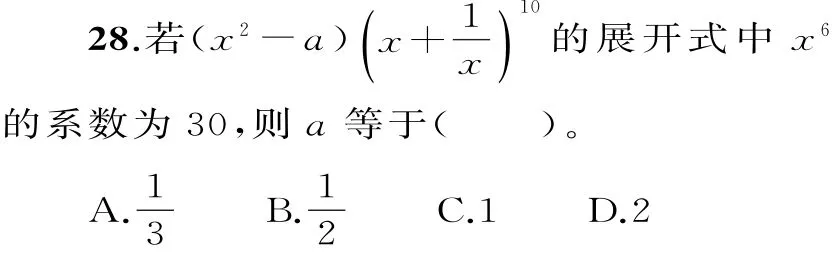
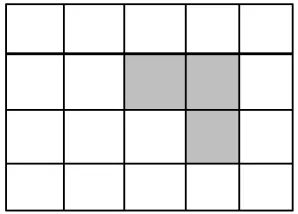
圖3

29.(x2+x+y)5的展開式中x5y2的系數為( )。

A.10 B.20 C.30 D.60

30.設的展開式的各項系數之和為M,二項式系數之和為N,若M-N=240,則展開式中x的系數為( )。

A.-150 B.150 C.300 D.-300

31.已知1120,其中實數a是常數,則展開式中各項系數的和是( )。

A.28B.38

C.1或38D.1或28

32.若第3項的二項式系數為36,則其展開式中的常數項為( )。

A.84 B.-252

C.252 D.-84

33.若項的二項式系數最大,則其展開式的常數項是( )。

A.360 B.180 C.90 D.45

34.已知(2x-1)3=a0+a1x+a2x2+a3x3,則a0+a2等于( )。

A.-13 B.-10 C.10 D.13

35.在1+(1+x)+(1+x)2+(1+x)3+(1+x)4+(1+x)5的展開式中,含x2項的系數是( )。

A.10 B.15 C.20 D.25

36.若(x2+1)(x-3)9=a0+a1(x-2)+a2(x-2)2+a3(x-2)3+…+a11(x-2)11,則a1+a2+…+a11的值為( )。

A.0 B.-5 C.5 D.255

37.設a,b,m為整數(m＞0),若a和b被m除得的余數相同,則稱a和b對模m同余,記a≡b(modm)。若a=C118+C218+…+,a≡b(mod9),則b的值可以是( )。

A.2015 B.2016

C.2017 D.2018

38.在(1+x)6(1+y)4的展開式中,記xmyn項的系數為f(m,n),則f(3,0)+f(2,1)+f(1,2)+f(0,3)=( )。

A.45 B.60 C.120 D.210

39.現定義eiθ=cosθ+isinθ,其中i為虛數單位,e為自然對數的底數,θ∈R,且實數指數冪的運算性質對eiθ都適用。若a=,那么復數a+bi等于( )。

A.cos5θ+isin5θ B.cos5θ-isin5θ

C.sin5θ+icos5θ D.sin5θ-icos5θ

二、填空題

40.在三位正整數中,若十位數字小于個位和百位數字,則稱該數為“駝峰數”。比如“102”,“546”為“駝峰數”,由數字1,2,3,4可構成無重復數字的“駝峰數”有____個。

41.5名學生報名參加四項體育比賽,每人限報一項,則不同的報名方法的種數為____。5名學生爭奪四項比賽的冠軍(冠軍不并列),則獲得冠軍的可能性有____種。

42.直線Ax+By=0,若從集合E={0,1,3,5,7,8}中每次取出2個不同的數作為A,B的值,則可表示____條不同的直線。

43.現有2個紅球,3個黃球,4個白球,同色球不加區分,將這9個球排成一列,有____種不同的排列方法。

44.在數字1,2,3與符號“+”“-”這5個元素的所有全排列中,任意2個數字都不相鄰的全排列方法共有____種。

45.國家教育部為了發展貧困地區教育,在全國重點師范大學免費培養教育專業師范生,畢業后要分到相應的地區任教。現有6位免費培養的教育專業師范畢業生要平均分到3所學校去任教,則有____種不同的分派方法。

46.若把英語單詞“error”的字母順序寫錯了,則可能出現的錯誤共有____種。

47.用字母A,Y,數字1,8,9構成一個字符不重復的五位號牌,要求字母A,Y不相鄰,數字8,9相鄰,則可構成的號牌的個數是____。

48.如果把個位數是1,且恰有3個數字相同的四位數叫作“好數”,那么在由1,2,3,4四個數字組成的有重復數字的四位數中,“好數”共有____個。

49.化簡

50.在(2x+x)5的展開式中,x3的系數是____。

51.1.028的近似值是____。(精確到小數點后三位)

52.已知(x+2y)n的展開式中第二項的系數為8,則(1+x)+(1+x)2+…+(1+x)n展開式中所有項的系數和為____。

53.(1+x+x2)常數項為____。

54.(x-y)(x+y)8的展開式中x2y7的系數為____。

55.設復數____。

56.若(2x+3)3=a0+a1(x+2)+a2(x+2)2+a3(x+2)3,則a0+a1+2a2+3a3=____。

57.若(x+2+m)9=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9,且(a0+a2+…+a8)2-(a1+a3+…+a9)2=39,則實數m的值為____。

三、解答題

58.編號為A,B,C,D,E的5個小球放在如圖4所示的5個盒子里,要求每個盒子只能放1個小球,且A球不能放在1,2號,B球必須放在與A球相鄰的盒子中,則不同的放法有多少種?

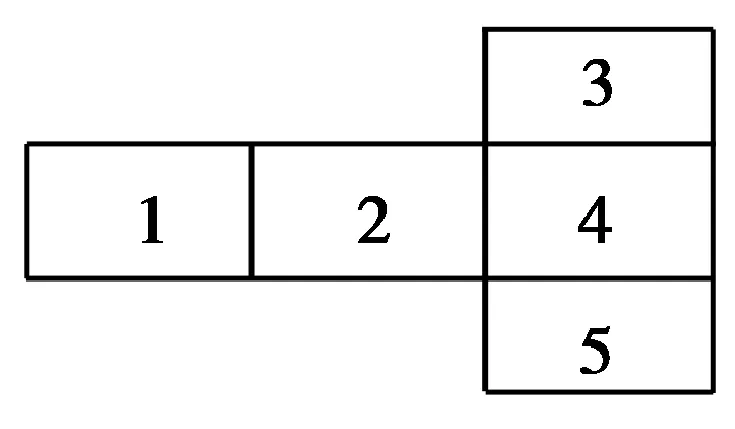
圖4

59.用0,1,2,3,4,5,6構成無重復數字的七位數。

(1)能被25整除的數有多少個?

(2)設x,y,z分別表示個位、十位、百位上的數字,滿足x＜y＜z的數有多少個?

(3)偶數必須相鄰的數有多少個?

60.有6名學生報名參加3個智力競賽項目,在下列情況下各有多少種不同的報名方法?(不一定6名學生都能參加)

(1)每人恰好參加1項,每項人數不限;

(2)每項限報1人,且每人至多參加1項;

(3)每項限報1人,但每人參加的項目不限。

61.已知集合A={a1,a2,a3,a4},B={0,1,2,3},f是從集合A到集合B的映射。

(1)若B中每一個元素都有原象,這樣不同的f有多少個?

(2)若B中的元素0無原象,這樣的f有多少個?

(3)若f滿足f(a1)+f(a2)+f(a3)+f(a4)=4,這樣的f有多少個?

62.某醫院有內科醫生12名,外科醫生8名,現選派5名參加賑災醫療隊,其中:

(1)某內科醫生甲與某外科醫生乙必須參加,共有多少種不同選法?

(2)甲、乙均不能參加,有多少種選法?

(3)甲、乙2人至少有1人參加,有多少種選法?

(4)隊中至少有1名內科醫生和1名外科醫生,有幾種選法?

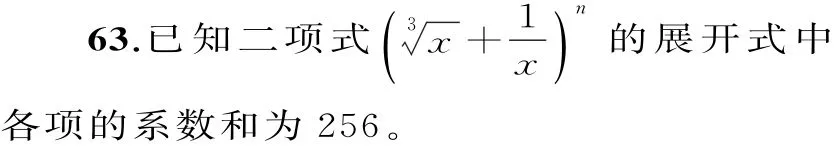
(1)求n;

(2)求展開式中的常數項。

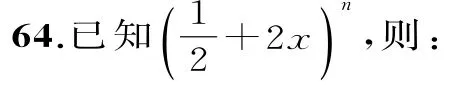
(1)若展開式中第5項,第6項與第7項的二項式系數成等差數列,求展開式中二項式系數最大項的系數;

(2)若展開式前三項的二項式系數和等于79,求展開式中系數最大的項。

(1)展開式中所有含x的有理項;

(2)展開式中系數最大的項。

66.已知(1-2x)7=a0+a1x+a2x2+…+a7x7,求:

(1)a1+a2+…+a7;

(2)a1+a3+a5+a7;

(3)a0+a2+a4+a6;

(4)|a0|+|a1|+|a2|+…+|a7|。