平面向量常見典型考題賞析

■余智敏 何春玲

題型1：平面向量的基本概念

求解與平面向量的概念有關的命題的真假判定問題，關鍵在于理解平面向量的概念，還應注意零向量的特殊性以及兩個向量相等必須滿足:模相等且方向相同。向量與數量不同，數量可以比較大小，向量不能比較大小，但向量的模是非負實數，可以比較大小。

例 1給出下列四個命題:

①若|a|=|b|，則a=b；②若A，B，C，D是不共線的四點，則是四邊形ABCD為平行四邊形的等價條件；③若a=b，b=c，則a=c；④a=b 的等價條件是|a|=|b|且a∥b。

其中正確命題的序號是( )。

A.②③ B.①②

C.③④ D.①④

解：兩個向量的長度相等，但它們的方向不一定相同，①不正確。由，可得，又A，B，C，D是不共線的四點，可知四邊形ABCD為平行四邊形；反之，若四邊形ABCD為平行四邊形，則，②正確。由a=b，可得a，b的長度相等且方向相同，由b=c，可得b，c的長度相等且方向相同，所以a，c的長度相等且方向相同，即a=c，③正確。當a∥b且方向相反時，即使|a|=|b|，也不能得到a=b，故|a|=|b|且a∥b不是a=b的等價條件，④不正確。應選A。

跟蹤訓練1：給出下列四個命題:

①兩個具有公共終點的向量，一定是共線向量；②兩個向量不能比較大小，但它們的模能比較大小；③λ a=0(λ為實數)，則λ必為零；④已知λ，μ為實數，若λ a=μb，則a與b共線。

其中錯誤的命題個數為( )。

A.1 B.2

C.3 D.4

提示：兩向量共線要看其方向而不是起點或終點，①錯誤。因為向量既有大小，又有方向，故它們不能比較大小，但它們的模均為非負實數，可以比較大小，②正確。當a=0時，不論λ為何值，λ a=0，③錯誤。當λ=μ=0時，λ a=μb=0，此時，a與b可以是任意向量，④錯誤。應選C。

題型2：共線向量定理及其應用

(1)利用共線向量定理可以證明向量共線，也可以由向量共線求參數的值。(2)若a，b不共線，則λ a+μb=0的等價條件是λ=μ=0，這一結論結合待定系數法應用非常廣泛。(3)證明三點共線的方法:若存在實數λ，使得，則A，B，C三點共線。

例 2設兩個非零向量a和b不共線。

(1)若3(a-b)，求證:A，B，D三點共線。

(2)試確定實數k的值，使k a+b與a+k b共線。

解：(1)因為=2a+8b，=2a+8b+3(a-b)=5(a+b)=5，由此可知共線。

又有公共點B，所以A，B，D三點共線。

(2)因為k a+b與a+k b共線，所以存在實數λ，使得k a+b=λ(a+k b)，即得解得k=±1。故當k=±1時，k a+b與a+k b共線。

跟蹤訓練2：已知a，b是兩個不共線的非零向量，且a與b起點相同。若a，t b，(a+b)這三個向量的終點在同一條直線上，則t=____。

題型3：平面向量基本定理的應用

平面向量基本定理表示向量的實質是利用平行四邊形法則或三角形法則進行向量的加、減或數乘運算。利用平面向量基本定理解決向量問題的一般思路是:先選擇一組基底，并運用該基底將條件和結論表示成向量的形式，再通過向量的運算來解決問題。

例3如圖1，在△ABC中，設=a，=b，AP的中點為Q，BQ的中點為R，CR的中點恰為P，則=( )。

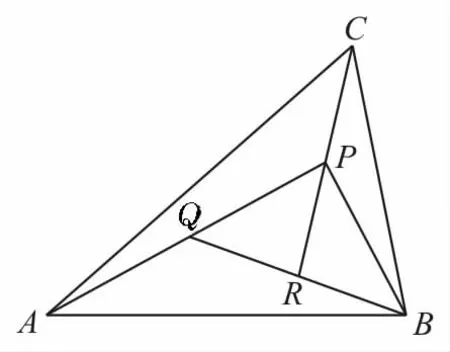
圖1

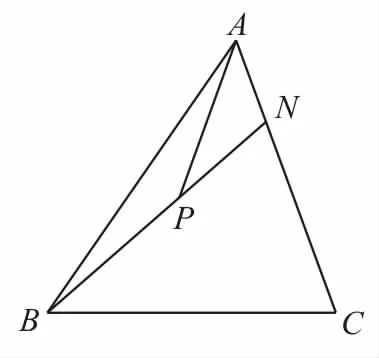
圖2

題型4：平面向量的數量積

向量數量積的兩種運算方法:①當已知向量的模和夾角時，可利用定義法求解，即a·b=|a||b|cos〈a，b〉；②當已知向量的坐標時，可利用坐標法求解，即若a=(x1，y1)，b=(x2，y2)，則a·b=x1x2+y1y2。

向量數量積的運算要注意兩點:①若a·b=a·c(a≠0)，則不一定得到b=c；②向量數量積的運算不滿足乘法結合律，即(a·b)·c不一定等于a·(b·c)。

例 4如圖3，在△ABC中，D是BC的中點，E，F是AD上的兩個三等分點，____。

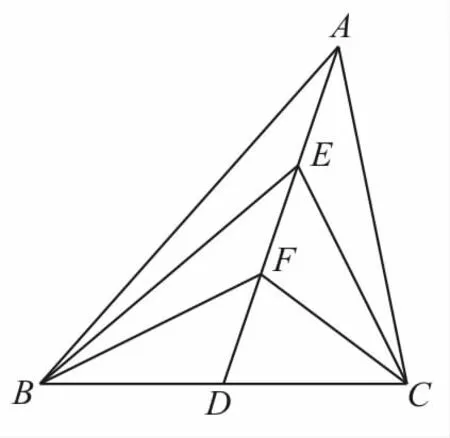
圖3

解：(方法1)以D為坐標原點，BC所在的直線為x軸，線段BC的中垂線為y軸，建立平面直角坐標系x Dy(圖略)。

跟蹤訓練4：如圖4，正方形ABCD的邊長為1，點E是AB邊上的動點，則的值為____，的最大值為____。

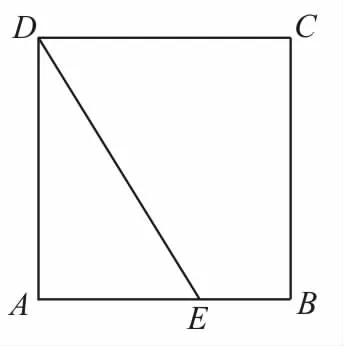
圖4

(方法2)以A為坐標原點，AB，AD分別為x軸，y軸，建立平面直角坐標系x Ay(如圖5)。

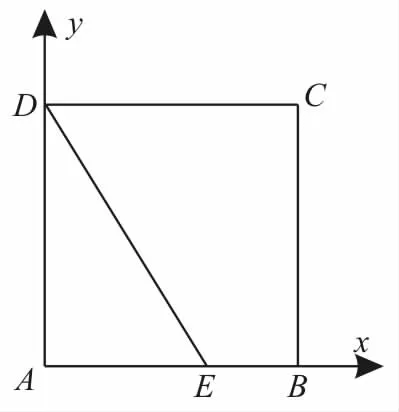
圖5

則 A(0，0)，B(1，0)，C(1，1)，D(0，1)。

設E(t，0)，t∈[0，1]，則=(t，-1)，=(0，-1)，可得=(t，-1)·(0，-1)=1。

由DC→=(1，0)，得=(t，-1)·(1，0)=t≤1，即的最大值為1。

(方法3)如圖6，無論點E在哪個位置，方向上的投影都是||=1，可得|·1=1。

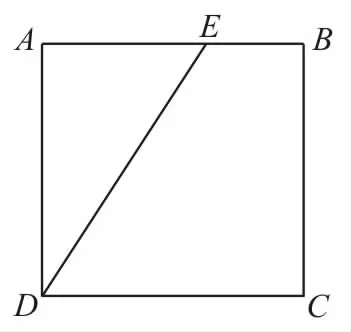
圖6

當點E運動到點B時，方向上的投影最大，其最大值為||=1，可得|·1=1。

題型5：平面向量的夾角

求向量的夾角的常見題型:①依據條件等式求兩向量的夾角，此類問題求解過程中應關注夾角的取值范圍；②依據已知圖形求兩向量的夾角，此類問題求解過程中應抓住“兩向量共起點”的特點。

求兩個非零向量的夾角要注意:①數量積大于0，說明不共線的兩個向量的夾角為銳角；②數量積等于0，說明兩個向量的夾角為直角；③數量積小于0且兩個向量不共線時，兩向量的夾角是鈍角。

例 5若向量a，b的夾角為，且|a|=2，|b|=1，則a與a+2b的夾角為( )。

解：設向量a與a+2b的夾角為α。

跟蹤訓練5：已知兩個單位向量a，b的夾角為60°，c=t a+(1-t)b。若b·c=0，則t=。

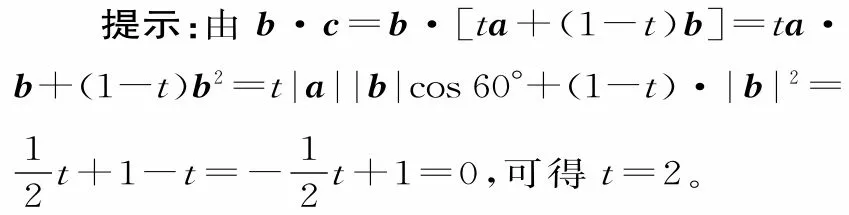
題型6：平面向量的模

把向量放在適當的坐標系中，給有關向量賦予具體坐標求向量的模，如向量a=(x，y)，則|a|=。不把向量放在坐標系中，求向量的模，這時可利用公式|a|=及(a±b)2=|a|2±2a·b+|b|2轉化求解。

解：由題意可得|e1|=1，|e2|=1。由得〈e1，e2〉=60°。

由b·e1=b·e2=1＞0，可得〈b，e1〉=〈b，e2〉=30°。

由b·e1=1，可得|b||e1|cos 30°=1，故

題型7：平面向量的共線與垂直問題

平面向量的坐標表示可使平面向量的運算完全代數化，于是可利用“方程的思想”求解向量的共線與垂直問題。

跟蹤訓練7：已知向量a=(3，1)，b=(1，3)，c=(k，-2)，若(a-c)∥b，則向量a與c的夾角的余弦值是( )。

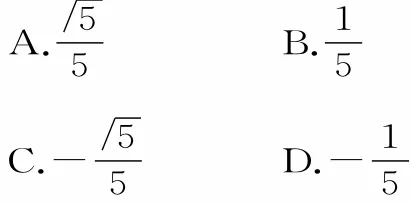
提示：由已知得a-c=(3-k，3)。

由(a-c)∥b，可得3(3-k)-3=0，解得k=2，這時c=(2，-2)。

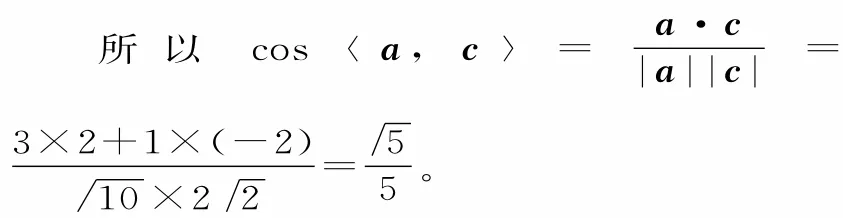
題型8：向量在解析幾何中的應用

向量在解析幾何中的作用:①載體作用，向量在解析幾何問題中出現，多用于“包裝”，解決此類問題的關鍵是利用向量的意義、運算，脫去“向量外衣”。②工具作用，利用a⊥b?a·b=0，a∥b?a=λ b(b≠0)，可解決垂直、平行問題。

例8(1)已知向量(4，5)，=(10，k)，且A，B，C三點共線，當k＜0時，若k為直線的斜率，則過點(2，-1)的直線方程為____。

(2)設O為坐標原點，C為圓(x-2)2+y2=3的圓心，且圓上有一點M(x，y)滿足=____。

解：(1)由=(4-k，-7)，=(6，k-5)，且，可得(4-k)(k-5)+6×7=0，解得k=-2或k=11。

由k＜0，可知k=-2，則過點(2，-1)且斜率為-2的直線方程為y+1=-2(x-2)，即2x+y-3=0。

(2)由=0，可得OM⊥CM，可知OM是圓的切線。

設OM的方程為y=k x。

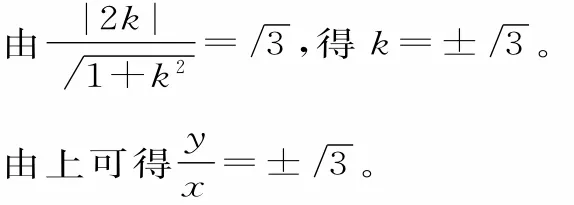
跟蹤訓練8：已知圓C:(x-2)2+y2=4，圓M:(x-2-5cosθ)2+(y-5sinθ)2=1(θ∈R)，過圓M 上任一點P作圓C的兩條切線P E，P F，切點分別為E，F，則P→E·P→F的最小值是( )。

A.5 B.6

C.10 D.12

提示：由圓C:(x-2)2+y2=4，可知圓心C(2，0)，半徑為2。

由圓M:(x-2-5cosθ)2+(y-5sinθ)2=1，可知圓心 M(2+5cosθ，5sinθ)，半徑為1。由于CM==5＞2+1，所以圓C與圓M相離。

如圖7所示，設直線CM 和圓M 交于H，G兩點，則的最小值是。

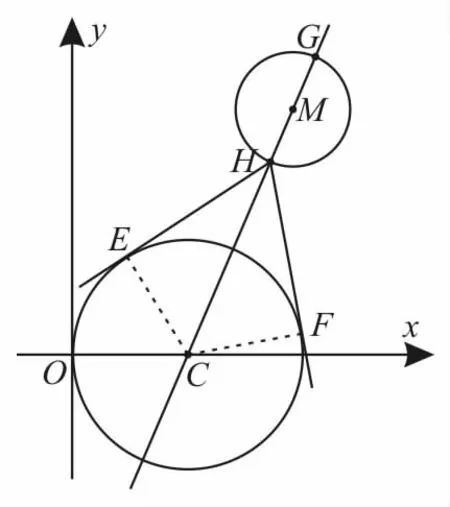
圖7

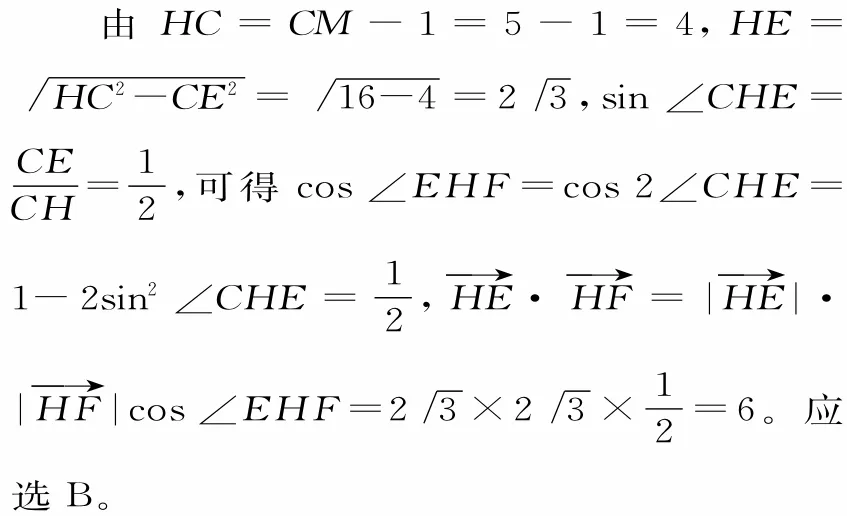
題型9：平面向量與三角函數的交匯問題

平面向量與三角函數的交匯問題是近幾年高考的熱點，應該引起同學們的重視。

(1)若m⊥n，求tanx的值。

提示：由題意可知6sin2α+cosα(5sinα-4cosα)=0，即 6sin2α+5sinαcosα-4cos2α=0。

上述等式兩邊同除以cos2α，得6tan2α+5tanα-4=0。

題型10：平面向量中的新定義問題

這類問題的特點是背景新穎，信息量大，通過它可考查同學們獲取信息，利用信息分析和解決問題的能力。解答這類問題，首先要分析新定義的特點，把新定義所敘述的問題的本質弄清楚，然后應用到具體的解題過程中，這是破解新定義信息問題難點的關鍵。

例10對任意兩個非零的平面向量α向量a，b滿足a與b的夾角b等于( )。

跟蹤訓練10：設向量a=(a1，a2)，b=(b1，b2)，定義一種向量積a?b=(a1b1，P(x，y)在y=sinx的圖像上運動，Q是函數y=f(x)圖像上的點，且滿足=m?+n(其中O為坐標原點)，則函數y=f(x)的值域是____。

提示：設點Q(c，d)。

由點P(x，y)在y=sinx的圖像上，可知點P(x，sinx)。