兩種典型低空風切變對火箭彈彈道特性的影響

陳健偉， 王良明， 李子杰

(南京理工大學 能源與動力工程學院， 南京 210094)

風切變是一種廣泛存在的大氣現(xiàn)象，其表現(xiàn)為大氣中任意兩點間風速和風向的突然變化，包括水平風切變(同一高度)和垂直風切變(不同高度)。高度600 m以內發(fā)生的風切變定義為低空風切變。低空風切變現(xiàn)象的形成通常伴隨著強烈對流性或鋒面活動頻繁的天氣，同時也與周邊環(huán)境、地理地形等有著密切聯(lián)系[1]。若飛行器運動途經(jīng)低空風切變區(qū)域，則該區(qū)域內風速的劇烈變化會改變飛行器的受力狀態(tài),從而影響其飛行穩(wěn)定性和飛行軌跡。火箭彈在發(fā)射初始階段，尤其是剛脫離定向器時，運動速度小，抗擾動能力弱，變化劇烈的風場可引起較大的距離和方向偏差[2]。如何考慮和較為真實地反映低空風切變對火箭彈飛行過程和彈道特性的影響，對于火箭彈的發(fā)射控制有著重要意義。

變化風場對火箭彈飛行過程的影響一直以來是彈道學研究中的一個重要問題，而對其中的風切變現(xiàn)象，所展開的研究則較為有限。文獻[3]基于外彈道學及氣象學理論建立了不同風場下彈丸的飛行動力學模型，并分析了不同風場對彈丸彈道特性的影響。在風切變風場建模方面，文獻[4]提出了2種低空風切變的簡化模型，并研究了低空風切變對飛行器掠地飛行的影響。文獻[5]基于BRAMS(Brazilian developments on the Regional Atmospheric Modeling System)模型建立了垂直風切變的風廓線模型。文獻[6-7]采用渦環(huán)法構建了微下?lián)舯┝鞯娘L場模型。文獻[8]在文獻[6-7]所建模型的基礎上考慮了微下?lián)舯┝黠L場中湍流效應。文獻[9]以歐洲天氣預報中心30年數(shù)據(jù)為基礎，提出了基于統(tǒng)計數(shù)據(jù)的低空急流識別模型。文獻[10]提出了一種適用于沿海地區(qū)的新型中尺度低空急流預報模型。文獻[11-13]對中國低空急流風切變的識別探測及數(shù)值仿真研究進展進行了綜述。

目前對于低空風切變的相關研究主要集中在低空風切變的檢測識別以及危害防范方面，而對于低空風切變這一大氣現(xiàn)象對火箭彈飛行過程的影響這一問題的探究較少。基于此，本文采用數(shù)值仿真的方法研究分析2種典型的低空風切變作用下，火箭彈彈道特性的變化情況，并分析不同風場特征參數(shù)對其彈道特性的影響規(guī)律，以期為火箭彈的彈道研究及發(fā)射控制提供一定的參考。

1 低空風切變風場模型

不同形式的風切變具有不同的時間和空間特征[14]，對火箭彈飛行的影響嚴重程度也不同。綜合考慮多項因素，本文選取2種形成概率高、危害尺度大的典型風切變形式：微下?lián)舯┝骱偷涂占绷鬟M行建模分析。

1.1 微下?lián)舯┝髂Ｐ?/h3>

作為一種常見的低空風切變現(xiàn)象，微下?lián)舯┝鞯男纬赏ǔＥc對流風暴有關，其形成于強對流云團內，從云底部產生一股局部性垂直向下氣流，下沉后與地面碰撞變?yōu)檩椛⒒蛑本€型地面氣流[14],形成過程如圖1所示。目前針對微下?lián)舯┝鞯墓こ袒Ｐ椭饕信紭O子模型和渦環(huán)模型[15]，為簡化仿真流程、降低模型計算復雜度，在保證風場空間特性的基礎上，選取渦環(huán)模型來構建微下?lián)舯┝黠L場模型。

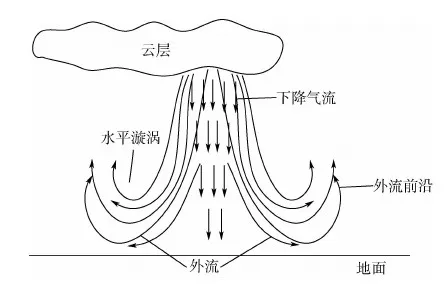
圖1 微下?lián)舯┝鞯男纬蛇^程Fig.1 Forming process of microburst

以地面坐標系為參考系，配置渦環(huán)模型，其中Oxyz為地面坐標系，以地面上方點OP為中心，建立半徑為R的主渦環(huán)，如圖2所示，主渦環(huán)曲線方程為

(1)

式中：(xP,yP,zP)為點OP在地面坐標系中的坐標。

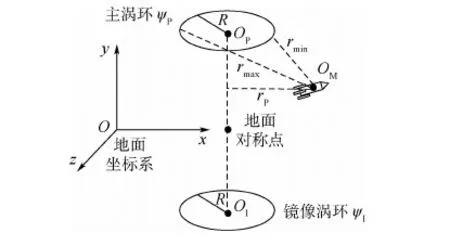
圖 2 渦環(huán)模型示意圖Fig.2 Schematic diagram of vortex ring model

主渦環(huán)流線方程為[6]

(2)

式中：Γ為渦環(huán)強度，由渦環(huán)中心垂直速度Vz(0)和渦環(huán)半徑R確定[6]

Γ=2RVz(0)

(3)

rmax和rmin分別為空間中任意一點OM(xM,yM,zM)到主渦環(huán)的最大和最小距離；F(k)為橢圓積分函數(shù)，k定義為[6]

(4)

當0≤k≤1時，F(xiàn)(k)可近似為[6]

(5)

由渦環(huán)流線方程可以求出渦環(huán)徑向(平行于水平面)和軸向(平行于Oz軸)的誘導速度分別為

(6)

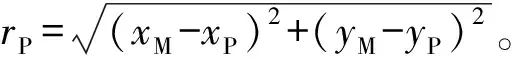
(7)

圖2中，在主渦環(huán)關于水平面(xOz平面)對稱的位置設置一鏡像渦環(huán)，2個渦環(huán)的中心Op和OI(xp,yp,-zp)連線垂直于xOz平面。這一設置是因為實際情況下，氣流到達地面后沿水平方向擴散，其垂直方向風速應為0，由于鏡像渦環(huán)流線方程ψI與主渦環(huán)流線方程形式相同、符號相反：ψI=-ψP，因此兩渦環(huán)產生的誘導速度在地面處同值反向，相互抵消。根據(jù)鏡像渦環(huán)的流線方程，推導出其在空間任意點的誘導風速，根據(jù)疊加原理結合式(6)和式(7)即可計算出點OM處的合速度：

(8)

則空間內任一點OM的流線方程可表示為[6]

(9)

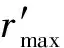
在上述建模過程中，需考慮以下情形：

1)OPOI連線上的點(符合rP=0)，根據(jù)流線方程計算得到的誘導速度趨近于+，不符合實際，因此該直線上的誘導速度由渦環(huán)位函數(shù)求偏導獲得

(10)

2) 渦環(huán)線上的點(符合rP=R，zM=zP), 根據(jù)流線方程計算得到的誘導速度也趨近于+，不符合實際。因此，文獻[16]提出的方法：以渦環(huán)線上的點為圓心，構造半徑為r的封閉環(huán)形圓柱，渦量在該環(huán)形圓柱中均勻分布，渦環(huán)線上的點誘導速度為0，環(huán)形圓柱外側的點滿足流線方程ψP，由渦環(huán)線至環(huán)形圓柱外側，誘導速度呈線性分布。流速分布情況見圖3。

當點OM位于環(huán)形圓柱內時，聯(lián)合(x-xP)2+(y-yP)2=R2和直線OPOM在水平面內的投影直線方程，即可推導計算出點M的坐標PM，進一步，環(huán)形圓柱外側點N的坐標PN為

(11)

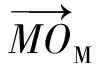
(12)

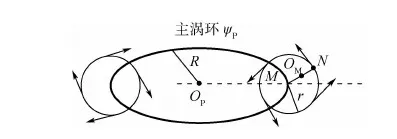
圖 3 環(huán)形圓柱內風矢量示意圖Fig.3 Schematic diagram of wind vector in annular cylinder

1.2 低空急流模型

邊界層急流主要指對流層下層中的強風帶，是一種在穩(wěn)定的地面邊界層內發(fā)生的地面逆溫現(xiàn)象[17]。基于流體力學中平面壁面射流原理[18]，結合低空平均風剖面建立邊界層急流模型。

根據(jù)流體力學相關理論，某一射流在水平方向的分速度u(x,H)和該射流的速度幅值um(x)滿足如下條件：

(13)

式中：H為高度。

假設沿水平方向x的速度分布是均勻的，又可寫成

(14)

式中：Hs為表征對稱分布的自由射流的最大速度高度；Cs為射流形狀參數(shù)，表征Hs與射流豎直方向厚度B的關系。其中，自由射流的厚度定義為垂直高度內，大于射流速度幅值7%的速度分布范圍，表達式為

(15)

在邊界層的平均風廓線(指數(shù)風廓線)基礎上，加上已推導的射流速度分布關系式，整理合并得垂直方向上低空急流速度分布的表達式為

(16)

式中：uR為參考高度HR上對應的風速；文獻[19]中根據(jù)中國風資料確定的指數(shù)mp的計算公式為

mp=1/ln((Z2Z1)0.5/Z0)-0.040 3ln(uR/6)

(17)

式中：Z0為地面粗糙度；Z1=HR;Z2為實際高度。

對于地面邊界層中急流的矢量切變，按照風速模型中類似的疊加方式進行建模，可得高度H相對高度H0處的風向偏差近似為

(18)

式中：H0、HL、HT分別為基準高度、急流層內風向偏差最大處高度、急流層頂高度；αH0、αHL、αHT分別為3個高度對應處的風向與地轉風之間的夾角；CL為射流形狀參數(shù)，表征HL與射流豎直方向厚度B的關系，其計算方法可類比于Cs。

1.3 仿真驗證

本節(jié)通過數(shù)值仿真的方法，獲取風場模型計算結果，并與相關資料中實測風切變風場分布情況進行對比。設置2種風切變風場的模型參數(shù)如表1、表2所示。其中，表2中風向均指對應高度處風向與地轉風風向的夾角，同時，仿真時假設急流層內，最大風速與最大風向偏差出現(xiàn)在同一高度。

按表1和表2設置的參數(shù)進行風場計算仿真，微下?lián)舯┝黠L場分布情況如圖4、圖5所示。

由圖4可以看出，渦環(huán)中心軸附近區(qū)域，風速垂直分量較大，沿水平方向，距離渦環(huán)中心軸越遠風速越小。由圖5可以看出。水平剖面內，渦環(huán)中心附近為風速極值區(qū)，風速沿渦環(huán)中心向四周呈輻射狀衰減分布。

表1 微下?lián)舯┝髂Ｐ蛥?shù)

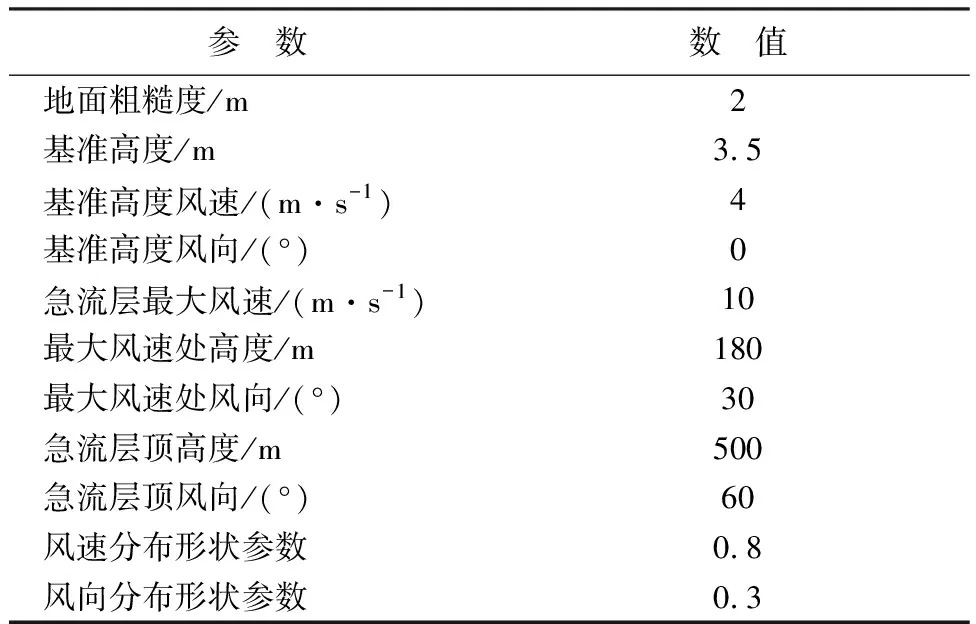
表2 低空急流模型參數(shù)

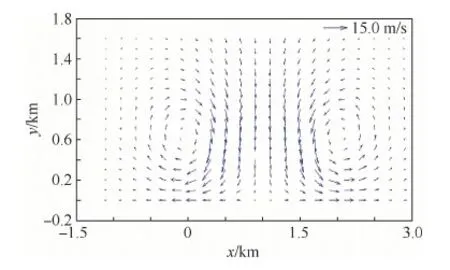
圖4 渦環(huán)中心垂直剖面風矢量圖Fig.4 Wind vector diagram of vertical section of vortex ring center

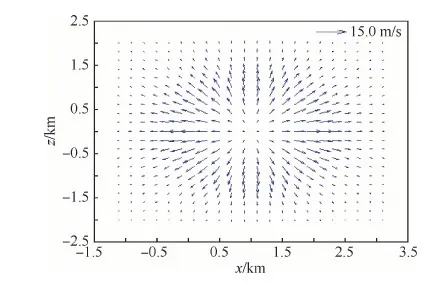
圖5 y=100 m水平剖面風矢量圖Fig.5 Wind vector diagram of horizontal section (y=100 m)

通過圖4、圖5與圖6[20]、圖7[21]實測風場數(shù)據(jù)的比較可以看出，基于渦環(huán)法的風場模型能夠較為真實地反映微下?lián)舯┝鞯膶嶋H風速分布情況，模型空間特征合理，滿足彈道仿真的要求。

圖8為低空急流風場仿真結果，通過圖8與圖9[17]某次低空急流實測風場數(shù)據(jù)的比較可以看出，基于平面壁面射流原理的風場模型仿真得出的風速風向隨高度分布與實測風場在趨勢上基本一致，該模型能夠在一定程度上反映低空急流風切變的風場特性。

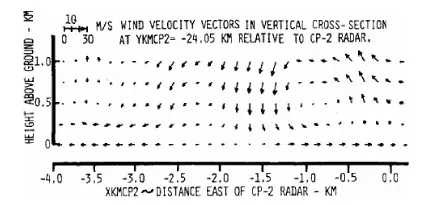
圖6 1982年JAWS計劃實測微下?lián)舯┝黠L切變風場特征圖[20]Fig.6 Wind field features of 1982 JAWS wind shear data showing a microburst flow pattern[20]

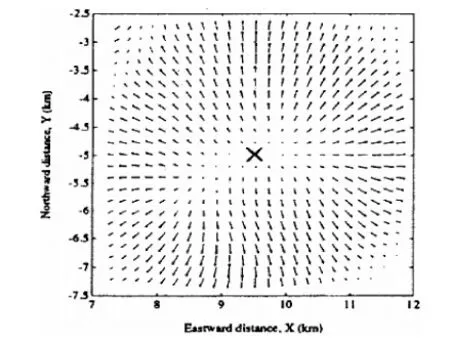
圖7 NASA 1988年美國丹佛微下?lián)舯┝魇鹿曙L場圖[21]Fig.7 Wind field of 1988 microburst event in Denver of US by NASA[21]

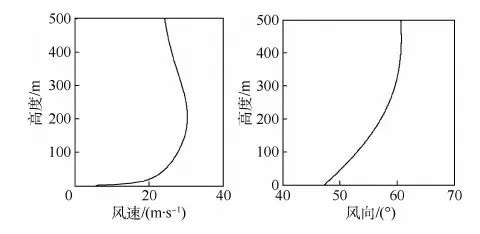
圖8 低空急流風場仿真結果Fig.8 Wind field simulation results of low-level jet

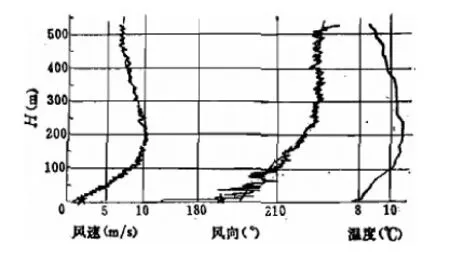
圖9 低空急流實際測量數(shù)據(jù)[17]Fig.9 Actual measurement data of low-level jet[17]

2 火箭彈剛體彈道模型

火箭彈作為自由剛體的，其運動過程由質心運動和繞質心運動兩部分組成。根據(jù)外彈道學理論[22]，選取合理的參考坐標系對火箭彈進行受力分析，在建立火箭彈運動方程時，將其當作常質量物體來處理。同時，忽略燃氣慣性力及其力矩，不考慮因火藥燃燒造成的質心移動加速度和轉動慣量變化率的影響。

忽略地球自轉等次要因素的影響，在彈道坐標系內分解火箭彈質心運動矢量方程，在彈軸坐標系內分解投影得到標量化的火箭彈繞心運動方程組。以慣性坐標系為參考，火箭彈的質心運動規(guī)律滿足質心運動定理：

(19)

式中：t為彈丸飛行時間；m為彈丸質量；v為火箭彈質心速度矢量；火箭彈質心所受合力F在彈道坐標系下的分量依次為Fx2、Fy2、Fz2。將式(19)向彈道坐標系投影，則可得到質心運動方程在彈道坐標系中的標量方程，即

(20)

式中：θ1為速度高低角;ψ2為速度方位角。

式(20)確定了火箭彈質心速度的大小與方向變化和作用在彈上的力之間的關系。描述火箭彈質心位置坐標變化的質心運動方程如下：

(21)

式中:(X,Y,Z)為火箭彈質心在地面坐標系下的坐標。彈丸的繞心運動由動量矩定理確定，即

(22)

式中：G為火箭彈相對于其質量中心的角動量；M為火箭彈受到合外力相對其質心的力矩。將式(22)向彈軸坐標系投影，略去部分小量，得到火箭彈繞質心運動的動力學方程和運動學方程分別為

(23)

(24)

式中：ωξ、ωη、ωζ為火箭彈轉動角速度在彈軸坐標系下分量；C和A分別為火箭彈的極轉動慣量和赤道轉動慣量；Mξ、Mη、Mζ為火箭彈所受外力矩在彈軸坐標系下分量；φa和φ2分別為彈軸高低角和彈軸方位角；γ為火箭彈自轉角。

考慮風的影響時，速度坐標系下作用在火箭彈上的力F2可以表示為火箭彈相對空氣的速度的函數(shù)：

F2=f(v-ω2)

(25)

式中：ω2為速度坐標系內的風速矢量，當獲得地面坐標系下風速分量大小ωx、ωz時，可通過式(26)求得風速矢量在速度坐標系內的分量大小ωx2、ωy2、ωz2，進而代入式(21)進行彈道解算。

(26)

實際情況下，火箭彈主動段火藥燃燒使得彈體總質量不斷減小，因此按火藥勻速率燃燒的情況來考慮火箭彈質量變化，即主動段內，火箭彈總質量變化微分方程為

(27)

式中：mb為火箭彈火藥質量燃燒速率，主動段結束后mb=0。

將式(20)、式(21)和式(23)、式(24)、式(27)聯(lián)立，即可得到描述火箭彈運動過程的6自由度剛體彈道方程，通過積分的方法求得火箭彈在任意時刻的運動狀態(tài)和對應的彈道諸元[23]。

3 仿真分析

將火箭彈的6自由度剛體彈道模型與2種典型風切變的風場模型相結合，探究不同風場條件下火箭彈飛行時間、射程、側偏和落速等彈道特性的變化規(guī)律。

以某122 mm尾翼火箭彈為例進行仿真計算。其彈體基本參數(shù)和發(fā)射初始條件分別如表3、表4所示，發(fā)動機工作的時間內火箭彈質量按勻速率減小考慮，轉動慣量和質心位置均相應隨時間勻速率變化。仿真中，除風場分布外的其他氣象條件均按照炮兵標準氣象條件[22]進行設置。

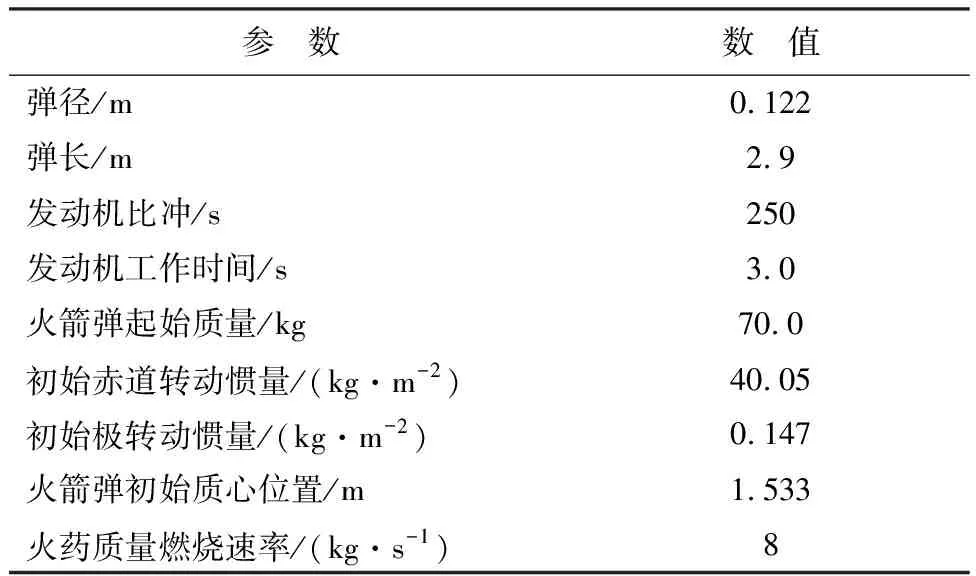
表3 火箭彈彈體參數(shù)

表4 火箭彈發(fā)射條件

3.1 微下?lián)舯┝鲗鸺龔棌椀捞匦杂绊?/h3>

為了簡化模型、便于分析，本文所建立的渦環(huán)模型未考慮風場強度的時變衰減以及渦環(huán)不對稱等情形。基于渦環(huán)法的風場模型中，中心垂直誘導風速反映了微下?lián)舯┝鞯膹姸龋鴾u環(huán)半徑大小則是風場空間尺度的決定性因素，因此，選取渦環(huán)中心垂直誘導風速和渦環(huán)半徑作為研究參數(shù)，進行彈道仿真。

表5、表6分別給出了不同渦環(huán)半徑和中心垂直誘導風速下火箭彈的彈道特征參數(shù)，其中：無風情況下，飛行時間為105.8 s，射程為34 478 m，側偏為-9.3 m，落速為367 m/s。可以看出，和彈道無風情況下相比，彈丸的飛行時間縮短，射程和側偏均減小，落速也有所減小。由表5可以看出，隨著渦環(huán)半徑的增大，上述彈道特征參數(shù)的減小幅度相應提高，但逐漸趨于平緩。一方面是由于火箭彈在推力作用下會在很短的時間內沖過微下?lián)舯┝鞯乃接绊憛^(qū)域而繼續(xù)上升；另一方面，在風場中心垂直誘導風速不變的情況下，渦環(huán)半徑的增加會降低單位空間內的風切變強度。由表6可以看出，當微下?lián)舯┝黠L場中心垂直誘導風速增大時，風場內風切變強度增大，因而彈丸的飛行時間、射程、側偏和落速的減小幅度也相應提高。

表5 不同渦環(huán)半徑下彈道仿真結果

圖10、圖11分別為不同渦環(huán)半徑和垂直誘導風速下火箭彈高低攻角和方向攻角的變化曲線。圖中：t為彈丸飛行時間，V為微下?lián)舯┝黠L場中心垂直誘導風速，δ1和δ2分別為高低攻角和方向攻角。

由圖10、圖11可以看出，由于受到中心垂直氣流的作用，火箭彈穿越微下?lián)舯┝黠L場區(qū)域時，彈軸迅速向氣流作用方向擺動，高低攻角由正變負，與無風情況下相比，彈丸高低攻角和方向攻角的震蕩幅值增大，恢復穩(wěn)定時間增加。增大渦環(huán)半徑或中心垂直誘導風速，彈丸的攻角幅值和恢復穩(wěn)定時間均相應增加。由于微下?lián)舯┝黠L場區(qū)域相對于彈丸射向對稱，且中心氣流垂直向下，因此風場對彈丸的高低攻角的影響大于對方向攻角的影響。

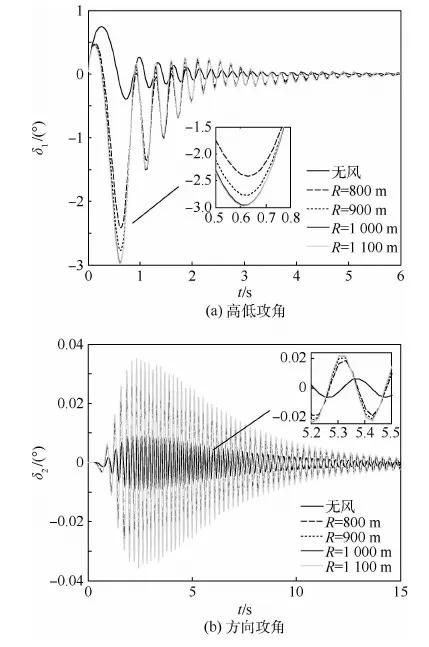
圖10 不同渦環(huán)半徑下高低攻角和方向攻角曲線Fig.10 Pitch attack angle and yaw attack angle curves with different radii of vortex ring

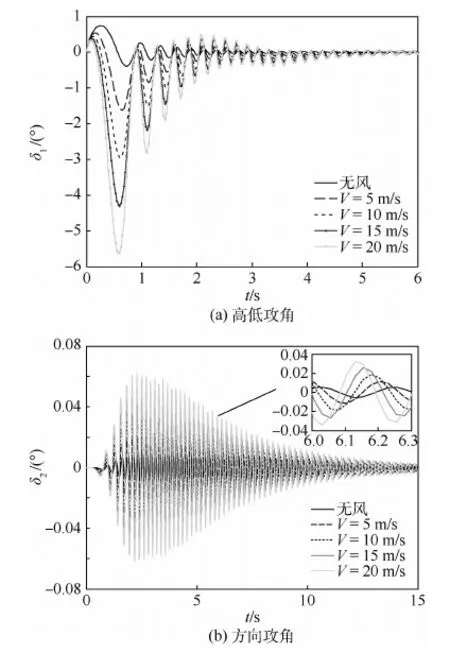
圖11 不同中心垂直誘導風速下高低攻角和方向攻角曲線Fig.11 Pitch attack angle and yaw attack angle curves with different central vertical induction wind velocities

由表5、表6和圖10、圖11可以看出，相比于微下?lián)舯┝黠L切變的尺度(渦環(huán)半徑)變化，其強度(中心垂直誘導風速)變化對火箭彈彈道特性的影響更為顯著。

3.2 低空急流對火箭彈彈道特性影響

低空急流是一種非定常流動，但考慮到火箭彈能進場或離場穿越低空急流風切變風場的時間很短，近似可按定常流動處理，基于1.2節(jié)建立的模型進行低空急流環(huán)境下的彈道仿真。

表7、表8分別給出了不同急流層最大風速和急流層頂高度下火箭彈的彈道特征參數(shù),無風情況下參數(shù)與表5、表6處一致。

由表7、表8可以看出，與無風條件下相比，低空急流風切變對火箭彈彈道產生的影響表現(xiàn)在：彈丸飛行時間縮短10 s以上，射程和側偏均減小，落速降低，其中側偏相比無風條件下增加了2.5 km以上。當急流層最大風速增大時，彈丸飛行時間、射程、側偏及落速的變化量相應增大，且上述彈道參數(shù)的變化量與急流層最大風速的增量基本線性相關；而當急流層頂高度逐漸增大時，上述彈道參數(shù)變化量雖然也隨之增大，但增幅逐漸減小，即火箭彈彈道參數(shù)的變化與急流層頂高度的變化不呈線性相關的關系。

由圖12、圖13可以看出，火箭彈穿越低空急流風切變區(qū)域時飛行姿態(tài)發(fā)生了較大改變，具體表現(xiàn)在：由于受到初始擾動，彈丸高低攻角和方向攻角幅值增大且由正變負，在穿越風場區(qū)域約2.5 s的時間內，高低攻角和方向攻角保持負值，即彈軸軸線始終低于火箭彈質心的速度矢量線，離開風切變區(qū)域后，在尾翼穩(wěn)定作用下，攻角振蕩衰減并逐漸趨于0,Us為急流層最大風速。改變低空急流風切變的風場特征參數(shù)后可以看出，急流層最大風速越大，則風切變強度越高，火箭彈攻角變化幅值越高，恢復穩(wěn)定的時間越長；急流層頂高度越高，代表低空急流風切變區(qū)域越大，但由于急流層最大風速不變，因此實際上單位空間內的風切變強度變弱，所以彈丸攻角變化幅值相應減小，攻角恢復穩(wěn)定的時間變長。

表7 不同急流層最大風速下彈道仿真結果

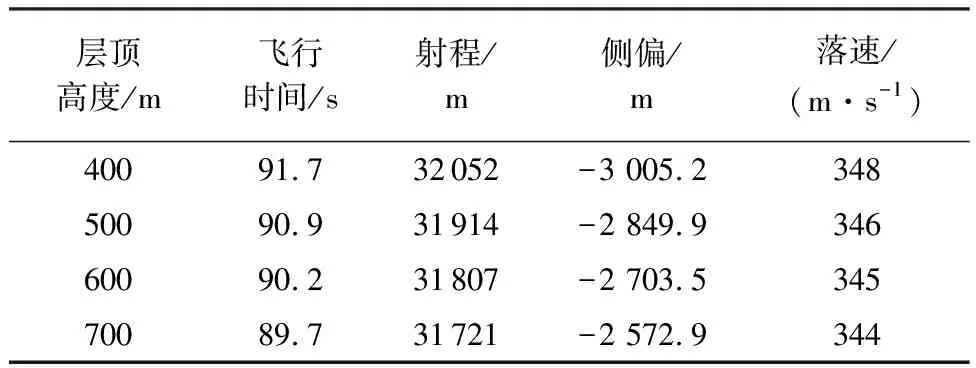
表8 不同急流層頂高度下彈道仿真結果

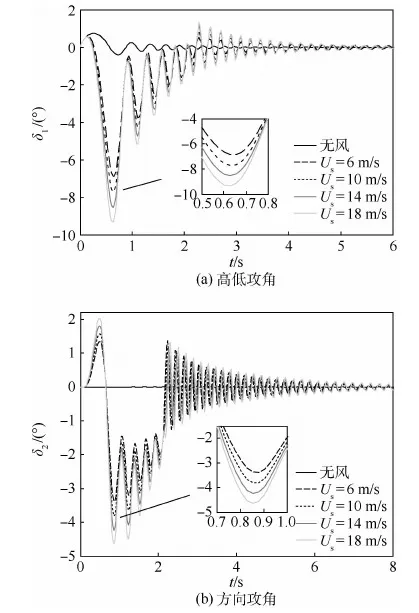
圖12 不同急流層最大風速下高低攻角和方向攻角曲線Fig.12 Pitch attack angle and yaw angle curves with different maximum wind velocities of low-level jet

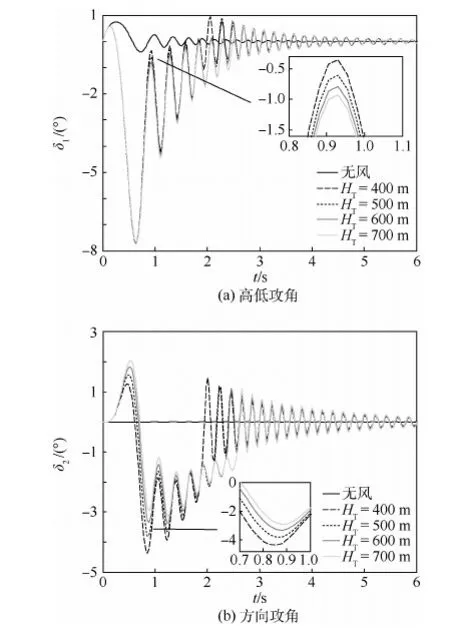
圖13 不同急流層頂高度下方向高低攻角和方向攻角曲線Fig.13 Pitch attack angle and yaw angle curves with different height of low-level jet

通過上述仿真探究可以看出，低空急流風場中，一定高度范圍內風速風向發(fā)生較大變化，相比微下?lián)舯┝黠L切變而言，低空急流風切變不僅降低了火箭彈的射程，對彈丸落點側偏也有較大的影響，且在彈丸飛行姿態(tài)方面，低空急流對彈丸攻角變化的影響要更為顯著。

4 結 論

1) 基于渦環(huán)原理的微下?lián)舯┝髂Ｐ秃突谄矫姹诿嫔淞髟淼牡涂占绷髂Ｐ途哂辛己玫娜S特性，能夠在一定程度上反應2種典型低空風切變的風場特性。

2) ①2種低空風切變均會縮短火箭彈的飛行時間，降低彈丸射程，減小彈丸落速，增大彈丸飛行過程中攻角幅值，增加攻角恢復穩(wěn)定的時間。②相對于微下?lián)舯┝鳎涂占绷鲗鸺龔椄黜棌椀捞卣鲄?shù)的影響更為明顯，尤其在彈丸的落點側偏方面，火箭彈在主動段穿越低空急流區(qū)域后側偏會發(fā)生較大變化。③增加風切變的風場強度(微下?lián)舯┝鞯闹行拇怪闭T導風速、低空急流的急流層最大風速)和空間尺度(微下?lián)舯┝鳒u環(huán)半徑、低空急流層頂高度)均會提高對火箭彈彈道特性的影響，決定風切變風場對火箭彈彈道特性影響程度的主要因素為風場強度。

當火箭彈受控時，其飛行過程中穿越風切變區(qū)域時的控制動態(tài)特性變化，以及如何對火箭彈遭遇低空風切變所形成的落點偏差進行修正，都是后續(xù)需要進一步研究的內容。

參考文獻 (References)

[1] 張冉,肖剛,徐悅.TAWS低空風切變告警功能仿真驗證平臺設計[J].電光與控制,2012,19(7):51-56.

ZHANG R，XIAO G，XU Y.A simulation and verification platform for low-level windshear warning function of TAWS[J].Electronics Optics and Control,2012,19(7):51-56(in Chinese).

[2] 王建明,潘紅華,許濤.艦載火箭炮彈道風確定探討[J].彈道學報,2004,16(1):11-15.

WANG J M,PAN H H,XU T.Research on ballistic wind of ship-borne rocket[J].Journal of Ballistics,2004,16(1):11-15(in Chinese).

[3] 吳漢洲,宋衛(wèi)東,張磊,等.低空風風場建模與對彈丸彈道特性影響的研究[J].軍械工程學院學報,2015，27(4):38-42.

WU H Z,SONG W D，ZHANG L,et al.Low-level wind model building and its influence on trajectory characteristic of projectiles[J].Journal of Ordnance Engineering College,2015，27(4):38-42(in Chinese).

[4] HUANG Z,LI X,DENG Y.The low-altitude wind shear and its influence upon hedgehopping[C]∥World Aviation Congress & Exposition.Warrendale：SAE International,2000:2000-01-5570.

[5] DIAS JR C Q,DIAS N L,FUENTES J D,et al.Convective storms and non-classical low-level jets during high ozone level episodes in the Amazon region: An ARM/GOAMAZON case study[J].Atmospheric Environment,2017,155:199-209.

[6] IVAN M.A ring-vortex downburst model for flight simulations[J].Journal of Aircraft,1986,23(3):232-236.

[7] 陶楊,韓維,吳亮.虛擬時變微下?lián)舯┝鞯臄?shù)值仿真方法[J].應用力學學報,2014，31(6):847-852.

TAO Y,HAN W,WU L.Numerical simulation method of virtual time-varying microburst[J].Chinese Journal of Applied Mechanics,2014，31(6):847-852(in Chinese).

[8] 劉時杰,徐浩軍,薛源,等.具有湍流效應的不規(guī)則微下?lián)舯┝鳂嫿ǚ椒ㄑ芯縖J].飛行力學,2014,32(4):303-307.

LIU S J,XU H J,XUE Y,et al.Construction-method of irregular microburst with turbulence effect[J].Flight Dynamics,2014,32(4):303-307(in Chinese).

[9] FIEDLER S,SCHEPANSKI K,HEINOLD B,et al.A climatology of nocturnal low-level jets over North-Africa and implications for simulating mineral dust emission[C]∥EGU General Assembly Conference,2012:4529.

[10] NUNALEE C G,BASU S.Mesoscale modeling of coastal low-level jets:Implications for offshore wind resource estimation[J].Wind Energy,2014,17(8):1199-1216.

[11] 賽瀚,苗峻峰.中國地區(qū)低空急流研究進展[J].氣象科技,2012,40(5):766-771.

SAI H,MIAO J F.Research progress of low altitude jet in China[J].Meteorological Science and Technology,2012,40(5):766-771(in Chinese).

[12] 劉鴻波,何明洋,王斌,等.低空急流的研究進展與展望[J].氣象學報,2014(2):191-206.

LIU H B,HE M Y,WANG B,et al.Advances in low-level jet research and future prospects[J].Acta Meteorologica Sinica,2014(2):191-206(in Chinese).

[13] GREENE R A.Airborne detection of low-level wind shear[J].Journal of Aircraft,1979,16(12):823-827.

[14] 谷潤平,崔鋒.飛機運行低空氣象環(huán)境仿真建模分析[J].航空計算技術,2015,45(3):1-3.

GU R P，CUI F.Modeling and simulation of low altitude meteorological environment for aircraft operations[J] Aeronautical Computing Technique,2015,45(3):1-3(in Chinese).

[15] 張冉.低空風切變下大型飛機建模、危險探測與控制律研究[D].上海：上海交通大學,2012.

ZHANG R.Research on large aircraft modeling，hazards detection and control under low-level windshear[D].Shanghai：Shanghai Jiao Tong University,2012(in Chinese).

[16] 高振興,顧宏斌.用于飛行實時仿真的微下?lián)舯┝鹘Ｑ芯縖J].系統(tǒng)仿真學報,2008,20(23):6524-6528.

GAO Z X，GU H B.Research on modeling of microburst for real time flight simulation[J].Journal of System Simulation,2008,20(23):6524-6528(in Chinese).

[17] 肖業(yè)倫,金長江.大氣擾動中的飛行原理[M].北京：國防工業(yè)出版社,1993:27-47.

XIAO Y L,JIN C J.Flight principle in atmospheric turbulence[M].Beijing： National Defense Industry Press,1993：27-47(in Chinese).

[18] 丁祖榮.工程流體力學[M].北京：機械工業(yè)出版社,2013:117-120.

DING Z R.Engineering fluid mechanics[M].Beijing：Machinery Industry Press,2013:117-120(in Chinese).

[19] 董雙林.軍用設備氣候極值 空中風速: GJB 1172.14—1991[S].北京：國防科學技術工業(yè)委員會，1991.

DONG S L.Climate extremes of military equipment:Wind speed: GJB 1172.14—1991[S].Beijing: National Defense Science and Technology Industry Committee,1991(in Chinese).

[20] ZHANG Y,SARKAR P,HU H.An experimental study of microburst-wind induced loads on a wind turbine model[C]∥AIAA Applied Aerodynamics Conference.Reston：AIAA,2013：23-42.

[21] WANKE C R,HANSMAN J R.A data fusion algorithm for multi-sensor microburst hazard assessment[C]∥AIAA Atmospheric Flight Mechanics Conference.Reston: AIAA,1992:17-29.

[22] 徐明友.火箭外彈道學[M].哈爾濱:哈爾濱工業(yè)大學出版社,2004:136-146.

XU M Y.Exterior ballistics of rockets[J].Harbin: Harbin Institute of Technology Press,2004:136-146(in Chinese).

[23] 韓子鵬.彈箭外彈道學[M].北京:北京理工大學出版社,2008:210-212.

HAN Z P.Exterior ballistics of shells and rockets[J].Beijing: Beijing University of Technology Press,2008： 210-212(in Chinese).