對一道例題的反思
張 冰
(陜西省西安交大附中 陜西西安 710048)
在高中數學實驗教材(北師大版)選修2-2《導數的幾何意義》中介紹了一道例題,課堂上講解這道題目之后,又有了很多想法和反思,現將課后對這道題目的反思記錄下來,希望對今后的教學有所啟發。
1.例:已知曲線
(1)求曲線在點處的切線方程;
(2)求曲線過點處的切線方程。
解:(1由曲線的幾何意義,曲線在點處的切線的斜率是

所以曲線在點處的切線方程為:
即:
(2)曲線過點處的切線可能(1)P是切點;(2)P不是切點
當P是切點時,即第(1)小問的情形,曲線在點處的切線方程為:
當P不是切點時,假設切點為

這時曲線的切線方程為:
通過圖像可以驗證曲線過點P的曲線確實有兩條。
課堂的例題分析、講解是結束了,在課后回顧這道例題的時候,突然想到是否對任意的一條三次曲線,過曲線上任意一點都是有兩條切線嗎?
對于三次函數過曲線上任意一點作切線,切線的情形如何?
因為以點P為切點的切線一定存在,切點不是點P的切線是否一定存在?
假設切點由點Q在曲線上,
得:
又,點Q在切線上,切線PQ的斜率

由導數的幾何意義可得:
所以,
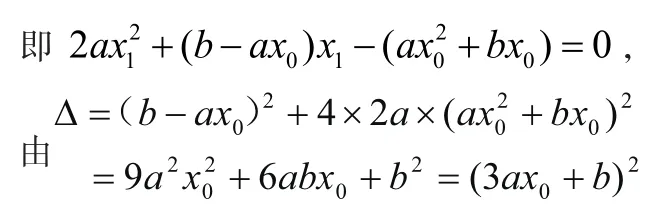
當時,點Q與點P重合,過點P有且只有一條切線;
當?≠0,即時,過點P的切線有兩條,切點分別是點P和點Q。
所以,如果,過點P的切線有且只有一條,否則有兩條切線,切點分別是點P和點Q。另一方面,正好也是的對稱軸,這樣進行判斷時就很容易了。
有什么特別的意義嗎?
我們知道是以為中心的中心對稱圖形,也是中心對稱圖形嗎?其對稱中心又是什么呢?
設函數的對稱中心為
按向量將函數的圖像平移,則所得函數是奇函數。
所以
化簡得:
上式對恒成立,有
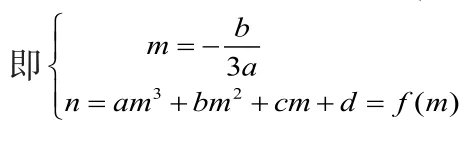
以上證明告訴我們:函數是中心對稱圖形,其對稱中心為:
,該點在其導函數:
的對稱軸上。
從對這道例題的反思中讓我更加體會到了教學的樂趣,一天的課下來,在無人的時候,翻著自己的教案,重溫課上的每一個細節,什么地方精彩,什么地方失敗,哪一句話引起了學生的共鳴,什么地方調動了學生的積極性,再對教案進行更進一步的修改,同時記錄下課上的一些突發奇想,某個靈感或突然間悟到的一種更好的調控課堂的方法,與學生溝通的方式等。時間一長,就發現自己對這些看似雞毛蒜皮的課堂細節的總結,在不知不覺中形成了自己獨特的教學風格。但細節每堂都有,總結每天進行,收獲樂趣多多。

