章節起始課學什么，怎么學？
——基于“分式”評優課的幾點思考

（江蘇省鎮江市宜城中學）

章節起始課在復習上一章的學習內容起了重要的作用，以“分式”為例，本章分為幾小節：分式、分式的基本性質、分式方程及其應用，那么，“分式”這章起始課學習什么呢？如何學習章節起始課？筆者在參加“分式”評優課過程中，對分式這章進行了分析，作了幾點思考。

一、課例分析

數學教學應從實際出發，教師根據實際提出了一系列數學活動。

問題1：兩個整數相除，計算結果一定是整數嗎？

（生）不一定，如5除以3，等等。

（師）怎么表示商？你能說出它的一種實際意義嗎？

（生）5個蘋果，3個人分，每人有5/3個。

問題2：小亮散步的速度為3km/h，走5km所用時間為 h。

變式：小亮散步的速度為3km/h，走skm所用時間為 h。

（師）兩個整式的和、差、積、商一定是整式嗎？

（生）不一定。

問題3：這樣的式子在現實中有用嗎？

（師）列式表示下列問題的數量與數量關系。

京滬鐵路是我國東部沿海地區縱貫南北的交通大動脈，全長1462km，是我國最繁忙的鐵路干線之一。如果貨車的速度是akm/h，客車的速度是貨車的2倍，那么（1）貨車從北京到上海需要多少時間？（2）客車從北京到上海需要多少時間？（3）已知從北京到上海的客車比貨車少用6h，求貨車的速度。

問題4：怎樣來定義這類新的代數式？

（師）你能舉例嗎？

（生）自由討論，得出結論。

（師）你能找出這些式子的共同特征嗎？

（生）分母中含有字母。

（師）回顧舊知（如整式，分數）找出聯系與區別。

這些式子有哪些共同特征？（從整體和局部兩個角度觀察）

（生）（1）表示兩個整式A、B相除得到的商；（2）分母中含有字母。

（師）[與整式比較]分母中含有字母（分式有意義的條件）

[與分數比較]分數是整數除以整數，分式表示兩個整式相除。

問題5：研究表格中的分式分式，它能代表某些分數嗎？

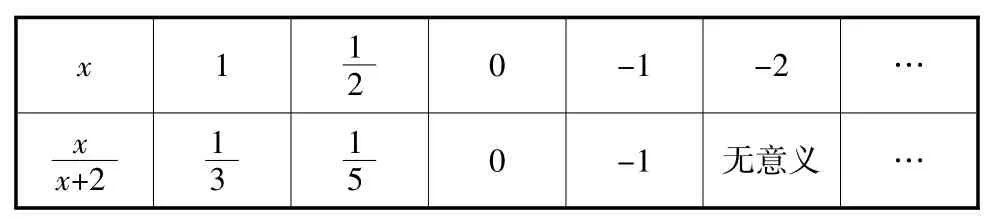
x 1 1 2 0 -1 -2 …x x+2 13 15 0 -1 無意義 …

（師）從中你能體會到分數與分式的關系嗎？

（生）分式中的字母換成數字就變成了分數，分數是分式的基礎。

二、分數與分式的聯系

分數與分式是具體與抽象、特殊與一般的關系，筆者認為這個說法體現了代數概念與代數思維的特點，為后期學習函數奠定了基礎。

“分式”這節起始課充分說明了分數的基礎，為學習分式做了類比的思想。代數概念具有符號化、形式化的特征，分式是在分數的概念基礎上進一步、更高層次的符號化、形式化，是分數概念一般化的結果，體現了分式的結構。分式具有分數的“形式”，即包含分子、分母、分數線，表示除的關系；分母中必須含有字母。

在教學中重難點就是分式的分母含有字母，字母的取值具有任意性，而不是一個固定不變的數，“分式”課例中，x取不同的值代表不同的分數，而不可忽視的是當x=-2時，分式的分母為0，此時，分式無意義，此時則需要強調分式何時有意義。

三、數學思維的重要作用

數學在培養學生的思維能力上起到了很大的作用，由于分式是在分數的基礎上進行延伸，“分式”這節課的教學用了數學中的類比思想從分數與分式的對比中進行教學，從分數的基本性質到分式的基本性質；從分數的通分、約分到分式的通分、約分；從分數的加減運算到分式的加減運算；從整式方程到分式方程，從整式方程的解到分式方程的增根。

本節課從實例出發，抽象出共同的本質屬性，類比分數歸納出分式概念，并注重一題多變。因此，類比這一數學思想方法在“分式”這節課得到了充分的體現，可以培養學生觀察概括等能力。

四、課例的設計

按照課標的要求，本節課的目標是：理解分式概念，從單元章頭出發，確定分式的概念，研究分式的基本性質，通過解決實際問題，類比分數的概念，抽象分式概念；類比分數的基本性質，總結出分式的基本概念。每一題的設計均從分數出發，讓學生充分理解分數的基本概念，分數的基本性質的概念，很快理解出分式的基本概念、基本性質，得到理想的效果。

本節課是章頭課，類比分數、整式的基本知識對分式進行研究，得出分式的基本概念、基本性質。最根本的思想是從學生已學過的分數出發，讓學生類比學習分式的概念，滲透類比的思想，不斷提升學生分析、思考問題的能力。

[1]雷正蘭.初中數學分式部分教學總結[J].科技視界，2013（19）：148.

[2]祁斌.一節“分式”復習課的點評與反思[J].中學數學教學參考旬刊，2011（1）：49-51.