基于OWA－BP神經網絡的公路隧道施工風險評估

平自要，李玉梅

（1．河南省收費還貸高速公路管理中心，河南 鄭州 450016；2．河南省交通科學技術研究院有限公司，河南 鄭州 450005；3．河南省道路材料與結構工程技術研究中心，河南 鄭州 450001）

0 引 言

隧道施工因其技術的復雜性和實施的不確定性等，成為公路工程建設過程中的高風險環節，因此隧道施工的風險評估問題顯就得尤為迫切。

在隧道及地下工程風險研究領域，美國學者Einstenin作為代表人物較早地界定了地下工程風險研究所遵循的理念及風險分析的特點［1－2］。Struk等人經過深入研究，提出了隧道及地下工程風險控制的理論框架及方法體系［3－4］。

國內針對地下工程及隧道的風險研究起步相對較晚，但隨著公路隧道、地鐵等地下工程的建設，除了逐步引進國外的風險管理理論與方法［5－6］之外，近年來國內諸多專家學者針對公路工程的風險管理問題也進行了一系列的研究，如李凡［7］從項目管理的角度對公路工程項目管理過程中的多個目標風險進行系統分析，并結合同三高速等實際工程案例進行了風險控制研究；俞素平［8］在風險分解結構RBS的基礎上對公路隧道施工風險進行了系統識別，構建了風險評估的網絡分析方法；周樹影［9］就公路工程中的高架工程風險管理問題進行了探討，提出了風險模糊評估方法并得出對應的風險應對策略；程遠等［10］運用模糊理論，從風險發生概率與風險損失相結合的角度對大跨淺埋隧道施工風險進行了評估；曹成勇等［11］針對淺埋大跨度下高速公路隧道施工風險評估問題，構建了功能系數評估方法并進行了運算。

綜合上述分析可知，現有的隧道及地下工程風險管理已經形成了相對系統的框架體系，但針對公路隧道風險評估的方法研究相對較少，且上述學者所采用的研究方法在很大程度上依賴于專家主觀經驗來確定相應指標的權重與風險程度，在具體風險評估實踐中容易失真［12－14］。因此為了提高公路隧道施工風險評估的可靠性與準確性，需要結合公路隧道施工的系統特征提出科學的風險評估新方法。本文以此為出發點，對一種基于有序加權（OWA）算子和人工神經網絡的風險評估方法進行了研究，以期為公路隧道施工風險評估提供方法支持。

1 公路隧道工程施工風險評估體系

1．1 指標體系的構建原則

對公路隧道施工風險進行綜合評估，需要以科學合理的綜合評估體系作為依托。綜合評估指標體系是風險評估的載體，是連接風險因素與評估方法模型的橋梁。由于公路隧道施工風險的影響因素繁雜且呈非線性的特點，不同類型的風險很難納入到相同層面實施分類，應以“4M1E”原理為理論依據，將公路隧道施工風險的影響指標按人員、設備、技術、材料及環境5個方面進行分類，從而涵蓋公路隧道施工現場風險管理的各個方面。同時，應深入研究《建筑施工安全風險檢查標準》（JTJ 59—2011）及相關規范和法規，結合公路隧道施工的具體工序，遵循系統性、目標性、可操作性的原則實施體系構建。

1．2 指標體系的構建

對公路隧道施工風險指標進行歸納，建立層次結構，構建涵蓋人員、機械、技術、材料、環境5個一級指標以及21個二級指標在內的風險綜合評估指標體系，如圖1所示。

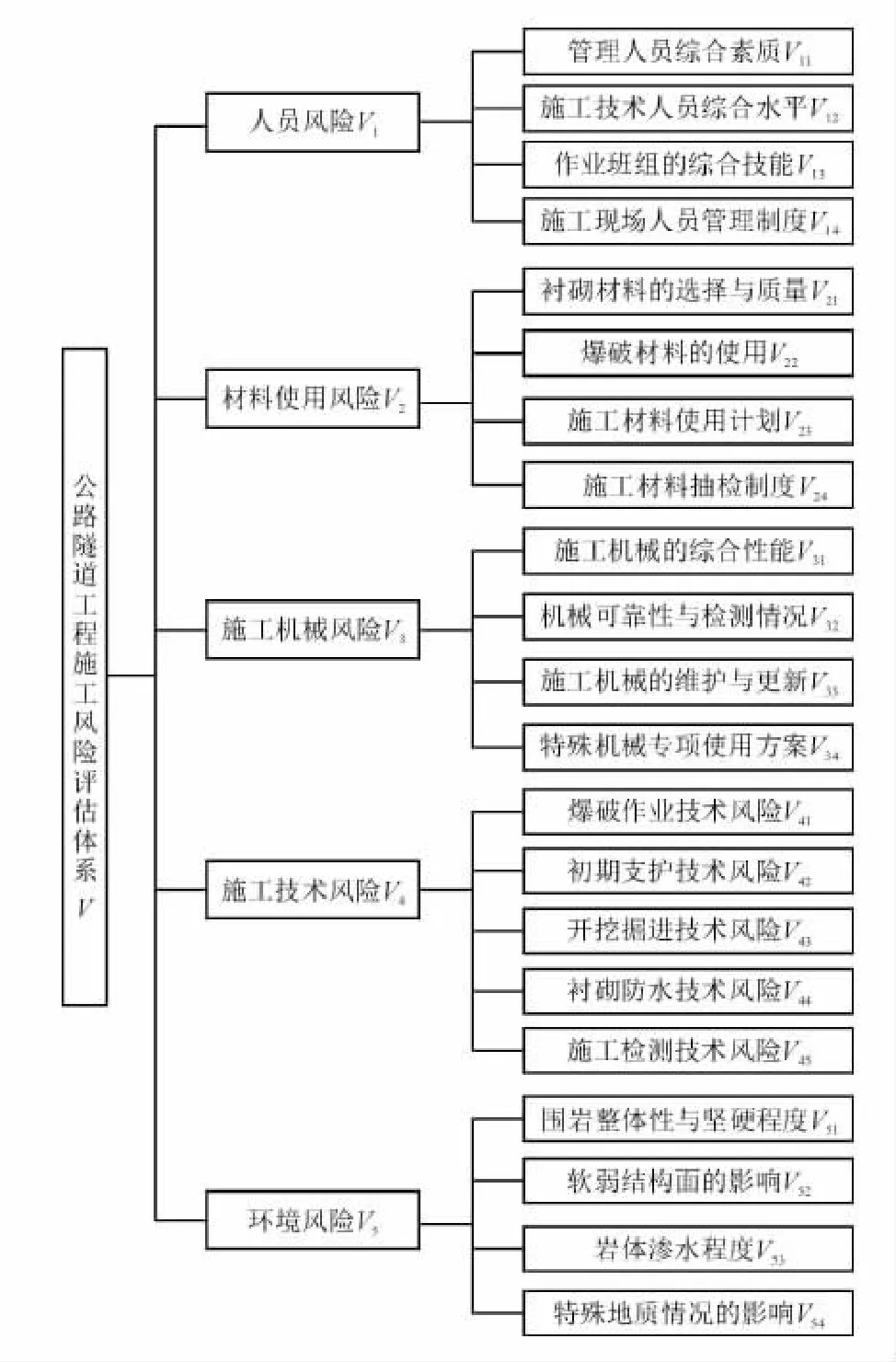
圖1 公路隧道工程施工風險綜合評估指標體系

2 基于OWA－BP神經網絡的公路隧道施工風險評估模型

2．1 評估模型的理論基礎與適用性分析

在完成指標體系構建的基礎上首先要對體系內各級指標進行權重的確定。由于公路隧道施工影響因素多且存在相互作用，使得在具體評估過程中得到的是大樣本的評估數據，在這種情況下進行權重確定就要考慮數據極端值對計算結果的影響。為了保證有限數據情況下權重確定的準確性，本文嘗試運用有序加權（OWA）算子進行賦權。OWA算子是美國學者Yager教授提出的一種客觀賦權方法。該方法通過按照一定的順序對原始數據序列重新排序、集成并根據位置先行加權處理，從而對數據實行區別對待，弱化極值的負面作用［15－16］。

公路隧道施工風險分析是一個復雜非線性關系的動態系統過程，通常需要根據多次數據變動實施反復動態評估。傳統評價方法（如模糊評估法、灰色關聯法等）難以滿足這種延展性評估的要求，當數據變動時需要重新計算分析，降低了評價的效率。為提高公路隧道施工風險評估的效率和延展性，本文嘗試運用BP神經網絡構建一種能根據數據變化及時做出調整，從而實現快速科學評估的綜合評估模型。BP神經網絡方法在模擬非線性關系、處理復雜系統多指標評價問題時，具有較好的優異性和延展性。

2．2 風險評估等級的確定

風險評估等級是實施風險評估的基礎，是風險評估分析的參照。在評估者實施評估之前，出現任何評估結果的可能性均是未知的，即出現任一風險評估結果均為等可能事件。鑒于此，在風險評估等級確定時，采用一種等分區間的測度方法。按照風險程度越高得分越低的原則界定公路隧道施工風險測度等級，測度取值區間為（0，1］，具體測度劃分如表1所示。

表1 公路隧道施工風險等級測度

2．3 OWA算子賦權

運用OWA算子進行各級指標權重的確定，具體步驟如下。

（1）設指標Vi的初始數據為（a1，a2，…，an），對初始數據按照降序的規則并從0開始重新排列，即初始數列轉化成新數列（b0，b1，…，bn），其中b0＞b1＞b2＞…＞bn。

（2）利用組合數對數據bj賦權，求得賦權向量值

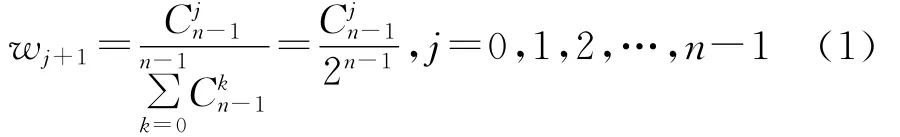
其中：Cjn－1為在n－1個數據中選擇j個數據后的組合數。

（3）利用賦權向量對決策數據加權，計算出指標Vi的絕對權重值。

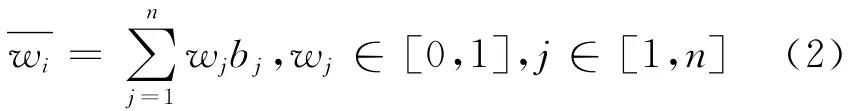
（4）求解指標Vi的相對權重值wi。

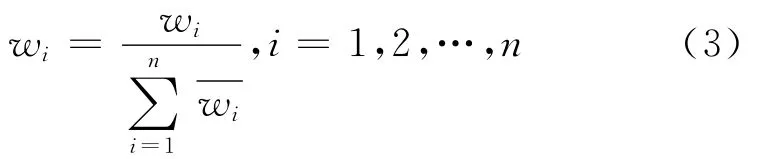
根據上述步驟，可確定指標體系內各級指標的權重。

2．4 基于BP神經網絡的風險評估

BP神經網絡通常由輸入層、隱含層、輸出層三部分構成，輸出層節點數由評估對象的實際情況確定。考慮到本文為量化研究，最終的風險評估結果為確定的數值，因此確定輸出層節點數為1，輸出值的大小表示風險等級。關于中間隱含層節點數的確定，目前尚未有明確的科學方法，故借鑒多數學者所采用的經驗公式來進行確定。即l＞log2m；l＝示隱含層、輸入層、輸出層節點數，最終構建的BP神經網絡訓練結構見圖2。

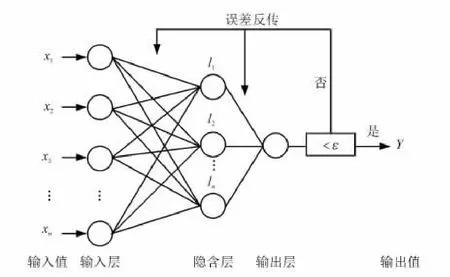
圖2 BP神經網絡訓練圖

在OWA算子確定各級指標權重的基礎上，構建下級指標層到上級指標層的網絡結構模型，設置相關訓練參數進行測試以達到網絡結構成熟。將收集的訓練樣本信息導入訓練成熟的網絡中，得到二級指標評價值，以此與指標權重進行加權計算，確定評估目標風險等級。

需要注意的是，在將數據輸入網絡結構之前，要先對其進行歸一化處理，使數據滿足統一的量綱。當同時出現正向型指標與反向型指標時，分別按公式（5）、（6）實施歸一化處理。

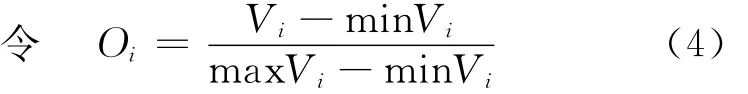
正向指標

反向指標

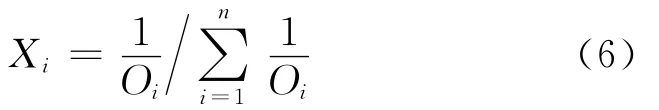
式中：Xi表示第i個輸入層的輸入值；Oi表示綜合得分值。

3 算例分析

結合三淅高速公路西坪至寺灣段某隧道施工實踐情況，運用本文構建的模型通過權重計算與評估計算實施綜合風險評估。

3．1 權重計算

6名公路隧道施工管理領域相關專家組成決策小組，對指標體系內各級指標進行重要性打分。考慮到數據處理的有效與快捷，設置打分區間為［0，10］，要求打分數據為0．5的整數倍。現以一級指標V4為例進行權重計算，打分結果見表2。

首先對指標V41的得分進行降序處理，得到新序列（8．5，8．0，8．0，8．0，7．5，7．0），根據專家組情況可知n＝6，由式（1）得出加權向量wj＝（0．031，0．156，0．313，0．313，0．156，0，031），則V41的絕對權重＝7．91。

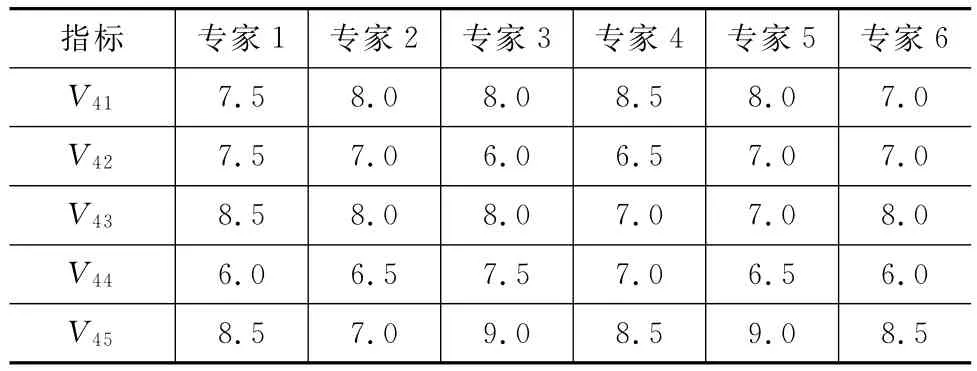
表2權重打分數據

同理可得其余指標的絕對權重：＝6．91，權重向量為

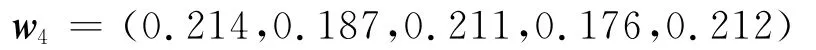
同理，各級指標權重向量為

同理可得出剩余4個一級指標的絕對權重值。

3．2 評估計算

BP神經網絡評估由Matlab自帶的神經網絡工具箱實施計算。考慮到有一級指標5個、二級指標21個，網絡結果相對復雜，輸入節點較多，應組織人數較多的綜合評估小組，按照給定的風險測度等級對各個指標進行打分評估，并采集指標相關評估數據，選擇訓練樣本40組、學習樣本3組，實施訓練直至滿意。從多次模擬的結果可知，當訓練次數滿足500次，最小訓練速率為0．8，最大允許誤差為0．001，而迭代次數為800時，模擬效果最好。模擬訓練結果如表3所示。

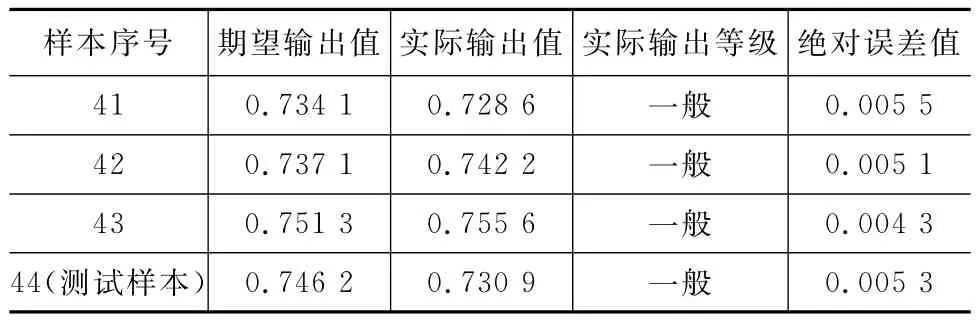
表3 基于Matlab神經網絡工具箱的訓練結果

由表3分析可知：4個樣本的期望輸出值與實際輸出值均為同一風險等級，即“一般”等級；最大誤差的絕對值為0．005 5，說明該評估模型滿足訓練精度要求。測試樣本輸出結果為0．730 9，即本項目的風險評估等級為一般，施工管理者暫時無需采取針對性的措施，應保持對施工過程的實時監測，并持續進行風險評估。隨著施工的開展，對現場評估數據實施動態監測與收集，將變動的輸入樣本導入到訓練成熟的網絡中，可實現快速科學的動態持續評估，這是該模型延展性的體現，也符合施工過程動態控制的目標。

4 結 語

（1）以“4M1E”理論為依據構建的公路隧道施工風險評估指標體系可以較為科學地反映遂道施工過程的風險指標及層次結構。

（2）運用OWA算子結合BP神經網絡構建的綜合評估模型，可以在有限數據條件下有效確定各指標的權重，滿足公路隧道施工風險評估復雜性與延展性等方面的要求。

（3）運用本研究設計的評估模型對三淅公路西坪至寺灣段某隧道施工實踐進行風險評估，結果顯示該隧道施工的風險等級為“一般”，運用本模型可以對該項目進行跟蹤風險評估。

［1］ EINSTEIN H H．Risk and Risk Analysis in Rock Engineering［J］．Tunnelling and Underground Space Technology，1996，11（2）：141－155．

［2］ EINSTEIN H H，XU S，GRASSO P，et al．Decision Aids in Tunneling［J］．World Tunneling，1998（4）：157－159．

［3］ STURK R，OLSSON L，JOHANSSON J．Risk and Decision Analysis for Large Underground Projects as Applied to the StockholmRing Road Tunneling［J］．Tunneling and Underground Space Technology，1996，11（2）：157－164．

［4］ CLARK G T，BORST A．Addressing Risk in Seattle`s Underground［J］．PB Network，2002（1）：34－37．

［5］ ESKESEN S D，TENGBORG P R，KAMPMANN J，et al．Guidelines for Tunnelling Risk Management：International Tunneling Association，Working Group No．2［J］．Tunnelling and Underground Space Technology，2008，27（4）：649－655．

［6］ 錢七虎，戎曉力．中國地下工程安全風險管理的現狀、問題及相關建議［J］．巖石力學與工程學報，2013，9（1）：216－222．

［7］ 李 凡．高速公路施工風險管理研究［D］．北京：北京交通大學，2013．

［8］ 俞素平．公路工程施工安全風險評估的網絡分析法研究［J］．地下空間與工程學報，2013，9（1）：216－222．

［9］ 周樹影．A高速公路高架工程施工風險評估與對策研究［D］．天津：天津大學，2015．

［10］ 程 遠，朱和華．基于模糊理論大跨淺埋公路隧道施工風險評估［J］．地下空間與工程學報，2016，12（6）：1616－1622．

［11］ 曹成勇，施成華．淺埋大跨下穿高速公路隧道施工風險評估及控制措施研究［J］．鐵道科學與工程學報，2016，13（7）：1440－1446．

［12］ 代春泉，王 磊．城市隧道施工風險指數法評估［J］．北京工業大學學報，2012，38（2）：251－256．

［13］ 陳結金，張永杰．下穿既有橋梁隧道施工風險定量評估方法［J］．中南大學學報：自然科學版，2015，46（5）：1862－1868．

［14］ AN Y L，PENG L M，WU B，et al．Comprehensive Extension Assessment on Tunnel Collapse Risk［J］．Journal of Central South University：Science and Technology，2011，42（2）：514－520．

［15］ YAGER R R．Families of OWA Operators［J］．FuzzySets and System，1993，59（2）：125－148．

［16］ 程 波，賈國柱．改進AHP－BP神經網絡算法研究—以建筑企業循環經濟評價為例［J］．管理評論，2015，27（1）：35－47．