基于MATLAB的連桿曲線應用與仿真
聶晶晶
(武漢商學院 機電工程與汽車服務學院,湖北 武漢 430056)
1 連桿機構
平面連桿機構是由若干桿件相互連接而組成的運動機構,連接關系有轉動副和移動副。而且平面連桿機構結構簡單,只要能設置合適尺寸、主動桿和從動桿的運動角速度就可以實現一些特定的運動軌跡需求。歷史上很早就有使用連桿機構來制造機器的記錄,并且應用非常廣泛。在很多機器和設備,儀表中都用到了連桿機構,比如縫紉機、收割機、紡織機和印刷機等等大型設備,連桿機構有四桿的、五桿的、六桿的等等,還分為平面連桿機構和空間連桿機構,平面連桿機構能夠實現的運動軌跡比較簡單,空間連桿機構能夠實現復雜的空間曲線。平面連桿機構應用這么廣泛,主要是因為其結構簡單,制造和安裝都很容易,工作比較可靠,而且成本與其他機構比較起來更加低,比較經濟。但是由于連桿機構非常靈活,設計連桿機構相對來說比較復雜,想要設計出一個連桿機構來準確的實現特定的軌跡曲線是很復雜的,而且隨著工業設計的不斷發展,工藝流程越來越復雜,連桿機構的設計也越來越復雜,尤其是想要設計出精確度高的連桿機構就更加復雜。
在1784年,科學家瓦特發明蒸汽機,在蒸汽機中他使用了連桿機構,運用四桿機構實現了接近直線的運動軌跡。隨著工業的不斷發展,計算機技術,機器人技術都在不斷發展,對于機構運動的準確性要求越來越高,對于連桿機構的研究也非常熱門。
平面連桿機構的種類很多,但是大多數連桿機構都可以由四桿機構轉化而成,因此,在平面連桿機構中,應用最廣泛的是四桿機構。由此可見,四桿機構是平面連桿機構的最簡單最基本的形式。
2 連桿曲線
在四桿機構中,桿件分為主動件和從動件。這些桿件的運動可以分為轉動,平面移動和擺動,生成的運動軌跡相應的是圓、直線或者是圓弧,橢圓弧等等。連桿上不同點的連續運動生成的運動軌跡是各種不同的軌跡曲線,這些曲線稱之為連桿曲線。連桿曲線很復雜,是高階曲線。由于有連桿機構上的點可以生成再現復雜曲線的特性,可以應用在實際的機械設計中,在工程中有非常重要的應用價值。連桿機構上的點生成的連桿曲線種類很多,可實現8字形、橢圓形、月牙形、水滴形、面包形等多種軌跡,連桿曲線的形狀與連桿機構的結構組成、桿件尺寸,初始角度,角速度及連桿上所取點的位置有關。由于連桿曲線具有靈活多變的特性,常在一切機器設備中利用連桿機構去生成特殊要求的動作軌跡。例如:攪拌機的傳動機構、摟干草機構、垂直近似平移機構、水平近似平移機構、攪面機、摟面機,汽車前窗刮雨器機構等各種各樣的機構中都是利用連桿曲線來完成不同的運動軌跡。
采用連桿機構來生成再現各種不同連桿曲線是一個有實用價值的課題。現在工業產品更新換代的速度越來越快,在設計人員按照要求設計出機械機構之后投入生產制造,這樣產品的制造精度沒有辦法得到保證。如果有一種分析方法能夠輔助設計人員進行參數的設計、機構的仿真、運動軌跡的擬合與仿真,那將大大提高生產制造的效率,并且也能提高用戶的使用感受。這對于現代工業快速的發展有很重要的意義。
3 目前常用分析方法
平面連桿設計常用的方法主要有幾何法、解析法和圖譜法。幾何法是利用機構運動過程中各連桿桿件之間的幾何關系,通過作圖來獲得連桿運動尺寸。幾何法簡單直觀,直接在圖紙上用作圖法求出各桿件的尺寸,角度以及運動,參數但由于作圖是存在誤差的,所以設計精度比較低。解析法是構件數學模型,將運動學問題轉變成數學問題,用位置、速度、加速度將問題轉化成數學方程,通過方程的求解獲得桿件尺寸,由于連桿曲線很復雜,是高階方程,所以其直觀性差,計算量大,但設計精度高。圖譜法是將可能出現的連桿曲線數據歸納采集在一個圖庫中,工程設計人員在設計連桿曲線時可以查圖譜,根據連桿曲線的類型來選擇合適的圖譜和數據。
4 連桿曲線仿真
在一些需要特定運動軌跡的場合,比如間歇運動、連續運動等,若要按照一個預先設定好的軌跡運動,則需要按照要求設計好四桿機構的尺寸,運動速度,角速度以及初始條件。在同一個四桿機構上,取不同的點得到的運動軌跡也不相同。可以采用圖譜法找到匹配的連桿曲線,但圖譜畢竟是有限的,不可能把所有不同種類、不同條件的連桿曲線都表示出來,因此利用Matlab軟件以及輔助軟件Simulink來仿真四桿機構上某一點的運動速度和運動軌跡。
利用MAT蘊AB軟件以及其附加軟件Simulink來對機構進行仿真。為了進行機構分析,機構中每一根連桿都可以表示為一個位移矢量,矢量的起點就是連桿的某一端點,而其另一端點就是矢量的終點。

圖1 連桿機構簡圖
以曲柄搖桿機構為例(如圖1所示)構建數學模型,建立矢量方程組,取四桿的桿長分別為 蘊1=40,蘊2=80,蘊3=90,蘊4=40,取一點M,構建四連桿機構閉環矢量方程,對方程求一次導得到機構運動的角速度,求二次導得到機構運動的加速度。通過標記M點的矢量位置,在MAT蘊AB軟件中編寫M文件分別描述連桿機構各桿運動方程的矩陣方程,以及點E與BC桿的相對位置(包括長度和夾角),接著,在Simulink中搭建一個模型,分別調用之間編寫的兩個M文件,最后用XY graph模塊模擬仿真M點運動軌跡(x坐標為橫坐標,y坐標為縱坐標)。在仿真過程中不斷的修改夾角,可得不同的E點所得到的連桿曲線如圖2所示。
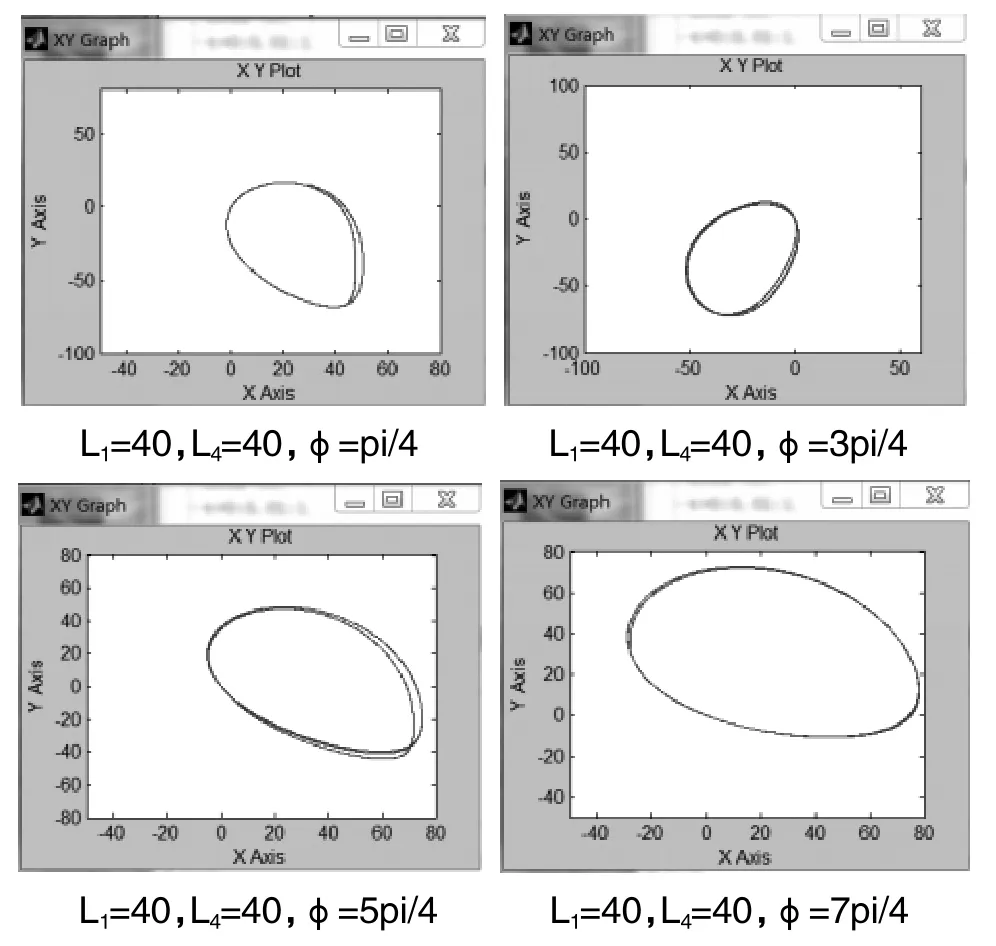
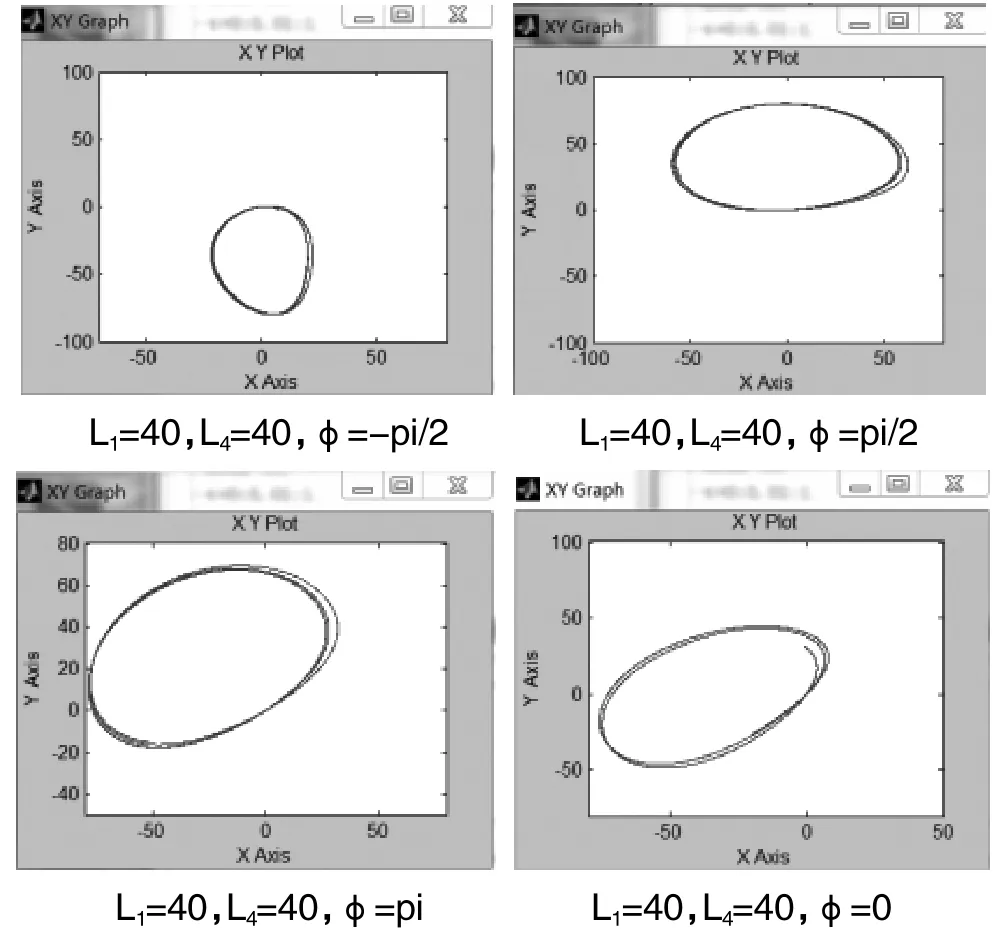
圖2 連桿曲線圖
通過仿真可以看出,在同一四桿機構中通過改變M點的角度φ,軌跡會發生相應的變化,連桿曲線的種類未變,都是長橢圓形曲線,但是曲線走向和角度發生了明顯的改變。以上仿真都是在蘊4桿長相同,但是夾角蘊4與蘊2的夾角φ不同的情況下得出的連桿曲線,可以看出即便是在同一個連桿機構上,不同的點都能形成不同的連桿曲線,根據不同的連桿曲線的需求來設計連桿機構的尺寸是非常有意義的研究。
5 結語
想要得到規定連桿曲線的連桿機構,除了采用傳統的解析法和圖譜法之外,還可以利用軟件來建立數學模型并進行仿真。通過實例研究發現,在同一個連桿機構上取不同點時所形成的連桿曲線是完全不同的,因此,工程人員想要在機械設備中設計出不同運動軌跡就有了更高效便利的方法。
[1] 于紅英,趙彥微,許棟銘.平面鉸鏈四桿機構的軌跡綜合方法[J].哈爾濱工業大學學報,2015,47(1):40-47.
[2] 吳青鳳.基于Matlab和實驗平臺的機構運動分析[J].實驗室研究與探索,2014,(8):141-143.
[3] 年大華,華志宏.連桿機構設計與應用創新[M].北京:機械工業出版社,2008.

